МНОЖЕСТВЕННАЯ РЕГРЕССИЯ Модель множественной регрессии это уравнение

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ Модель множественной регрессии – это уравнение, отражающее корреляционную связь между результатом и несколькими факторами. Общий вид: где y – зависимая переменная (результат); независимые переменные (факторы); е-случайный остаток; f-математическая функция 1

Различается модель множественной регрессии для генеральной совокупности и для выборки. В качестве функций множественной регрессии выбирают линейную, показательную и степенную: - линейная - степенная -показательная - параметры функций Из этих функций можно формировать смешанные модели, например показательную для учета влияния каких-то факторов и степенную для учета влияния других факторов. 2

При проведении корреляционно-регрессионного анализа предполагается, что наблюдения, на основе которых он проводится, были получены по однородной совокупности единиц, т. е. механизм воздействия факторов на результат должен быть примерно одинаков на разных единицах совокупности. Для обеспечения статистической достоверности модели количество наблюдений должно быть в 8 -10 раз больше количества параметров, не считая параметр, не относящийся непосредственно к какому-либо фактору ( ). 3

При построении эконометрической модели предполагается: • результат и факторы – количественные показатели; • факторы оказывают влияние на результат, • причем влияние отдельного фактора не зависит от влияния других факторов. Корреляционная связь может существовать между двумя факторами (интеркорреляция) и между несколькими факторами (мультиколлинеарность). Существование корреляционной связи между факторами может быть выявлено с помощью показателей корреляции между ними, в частности с помощью парных коэффициентов корреляции, которые записываются в виде матрицы 4

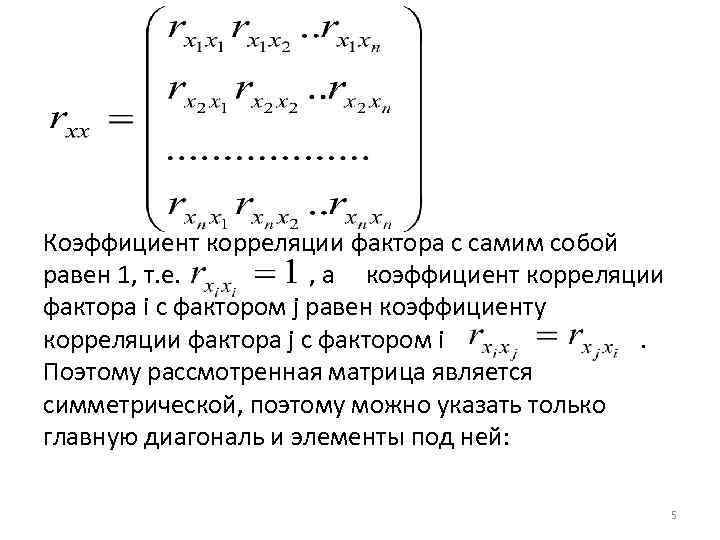Коэффициент корреляции фактора с самим собой равен 1, т. е. , а коэффициент корреляции фактора i с фактором j равен коэффициенту корреляции фактора j с фактором i . Поэтому рассмотренная матрица является симметрической, поэтому можно указать только главную диагональ и элементы под ней: 5

Наличие мультиколлинеарности можно подтвердить, если найти определитель предыдущей матрицы. Если связь между факторами полность отсутствует, то недиагональные элементы будут равны нулю, а определитель матрицы – единицы. Если связь между факторами близка к функциональной, т. е. очень тесная, то определитель матрицы будет близок к нулю. 6

Например - связь между факторами - слабая - связь между факторами слабая - связь между факторами тесная 7

Пусть - количество занятых, чел. ; - стоимость основных фондов, тыс. руб. ; - средняя заработная плата на предприятии, руб. Тогда вариация количества занятых не связана с вариацией стоимости основных фондов и вариацией средней заработной платы, в то же время, вариация стоимости основных фондов связана с вариацией средней заработной платы, причем связь прямая, т. к. коэффициент корреляции больше нуля. Это можно объяснить тем, что на более дорогом оборудовании должны работать более квалифицированные рабочие, которым выплачивается более высокая заработная плата. 8

Рассматриваем влияние факторов на результат. Рассчитываются парные коэффициенты корреляции результата с каждым из факторов: Т. е. все факторы оказывают заметное влияние на результат. Наибольшее влияние оказывает , наименьшее - , но различия в тесноте связи невелики. 9

В модель регрессии должны быть включены факторы, тесно связанные с результатом и слабо связанные друг с другом. Этим требованиям удовлетворяют две модели регрессии: Вывод о слабой связи между факторами можно сделать или рассматривая парные коэффициенты корреляции (для этих пар факторов они небольшие), но и найти определители соответствующих матриц. Например, для модели матрица парных коэффициентов межфакторной корреляции равна 10

её определитель равен 0, 87, это значение близко к 1, поэтому связь между факторами слабая. Выбор конкретной модели зависит от целей исследования. Первая модель содержит независимые переменные, которые характеризуют один и тот же фактор производства – труд. Эта модель может быть использована для решения задачи изучения влияния данного фактора на объем продукции. Вторая модель учитывает два фактора производства – труд и капитал. Область ее применения – анализ влияния на объем продукции разных факторов производства. 11