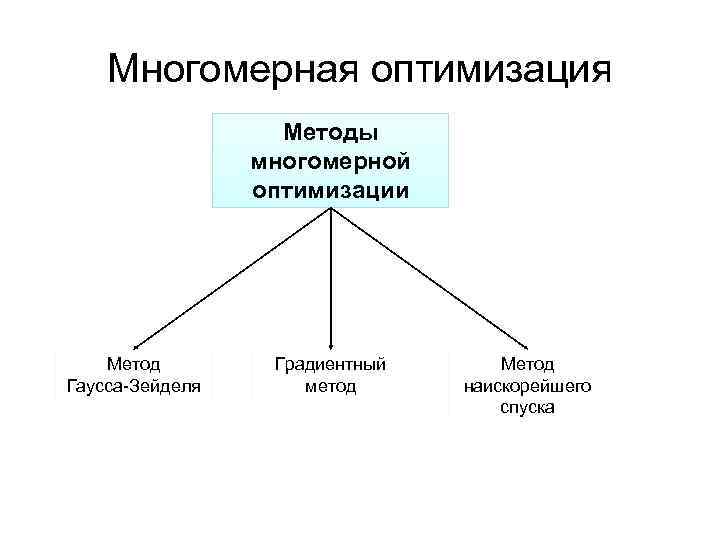
 Многомерная оптимизация Методы многомерной оптимизации Метод Градиентный Метод Гаусса-Зейделя метод наискорейшего спуска
Многомерная оптимизация Методы многомерной оптимизации Метод Градиентный Метод Гаусса-Зейделя метод наискорейшего спуска
 Методы многомерной оптимизации Для нахождения экстремума целевых функций многих переменных можно использовать различные методы, которые, в зависимости от организации поиска экстремума, делятся на две группы: • Методы, использующие собственное значение целевой функции • Методы с использованием производных
Методы многомерной оптимизации Для нахождения экстремума целевых функций многих переменных можно использовать различные методы, которые, в зависимости от организации поиска экстремума, делятся на две группы: • Методы, использующие собственное значение целевой функции • Методы с использованием производных
 Методы многомерной оптимизации В основе методов с использованием производных лежит использование итерационной процедуры
Методы многомерной оптимизации В основе методов с использованием производных лежит использование итерационной процедуры
 Метод Гаусса- Зейделя Постановка задачи Предположим, что целевая функция зависит от двух переменных: U = f(x 1, x 2). Функция имеет экстремум в виде максимума. Необходимо найти x 0 = (x 10, x 20) такие, которые определяют максимум функции Umax = f(x 10, x 20).
Метод Гаусса- Зейделя Постановка задачи Предположим, что целевая функция зависит от двух переменных: U = f(x 1, x 2). Функция имеет экстремум в виде максимума. Необходимо найти x 0 = (x 10, x 20) такие, которые определяют максимум функции Umax = f(x 10, x 20).
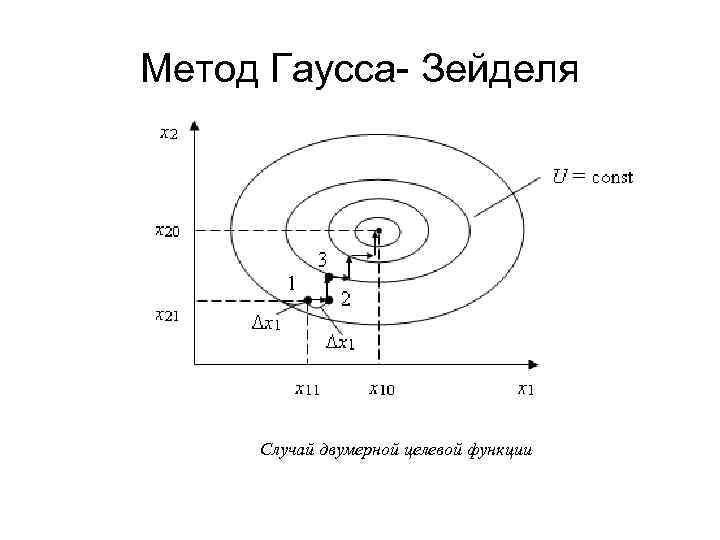 Метод Гаусса- Зейделя Случай двумерной целевой функции
Метод Гаусса- Зейделя Случай двумерной целевой функции
 Метод Гаусса- Зейделя Величина шага: В методе Гаусса-Зейделя величина шага движения регулируется в зависимости от скорости изменения функции f. При этом используется соотношение где t – параметр, определяющий величину шага. Знак производной определяет направление движения.
Метод Гаусса- Зейделя Величина шага: В методе Гаусса-Зейделя величина шага движения регулируется в зависимости от скорости изменения функции f. При этом используется соотношение где t – параметр, определяющий величину шага. Знак производной определяет направление движения.
 Метод Гаусса- Зейделя Вывод: Поиск экстремума заканчивается на шаге k, когда дважды подряд выполняется неравенство где – заданная ошибка определения экстремума
Метод Гаусса- Зейделя Вывод: Поиск экстремума заканчивается на шаге k, когда дважды подряд выполняется неравенство где – заданная ошибка определения экстремума
 Метод Гаусса- Зейделя Анализ метода: • Достоинством методов покоординатного движения и Гаусса-Зейделя является простота. • Недостаток – медленное движение к экстремуму, особенно когда количество входных переменных велико
Метод Гаусса- Зейделя Анализ метода: • Достоинством методов покоординатного движения и Гаусса-Зейделя является простота. • Недостаток – медленное движение к экстремуму, особенно когда количество входных переменных велико
 Градиентный метод оптимизации • Метод обеспечивает наискорейший подъем или спуск при движении соответственно к максимуму или минимуму. • Постановка задачи: Рассмотрим реализацию метода для целевой функции, зависимой от двух переменных: U = f(x 1, x 2). Наискорейшее движение к экстремуму обеспечивается, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения.
Градиентный метод оптимизации • Метод обеспечивает наискорейший подъем или спуск при движении соответственно к максимуму или минимуму. • Постановка задачи: Рассмотрим реализацию метода для целевой функции, зависимой от двух переменных: U = f(x 1, x 2). Наискорейшее движение к экстремуму обеспечивается, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения.
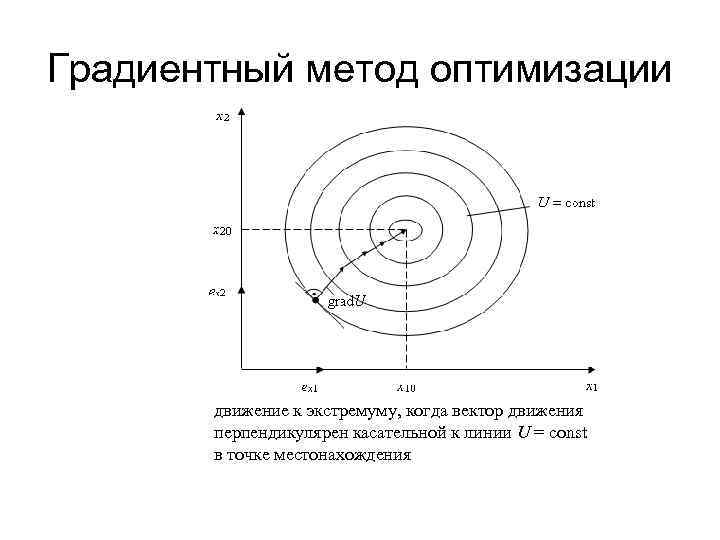 Градиентный метод оптимизации движение к экстремуму, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения
Градиентный метод оптимизации движение к экстремуму, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения
