Многогранники Виконала учениця 7 -Б класу гімназії ім

Многогранники Виконала учениця 7 -Б класу гімназії ім. Осипа Маковея Трубега Марія

Існує п’ять типів правильних опуклих многогранників: v. Тетраедр v Куб v Октаедр v Додекаедр v Ікосаедр

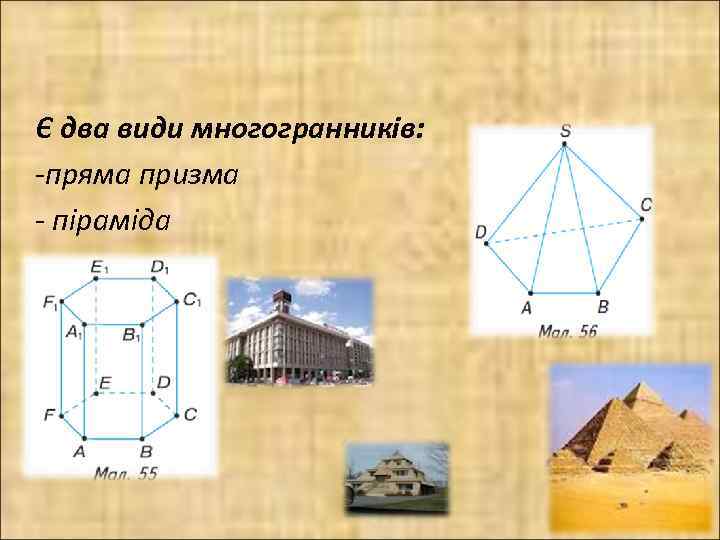
Є два види многогранників: -пряма призма - піраміда

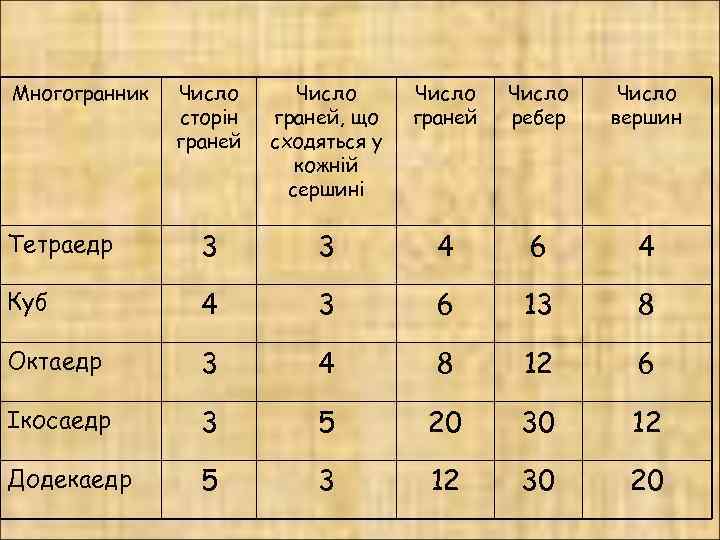
Многогранник Число сторін граней Число граней, що сходяться у кожній сершині Число граней Число ребер Число вершин Тетраедр 3 3 4 6 4 Куб 4 3 6 13 8 Октаедр 3 4 8 12 6 Ікосаедр 3 5 20 30 12 Додекаедр 5 3 12 30 20

Модель№ 1 Тетраедр називається правильним, якщо всі його 4 грані — рівносторонні трикутники У правильного тетраедра всі двогранні кути при ребрах і всі тригранні кути при вершинах рівні.

Модель№ 2 Октаедр - це багатогранник, гранями якого є 8 рівносторонніх трикутників. Так як його протилежні грані лежать в паралельних площинах.

Модель№ 3 Гексаедр (куб) Безсумнівно, куб, або, як його іноді називають математики, гексаедр – є загальновідомим і широко використовуваним багатогранником.

Модель№ 4 Ікосаедр- це двадцятигранник, . Кожна з 20 граней є рівностороннім трикут ником. Число ребер рівне 30, число вершин — 12

Модель№ 5 Додекаедр (дванадцятигранник)— об'ємна геометрична фігура, складена з дванадцяти правильних п'ятикутників. Кожна вершина додекаедра є вершиною трьох правильних п'ятикутників. Таким чином, додекаедр має 12 граней (п'ятикутних), 30 ребер і 20 вершин (у кожній сходяться 3 ребра)

Науковий внесокв розвиток теорії многогранників філософів – математиків v. Леонардо Да Вінчі v. Архімеда v. Платона v Евкліда v. Кеплера

Леонардо да Вінчі (1452 – 1519) захоплювався теорією многогранників і часто відтворював їх на своїх полотнах. Леонардо да Вінчі ввів термін " золотий перетин " , що означає такий розподіл відрізка на дві частини , коли більша його частина є середнім геометричним всього відрізка і меншою його частини.

Архімед Сіракузький Математик, фізик та інженер Архімед Сіракузький залишив після себе чимало винаходів, тринадцять творів (таких як «Про сферу й циліндрі» , «Вимірювання круга» , «Рівновага площин» , «Стомахіон» , «Правильний семикутник та інші). Архімед визначив поверхню кулі і його обсяг, вивчав «архимедову спіраль» , визначив число «пі» . Вклад Архімеда в теорію багатогранників - опис 13 напівправильних опуклих однорідних багатогранників (архімедівських тіл).

Платоновим тілами називаються правильні однорідні опуклі багатогранники , тобто опуклі багатогранники , всі грані і кути яких рівні , причому грані - правильні багатокутники. Платонова тіла - тривимірний аналог плоских правильних багатокутників. Однак між двовимірним і тривимірним випадками є важлива відмінність : існує нескінченно багато різних правильних багатокутників , але лише п'ять різних правильних багатогранників. Доказ цього факту відомо вже більше двох тисяч років ; цим доказом і вивченням п'яти правильних тіл завершуються " Початки" Евкліда. Платон

Головна праця Евкліда - «Начала» (в оригіналі « Стохейа » . «Начала » складаються з 13 книг , пізніше до них були додані ще 2. Перші шість книг присвячені планіметрії. Книги VII X містять теорію чисел , XII і XIII книги « Почав » присвячені стереометрії. Евклід представляв простір як пусте , безмежне і тривимірне. Цікаво , що « Начала» Евкліда відкриваються описом побудови правильного трикутника і закінчуються вивченням п'яти правильних багатогранних тіл! У наш час вони відомі як Платонова тіла. Евклід

Йоганн Кеплер Німецький астроном і математик. Один з творців сучасної астрономії. Вклад Кеплера в теорію багатогранника - це , по-перше , відновлення математичного змісту загубленого трактату Архімеда про напівправильних опуклих однорідних многогранниках.

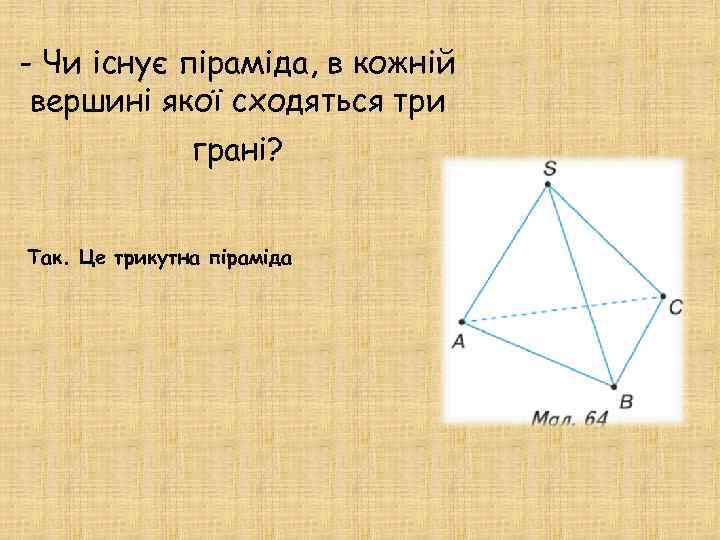
- Чи існує піраміда, в кожній вершині якої сходяться три грані? Так. Це трикутна піраміда

1. 1. Основними фігурами у стереометрії є: I. точка, площина і кут II. точка, пряма і кут III. точка, відрізок і площина IV. точка, пряма і площина. 2. Площину можна задати: I. Трьома точками, що лежать на одній прямій. II. Двома точками. III. Прямою і точкою, що не належить їй. IV. Прямою і точкою, що не належить їй. 3. Тригранний кут – це фігура складена з: I. трьох променів II. трьох трикутників III. трьох плоских кутів 4. Многогранник – це тіло складене з: I. одного многокутника II. кінцевого числа плоских кутів III. кінцевого числа плоских многокутників

5. Випуклий многогранник лежить: I. по різні сторони від площини кожного з плоских многокутників II. з однією сторони від площини кожного з плоских многокутників 6. Многокутник, складений з двох плоских многокутників, які лежать в різних площинах, і всіх відрізків, з’єднуючих точки цих многокутників, це: I. піраміда II. куб III. призма 7. Основи призми: I. перпендикулярні та рівні II. паралельні та рівні III. паралельні, але не рівні 8. Висота призми – це відстань між: I. вершинами протилежних граней II. вершинами основ III. площинами основ

9. Діагональ призми – це: I. відстань між основами II. відстань між вершинами бічної грані III. відстань між вершинами, які не належать одній грані 10. Скільки діагоналей має п’ятикутна призма: I. 5 II. 10 III. 15 11. Правильний многогранник, в якому грані – правильні трикутники і в кожній його вершині зводяться по 4 ребра: I. октаедр II. додекаедр III. ікосаедр