260606.ppt
- Количество слайдов: 139

Многогранники Работу выполнила Уч-ся 11 «А» класса МОУСО школа № 36 Глущенко Карина Учитель математики Ковальчук Л. Л. Калининград 2007

v Введение v Научный вклад в развитие теории многогранников v Выпуклые однородные многогранники. Платоновы и Архимедовы тела. v Некоторые звёздчатые формы и соединения. v Многогранники вокруг нас v Невыпуклые однородные многогранники. v Задачи «Многогранники» v Список литературы.

Тема " Многогранники " одна из основных тем в школьном курсе геометрии. Эта тема имеет яркие приложения, в том числе в живописи, архитектуре. Кроме этого в ней, по образному выражению академика А. Д. Александрова сочетаются "Лёд" и "Пламя", т. е. живое воображение и строгая логика.

Математика: лабиринты открытий. Стереометрия как наука известна уже очень давно. Изысканиями в этой области занимались многие видные умы древности. Причём издавна великие «геометры» уделяли внимание не только теоретическим положениям и практическим приложениям науки, многие понятия, образы становились незаменимыми «компонентами» их философских систем. Мы рассмотрим вклад некоторых математиков в развитие «теории многогранников» .

Научный вклад в развитие теории многогранников философовматематиков v. Леонардо Да Винчи v. Архимеда v. Платона v Евклида v. Кеплера

Золотое сечение - математический термин Леонардо да Винчи ввел термин "золотое сечение", означающий такое деление отрезка на две части, когда большая его часть является средним геометрическим всего отрезка и меньшей его части. Часто под золотым сечением понимают иррациональное число τ = 1, 6180339887498948482045868343656381177203091798. . . , равное отношению большей и меньшей частей отрезка. Иррациональное число τ было известно намного раньше. Еще Евклид использовал золотое сечение при построении правильных 5 - и 10 -угольников, а также двух правильных многогранников Платона, додекаэдра и икосаэдра 1. Золотое сечение широко применялось в геометрии и искусстве, в первую очередь в архитектуре. В 1509 г. в Венеции вышла книга Пачоли "О божественной пропорции", содержащая теорию геометрических пропорций 2. Пачоли указывает 13 свойств божественной пропорции (золотого сечения), чтобы почтить 12 апостолов и их учителя Иисуса Христа, и утверждает, что для перечисления всех свойств божественной пропорции не хватило бы чернил и бумаги. Леонардо да Винчи сделал рисунки для этого сочинения, в том числе 59 изображений многогранников.

Математик, физик и инженер Архимед Сиракузский оставил после себя немало изобретений, тринадцать сочинений (таких как «О сфере и цилиндре» , «Измерение круга» , «Равновесие плоскостей» , «Стомахион» , «Правильный семиугольник и другие). Архимед, как геометр определил поверхность шара и его объём, исследовал параболоиды и гиперболоиды, изучал «архимедову спираль» , определил число «пи» , как находящееся между 3, 141 и 3, 142. около 287 – 212 гг. до н. э. Вклад Архимеда в теорию многогранников описание 13 полуправильных выпуклых однородных многогранников (архимедовых тел).

Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники. Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. около 429 – 347 гг до н. э. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида. üХарактеристики платоновых тел
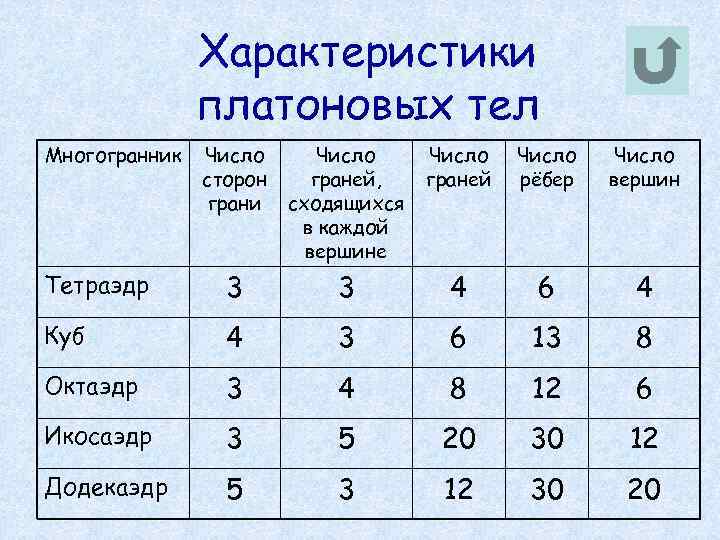
Характеристики платоновых тел Многогранник Число сторон грани Число граней, сходящихся в каждой вершине Число граней Число рёбер Число вершин Тетраэдр 3 3 4 6 4 Куб 4 3 6 13 8 Октаэдр 3 4 8 12 6 Икосаэдр 3 5 20 30 12 Додекаэдр 5 3 12 30 20

«Начала Евклида. «…в науке нет царского пути» Главный труд Евклида – «Начала» (в оригинале «Стохейа» . «Начала» состоят из 13 книг, позднее к ним были прибавлены ещё 2. Первые шесть книг посвящены планиметрии. Книги VII – X содержат теорию чисел, XII и XIII книги «Начал» посвящены стереометрии. Из постулатов Евклида видно, что он представлял пространство как пустое, безграничное, изотропное и трёхмерное. около 365 – 300 гг. до н. э. Интересно, что «Начала» Евклида открываются описанием построения правильного треугольника и заканчиваются изучением пяти правильных многогранных тел! В наше время они известны как Платоновы тела.

Немецкий астроном и математик. Один из создателей современной астрономии. Вклад Кеплера в теорию многогранника - это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра. 1571 – 1630 гг. üКосмологическая гипотеза Кеплера


Модель№ 1 Тетраэдр Простейшим среди многогранников является тетраэдр. Его четыре грани — равносторонние треугольники. Четыре — это наименьшее число граней, отделяющих часть трёхмерного пространства. Тем не менее тетраэдр обладает многими свойствами, характерными для однородных многогранников. Все его грани суть правильные многоугольники, причём каждая отделяется ребром в точности от одной грани.

Модель№ 2 Октаэдр — это многогранник, гранями которого являются восемь равносторонних треугольников. Так как его противоположные грани лежат в параллельных плоскостях

Модель№ 3 Гексаэдр (куб) Несомненно, куб, или, как его иногда называют математики, гексаэдр — самый общеизвестный и широко используемый. многогранник.

Модель№ 4 Икосаэдр — одно из пяти Платоновых тел, по простоте следующее за тетраэдром и октаэдром. Их объединяет то обстоятельство, что гранями каждого являются равносторонние треугольники.

Модель№ 5 Додекаэдр В известном смысле додекаэдр представляет наибольшую привлекательность среди Платоновых тел, соперничая с икосаэдром, который почти ему не уступает (а быть может, в чём-то и превосходит).

Модель№ 6 Усечённый тетраэдр

Модель№ 7 Усечённый октаэдр

Модель№ 8 Усечённый гексаэдр (куб) Этот многогранник представляет собой всего-навсего усечённый куб. Вряд ли его модель когонибудь особо привлечёт, но следует помнить, что это всётаки тоже однородный многогранник.

Модель№ 9 Усечённый икосаэдр

Модель№ 10 Усечённый додекаэдр Гранями этого многогранника являются правильные треугольники и десятиугольники.

Модель№ 11 Кубооктаэдр Само название многогранника указывает на некую близость его к кубу и к октаэдру. Такая близость существует в действительности. Шесть квадратных граней этого многогранника принадлежат граням некоторого куба, тогда как восемь треугольных граней принадлежат граням октаэдра.

Модель№ 12 Икосододекаэдр, подобно кубооктаэдру, являет собой квазиправильный комбинированный многогранник.

Модель№ 13 Ромбокубооктаэдр Название многогранника и на этот раз объясняет его происхождение. Множество квадратных граней ромбокубооктаэдра разбивается на два подмножества

Модель№ 14 Ромбоикосододекаэдр Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел.

Модель№ 15 Ромбоусечённый кубооктаэдр Этот многогранник, известный также под названием усечённого кубооктаэдра

Модель№ 16 Ромбоусечённый икосододекаэдр Этот многогранник часто называют также усечённым додекаэдром.

Модель№ 17 Курносый куб Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причём эти квадратные грани курносого куба окажутся как бы слегка повёрнутыми по отношению к соответственным граням куба.

Модель№ 18 Курносый додекаэдр Этот многогранник находится в таком же отношении к правильному додекаэдру, в каком курносый куб находится к правильному гексаэдру (кубу).


Модель№ 19 Звёздчатый октаэдр (stella octangula Кеплера) У октаэдра есть только одна звёздчатая форма. Её можно рассматривать как соединение двух тетраэдров.

Модель№ 20 Малый звёздчатый додекаэдр Этот многогранник — одно из тел Кеплера — Пуансо.

Модель№ 21 Большой додекаэдр Этот многогранник составлен из 12 пересекающихся пятиугольных граней.

Модель№ 22 Большой звёздчатый додекаэдр Это последняя звёздчатая форма правильного додекаэдра. модель многогранника можно изготовить, подклеивая треугольные пирамиды к граням икосаэдра.

Модель№ 23 Соединение пяти октаэдров Каждую грань этого многогранника образуют два равносторонних треугольника, расположенных так, как показано на фотографии.

Модель№ 24 Соединение пяти тетраэдров Асимметричное и скошенное положение граней этого многогранника придаёт ему необычайно привлекательный вид.

Модель№ 25 Соединение десяти тетраэдров Этот многогранник представляет собой комбинацию двух энантиоморфных форм соединения пяти тетраэдров.

Модель№ 26 Первая звёздчатая форма икосаэдра Эту модель делают из 20 частей, Каждая часть представляет собой невысокую треугольную пирамиду без основания.

Модель№ 27 Вторая звёздчатая форма икосаэдра На этой очень красивой модели заметны пятигранные высокие пики, выступающие из впадин модели соединения десяти тетраэдров.

Модель№ 28 Третья звёздчатая форма икосаэдра Этот весьма простой многогранник принадлежит к семейству дельтаэдров. Для дельтаэдров характерно, что все их грани представляют собой равносторонние треугольники

Модель№ 29 Четвёртая звёздчатая форма икосаэдра Как уже отмечалось, процесс продолжения граней икосаэдра ведёт к появлению десяти различных типов отсеков, служащих дополнением к исходному телу. Модель одной из звёздчатых форм можно построить таким образом, что отсеки, заготовки для которых показаны на рисунке внизу справа, явятся как бы связками между вершинами некоторого многогранника.

Модель№ 30 Пятая звёздчатая форма икосаэдра Многие звёздчатые формы икосаэдра внешне очень похожи на большой икосаэдр. Одна из них особенно интересна: она служит примером многогранника, вершины которого связаны только отсеками. Треугольные трафареты для этой модели совпадают с трафаретами для модели большого икосаэдра.

Модель№ 31 Шестая звёздчатая форма икосаэдра На модели легко обнаружить 12 длинных пиков, выступающих из впадин модели дельтаэдра 28.

Модель№ 32 Седьмая звёздчатая форма икосаэдра

Модель№ 33 Восьмая звёздчатая форма икосаэдра

Модель№ 34 Девятая звёздчатая форма икосаэдра На рисунке вы легко узнаете грань длинного пика модели. В предыдущих моделях пики были несколько короче, но эта состоит всего лишь из двенадцати таких пиков.

Модель№ 35 Десятая звёздчатая форма икосаэдра Дальнейшее продолжение граней икосаэдра приводит к появлению нового типа отсеков — наклонных пиков. Это единственный тип отсеков, имеющих две энантиоморфные модификации; каждая из них состоит из 60 коротких трёхгранных пирамидок

Модель№ 36 Одиннадцатая звёздчатая форма икосаэдра

Модель№ 37 Двенадцатая звёздчатая форма икосаэдра

Модель№ 38 Тринадцатая звёздчатая форма икосаэдра

Модель№ 39 Четырнадцатая звёздчатая форма икосаэдра Этот многогранник, весьма эффектный благодаря оригинальным скошенным граням, обладает обычной симметрией додекаэдра, подобно модели дельтаэдра 28, но характерен большими пятиугольными отверстиями, пронизывающими его насквозь и оставляющими как бы открытым изнутри.

Модель№ 40 Пятнадцатая звёздчатая форма икосаэдра Многогранник состоит из 60 небольших пиков, расположенных так, что нутро его остаётся пустым и видно сквозь узкие щели.

Модель№ 41 Большой икосаэдр Из описанных до сих пор многогранников, пожалуй, самым красивым и декоративным является большой икосаэдр — последний из четырёх правильных звёздчатых многогранников Кеплера — Пуансо.

Модель№ 42 Завершающая звёздчатая форма икосаэдра Показанный на фотографии многогранник — завершающая звёздчатая форма икосаэдра. Модель как бы ощетинена иглами, группирующимися по пять в красивые и отчётливо заметные гроздья. Вся модель состоит из 12 таких гроздьев.

Модель№ 43 Соединение куба и октаэдра Первой звёздчатой формой кубооктаэдра является соединение куба и октаэдра. Если воспользоваться разноцветными заготовками, то получится весьма интересная модель. Части куба можно раскрасить тремя красками, а части октаэдра — двумя другими.

Модель№ 44 Вторая звёздчатая форма кубооктаэдра Этот многогранник является следующей звёздчатой формой кубооктаэдра. Он образован из соединения куба и октаэдра добавлением 24 бипирамид.

Модель№ 45 Третья звёздчатая форма кубооктаэдра Этот многогранник весьма интересен по двум причинам. Во-первых, на его модели ясно заметно расположение квадратных граней: они группируются в пары таким образом, что грани каждой из них параллельны между собой и перпендикулярны к остальным подобным граням. Во-вторых, многогранник представляет собой своего рода соединение шести четырёхугольных пирамид, основаниями которых служат описанные выше квадраты, а боковые треугольные грани «вдавлены» в тело и касаются своими вершинами средних точек противоположных углублений.

Модель№ 46 Завершающая звёздчатая форма кубооктаэдра Итоговая звёздчатая форма кубооктаэдра особенно привлекает тем, что она является соединением двух тетраэдров, Кеплеровой stella octangula, итоговой звёздчатой формы октаэдра и трёх правильных четырёхугольных призм, общим пересечением которых является исходный куб. Каждое основание этих призм представляет собой глубокую впадину, образованную четырьмя рёбрами.

Модель№ 47 Первая звёздчатая форма икосододекаэдра Этот многогранник являет собой пример соединения двух платоновых тел — додекаэдра и икосаэдра; его можно также рассматривать как первую звёздчатую форму икосододекаэдра.

Модель№ 48 Вторая звёздчатая форма икосододекаэдра Этот многогранник — вторая звёздчатая форма икосододекаэдра, принадлежащая упомянутой выше «основной линии» . Он связан с малым звёздчатым додекаэдром и является по существу своеобразным усечённым вариантом этого правильного многогранника.

Модель№ 49 Третья звёздчатая форма икосододекаэдра Многогранник является третьей звёздчатой формой на «основной линии» икосододекаэдров. Любопытно, что одну из его граней составляет правильный пятиугольник, тогда как все остальные грани неправильные.

Модель№ 50 Четвёртая звёздчатая форма икосододекаэдра Многогранник представляет собой соединение малого звёздчатого додекаэдра и икосаэдра модели 26, которые являются первыми звёздчатыми формами додекаэдра и икосаэдра соответственно.

Модель№ 51 Пятая звёздчатая форма икосододекаэдра Многогранник устроен так: малый звёздчатый додекаэдр как бы пронизывает соединение пяти октаэдров

Модель№ 52 Шестая звёздчатая форма икосододекаэдра Звёздчатая грань этого многогранника, лежащая в одной плоскости с любой из 12 граней додекаэдра, состоит из двух правильных пентаграмм; бóльшая из них принадлежит грани малого звёздчатого додекаэдра.

Модель№ 53 Седьмая звёздчатая форма икосододекаэдра Многогранник представляет собой соединение большого додекаэдра — второй звёздчатой формы додекаэдра — и многогранника 32 — одной из звёздчатых форм икосаэдра.

Модель№ 54 Восьмая звёздчатая форма икосододекаэдра В этом многограннике легко распознать соединение пяти тетраэдров, пронизанное большим додекаэдром. Вершины последнего выглядят как маленькие розетки в центрах впадин соединения.

Модель№ 55 Девятая звёздчатая форма икосододекаэдра Многогранник представляет собой соединение 10 тетраэдров, на котором «тень» большого додекаэдра оставила следы в виде отверстий на дне впадин; из-за этого нутро многогранника становится видимым и доступным.

Модель№ 56 Десятая звёздчатая форма икосододекаэдра Этот простой многогранник внешне напоминает дельтаэдр 28 — одну из звёздчатых форм икосаэдра. Но в данном случае отверстия в центрах впадин дельтаэдра, через которые видно нутро тела, обязаны своим происхождением малому звёздчатому додекаэдру

Модель№ 57 Одиннадцатая звёздчатая форма икосододекаэдра Этот многогранник представляет особый интерес благодаря удивительному сходству с одним из однородных тел.

Модель№ 58 Двенадцатая звёздчатая форма икосододекаэдра Как можно судить по фотографии, этот многогранник весьма привлекателен. Он образован взаимопроникновением двух тел — усечённой формы большого звёздчатого додекаэдра и дельтаэдра

Модель№ 59 Тринадцатая звёздчатая форма икосододекаэдра В этой модели большой звёздчатый додекаэдр пронизан телом одного из звёздчатых икосаэдров. Поэтому 12 и 20 вершинных пиков кажутся как бы выступающими из основного ядра модели.

Модель№ 60 Четырнадцатая звёздчатая форма икосододекаэдра Этот многогранник представляет собой соединение большого звёздчатого додекаэдра с усечённой формой большого икосаэдра (усечение последнего производится путём удаления части его внешних отсеков). В результате соединения получается «колючее» тело, чем-то напоминающее морского ежа.

Модель№ 61 Соединение большого звёздчатого додекаэдра и большого икосаэдра По-видимому, самыми впечатляющими из всех многогранников следует считать правильные звёздчатые тела — большой звёздчатый додекаэдр и большой икосаэдр. Показанный на фотографии многогранник представляет собой соединение этих двух тел, являющееся одновременно звёздчатой формой икосододекаэдра.

Модель№ 62 Пятнадцатая звёздчатая форма икосододекаэдра Этот многогранник замечателен своим совершенным сходством с однородным многогранником 95, который нам ещё предстоит рассмотреть. Но в отличие от модели 95 наш многогранник не является однородным, ибо его шестиугольные звёздчатые грани отличаются от правильных, а пятиугольные — неполны, так как у них отсечены вершины. Чертежи помогут вам понять, как следовало бы видоизменить многогранник, чтобы он стал однородным.

Многогранники вокруг нас Интересно и то, что именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр. Его геометрические свойства, о которых говорилось выше, позволяют экономить генетическую информацию. Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли Na. Cl, монокристалл алюминиево-калиевых квасцов (KAl. SO 4)2 12 Н 2 О имеет форму октаэдра, кристалл сернистого колчедана Fe. S имеет форму додекаэдра, сурьмянистый сернокислый натрий - тетраэдра, бор - икосаэдра. Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.

Литография «Водопад» В центре картины расположен комплекс конструкций поднимающийся на фоне ландшафта с террасами Вертикальная ось создается двумя мощными башнями, каждая из которых увенчана остроганными многогранниками (слева - три пересекающиеся куба, а справа также три пересекающихся правильных октаэдра). Маленькие домики примыкают к башням слева и справа в едином комплексе. Слева на первом плане картины изображен маленький садик со странными, необычными подводными растениями. Центральным действием картины является ручей, который падает на колесо и крутит его. Он течет слегка полого вниз и извивается, проход я через башни, при этом он трижды протекает через точку, в которой уже проходил. Как и в конструкции Вельведера абсурдность доходит до нас через "круг" неправильных соединений куба. В результате невольного восприятия зрительная точка оказывается самой ближней, а самая высокая точка становится самой низкой. Таким образом водопад на картине осуществляет то, что мы считаем невозможным - вечное движение.


Модель№ 63 Шестнадцатая звёздчатая форма икосододекаэдра В некоторых звёздчатых икосаэдрах вершины связываются друг с другом лишь отсеками или соединениями отсеков. Благодаря этому получаются открытые, «воздушные» модели. Для построения подобных моделей подходят и отсеки, получаемые при продолжении граней икосододекаэдра.

Модель№ 64 Семнадцатая звёздчатая форма икосододекаэдра Этот многогранник тесно связан с соединением большого звёздчатого додекаэдра и большого икосаэдра (модель 61). Он может быть получен в результате удаления из тела соединения большого икосаэдра, «следы» которого остаются в виде внутренних граней многогранника. Но для того чтобы получить остающиеся отсеки большого звёздчатого додекаэдра, которые связывали бы вершины многогранника, следует закрыть ромбические грани этих отсеков.

Модель№ 65 Восемнадцатая звёздчатая форма икосододекаэдра Отверстия в теле многогранника и структура его внутренней поверхности — это следы, оставленные в большом икосаэдре после удаления большого звёздчатого додекаэдра. Десятиугольную звёздчатую грань, представляющую собой усечённую пентаграмму, которая столь заметна на приведённом чертеже, по существу на многограннике обнаружить нельзя, ибо взгляд постоянно задерживается на внешних треугольных гранях. И лишь тщательное изучение подсказывает истинное строение внутренней поверхности.

Модель№ 66 Завершающая звёздчатая форма икосододекаэдра Завершающие звёздчатые формы любых многогранников всегда вызывают особый интерес. Перед нами завершающая звёздчатая форма икосододекаэдра. Не правда ли, чем -то она напоминает вспышку фейерверка, когда из одной точки в разных направлениях разлетаются огненные звёзды и путь их ясно виден на фоне ночного неба. Но никакой фейерверк не сможет передать удивительной упорядоченности и математической точности этого многогранника, лучи которого чётко группируются в 12 заметных «короноидальных» групп.

Модель№ 67 Тетрагемигексаэдр В этом простом многограннике легко узнать огранённую форму октаэдра. Топологически он представляет собой известный односторонний гептаэдр (семигранник), гомеоморфный односторонней поверхности, носящей имя Штейнера В этом многограннике три экваториальных квадрата лежат в трёх взаимно перпендикулярных плоскостях, причём каждый квадрат имеет общие рёбра с четырьмя треугольниками.

Модель№ 68 Октагемиоктаэдр Этот многогранник представляет собой огранённый кубооктаэдр. Иногда его называют также октатетраэдром. Четыре экваториальные шестиугольные грани многогранника имеют общие рёбра с восемью треугольными гранями

Модель№ 69 Малый кубооктаэдр Этот многогранник получен в результате огранки ромбокубооктаэдра. Его квадратные грани лежат на плоскостях граней куба, восьмиугольные — на параллельных им плоскостях за квадратами, а треугольные грани совпадают с треугольными гранями ромбокубооктаэдра.

Модель№ 70 Малый битригональный икосододекаэдр Этот многогранник состоит из 12 пентаграмм на гранях додекаэдра и 20 треугольников на гранях икосаэдра. Как легко заметить, вблизи каждой вершины грани встречаются тройками в чередующемся порядке. Поэтому многогранник и называется битригональным икосододекаэдром.

Модель№ 71 Малый икосододекаэдр Гранями многогранника служат 20 треугольников, 20 шестиугольников и 12 пятиконечных звёзд, причём треугольники располагаются параллельно шестиугольникам и над ними.

Модель№ 72 Малый додекоикосододекаэдр Этот многогранник легко распознать как огранённую форму ромбоикосододекаэдра. Для его пятиугольных и десятиугольных параллельных граней подходит шестицветная додекаэдральная раска.

Модель№ 73 Додекододекаэдр Этот многогранник содержит 12 звёзд на гранях додекаэдра, а на параллельных плоскостях под звёздами находятся 12 пятиугольных граней, каждая из которых имеет общие рёбра с пятью пересекающими её звёздами.

Модель№ 74 Малый ромбододекаэдр Этот многогранник также получен из ромбоикосододекаэдра. Пятиугольные грани последнего удалены, и их место заняли неглубокие чаши, пятиугольные донца которых лежат на десятиугольных гранях тела. Удалены также треугольные грани: их заменили небольшие выемки, и грани выемок опятьтаки лежат на десятиугольных гранях тела. На прежних местах остались только квадраты.

Модель№ 75 Усечённый большой додекаэдр

Модель№ 76 Ромбододекаэдр Этот красивый, почти шарообразный многогранник, очень напоминает пляжный резиновый мяч.

Модель№ 77 Большой кубооктаэдр Этот многогранник представляет собой огранённый куб. Каждая восьмиугольная звезда лежит на гранях окружающего воображаемого куба Промежутки между лучами каждой звезды заполнены желобками и выемками, чередующимися между собой.

Модель№ 78 Кубогемиоктаэдр Этот многогранник служит примером другой огранки кубооктаэдра

Модель№ 79 Кубооктоусечённый кубооктаэдр Этот многогранник есть не что иное, как огранённый октаэдр. Двугранные желобки между лучами звёзд образованы частями шестиугольных граней.

Модель№ 80 Битригональный додекаэдр Этот многогранник особенно интересен своей тесной связью с большим звёздчатым додекаэдром. Описание этой связи достаточно сложное, но после завершения работы над моделью она станет для вас почти очевидной.

Модель№ 81 Большой битригональный додекоикосододекаэдр Показанный на фотографии многогранник относится к семейству икосододекаэдров.

Модель№ 82 Малый битригональный додекоикосододекаэдр Возможно, это один из самых замечательных многогранников, ибо, хотя он и имеет непосредственное отношение к звёздчатым додекаэдрам, его сумели найти только в текущем столетии, а первая публикация об этом появилась в 1954 году [18]. Трудно представить себе, почему он не был открыт ранее. Впрочем, и сами звёздчатые додекаэдры не были известны до Кеплера.

Модель№ 83 Икосододекаэдр Этот многогранник во многом схож с моделью 76, с той лишь разницей, что роль квадратных граней берут на себя шестиугольные. Это меняет очертания выемок и придаёт модели большую красоту, а также дополнительную жёсткость.

Модель№ 84 Икосододекоусечённый икосододекаэдр Изображённый на фотографии многогранник относится к семейству икосаэдра в том же смысле, в каком многогранник 79 входил в семейство октаэдра. Поэтому и технология изготовления его модели та же. Чтобы построить модель, надо вклеить попеременно между лучами десятиугольных звёзд (декаграмм) заранее подготовленные в соответствии с приведённой схемой раски мелкие треугольные части и двугранные желобки.

Модель№ 85 Квазиромбокубооктаэдр Этот многогранник во многом сходен с моделью 77 Восьмиугольные звёздчатые грани этой модели в нашем случае изымаются полностью, остаются только их рёбра. Вместо граней появляются глубокие выемки и впадины. Многогранник содержит два типа пересекающихся квадратных граней.

Модель№ 86 Малый ромбогексаэдр Этот многогранник представляет собой иной вариант огранки ромбокубооктаэдра, весьма напоминающий модель 69. Вообразите, что треугольные и квадратные грани модели 69 удалены, а все выемки закрыты новыми квадратами — перед вами искомый многогранник.

Модель№ 87 Большой битригональный икосододекаэдр Этот многогранник, как и многогранник 70, — битригональный икосододекаэдр, но в отличие от модели 70 пентаграммы отсутствуют. Их заменяют параллельные им пятиугольные грани, проходящие через центр тела. Внешними частями 20 треугольных граней модели являются равносторонние треугольники двух размеров, внешние части 12 пятиугольных граней — равнобедренные треугольники, углы при основании которых имеют 72° и 36°.

Модель№ 88 Большой икосододекаэдр Этот многогранник связан с моделью 81. Их отличие сводится к тому, что десятиугольные звёзды модели 81 здесь удалены, хотя их рёбра сохраняются. Добавление шестиугольных граней привело к появлению сложноогранённой поверхности на месте плоскости каждой прежней звезды. К тому же поверхность эта весьма замысловата.

Модель№ 89 Малый икосогемидодекаэдр Как и модель 91, эта модель представляет собой огранённую форму икосододекаэдра. Десятиугольные сечения проходят непосредственно через центр тела в его экваториальных плоскостях. Поверхность многогранника содержит глубокие пятигранные выемки — пирамиды «наизнанку» , вершины которых сходятся в центре тела.

Модель№ 90 Малый додекоикосаэдр Как и в случае многогранника 82, публикация об этом многограннике впервые появилась лишь в 1954 году [18]. На его поверхности мы видим огранённые звёзды, образованные пересечениями всего двух имеющихся типов граней: шестиугольников и десятиугольников.

Модель№ 91 Малый додекогемидодекаэдр Выше уже упоминались отношения, в которых находится этот многогранник к модели 89 и к икосододекаэдру. Треугольные отверстия на его поверхности закрыты выемками — трёхгранными пирамидами с вершинами в центре тела.

Модель№ 92 Квазиусечённый гексаэдр Многогранник представляет собой квазиусечённый куб. Шесть его октаграммы лежат на гранях внутреннего куба. Они имеют общие рёбра с восемью треугольными гранями, пересекающими куб.

Модель№ 93 Квазиусечённый кубооктаэдр Шесть октаграммы этого многогранника лежат на гранях правильного гексаэдра. 12 квадратных граней пересекаются по три, формируя края 8 трёхгранных впадин, глубоко проникающих в нутро тела. Боковые грани и основания впадин образованы пересечением шестиугольных граней тела. По этой причине боковые грани впадин совпадают с гранями усечённой stella octangula, а основания лежат на поверхности внутреннего правильного октаэдра.

Модель№ 94 Большой икосододекаэдр Изображённый на фотографии многогранник называется большим икосододекаэдром, поскольку 20 его треугольных и 12 звёздчатых пятиугольных граней лежат на подобных им гранях икосододекаэдра, но вместе с тем он не является звёздчатой формой икосододекаэдра.

Модель№ 95 Усеченный большой икосаэдр Многогранник представляет собой усечённый вариант большого икосаэдра 41, поэтому для построения можно воспользоваться раской последнего. В этом многограннике место треугольных граней занимают шестиугольные и метод соединения частей модель существенно не меняется.

Модель№ 96 Ромбоикосаэдр Рассматриваемый многогранник тесно связан с моделями 76 и 83. Все они содержат одно и то же множество из 30 пересекающихся скошенных квадратов, образующих экваториальные пояса. Но в данном случае шестиугольные грани занимают место пятиугольных, так что плоские звёзды становятся огранёнными. Кроме того, прямо над средними частями квадратных граней появляются неглубокие чаши, дно которых лежит на этих же гранях, а боковые грани, глубоко уходящие в тело многогранника, образованы четырьмя шестиугольными гранями.

Модель№ 97 Квазиусечённый звёздчатый додекаэдр Этот многогранник представляет собой квазиусечённую форму малого звёздчатого додекаэдра.

Модель№ 98 Квазиусечённый додекаэдр Этот многогранник находится в том же отношении к большому звёздчатому додекаэдру, что и модель 93 к звёздчатому октаэдру. В данном случае октаграммы заменены декаграммами. В отличие от 12 квадратных граней в модели 93 в нашем многограннике 30 квадратных граней, пересекающихся по три. Эти пересечения формируют края 20 трёхгранных выемок, глубоко проникающих в тело модели. Грани выемок образуются пересечением десятиугольных граней.

Модель№ 99 Большой додекоикосододекаэдр Эта модель особенно хороша в цвете благодаря легко различимым чеканным телесным звёздам, выступающим из десятиугольных звёздчатых граней. Её легко построить, придерживаясь обычной техники соединения частей. Гранями части I служат заготовки, форма которых напоминает нашивки на погонах.

Модель№ 100 Малый додекогемиикосаэдр Поверхность этого многогранника составляют 12 пентаграмм, лежащих в гранях додекаэдра, и 10 экваториальных шестиугольных граней, центры которых совпадают с центром тела. Модель связана с моделью 73, выемки которой на сей раз заменяются глубокими шестиугольными впадинами — пирамидами «наизнанку» . Эти впадины можно рассматривать как 12 вершинных частей большого икосаэдра, вывернутых наизнанку и вдавленных в тело модели.

Модель№ 101 Большой додекоикосаэдр Этот многогранник во всём подобен модели 81, за исключением того, что выемки и желобки последнего заменены здесь более глубокими девятигранными и четырёхгранными выемками.

Модель№ 102 Большой додекогемиикосаэдр Рассматриваемый многогранник представляет собой огранённый вариант додекододекаэдр. Поверхности огранённых звёзд образованы пересечением пятиугольных и шестиугольных граней, легко различимых на модели.

Модель№ 103 Большой ромбогексаэдр Этот многогранник имеет прямое отношение к модели 77, но четырёхгранные выемки и двугранные желобки многогранника 77 в нём заменены более глубокими девятигранными чашами и четырёхгранными желобками.

Модель№ 104 Квазиусечённый большой звёздчатый додекаэдр Этот многогранник представляет собой квазиусечённый вариант большого звёздчатого додекаэдра. Лучи последнего в этом случае отсекаются почти у самого их основания плоскостями треугольных граней, так что звёздчатые пятиугольные грани становятся десятиугольными. В итоге части секущих граней образуют трёхгранные выемки, сверху замыкающие усечённые пирамиды.

Модель№ 105 Квазиромбоикосододекаэдр Этот многогранник очень похож на модель 99 с той лишь разницей, что десятиугольные звёздчатые грани последней здесь заменены причудливым переплетением пересекающихся плоскостей. Благодаря такому переплетению появляется удивительно интересная структура огранки. Изготовление модели займёт около 30 часов.

Модель№ 106 Большой икосогемидодекаэдр Рассматриваемый многогранник непосредственно связан с моделью 94. И на этой модели можно увидеть пятигранные чаши или розетки модели 94, только здесь пятиугольные грани уступают место экваториальным декаграммам, части, которых образуют глубокие выемки. Гранями выемок и являются лучи декаграмм. Такая конструкция многогранника подсказывает способ построения его модели.

Модель№ 107 Большой додекогемидодекаэдр Этот многогранник сродни как модели 94, так и модели 106. Его конструкция очень проста, а полученная модель будет достаточно прочной. Прочность достигается за счёт своеобразного расположения граней многогранника: его десятиугольные звёздчатые грани лежат в экваториальных плоскостях параллельно двум противоположным пятиугольным звёздчатым граням.

Модель№ 108 Большой квазиусечённый икосододекаэдр Изображённый на фотографии многогранник состоит из очень большого числа частей, так что на модели обычных размеров некоторые из них, скажем огранённые звёзды, будут очень малы. Поэтому полной раской всех частей модели можно пренебречь; к тому же она слишком трудоёмка.

Модель№ 109 Большой ромбододекаэдр Десятиугольные грани этого многогранника совпадают с гранями модели 99, но вместо пятиугольных и треугольных граней в нём имеются только квадратные грани. Поэтому там, где на модели 99 были сдвоенные лучи звезды и розетки, у него глубокие выемки, образованные пересечением квадратных граней.

Модель№ 110 Малый курносый икосододекаэдр Это первая из моделей невыпуклых курносых многогранников, и её легче всего построить. 20 пар равносторонних треугольников рассекают грани исходного икосаэдра, образуя 20 шестиугольных звёзд. Звезды не являются правильными, как должно быть в однородном многограннике, хотя и получены пересечением правильных треугольников. 12 пентаграмм полностью окружены другим набором треугольников, включающим в себя 60 треугольников. Такая конструкция подсказывает простой способ изготовления модели.

Модель№ 111 Курносый додекододекаэдр Этот многогранник имеет 12 пятиугольных звёзд, расположенных в параллельных плоскостях над плоскостями пятиугольных граней, что очень сближает его с моделью 73. Но в данном случае пентаграммы имеют общие рёбра с 60 равносторонними треугольниками, что приводит к появлению «курносости» .

Модель№ 112 Курносый икосододекаэдр Как и в модели 111, пятиугольные звёздчатые грани этого многогранника лежат в плоскостях, параллельных плоскостям пятиугольных граней, но теперь пентаграммы повёрнуты относительно пятиугольников. Благодаря этому освобождается место ещё для 20 треугольников в дополнение к 60 треугольникам, имеющим общие с пентаграммами рёбра.

Модель№ 113 Большой вывернутый курносый икосододекаэдр Этот многогранник служит ещё одним примером курносого тела, модель которого сравнительно легко построить. Это объясняется тем, что вся конструкция образована повторением одних и тех же вершинных частей, поскольку все вершинные фигуры многогранника одинаковы. Модель изготавливают непосредственным соединением этих заранее выполняемых частей.

Модель№ 114 Вывернутый курносый додекододекаэдр У этого многогранника есть интересная особенность: лучи его пентаграмм как бы слегка подрезаны плоскостями граней пятиугольников и одного набора треугольников. В связи с этим конструкция тела вблизи его вершин значительно усложняется. Пятиугольные грани лежат в плоскостях, параллельных плоскостям пентаграмм, но на значительном от них удалении — практически рядом с экваториальной плоскостью многогранника.

Модель№ 115 Большой курносый додекоикосододекаэдр Характерной чертой этого многогранника является наличие сдвоенных пентаграмм, лежащих в одной плоскости. Нечто подобное мы обнаружим позже в модели 119. В рассматриваемой же модели мы видим специфически «курносое» чередование впадин, уже отмеченное в модели 113.

Модель№ 116 Большой курносый икосододекаэдр В этом многограннике содержатся очень маленькие элементы поверхности, которые, хотя формально и являются видимыми снаружи частями его граней, всё же настолько малы, что не отмечены на наших чертежах этих граней. Модели свойственны многие характерные черты уже рассмотренного многогранника 115: здесь вы вновь найдёте 12 пятигранных впадин и 60 многогранных вершин. Однако вместо сдвоенных пентаграмм модели 115 в этой модели лишь одна пентаграмма, пересекающая другие грани обычным икосаэдоальным способом. Сходство с предыдущей моделью подсказывает нам способ соединения частей: он будет аналогичным.

Модель№ 117 Большой вывернутый обратнокурносый икосододекаэдр Этот многогранник поистине замечателен своей сложностью. Глубокие пятигранные чаши на его поверхности перекрываются низко расположенными десятизвёздными розетками, загораживающими сужающиеся книзу грани чаши. Чаши образованы, казалось бы, совершенно невероятными гранями многогранника, которые кажутся фантастически запутанными. В многограннике пары треугольных граней пересекаются над центральными частями пентаграмм. Это пересечение порождает весьма стройные пикообразные клинья, вершины которых совпадают с вершинами пентаграмм.

Модель№ 118 Малый вывернутый обратнокурносый икосододекаэдр Этот сложный многогранник имеет одно общее свойство с рассмотренной выше моделью 110: как легко заметить из чертежей его граней, он обладает плоскостями симметрии. Однако по сравнению с моделью 110 построение этой модели сопряжено с большими трудностями

Модель№ 119 Большой биромбоикосододекаэдр Этот многогранник замечателен по нескольким причинам. Прежде всего математически он отличается от всех других известных нам однородных многогранников.

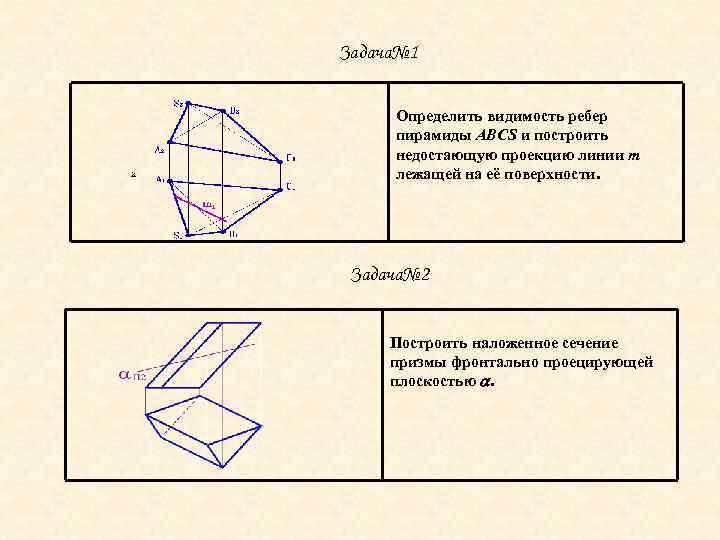
Задача№ 1 Определить видимость ребер пирамиды ABCS и построить недостающую проекцию линии m лежащей на её поверхности. Задача№ 2 Построить наложенное сечение призмы фронтально проецирующей плоскостью .
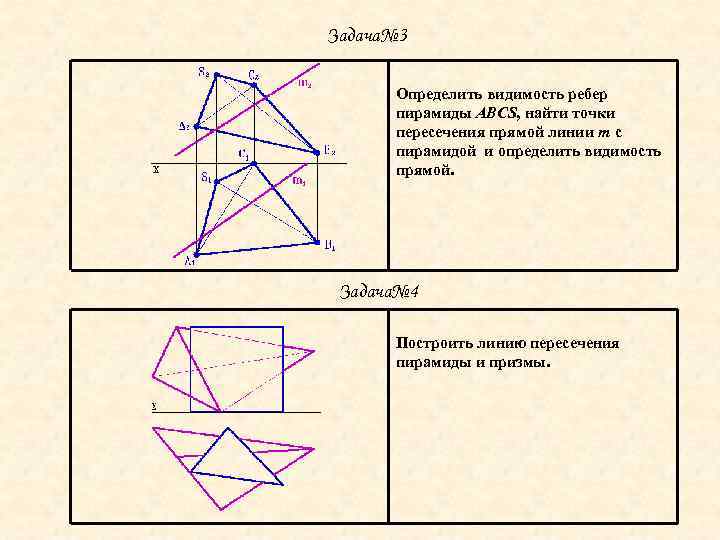
Задача№ 3 Определить видимость ребер пирамиды ABCS, найти точки пересечения прямой линии m с пирамидой и определить видимость прямой. Задача№ 4 Построить линию пересечения пирамиды и призмы.

1. Чанышев А. Н. Курс лекция по древней и средневековой философии: Учеб. Пособие для вузов. – М. : Высш. шк. , 1991. – 512 с. 2. Адамар Ж. , Элементарная геометрия, ч. 2, М. , Учпедгиз, 1958, гл. III Дополнений к ч. 2 и Прибавление F. 3. Ашкинузе В. Г. , Многоугольники и многогранники. Энциклопедия элементарной математики, кн. IV (Геометрия), М. , Физматгиз, 1963, стр. 382— 447. 4. Александров А. Д. , Выпуклые многогранники, М. —Л. , Гостехиздат, 1950.
260606.ppt