MLAB 2401 Clinical Chemistry Chapter 3 Basic Principles

MLAB 2401: Clinical Chemistry Chapter 3: Basic Principles and Practice of Clinical Chemistry, part 1 1

UNITS OF MEASURE n Measurement requires a numerical value and a unit q SI units: q length ( meter ) q mass ( gram ) q quantity ( mole ) q Volume ( liter ) q Time ( second ) n Basic units describe unrelated physical quantities n Laboratory results almost always have units of measurement associated with them 2

Unit of Measure: Prefixes n Common prefixes that are added to units of measure: n deci (d) 10 -1 n centi (c) 10 -2 n milli (m) 10 -3 n micro ( μ) 10 -6 n nano (n) 10 -9 n pico (p) 10 -12 n femto (f) 10 -15 n n Example: A common unit of liquid measurement is a deciliter( dl ), or one – tenth of a liter Combine a prefix with a basic unit results in a statement of a specific length, weight or volume q Reporting clinical chemistry results may be in units such as : n n n mg / d. L m. Eq / L 3

Conversions n Most conversions within the metric system occur in units of TEN where changing a unit of measure to a higher or lower designation requires moving the decimal one place either to the left or to the right. n When converting measures in either the high end of the scale (example kilo to mega) or the low end of the scale (examples milli to micro, micro to nano, etc. ) the decimal must be moved three places right or left as the prefix designations are assigned only to every third unit in the extreme ends. 4

Example of a conversion n How many mls are there in 2. 5 liters? The question you have to ask yourself is, what is the relationship between liters and mls? The answer : 1 liter = 1000 ml But now what? We want to get rid of the “liters’ units and end up with “mls” … Right ? 5

$1. 25 liters = _____ mls ? Remember, write a fraction that does two$

1. 25 liters = _____ mls ? Remember, write a fraction that does two things: 1. Equals 1 2. Gets rid of unwanted units and / or adds needed units 100 mg = _____ ug ? 6

n Another conversion example q q “Physiological Saline” is used in Blood Banks and Hematology to prepare Red Blood Cell suspensions. Physiological Saline is usually listed as being 0. 9 % Na. Cl 0. 9 grams of Na. Cl is added to 100 mls deionized water to make physiological saline What is the Normality (N) of physiological saline? Unwanted units cancel out leaving Eq. Wt / Liter = N Fraction = 1 Conversions are manipulations of the units – not the values !!! 7

Scientific Notation n True scientific notation format: q q 1. 22 X 104 BUT in hemo, for example a hemoglobin result would look like = 12. 2 X 103 8

Temperature n Scientific measurement of temperature is always expressed in the Celsius ( C) scale , not Fahrenheit ( F ) n Measurement of temperature is an important component of the clinical lab. Instruments, refrigerators and incubators are required to operate within specific temperatures that must be maintained and monitored. n Each laboratory must have a NIST calibrated thermometer in order to ensure the accuracy of othermometers in the laboratory n Celsius scale: 0 degrees = freezing point of water 100 degrees = boiling point of water n Conversion of Celsius to Fahrenheit and Fahrenheit to Celsius q F° = ( C ° x 1. 8 ) + 32 q C° = ( F ° - 32 ) 1. 8 9

Conversion: Temperature n Conversion of Celsius to Fahrenheit and Fahrenheit to Celsius q F° = ( C ° x 1. 8 ) + 32 q C° = ( F ° - 32 ) 1. 8 q For example: q Your refrigerator at home is probably around 40 ° F. What is that in Celsius? n Celsius= 40 -32 = 4. 4 1. 8 q Water boils at 100 ° C. What is that expressed in Fahrenheit? 10

Solutions n The clinical lab almost always uses solutions. A solution means that something has been dissolved in a liquid. In the clinical laboratory the solvent we measure most of the time is human plasma. The solute is whatever the substance is we want to measure. n Mixtures of substances – the substances in a solution are not in chemical combination with one another. n Dispersed phase - the substance is dissolved (the solute) The substance in which the solute is dissolved is the solvent. Solute + Solvent = Solution n n 11

Concentration n n Concentration – refers to the amount of one substance relative to the amounts of the other substances in the solution. Expressing Concentration q Percent solution (parts/100) n % w/w – percentage weight per weight q q n % w/v – percentage weight per volume q q n Easiest & most commonly used, very accurate if temperature controlled. Example : mg/d. L % v/v –percentage volume per volume q q n Most accurate method of expressing concentration, but can be cumbersome (especially with liquids), not often used in clinical labs. Example : mg/gm Least accurate, but used when both substances are liquids Example : m. L/L Note: volumes of liquids are not necessarily additive. 12

Solution Properties n Concentration can be measured in many different units q % Solutions: w/w, v/v , w/v (parts of solute / 100 totals parts ) Note: liquids + liquids and solids + solids alters the total parts, but solutes + solvents does not q Molarity: Moles / Liter q Molality: Moles / 1000 grams solvent 13

What is a Mole? n Mole = 6. 022 X 1023 number of atoms or molecules n Molecular Weight n n n The molecular weight( MW ) of hydrogen = 1. 0 That means that 6. 022 X 1023 hydrogen atoms weighs 1. 0 gram The MW of H 2 O = (1)(2) + (16) = 18 1 mole of water weighs 18 grams That means that 6. 022 X 1023 H 2 O molecules weigh 18. 0 grams 14

Solution Properties q Normality (normal solutions): Equivalents Weights / Liter n Working with normality, is most important when dealing with acid or bases in neutralization reactions. Equivalent Weight = MW / Valence = the electrical charge of an ion, or the number of moles that react with 1 Mole H+ 15

Equivalent Weight q Equivalent Weight = Molecular Weight / Valence n n q The valence is the electrical charge of the substance 1 Equivalent weight of any substance reacts with 1 Equivalent Weight of hydrogen ions Example n n n The MW of calcium = 40 grams Calcium ions carry a +2 electrical charge ( valence = 2 ) Equivalent Weight of calcium = 40 / 2 = 20 grams 16

Solution Properties n Normality q N = M x valence M = N / valence M is always < N q Calculation tips q q n n n Use ratio and proportion when NOT changing concentration. For calculations changing concentrations (as in titrations), use: V 1 C 1 = V 2 C 2 Important to remember that you cannot make a solution more concentrated. 17

Solution Properties n Titration – Method of measuring concentration of one solution by comparing it with a measured volume of a solution whose concentration is known n General formula: when you have a volume and concentration of one, and either the volume or the concentration of the other: V 1 C 1 = V 2 C 2 q For Example: How many mls of 1. 0 N HCl is required to prepare 25 mls of 0. 5 N HCl ? ( 1. 0 N ) ( ? mls ) = ( 0. 5 N ) ( 25 mls ) ? mls = 12. 5 mls You would need to add 12. 5 mls of 1. 0 N HCl to 12. 5 mls of deionized water ( a total volume of 25 mls ) to prepare 25 mls of 0. 5 N HCl 18

p. H and Buffers n n n n Buffers resist change in acidity Buffers are usually weak acids ( or bases) and their salts p. H is the unit used to measure acidity ( Hydrogen ion concentration ) “p” = “negative log” of the concentration of a substance in solution. Example: p. H = - log [H+] The Hydrogen ion concentration of deionized H 2 O is 1 x 10 -7 M The negative log of 10 -7 = 7. The p. H of H 2 O is 7. 0 n n The p. H scale ranges from 0 - 14 p. H 7 = neutral p. H > 7 = alkaline (basic) p. H < 7 = acid 19

Dilutions n n n A ratio of the concentrate to the total (final) volume. q A 1: 4 dilution has a 1 volume of sample and 3 volumes of diluent mixed together. Any volume can be used to create this dilution, but it must be the same unit of volume Keep in mind the sample size when making your dilution q For example: a 2: 3 dilution could contain: n n n 2 m. L serum: 1 m. L pure water 20 µL of serum: 10 µL of pure water 0. 2 m. L of serum: 0. 1 m. L of pure water 20

Dilutions n Find the dilution factor: q q q q 0. 1 m. L serum 2. 9 m. L DI water 1. 0 m. L reagent A 1. 0 m. L reagent B 5. 0 m. L total volume 0. 1 m. L serum 5. 0 m. L total =1 X X = 50 (that is the dilution factor) Dilution is 1/50 21

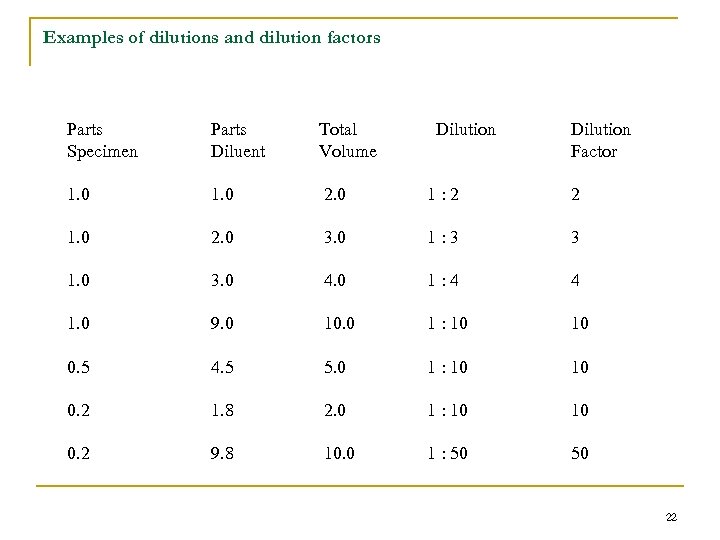
Examples of dilutions and dilution factors Parts Specimen Parts Diluent Total Volume Dilution Factor 1. 0 2. 0 1: 2 2 1. 0 2. 0 3. 0 1: 3 3 1. 0 3. 0 4. 0 1: 4 4 1. 0 9. 0 10. 0 1 : 10 10 0. 5 4. 5 5. 0 1 : 10 10 0. 2 1. 8 2. 0 1 : 10 10 0. 2 9. 8 10. 0 1 : 50 50 22

Serial Dilutions n n n In these types of questions, you are given a series of tubes. Each tube having a measured amount of a diluent. You are instructed to add a specified amount of specimen into the first tube, mix well and transfer a specified amount of the mixture to the next tube, etc. 23

Serial Dilutions n Example: q 6 tubes, each with 0. 5 m. L DI water q Add 0. 2 m. L serum to first tube and serially dilute q Find the dilution in tube # 6 n Find the dilution factor (will be the same in each of these tubes) n n 1/dil factor x 1/dil factor (etc. 6 times) Result multiplying the numerator 1 x 1 x = 1 Multiplying the denominators n Will give the result as 1 / 838 n 24

Resources n http: //www. youtube. com/watch? v=Zqd. U 3 Vf. Q _Tc 25

Solution Properties n Density – An expression in terms (usually) of a mass per unit of volume q Many examples - including specific gravity, osmolality 26

Water Specifications n Tap water is unsuitable for lab use (too many impurities) n Types of water purification techniques n n n Reagent Grades of water n n Distillation – removes most organic matter Reverse osmosis Filtration Deionization – ions removed Type I Purest – Required for sensitive tests Type II Acceptable for most uses Type III OK for washing glassware CAP - QC of water : p. H, electrical resistance, bacterial culture 27

Water filtration system for Automated chemistry analyzer. 28