Михаил Николаевич Дубовик dubovik@imp. uran. ru Рекомендуемая литература: 1. Математика: Курс лекций для технических вузов / А. Б. Соболев, А. Ф. Рыбалко. 2. Конспект лекций по высшей математике. 1 часть / Д. Т. Письменный. 3. Задачник по курсу математического анализа. Часть I / Н. Я. Виленкин и др.
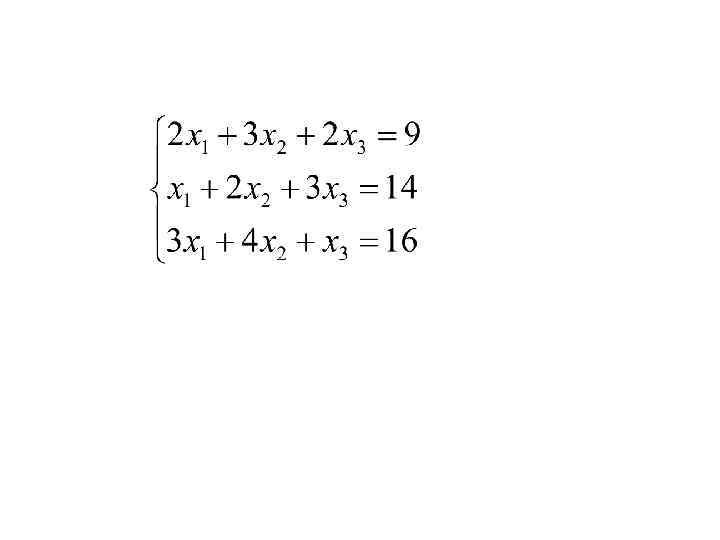
Тема 1: Матрицы и определители Если m=n, то матрица называется квадратной, а n – порядком квадратной матрицы.
Некоторые особые виды матриц:
Транспонирование – замена строк матрицы столбцами с теми же номерами.
Операции на матрицами
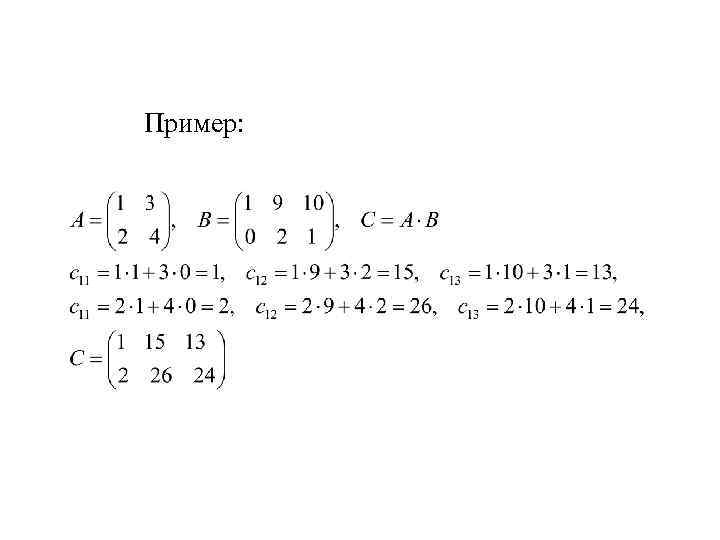
Пример:
У каждой квадратной матрицы есть определитель:
Свойства определителей:
Рассмотрим определитель порядка n.
Пример:
- разложение определителя по строке Пример: Д/з: вычислить тот же определитель по правилу Саррюса и с помощью разложения по столбцу.
Замечания: 1. Раскладывая по строке или столбцу можно вычислить определитель любого порядка. 2. Удобнее всего раскладывать по строке (столбцу) в которой (котором) больше всего нулей.
Матричные уравнения:
Пример: - матрица (3× 4) - ее миноры 2 -го и 3 -го порядка
Элементарные преобразования не меняют ранг матрицы. Матрицы, получающиеся одна из другой с помощью элементарных преобразований, называются эквивалентными.
Как определить ранг матрицы? 1. Искать не равные нулю миноры сначала 1 -го, потом 2 -го, потом 3 -го порядка и т. д. или 2. Применить метод элементарных преобразований
Скачать презентацию Михаил Николаевич Дубовик dubovik imp uran ru Рекомендуемая литература
Матрицы и определители.ppt