d46dd365d404b1c28b4499881a3a82a6.ppt
- Количество слайдов: 47

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ И. В. Миронов Иллюстративные учебные материалы к курсу лекций «Аналитическая химия» для студентов совместного Российско-Китайского института Электронно-лекционный курс разработан в рамках Программы развития НИУ-НГУ Новосибирск 2013

Аналитическая химия

Литература: 1. Кристиан Г. Аналитическая химия: в 2 томах. М. : Бином. Лаборатория знаний, 2009. 2. Золотов Ю. А. , Дорохова Е. Н. , Фадеева В. И. и др. Основы аналитической химии. М. : Высш. шк. , 2000 -2008. - Кн. 1, 2. 3. Васильев В. П. Аналитическая химия. Дрофа, 2000 -2004. Т. 1, 2. 4. Алексеев В. Н. Курс качественного химического полумикроанализа. М. : Альянс, 2008. 5. Лурье Ю. Ю. Справочник по аналитической химии. М. : Альянс, 2008. 6. Лавренова Л. Г. , Миронов И. В. , Федотова Т. Д. , Притчина Е. А. , Берус Е. И. Основы аналитической химии. Новосибирск: Новосибирский гос. ун-т, 2005. 7. Доерффель К. Статистика в аналитической химии. М. : Мир, 2000.

Разделы курса: 1. Задачи аналитической химии 2. Классификации методов анализа 3. Основные понятия аналитической химии 4. Этапы химического анализа 5. Основы метрологии -понятие -обработка данных 6. Гомогенные равновесия -влияние среды -вспомогательные функции -кислотно-основные равновесия -расчеты р. Н в различных системах -буферные системы -кислотно-основное титрование -равновесия комплексообразования

-закономерности комплексообразования -основные лиганды -маскирование -комплексометрия -комплексонометрия -окислительно-восстановительные превращения -виды окислительно-восстановительного титрования 7. Гетерогенные процессы, методы разделения. -осаждение. Влияние различных факторов на растворимость -гравиметрический метод -осадительное титрование -экстракция, ее виды -хроматография как метод разделения, идентификации и определения

Аналитическая химия – наука об определении химического состава веществ. Нередко также используется для установления химического строения. Аналитическая химия – наука о принципах и методах изучения химического состава вещества. Задачи аналитической химии как науки Развитие теории методов анализа Разработка методов анализа Развитие математического аппарата Аналитическая служба – сервисная система, обеспечивающая выполнение анализов конкретных объектов. Задачи аналитической химии как службы Анализ природных и синтетических материалов Анализ окружающей среды Контроль производства Обеспечение научно-исследовательских работ Подготовка специалистов

Аналитическая химия имеет все черты междисциплинарной науки: - обслуживает интересы других наук - использует методы: спектральные, физические, термодинамческие и др. Химический анализ – совокупность действий, направленных на получение информации о химическом составе объекта. Метод анализа – обычно универсальный и общий способ определения состава без указания на конкретный объект Методика анализа – подробное описание анализа конкретного объекта с использованием выбранного метода. Классификации: -качественный анализ -количественный анализ

Виды анализа: 1) изотопный 2) элементный 3) вещественный 4) молекулярный 5) фазовый Химический анализ — сложный многостадийный процесс. Можно выделить следующие этапы химического анализа любого объекта: постановка задачи; выбор метода и схемы анализа; отбор пробы; подготовка пробы к анализу; проведение измерения; обработка результатов измерений.
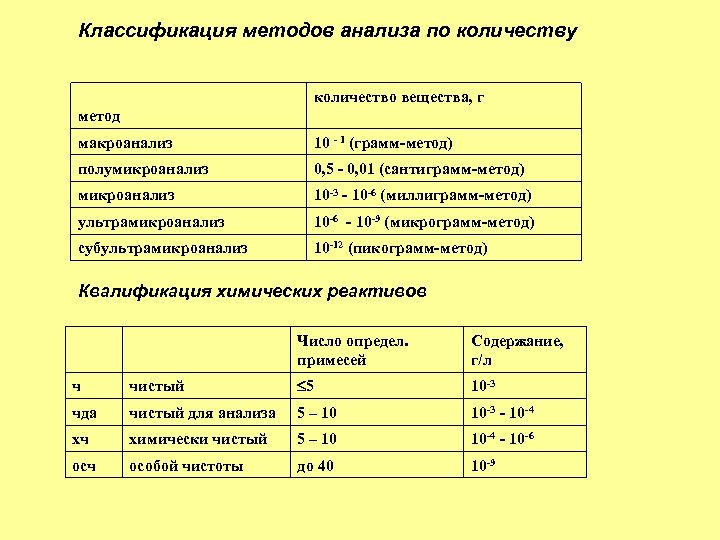
Классификация методов анализа по количеству количество вещества, г метод макроанализ 10 - 1 (грамм-метод) полумикроанализ 0, 5 - 0, 01 (сантиграмм-метод) микроанализ 10 -3 - 10 -6 (миллиграмм-метод) ультрамикроанализ 10 -6 - 10 -9 (микрограмм-метод) субультрамикроанализ 10 -12 (пикограмм-метод) Квалификация химических реактивов Число определ. примесей Содержание, г/л ч чистый 5 10 -3 чда чистый для анализа 5 – 10 10 -3 - 10 -4 хч химически чистый 5 – 10 10 -4 - 10 -6 осч особой чистоты до 40 10 -9

В наиболее употребительной систематике методы анализа подразделяются на химические, физико-химические физические методы анализа. Реже используют биологические методы анализа. К химическим методам традиционно относят грави- и титриметрию. Физико-химические и физические методы подразумевают использование приборов (спектральных, электроизмерительных, хроматографов и т. д. ), и их часто называют инструментальными.

Основные понятия аналитической химии Анализ (синтез): качественный, количественный Аналитический сигнал (!!!) Аналитическая реакция Аналитический реагент Аналитические реагенты: Групповой, Селективный Специфический Методы: Маскирование Методы разделения: Осаждение Экстракция Хроматография Дистилляция

Чувствительность метода анализа – минимальное количество вещества, которое можно определить или обнаружить данным методом. Избирательность метода – возможность определения нужных компонентов без помех со стороны других компонентов. "селективность" - ? "специфичность" возможность определять в данных условиях один компонент. Очень сильно зависит от условий – растворителя, р. Н, других компонентов. "универсальность" возможность определять или обнаруживать многие компоненты. Аналитическая реакция проводится с участием аналитического реагента. Последние подразделяются на групповые, селективные, или избирательные, и специфические. Групповым называется реагент, с помощью которого определяется целая аналитическая группа. Селективный реагент позволяет определить искомый компонент в присутствии множества других. К таким реагентам относятся, например, диметилглиоксим как реактив на никель(II) и -нитрозо- -нафтол как реактив на кобальт(II).
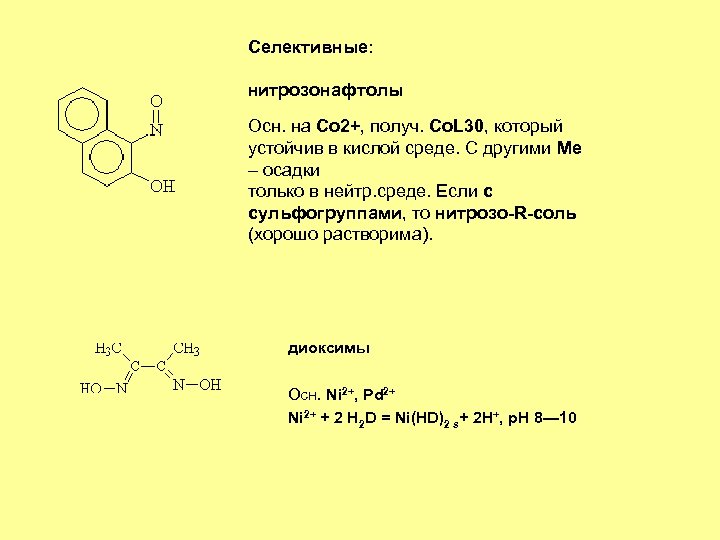
Селективные: нитрозонафтолы Осн. на Co 2+, получ. Co. L 30, который устойчив в кислой среде. С другими Ме – осадки только в нейтр. среде. Если с сульфогруппами, то нитрозо-R-соль (хорошо растворима). диоксимы Осн. Ni 2+, Pd 2+ Ni 2+ + 2 H 2 D = Ni(HD)2 s+ 2 H+, p. H 8— 10

Классификация катионов 1 группа: группового реагента нет; сульфиды растворимы – Li+, Na+, K+, Rb+, Cs+, NH 4+, Mg 2+ и др. 2 группа: групповой реагент - (NH 4)2 CO 3, сульфиды растворимы в воде – Ca 2+, Sr 2+, Ba 2+ и др. 3 группа: групповой реагент - (NH 4)2 S в нейтральной (щелочной) среде, сульфиды растворимы в разбавленных кислотах – Al 3+, Cr 3+, Fe 2+, Fe 3+, Mn 2+, Zn 2+, Co 2+, Ni 2+ и др. 4 группа: групповой реагент – H 2 S в кислой среде (HCl), сульфиды НЕ растворимы в разбавленных кислотах и (NH 4)2 Sn 1 подгруппа: Cu 2+, Cd 2+, Bi 3+, Hg 2+ и др. 2 подгруппа: As 3+, As 5+, Sb 3+, Sb 5+ и др. 5 группа: групповой реагент – HCl, сульфиды НЕ растворимы в разбавленных кислотах - Ag+, Hg 22+, Pb 2+ и др.

Основные требования к групповому реагенту 1. Количественное осаждение всех катионов данной группы 2. Получение осадка, легко растворимого в кислотах 3. Избыток реагента не должен мешать ходу анализа 4. Стоимость реагента

В анализируемой пробе часто содержатся мешающие компоненты, которые влияют на ход анализа и служат источником погрешностей. Поэтому создание методик селективного определения является актуальной задачей аналитической химии. Важные моменты: - показано, что введение в раствор какого-либо лиганда не позволяет обеспечить протекание реакции комплексообразования только с одним ионом металла, не затрагивая других. Так, изменение констант устойчивости в ряду переходных металлов таково, что не позволяет количественно разделить соседние члены ряда. Поэтому селективность обычно обеспечивается не добавлением одного реагента, а целой последовательностью процессов с участием многих реактивов. - основное значение имеет не аналитическая реакция, а аналитический сигнал. Если с каким-либо реагентом взаимодействует много компонентов, но только один из них дает окрашенное соединение, то такое определение является селективным (пример - роданид на железо(III).

- селективность зависит от условий проведения реакции. Так, осаждение диметилглиоксимата никеля(II) происходит только при определенных значениях р. Н (5 р. Н 10), в более кислой области осадок не образуется. Одним из путей повышения селективности определения компонента является маскирование (мешающих компонентов). Пример: определение Co 2+ в присутствии Fe 3+ роданидом SCN-, маскировка фторидом. . Одним из путей повышения селективности определения компонента является маскирование (мешающих компонентов). Специфичность — высшая степень селективности. Специфичных реагентов мало. К ним относят, например, крахмал как реактив на иод.

Аналитический сигнал - регистрируемое изменение свойства системы, которое связано с ее составом. Интенсивность аналитического сигнала связана с количеством определяемого компонента. Аналитическим сигналом может служить появление осадка, изменение окраски раствора, появление определенной линии в спектре, изменение ЭДС системы и т. д. Понятие аналитического сигнала связано с аналитической реакцией, она приводит к появлению аналитического сигнала. Часто аналитический сигнал – это среднее из измерений какой-то величины (физической или физико-химической), функционально связанной с содержанием определяемого компонента.

Количество вещества, концентрации В науке: Единица количества вещества - моль Количество вещества: n (молей), используется и для ионов NA = 6. 023 1023 молекул / моль Молярная масса, М Молярная масса (М) — это масса 1 моля вещества. Если известна масса вещества m, то молярную массу рассчитывают как отношение массы к числу молей n данного вещества: M = m/n. Концентрации – аналитические (общие), равновесные Шкалы: 1) молярная (molar) С = n / V: моль/л, М. Наиболее распространена, зависит от температуры 2) моляльная (molal) m = n / m (масса растворителя): моль/кг. Не зависит от температуры.

3) доли: а) мольная i = ni / nj б) массовая w = mi / mj, часто в процентах. Часто ppm (part per million) мг / л 4) массовая концентрация C = m / V (г / л, мкг / мл и т. д. ) В технологии – масса (кг, г, мкг, нг, пг), объем. Эквивалент Молярная концентрация эквивалента N, Cэк Например, N(KMn. O 4) = 5 C(KMn. O 4) для Mn. O 4– + 5 e + 8 H+ = Mn 2+ + 4 H 2 O Метрологические основы аналитической химии Метрология — это наука об измерениях, методах и средствах (широкая трактовка. Более узкая – наука об обработке данных). Точность анализа – обобщенная характеристика метода, включающая как правильность, так и воспроизводимость. Требования к точности определяются целями и задачами исследования, а также существующими объективными возможностями.

Обработка результатов анализа, случайные (random) и систематические погрешности (ошибки, errors) общ = xизм – xист – абсолютная погрешность общ = случ + сист r = общ / x – относительная погрешность случ = δ – абсолютная случайная погрешность. Обусловлена действием множества неконтролируемых факторов. Заранее неизвестна, непостоянна (даже знак). Поэтому оценивается при помощи методов математической статистики. Иногда погрешности классифицируют на инструментальные и методические. Большого смысла в этом нет. Систематическая погрешность сист – абсолютная систематическая погрешность. Обычно постоянна, либо изменяется по определенному закону. Строго говоря, не оценивается методами математической статистики, однако статистические методы иногда позволяют судить о систематической погрешности. 2 принципиальных пути: либо учитывается как добавка, либо исключается.

Выявление систематических ошибок: 1) варьирование величины пробы 2) введено-найдено 3) анализ независимым методом 4) анализ стандартных образцов и эталонов Релятивизация (погашение) – операции проводят так, чтобы погасить действие систематической погрешности (пипетки, кюветы и др. ) Рандомизация – перевод систематической ошибки в случайную ошибку (много пипеток, много термометров). Важно: в серьезных случаях никогда нельзя предполагать полное отсутствие систематических погрешностей. Можно лишь обоснованно считать, что их уровень не превышает уровень случайных погрешностей. При отсутствии значительных систематических погрешностей в этом смысле, говорят о правильности анализа (определения). Правильность как характеристика – разница между экспериментальным средним и истинным значением, т. е. характеризует систематическую ошибку.

Случайные погрешности. случ = δ = x – mx. Здесь mx – матожидание x (генеральное среднее). Строго говоря, mx = xист - сист. При отсутствии систематических погрешностей принимают, что xист = mx. Случайные ошибки имеют отношение к характеристике – прецизионность. Это степень близости друг к другу независимых результатов измерений, полученных в конкретных заданных условиях. Она зависит только от случайной погрешности и не имеет отношения к истинному значению. Мерой прецизионности является стандартное отклонение результатов — меньшая прецизионность соответствует большему стандартному отклонению. В анализе используется понятие предел обнаружения. Обычно принимают, что он соответствует 3 s фон.

Одномерные случайные величины Основные характеристики, рассчитываемые из результатов эксперимента. Важные ограничения: - речь идет только о результатах многократных измерений одной и той же величины, которая реально строго постоянна. Ошибка вносится только из-за несовершенства метода измерения. Например, это может быть концентрация компонента в одном и том же растворе. - рассматриваются только случайные погрешности. - предполагается, что распределение случайных ошибок является нормальным или близким к нему, т. е. плотность вероятности распределения ошибки имеет вид Здесь A = [(2 )1/2 ]-1, 2 – дисперсия величины δ. Матожидание m(δ) = 0, т. е. отклонения в – и в + равновероятны.

Понятия из теории вероятностей генеральная совокупность, матожидание, дисперсия, закон распределения Величина интеграла P(a) = w(δ) dδ, взятого в пределах от +a до –a равна вероятности того, что ошибка δ заключена в этих пределах. Дело в том, что большинство численных (табличных) критериев для оценок погрешностей рассчитано именно для нормально распределенных величин.

Основанием такого особого выбора нормального распределения служит центральная предельная теорема – если случайная величина является суммой большого количества случайных величин, имеющих произвольный закон распределения с ограниченными дисперсиями, то закон распределения для этой случайной величины является нормальным (асимптотически). Имеем полную аналогию со случайной погрешностью. В большинстве случаев принимается, что закон распределения случайных ошибок для исходных экспериментальных величин является близким к нормальному. Выборка - ограниченный набор случайных величин x 1, x 2, . . . , xn. Число элементов (n) — объем выборки. Рассматриваются только выборки, образованные из результатов многократных измерений одной и той же величины. Т. е. , разброс значений xi обусловлен только случайными погрешностями эксперимента. Генеральная совокупность - бесконечно большой набор случайных величин (n→ ). Выборка – случайный набор величин из этой генеральной совокупности.

Обязательно вычисляемые характеристики: 1. Среднее значение случайной величины (оценка матожидания, среднее арифметическое, выборочное среднее): используется для вычисления среднего из n равноточных результатов. "Равноточные" означает, что они имеют одинаковую дисперсию. Они определены одним и тем же методом, либо разными методами, но обеспечивающими практически одинаковую точность. Для неравноточных результатов, полученных разными методами, имеющими заметно разную ошибку, , где pi — статистический вес i результата. Вес pi учитывает неравноточность методов измерений и равен pi = A/si 2, где si 2 — дисперсия измерений данным методом, A — произвольная постоянная, одинаковая для всей выборки. В частности, можно положить A = 1.

Учет неравноточности необходим при определении одной величины разными способами. Еще раз подчеркнем, что усреднять имеет смысл только измерения одной и той же величины, например, содержание определенного компонента в данном образце. 2. Выборочная дисперсия (оценка дисперсии 2) 3. Стандартное отклонение единичного измерения (среднеквадратичное отклонение, standard deviation, SD) Это основная характеристика разброса результатов от опыта к опыту. Она зависит от выбранного метода и при неограниченном увеличении числа измерений сохраняет ненулевое значение.

Фактически характеризует воспроизводимость результатов. В аналитической химии часто применяют также относительное стандартное отклонение 4. Стандартное отклонение средней величины. . Поскольку среднее значение x получено из ограниченного числа результатов измерений (выборки), каждый из которых имеет погрешность, то оно тоже не является точным, т. е. содержит погрешность. Величина s x служит мерой этой неопределенности. Фактически она характеризует разброс значений x, вычисляемых для многих выборок того же объема. При неограниченном возрастании объема выборки (n→ ) s x→ 0. Иначе говоря, увеличение числа измерений ведет к снижению случайной погрешности x (увеличивает точность). Это снижение пропорционально (n)1/2.

5. Размах варьирования (размах выборки, размах) r = xmax – xmin. Является грубой характеристикой возможных отклонений. Используется при исключении промахов. Схема обработки набора n измерений одной и той же величины: 1) определяют характеристики выборки x, s x 2) проверяют выборку на наличие промахов или выбросов, т. е. элементов, которые значимо отличаются от других. 3) Следующий этап — построение доверительного интервала (confidence region), т. е. интервала дов около x, в котором с заранее заданной доверительной вероятностью Pдов находится точное значение mx. Из определения следует, что | x – mx| дов. Результат представляют в виде mx = x дов. Именно дов чаще всего приводят в качестве оценки погрешности полученной величины x.

2. Отбраковка результатов Чаще всего используют два приема: а) метод "трех сигм" (3 s), если n > 10. Рассчитывают x и s, включая результаты всех измерений. Если |xп – x| > 3 s, то xп исключают из выборки и дальнейшей обработки. б) Q-тест, если n < 10. Выборку располагают в вариационный ряд - по возрастанию полученных значений xi от наименьшего к наибольшему. Подозрительное значение xп может оказаться либо первым, либо последним. Вычисляют величину Q = |xп – xслед|/|xмакс – xмин|, где xслед — значение элемента вариационного ряда, соседнего с подозрительным, |xmax – xmin| — размах варьирования. Сравнивают полученную величину Q с табличной. Если Q > Qтабл, то подозрительное значение исключают. Значения Q-критерия (Qтабл) для уровня значимости 95 %. n 3 4 5 6 7 8 9 10 Qтабл 0, 98 0, 85 0, 73 0, 64 0, 59 0, 54 0, 51 0, 48
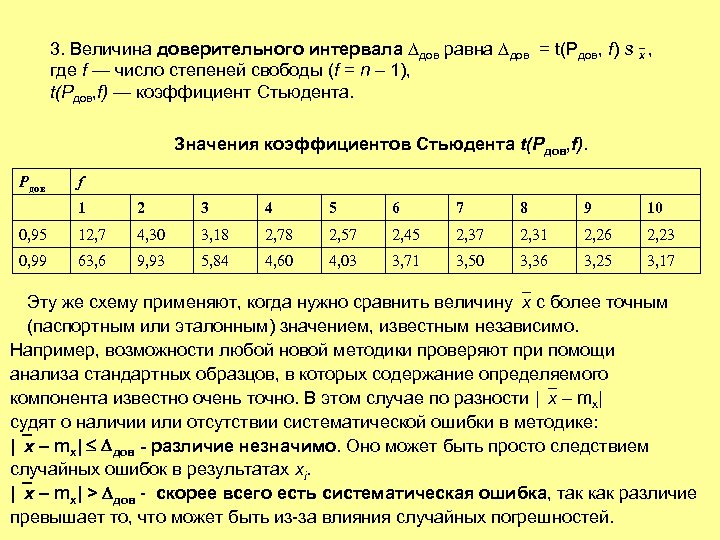
3. Величина доверительного интервала дов равна дов = t(Pдов, f) s x , где f — число степеней свободы (f = n – 1), t(Pдов, f) — коэффициент Стьюдента. Значения коэффициентов Стьюдента t(Pдов, f). Pдов f 1 2 3 4 5 6 7 8 9 10 0, 95 12, 7 4, 30 3, 18 2, 78 2, 57 2, 45 2, 37 2, 31 2, 26 2, 23 0, 99 63, 6 9, 93 5, 84 4, 60 4, 03 3, 71 3, 50 3, 36 3, 25 3, 17 Эту же схему применяют, когда нужно сравнить величину x c более точным (паспортным или эталонным) значением, известным независимо. Например, возможности любой новой методики проверяют при помощи анализа стандартных образцов, в которых содержание определяемого компонента известно очень точно. В этом случае по разности | x – mx| судят о наличии или отсутствии систематической ошибки в методике: | x – mx| дов - различие незначимо. Оно может быть просто следствием случайных ошибок в результатах xi. | x – mx| > дов - скорее всего есть систематическая ошибка, так как различие превышает то, что может быть из-за влияния случайных погрешностей.

Сравнение результатов обработки двух выборок. Например, одна и та же величина измеряется при помощи разных методов или разными людьми. Возникают вопросы: можно ли объединить обе выборки для совместной обработки, или между результатами есть значимое различие. Пусть есть две выборки: {x 1, x 2 … xn} из n точек и {y 1, y 2…ym} из m точек. Статистические критерии позволяют ответить на вопрос: могут ли эти две выборки принадлежать одной генеральной совокупности или это маловероятно. Схема решения: 1) рассчитывают характеристики для обеих выборок x, s x y, s y. 2) При помощи F — критерия сравнивают оценки дисперсий выборок. Для этого рассчитывают величину F = (sx)2/(sy)2, причем в числителе стоит та оценка s 2, которая больше.
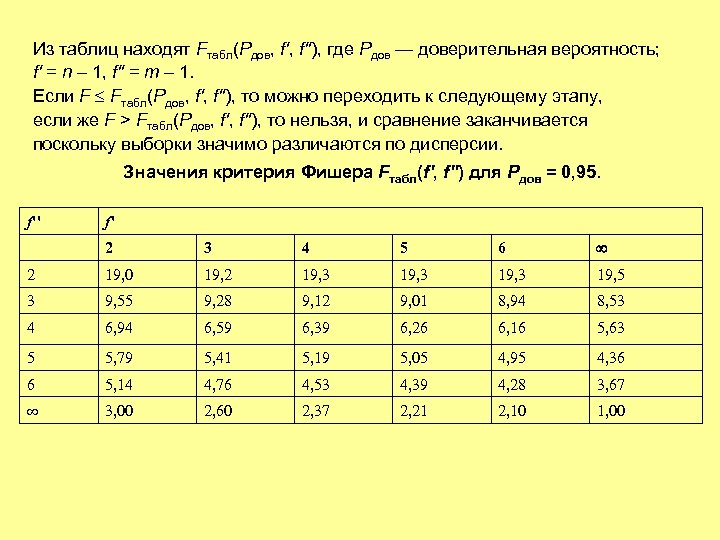
Из таблиц находят Fтабл(Pдов, f''), где Pдов — доверительная вероятность; f' = n – 1, f'' = m – 1. Если F Fтабл(Pдов, f''), то можно переходить к следующему этапу, если же F > Fтабл(Pдов, f''), то нельзя, и сравнение заканчивается поскольку выборки значимо различаются по дисперсии. Значения критерия Фишера Fтабл(f', f'') для Pдов = 0, 95. f'' f' 2 3 4 5 6 2 19, 0 19, 2 19, 3 19, 5 3 9, 55 9, 28 9, 12 9, 01 8, 94 8, 53 4 6, 94 6, 59 6, 39 6, 26 6, 16 5, 63 5 5, 79 5, 41 5, 19 5, 05 4, 95 4, 36 6 5, 14 4, 76 4, 53 4, 39 4, 28 3, 67 3, 00 2, 60 2, 37 2, 21 2, 10 1, 00

3) проверяют различие между x и y при помощи объединенного t-критерия (Стьюдента). Если выполняется неравенство где f = n + m – 2 и t(Pдов, f) — табличная величина критерия Стьюдента для доверительной вероятности Pдов и f степеней свободы, то значимого различия между выборками нет и их можно объединить. После объединения выборок нужно заново рассчитать все характеристики. Если неравенство не выполнено, то значимое различие есть и объединять выборки нельзя.

Распространение (перенос) ошибок при вычислениях. Для случайных ошибок в основе – свойство аддитивности дисперсий независимых случайных величин. Пусть z = a + b + c, тогда z 2 = a 2 + b 2 + c 2. Пусть есть величина z, связанная с величинами x, y, …: z = f(x, y, …). Абсолютные погрешности x, y, … известны и равны соответственно x, y, …. Тогда общее выражение для расчета ошибки z имеет вид ( z)2 = ( f / x)2 ( x)2 + ( f / y)2 ( y)2 + …. Оно справедливо, если погрешности x, y, … являются случайными и независимыми. Соотношения для некоторых простых действий: 1) если z = x + y или z = x – y, то ( z)2 = ( x)2 + ( y)2. 2) если z = x y или z = x / y, то ( z / z)2 = ( x / x)2 + ( y / y)2. 3) если z = lg x = 0. 43 ln x то z = 0, 43 x / x.

Примеры задач 1. Получена серия измерений: 1, 5; 2, 0; 1, 0; 3, 5; 2, 0 (ррm). Оцените матожидание и его доверительный интервал. Решение. Находим x = 2, 1, s = 0, 9, s x = 0, 4. Проверка по Q-тесту показывает отсутствие выбросов: (3, 5 – 2, 5) / (3, 5 – 1, 0) = 0, 4 < 0, 64 (Qтабл для n = 6). Находим доверительный интервал для f = 5: дов = 2. 57 0, 4 = 1. 0. Таким образом, mx = 2, 1 1, 0 = 2 1. Такая высокая случайная погрешность (50 %) нехарактерна для химических методов анализа, для которых она обычно на два порядка ниже. В то же время такая погрешность допустима для многих инструментальных методов анализа, когда речь идет об определении примесей, присутствующих в основном материале в очень низких концентрациях.

2. Получены две серии результатов измерений (%) 3. 40; 3. 50; 3. 60; 3. 51 3. 30; 3. 40; 3. 40 Можно ли их объединить для совместной обработки? Решение. Найдем x, s x и y, s y для обеих выборок: x = 3. 50, sx = 0. 08, s x = 0. 04; y = 3. 35, sy = 0. 06, s y = 0. 02. Рассчитаем Fэксп = ( sx)2/( sy)2 = 1. 8. Это меньше Fтабл = 5. 4, следовательно, можно перейти к сравнению по объединенному критерию Стьюдента. Подставляя найденные величины и определив из табл. , что t(0. 95, 8) = 2. 31, находим, что | x – y| = 0. 05 < 2. 31 0. 044 = 0. 10. Следовательно, выборки можно объединить. После объединения получаем: x = 3. 41, sx = 0. 10, s x = 0. 03. Найдем доверительный интервал: t(0. 95, 9) = 2. 26, дов = 0. 07.

Оценки на максимум (нестатистические) Пригодны не только для случайных, но и для систематических ошибок. Они называются оценками "на максимум" и учитывают самую неблагоприятную ситуацию полного сложения вкладов всех погрешностей. Используют x, y, … — предельные (максимально возможные) погрешности. Выражение для оценок погрешностей имеет вид z = | f / x| x + | f / y| y + …. Отсюда для четырех действий получим: 1) если z = x + y или z = x – y, то z = x + y; 2) если z = x y или z = x / y, то z / z = x / x + y / y.

Некоторые особые моменты Примеры резкого увеличения погрешности рассчитываемой величины при довольно точных исходных данных. 1) малые разности Пусть z = y 1 – y 2, и величина z мала по сравнению с y 1 и y 2. Легко убедиться, что ( z) / z = ( y 1 + y 2) / (y 1 – y 2) и, следовательно, относительная погрешность z может оказаться намного больше относительных погрешностей y 1 и y 2, если знаменатель мал. Например, y 1 = 1, 0 0, 1, y 2 = 0, 9 0, 1 , т. е 10 %. Но тогда z = 0, 1 0, 2, т. е. относительная погрешность z составляет 200 % и полученное значение z вообще не имеет практического смысла. В аналитической химии такая ситуация встречается, когда содержание какого-то компонента определяют по разности, например, при обратном титровании.

2) резкая функция Этот пример относится к случаю, когда для функции z = f(y) производная |df / dy| велика. Поскольку z |(df / dy)| y, то ошибка z тоже может оказаться во много раз больше, чем y. Так, пусть z = y 10 и y = 1, 0 0, 1. Тогда z 10 y 9 y, и приближенная оценка дает z = 1, 0, а более точная z = 1, 5 1, 1. Таким образом, ошибка z очень велика, несмотря на не очень высокую погрешность y. Ситуации с "резкой функцией" характерны на скачках титрования вблизи точек эквивалентности. .

Экспериментальные зависимости. Изучая систему, исследователь обычно может по своему усмотрению задавать значения некоторых переменных хi (факторы (factors)), например, концентраций компонентов, температуры и т. д. После измерений он получает значения свойства уi (i N, где N — общее число измерений) (отклики (response)). Набор данных {уi , хi} - экспериментальная зависимость у(хi). Обычно величины уi и хi определены с ошибкой: xi = xi 0 + хi 0 и yi = yi 0 + уi 0. Часто (но не всегда) ошибками факторов хi пренебрегают. Часто также обоснованно принимают, что случайные погрешности уi и уj независимы. После получения экспериментальной зависимости {уi, хi} следующим является этап принятия или построения модели.

Модель — математическое выражение (формула) или группа выражений, которая без учета погрешностей связывает между собой независимо определяемые величины, в данном случае факторы х с величиной свойства у. Модели: физико-химические и эмпирические. В аналитической химии – градуировочные графики. Mодель имеет вид у = f(х, A), где A — неизвестный параметр или группа (k) параметров. Задачи: 1) оценка параметров А 2) оценка погрешностей параметров 3) оценка погрешности прогноза Примеры моделей: 1) кислотно-основное титрование щелочи кислотой с индикатором. Модель имеет вид Vк = Сщ. Vщ / Ск, оцениваемый параметр Cщ. 2) градуировочный график в спектрофотометрии. Модель имеет вид A = C l, оценивают . 3) потенциометрия — модель: Е = Е 0 + RТ / z. F ln СB, оценивают Е 0.

Пусть есть экспериментальная зависимость {уi, хi} и модель у = f(х, A). Для оценки параметра Am (j = 1—k) нужно построить (найти) выражение вида Am* = Fm(у1, …, у. N, х1, . . . , х. N) = Fm(уi, хi), включающее в себя все значения yi и xi из экспериментальной зависимости. Для нахождения вида Fm(уi, хi) используют два способа — метод наименьших квадратов (МНК) и метод максимума правдоподобия (ММП). Последний метод применяют значительно реже, причем, в случае нормального закона распределения погрешностей результаты оценок совпадают.

В МНК минимизируется сумма S = Pi (yi – f(хi, A))2 → min при постоянных {yi, xi} в пространстве параметров A, что приводит к системе из k уравнений (k — число неизвестных параметров A) вида которую можно разрешить относительно всех Am. В этих уравнениях суммирование ведется по всем экспериментальным точкам, m — номер параметра (m k), Рi = B / i 2 — статистический вес i-го измерения, определяемый с точностью до произвольной константы B, общей для всех точек. В частности, можно положить B = 1. МНК наиболее развит для моделей, линейных относительно оцениваемых параметров, например, у = A 1 f 1(х) + A 2 f 2(х), Оценки погрешностей параметров и прогноза проводят по выражению δ(Am)2 ( Fm / yi)2 δi 2.

Представление результатов вычислений. Значащие цифры Конечный экспериментальный результат (в т. ч. , анализа) принято выражать числом, содержащим только значащие цифры. Значащие цифры — это все достоверно известные цифры плюс первая недостоверная (содержащая погрешность). В качестве погрешности может служить, например, стандартное отклонение или доверительный интервал. Например, если массу образца 0, 06750 г определяли на аналитических весах с точностью до ± 0, 0002 г, то правильное представление результата — 0, 0675 г или 6, 75. 10– 2 г. Нуль, стоящий в середине или в конце числа, является значащей цифрой. Нули, стоящие в начале числа, не являются значащими, они показывают место запятой в десятичной дроби. При отсутствии конкретных данных о погрешностях принимают, что недостоверность последней значащей цифры равна 1. Недостоверность результата вычислений определяется по законам распространения погрешностей. Например, если p. H=4. 27, то [H+] = 5. 4 10– 5 М; Сложение: 53. 7 + 18. 42 = 72. 1

В полумикроанализе (гравиметрия, титриметрия) результат обычно представляют с четырьмя значащими цифрами, что обусловлено точностью измерений массы веществ и объемов растворов. Такой подход принимают в большинстве практических определений. Значащие цифры не являются полноценной заменой статистическому анализу. Они предназначены лишь для представления данных – не завышая точность, и не теряя ее вследствие, например, избыточных округлений. Представление графических данных. Если экспериментальные данные содержат разброс (ошибку), то при графическом представлении не следует соединять все точки между собой, тем более, ломаной линией. Если модель (аналитическое выражение связи) известна, то нужно выполнить обработку данных, найти параметры и привести полученную линию вместе с экспериментальными точками для иллюстрации разброса и качества описания. Если модель неизвестна, то гладкую кривую проводят от руки средним образом.
d46dd365d404b1c28b4499881a3a82a6.ppt