Метод Золотого Сечения.pptx
- Количество слайдов: 15

Министерство Образования и Науки РФ Волгоградский Государственный Технический Университет (Волг. ГТУ) Кафедра «Высшая Математика» Презентация на тему «Метод Золотого Сечения» Работу выполнил: ст. гр. Ап-501 Кашманов Р. Я. Работу проверил: проф. Чигиринская Н. В. Волгоград 2014

Методы Оптимизации (Метод Золотого Сечения) Оптимизация – это выбор наилучшего решения. Математическая теория оптимизации включает в себя фундаментальные результаты и численные методы, позволяющие находить наилучший вариант из множества возможных альтернатив без их полного перебора и сравнения.
![Если известно, что функция f(x) унимодальная на отрезке [a, b], то положение точки минимума Если известно, что функция f(x) унимодальная на отрезке [a, b], то положение точки минимума](https://present5.com/presentation/1/72398118_276379207.pdf-img/72398118_276379207.pdf-3.jpg)
Если известно, что функция f(x) унимодальная на отрезке [a, b], то положение точки минимума можно уточнить, вычислив f(x) в двух внутренних точках отрезка. При этом возможны две ситуации: f(x 1)<f(x 2) Минимум реализуется на отрезке [a, x 2]. f(x 1)>f(x 2) Минимум реализуется на отрезке [x 1, b].

В методе золотого сечения каждая из точек x 1 и x 2 делит исходный интервал на две части так, что отношение целого к большей части равно отношении большей части к меньшей, т. е. равно так называемому "золотому отношению". Это соответствует следующему простому геометрическому представлению: Определение. Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей. Рассмотрим для простоты отрезок [0, 1] единичной длины. Ясно, что на отрезке имеется две таких точки Yo и Zo , они симметричны относительно концов. Точка Yo производит золотое сечение отрезка [A, C] , а точка Zo производит золотое сечение отрезка [BD]. Положим |AB|= x. Тогда |BD|=1 -x. В соответствии с определением точки «золотого сечения» имеем: Решив эту пропорцию, получим :

Стратегия поиска. Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм основан на анализе величин функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
![Алгоритм. Шаг 1. Задать начальный интервал неопределенности Lo=[ao, bo] и требуемую точность ξ >0 Алгоритм. Шаг 1. Задать начальный интервал неопределенности Lo=[ao, bo] и требуемую точность ξ >0](https://present5.com/presentation/1/72398118_276379207.pdf-img/72398118_276379207.pdf-6.jpg)
Алгоритм. Шаг 1. Задать начальный интервал неопределенности Lo=[ao, bo] и требуемую точность ξ >0 Шаг 2. Положить k=0. Шаг 3. Вычислить точки yo=ao+0. 382(ao-bo) и zo=ao+bo-yo Шаг 4. вычислить значения f(yk) , f(zk) Шаг 5. Сравнить значения f(yk) и f(zk) : а) если f(yk) ≤ f(zk) исключить интервал (zk, bk], положить ak+1=a. K bk+1=zk yk+1=ak+1+bk+1 -yk Zk+1=yk Перейти к шагу 6.
![6) если f(yk) > f(zk), то исключить интервал (ak, yk], положить ak+1=yk bk+1=bk yk+1=zk, 6) если f(yk) > f(zk), то исключить интервал (ak, yk], положить ak+1=yk bk+1=bk yk+1=zk,](https://present5.com/presentation/1/72398118_276379207.pdf-img/72398118_276379207.pdf-7.jpg)
6) если f(yk) > f(zk), то исключить интервал (ak, yk], положить ak+1=yk bk+1=bk yk+1=zk, zk+1=ak+1+bk+1 -zk и перейти к шагу 6. Шаг 6. Вычислить Δ=Ιak+1 -bk+1Ι а) если Δ ≤ ξ, то поиск завершен x*є [ak+1, bk+1]. В качестве приближения можно взять середину этого интервала x*=(ak+1+bk+1)/2. б) если Δ > ξ то положить k=k+1 и перейти к шагу 4. Сходимость. Для метода золотого сечения характеристика относительного уменьшения начального интервала неопределенности находится по формуле R(N)=(0, 618)^N-1, где N - количество вычислений функции.

Пример. Используя метод золотого сечения, минимизировать функцию f(х)=x 2+2 х на интервале (-3, 5). Алина конечного интервала не определенности не должна превосходить 0, 2. Решение. Первый шаг. a=-3, b = 5, b-a = 8. x 1= -3 + 0, 362∙ 8 = 0, 056; x 2 = 5 - 0, 382∙ 8 = 1, 944; f(x 1)= 0, 0562 +2∙ 0, 056 =0, 115; f(x 2)= I, 9442 + 2∙ 1, 944=7, 667; f(x 1)<f(x 2). Новый отрезок [-3; 1, 944]. Второй шаг. a=-3, b = 1, 944, b-a =4, 944. x 1 = -3+ 0, 382∙ 4, 944 = -1. 112; x 2= 0, 056; f(x 1)= (-1, 112)2 + 2∙(-1, 112) = -0. 987; f(x 2)=0, 115; f(x 1)<f(x 2). Новый отрезок [-3; 0, 056]. Дальнейшие вычисления оформим в виде таблицы. Значения функции f(x 2), вычисленные на каждом шаге, помечены звездочкой.
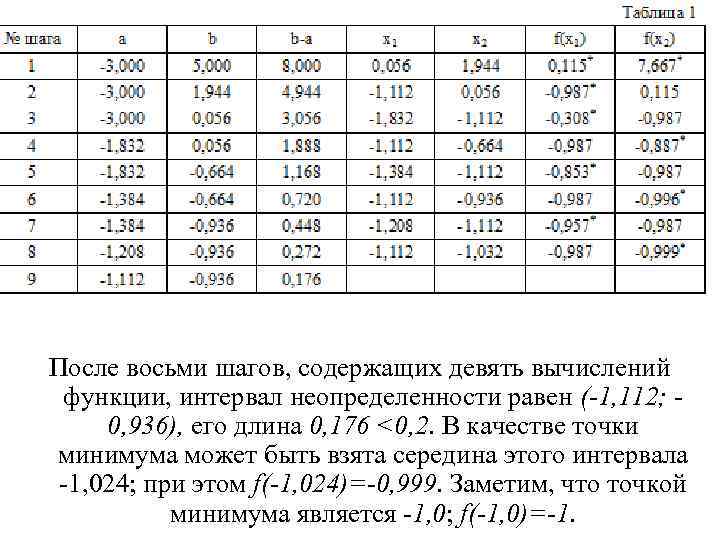
После восьми шагов, содержащих девять вычислений функции, интервал неопределенности равен (-1, 112; 0, 936), его длина 0, 176 <0, 2. В качестве точки минимума может быть взята середина этого интервала 1, 024; при этом f(-1, 024)=-0, 999. Заметим, что точкой минимума является -1, 0; f(-1, 0)=-1.
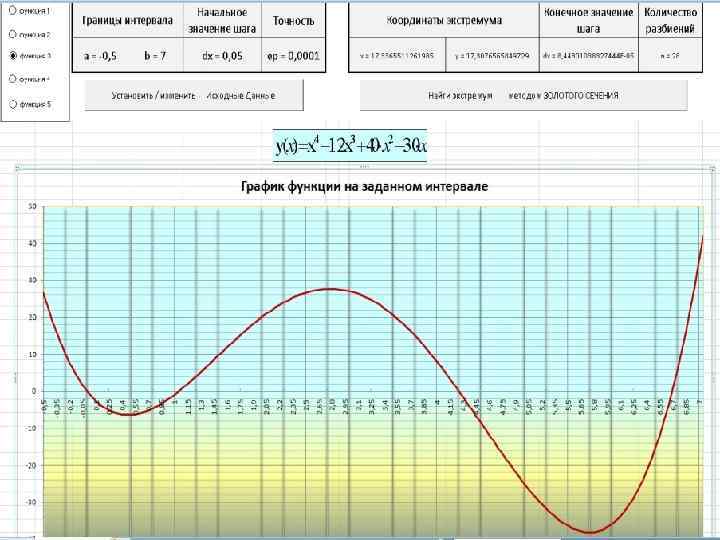
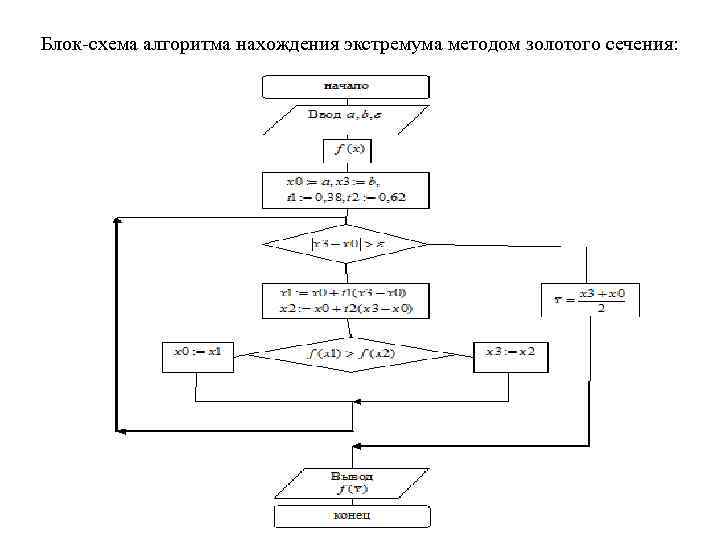
Блок схема алгоритма нахождения экстремума методом золотого сечения:

• 'Нахождение экстремума функции на отрезке. Метод золотого сечения Public Sub the. Algoritm(v 1 As Double, v 2 As Double, v 3 As Double, v 4 As Double, find. Max As Boolean) Dim x 1 As Double, x 2 As Double, y 1 As Double, y 2 As Double, sme As Double Full. Array. Only v 1, v 2, v 3, v 4 'для проверки допустимости аргумента If Not Bad. Dann Then zc = (1 + Sqr(5)) / 2 n = 0 'количество разбиений (переменная модуля класса) Do While b - a > ep sme = (b - a) / zc x 1 = b - sme: x 2 = a + sme y 1 = the. Func(x 1): y 2 = the. Func(x 2) If find. Max Then 'поиск максимума If y 1 <= y 2 Then a = x 1 Else b = x 2 End If Else 'поиск минимума If y 1 >= y 2 Then a = x 1 Else b = x 2 End If n = n + 1 'количество разбиений (переменная модуля класса) Loop dxk = Abs(b - a) ' конечное значение шага xe = (a + b) / 2: ye = the. Func(xe) ' результат: координаты точки экстремума End If End Sub

Microsoft Visual Basic for Applications — это язык программирования, встроенный во множество программ. В частности, во все программы пакета MS Office (и не только). Конечно, MS Office удобен, приятен, незаменим (как мы раньше то без него жили? …) сам по себе, но при использовании VBA, возможности его возрастают неимоверно. Облегчить труд офисных работников VBA поможет даже в том случае, если сами работники его не знают. Лишь бы руководитель у них был умный и пригласив программиста организовал процесс сбора, ввода, проверки и обработки данных используя всю мощь и возможности вычислительной техники. А для студентов и школьников VBA очень удобно изучать. Не нужно никаких дополнительных программ. В любой из офисных программ (Word, Excel, Access и др. ) щелкай Сервис-Макрос-Редактор Visual Basic и экспериментируй. Справочная система отличная, но на английском (хотя в Интернете все можно найти и на русском). Макросы (или макрокоманды) еще один плюс в пользу легкости изучения как языка программирования, так и самого приложения. Включай запись макроса (Сервис-Макрос-Начать Запись. . . ) и производи любые интересующие тебя действия с приложением. А потом рассматривай автоматически записанную процедуру (точный протокол выполняемых тобой действий). Если терпения хватает, то, разобравшись с каждой командой (оператором) по справочной системе, становится ясно, что же и как там внутри происходит. Повторяй те же команды в своей процедуре, корректируй параметры и ты уже программируешь!. . . Было бы желание.

Найдем минимум функции: x 2+ex = 0 Используем для этого Метод золотого сечения. Решение. Положим a 1 = a, b 1 = b. Вычислим λ 1 = a 1 + (1 - 0. 618)(b 1 - a 1), μ 1 = a 1 + 0. 618(b 1 - a 1). Вычислим f(λ 1) = 0. 9209, f(μ 2) = 0. 8284 Итерация № 1. Поскольку f(λ 1) > f(μ 1), то a 2 = -0. 618, b 2 = b 1, λ 2 = -0. 382 μ 2 = a 2 + 0. 618(b 2 - a 2) = -0. 618 + 0. 618(0 - -0. 618), f(μ 2) = f(-0. 2361) = 0. 8284 Итерация № 2. Поскольку f(λ 2) < f(μ 2), то b 3 = -0. 2361, a 3 = a 2, μ 3 = -0. 382 μ 3 = a 3 + 0. 618(b 3 - a 3) = -0. 618 + 0. 618(-0. 2361 - -0. 618), f(μ 3) = f(-0. 382) = 0. 8455 Итерация № 3. Поскольку f(λ 3) > f(μ 3), то a 4 = -0. 4721, b 4 = b 3, λ 4 = -0. 382 μ 4 = a 4 + 0. 618(b 4 - a 4) = -0. 4721 + 0. 618(-0. 2361 - -0. 4721), f(μ 4) = f(-0. 3262) = 0. 8284 Итерация № 4. Поскольку f(λ 4) > f(μ 4), то a 5 = -0. 382, b 5 = b 4, λ 5 = -0. 3262 μ 5 = a 5 + 0. 618(b 5 - a 5) = -0. 382 + 0. 618(-0. 2361 - -0. 382), f(μ 5) = f(-0. 2918) = 0. 8281 Остальные расчеты сведем в таблицу.

N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 an 1 0. 618 0. 4721 0. 382 0. 3607 0. 3557 0. 3538 0. 3526 0. 3521 bn 0 0 0. 2361 0. 2918 0. 3262 0. 3394 0. 3476 0. 3507 0. 3514 bn an 1 0. 618 0. 3819 0. 236 0. 1459 0. 09018 0. 05576 0. 03446 0. 0213 0. 01315 0. 00813 0. 00502 0. 0031 0. 00191 0. 00118 0. 000729 λn 0. 618 0. 382 0. 4721 0. 382 0. 3262 0. 3476 0. 3607 0. 3476 0. 3526 0. 3557 0. 3526 0. 3538 0. 3526 0. 3518 0. 3521 0. 3518 μn 0. 382 0. 2361 0. 382 0. 3262 0. 2918 0. 3262 0. 3476 0. 3394 0. 3476 0. 3526 0. 3507 0. 3526 0. 3518 0. 3514 0. 3518 0. 3517 Находим x как середину интервала [a, b]: x=( 0. 35138422+ 0. 3521134)/2 = 0. 35174881. Параметр сходимости: Ответ: x = 0. 35174881; F(x) = 0. 82718402109927 F(λn) 0. 9209 0. 8284 0. 8466 0. 8284 0. 8281 0. 8272 0. 8273 0. 8272 0. 8272 F(μn) 0. 8284 0. 8455 0. 8284 0. 8281 0. 8321 0. 8281 0. 8272 0. 8274 0. 8272 0. 8272
Метод Золотого Сечения.pptx