Mining Sequence Patterns in Transactional Databases CS 240

Mining Sequence Patterns in Transactional Databases CS 240 B --UCLA Notes by Carlo Zaniolo Based on those by J. Han Data Mining: Concepts and Techniques 1

Sequence Databases & Sequential Patterns z Transaction databases, time-series databases vs. sequence databases z Frequent patterns vs. (frequent) sequential patterns z Applications of sequential pattern mining y. Customer shopping sequences: x. First buy computer, then CD-ROM, and then digital camera, within 3 months. y. Medical treatments, natural disasters (e. g. , earthquakes), science & eng. processes, stocks and markets, etc. y. Telephone calling patterns, Weblog click streams y. DNA sequences and gene structures 2

What Is Sequential Pattern Mining? z Given a set of sequences, find the complete set of frequent subsequences A sequence : < (ef) (ab) (df) c b > A sequence database SID sequence 10 <a(abc)(ac)d(cf)> 20 <(ad)c(bc)(ae)> 30 <(ef)(ab)(df)cb> 40 <eg(af)cbc> An element may contain a set of items. Items within an element are unordered and we list them alphabetically. <a(bc)dc> is a subsequence of <a(abc)(ac)d(cf)> 3

Subsequence • <a(bc)dc> <a(abc)(ac)d(cf)> is a subsequence of Def: S 1 is a subsequence of S 2 if S 1 can be obtained from S 2 by eliminating some of its elements. • This is a partial order, not a lattice. No proper union and intersection operations SID sequence 10 <a(abc)(ac)d(cf)> 20 <(ad)c(bc)(ae)> 30 <(ef)(ab)(df)cb> 40 <eg(af)cbc> A sequence database The pattern <(ab)c> Has support 2 in our Database. 4

The Apriori Property of Sequential Patterns z A basic property: Apriori (Agrawal & Sirkant’ 94) y. If a sequence S is not frequent y. Then none of the super-sequences of S is frequent: antimonotonicity y. E. g, <hb> is infrequent so do <hab> and <(ah)b> Seq. ID Sequence 10 <(bd)cb(ac)> 20 <(bf)(ce)b(fg)> 30 <(ah)(bf)abf> 40 <(be)(ce)d> 50 <a(bd)bcb(ade)> Given support threshold min_sup =2 5

GSP—Generalized Sequential Pattern Mining z GSP (Generalized Sequential Pattern) mining algorithm yproposed by Agrawal and Srikant, EDBT’ 96 z Outline of the method y. Initially, every item in DB is a candidate of length-1 yfor each level (i. e. , sequences of length-k) do xscan database to collect support count for each candidate sequence xgenerate candidate length-(k+1) sequences from length-k frequent sequences using Apriori yrepeat until no frequent sequence or no candidate can be found z Major strength: Candidate pruning by Apriori 6

Finding Length-1 Sequential Patterns z Examine GSP using an example z Initial candidates: all singleton sequences y <a>, , <c>, <d>, <e>, <f>, <g>, <h> z Scan database once, count support for candidates Sup <a> 3 5 <c> 4 <d> min_sup =2 Cand 3 Seq. ID Sequence <e> 3 10 <(bd)cb(ac)> <f> 2 20 <(bf)(ce)b(fg)> <g> 1 30 <(ah)(bf)abf> <h> 1 40 <(be)(ce)d> 50 <a(bd)bcb(ade)> 7

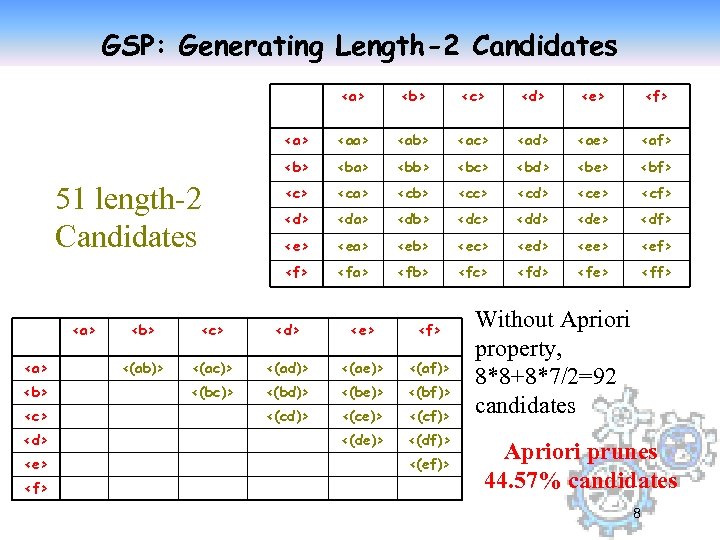
GSP: Generating Length-2 Candidates <a> <c> <d> <e> <f> <aa> <ab> <ac> <ad> <ae> <af> <ba> <bb> <bc> <bd> <be> <bf> <ca> <cb> <cc> <cd> <ce> <cf> <da> <db> <dc> <dd> <de> <df> <ea> <eb> <ec> <ed> <ee> <ef> <a> <d> <a> <c> <a> 51 length-2 Candidates <fa> <fb> <fc> <fd> <fe> <ff> <c> <d> <e> <f> <(ab)> <(ac)> <(ad)> <(ae)> <(af)> <(bc)> <(bd)> <(be)> <(bf)> <(cd)> <(ce)> <(cf)> <(de)> <(df)> <(ef)> Without Apriori property, 8*8+8*7/2=92 candidates Apriori prunes 44. 57% candidates 8

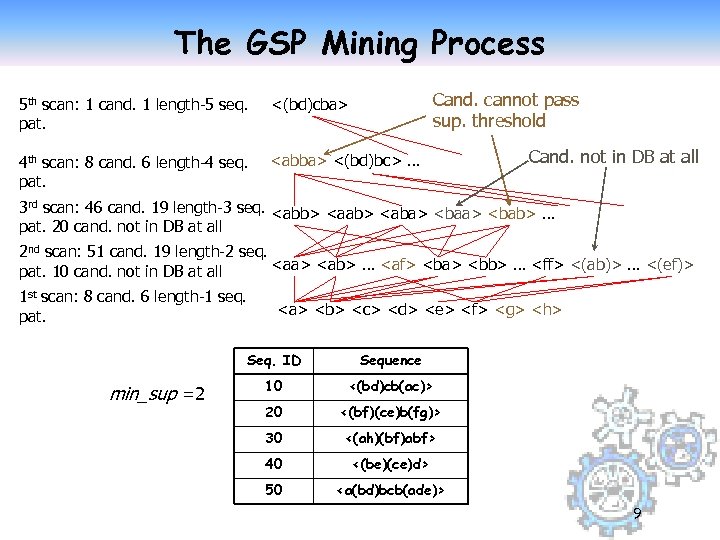
The GSP Mining Process Cand. cannot pass sup. threshold 5 th scan: 1 cand. 1 length-5 seq. pat. <(bd)cba> 4 th scan: 8 cand. 6 length-4 seq. pat. <abba> <(bd)bc> … Cand. not in DB at all 3 rd scan: 46 cand. 19 length-3 seq. <abb> <aab> <aba> <bab> … pat. 20 cand. not in DB at all 2 nd scan: 51 cand. 19 length-2 seq. <aa> <ab> … <af> <ba> <bb> … <ff> <(ab)> … <(ef)> pat. 10 cand. not in DB at all 1 st scan: 8 cand. 6 length-1 seq. pat. <a> <c> <d> <e> <f> <g> <h> Seq. ID min_sup =2 Sequence 10 <(bd)cb(ac)> 20 <(bf)(ce)b(fg)> 30 <(ah)(bf)abf> 40 <(be)(ce)d> 50 <a(bd)bcb(ade)> 9

Candidate Generate-and-test: Drawbacks z A huge set of candidate sequences generated. y Especially 2 -item candidate sequence. z Multiple Scans of database needed. y The length of each candidate grows by one at each database scan. z Inefficient for mining long sequential patterns. y A long pattern grow up from short patterns y The number of short patterns is exponential to the length of mined patterns y Windows can be used to limit the search y Maximum intervals can be imposed between items. z No efficient algorithm at hand for data streams. 10

From Sequential Patterns to Structured Patterns z Sets, sequences, trees, graphs, and other structures y. Transaction DB: Sets of items x{{i 1, i 2, …, im}, …} y. Seq. DB: Sequences of sets: x{<{i 1, i 2}, …, {im, in, ik}>, …} y. Sets of Sequences: x{{, …, <im, in, ik>}, …} y. Sets of trees: {t 1, t 2, …, tn} y. Sets of graphs (mining for frequent subgraphs): x{g 1, g 2, …, gn} z Mining structured patterns in XML documents, biochemical structures, etc. 11

Episodes and Episode Pattern Mining z Other methods for specifying the kinds of patterns y Serial episodes: A B y Parallel episodes: A & B y Regular expressions: (A | B)C*(D E) z Methods for episode pattern mining y Variations of Apriori-like algorithms, e. g. , GSP y Database projection-based pattern growth x. Similar to the frequent pattern growth without candidate generation 12

Periodicity Analysis z Periodicity is everywhere: tides, seasons, daily power consumption, etc. z Full periodicity y Every point in time contributes (precisely or approximately) to the periodicity z Partial periodicit: A more general notion y Only some segments contribute to the periodicity x. Jim reads NY Times 7: 00 -7: 30 am every week day z Cyclic association rules y Associations which form cycles z Methods y Full periodicity: FFT, other statistical analysis methods y Partial and cyclic periodicity: Variations of Apriori-like mining methods 13

Sequential Pattern Mining Algorithms z Concept introduction and an initial Apriori-like algorithm y Agrawal & Srikant. Mining sequential patterns, ICDE’ 95 z Apriori-based method: GSP (Generalized Sequential Patterns: Srikant & Agrawal @ EDBT’ 96) z Pattern-growth methods: Free. Span & Prefix. Span (Han et al. @KDD’ 00; Pei, et al. @ICDE’ 01) z Vertical format-based mining: SPADE (Zaki@Machine Leanining’ 00) z Constraint-based sequential pattern mining (SPIRIT: Garofalakis, Rastogi, Shim@VLDB’ 99; Pei, Han, Wang @ CIKM’ 02) z Mining closed sequential patterns: Clo. Span (Yan, Han & Afshar @SDM’ 03) 14

Ref: Mining Sequential Patterns z R. Srikant and R. Agrawal. Mining sequential patterns: Generalizations and performance improvements. EDBT’ 96. z H. Mannila, H Toivonen, and A. I. Verkamo. Discovery of frequent episodes in event sequences. DAMI: 97. z M. Zaki. SPADE: An Efficient Algorithm for Mining Frequent Sequences. Machine Learning, 2001. z J. Pei, J. Han, H. Pinto, Q. Chen, U. Dayal, and M. -C. Hsu. Prefix. Span: Mining Sequential Patterns Efficiently by Prefix-Projected Pattern Growth. ICDE'01 (TKDE’ 04). z J. Pei, J. Han and W. Wang, Constraint-Based Sequential Pattern Mining in Large Databases, CIKM'02. z X. Yan, J. Han, and R. Afshar. Clo. Span: Mining Closed Sequential Patterns in Large Datasets. SDM'03. z J. Wang and J. Han, BIDE: Efficient Mining of Frequent Closed Sequences, ICDE'04. z H. Cheng, X. Yan, and J. Han, Inc. Span: Incremental Mining of Sequential Patterns in Large Database, KDD'04. z J. Han, G. Dong and Y. Yin, Efficient Mining of Partial Periodic Patterns in Time Series Database, ICDE'99. z J. Yang, W. Wang, and P. S. Yu, Mining asynchronous periodic patterns in time series data, KDD'00. 15