Mining Multiple-level Association Rules in Large Databases IEEE

Mining Multiple-level Association Rules in Large Databases IEEE Transactions on Knowledge and Data Engineering, 1999 Authors : JIAWEI HAN, Simon Fraser University, British Columbia. YONGJIAN FU, University of Missouri-Rolla, Missouri. Presenter : Zhenyu Lu (based on Mohammed’s previous slides, with some changes)

Outline n Introduction n Algorithm n Performance studies n Cross-level association n Filtering of uninteresting association rules n Conclusions

Introduction: Why Multiple-Level Association Rules? TID items T 1 {m 1, b 2} T 2 {m 2, b 1} T 3 Frequent itemset: {b 2} A. A rules: none Is this database useless?

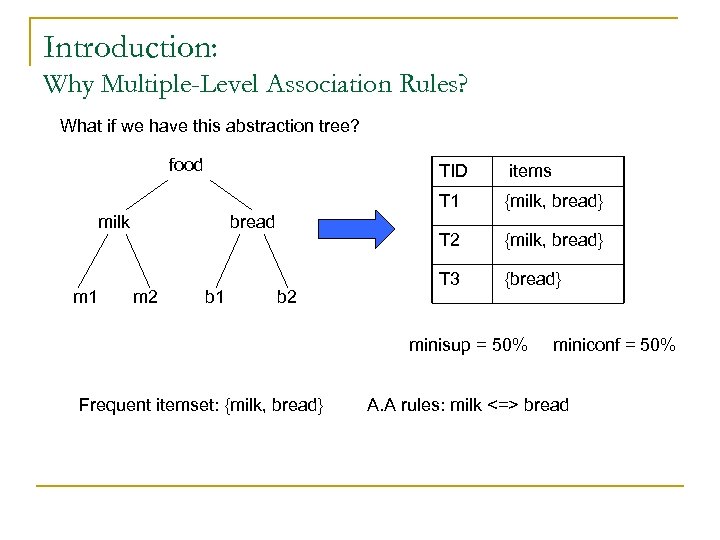
Introduction: Why Multiple-Level Association Rules? What if we have this abstraction tree? food TID T 1 milk m 1 m 2 b 1 b 2 {milk, bread} T 2 bread items {milk, bread} T 3 {bread} minisup = 50% Frequent itemset: {milk, bread} miniconf = 50% A. A rules: milk <=> bread

Introduction: Why Multiple-Level Association Rules? • Sometimes, at primitive data level, data does not show any significant pattern. But there are useful information hiding behind. • The goal of Multiple-Level Association Analysis is to find the hidden information in or between levels of abstraction

Introduction: Requirements in Multiple-Level Association Analysis Two general requirements to do multiple-level association rule mining: 1) Provide data at multiple levels of abstraction. (a common practice now) 2) Find efficient methods for multiple-level rule mining. (our focus)

Outline n Introduction n Algorithm n Performance studies n Cross-level association n Filtering of uninteresting association rules n Conclusions

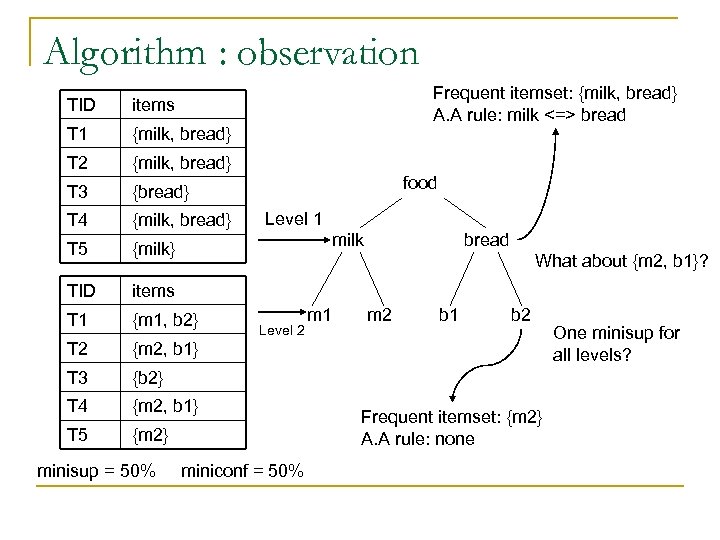
Algorithm : observation TID T 1 {milk, bread} T 2 {milk, bread} T 3 {bread} T 4 {milk, bread} T 5 {milk} TID items T 1 {m 1, b 2} T 2 {m 2, b 1} T 3 {b 2} T 4 {m 2, b 1} T 5 Frequent itemset: {milk, bread} A. A rule: milk <=> bread items {m 2} minisup = 50% food Level 1 milk bread What about {m 2, b 1}? Level 2 miniconf = 50% m 1 m 2 b 1 b 2 Frequent itemset: {m 2} A. A rule: none One minisup for all levels?

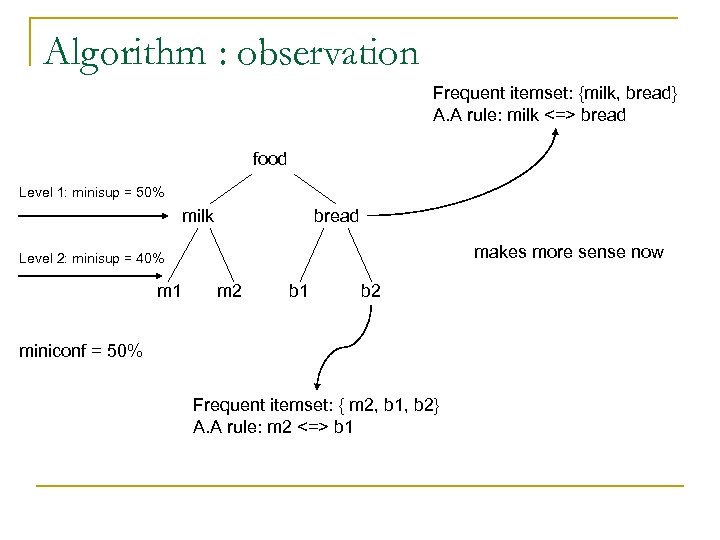
Algorithm : observation Frequent itemset: {milk, bread} A. A rule: milk <=> bread food Level 1: minisup = 50% milk bread makes more sense now Level 2: minisup = 40% m 1 m 2 b 1 b 2 miniconf = 50% Frequent itemset: { m 2, b 1, b 2} A. A rule: m 2 <=> b 1

Algorithm : observation Drawbacks to use only one minisup: • If the minisup is too high, we are losing information from lower levels • If the minisup is too low, we are gaining too many rules from higher levels, many of them are useless food Approach: ascending minisup on each level milk m 1 minisup bread m 2 b 1 b 2

$Algorithm: An Example An entry of sales_transaction Table Transaction_id Bar_code_set 351428 {17325, 92108, 55349,$

Algorithm: An Example An entry of sales_transaction Table Transaction_id Bar_code_set 351428 {17325, 92108, 55349, 88157, …} A sales_item Description Relation Bar_code category Brand Content Size Storage_pd price 17325 Milk Foremost 2% 1 ga. 14(days) $3. 89

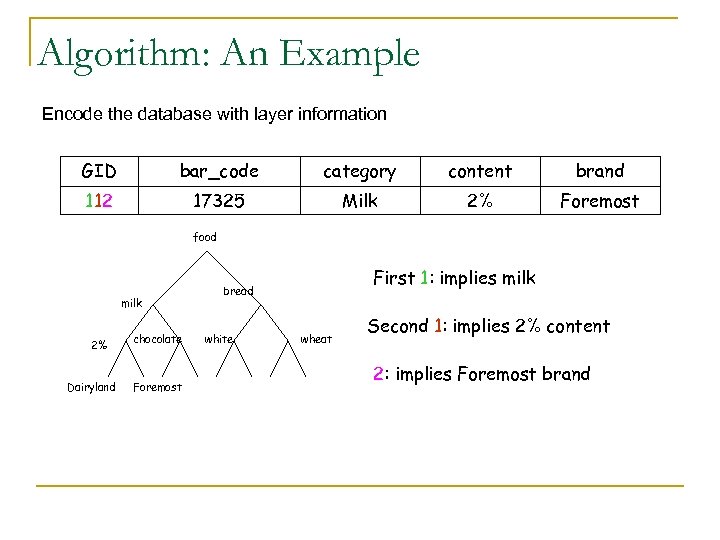
Algorithm: An Example Encode the database with layer information GID bar_code category content brand 112 17325 Milk 2% Foremost food milk 2% Dairyland chocolate Foremost First 1: implies milk bread white wheat Second 1: implies 2% content 2: implies Foremost brand

Algorithm: An Example Encoded Transaction Table: T[1] TID Items T 1 {111, 121, 211, 221} T 2 {111, 222, 323} T 3 {112, 122, 221, 411} T 4 {111, 121} T 5 {111, 122, 211, 221, 413} T 6 {211, 323, 524} T 7 {323, 411, 524, 713}

Algorithm: An Example The frequent 1 -itemset on level 1 L[1, 1] Itemset Support {1**} 5 {2**} Level-1 minsup = 4 only keep items in L[1, 1] from T[1] 5 T[2] TID Items Support {1**, 2**} 4 Use Apriori on each level {111, 222} T 3 Itemset {111, 121, 211, 221} T 2 L[1, 2] T 1 {112, 122, 221} T 4 {111, 121} T 5 {111, 122, 211, 221} T 6 {211}

Algorithm: An Example Level-2 minsup = 3 L[2, 2] {11*} 5 {12*} 4 {21*} 4 {22*} 4 4 {11*, 21*} Itemset Support {11*, 12*} L[2, 1] Itemset 3 {11*, 22*} 4 {12*, 22*} 3 {21*, 22*} 3 L[2, 3] Itemset Support {11*, 12*, 22*} 3 {11*, 22*} 3

Frequent Item Sets at Level 3 L[3, 1] Level-3 minsup = 3 Itemse t Support {111} 4 {221} 3 L[3, 2] Itemset Support {111, 211} 3 Only generate T[1] & T[2], all frequent itemsets after level 2 is generated from T[2] E. g. Level-1: 80% of customers that purchase milk also purchase bread. milk bread with Confidence= 80% Level-2: 75% of people who buy 2% milk also buy wheat bread. 2% milk wheat bread with Confidence= 75%

Algorithm ML_T 2 L 1 q q q Purpose: To find multiple-level frequent item sets for mining strong association rules in a transaction database Input n T[1]: a hierarchy-information encoded transaction table of form <TID, Item-set> n minisup threshold for each level L in the form: (minsup[L]) Output: Multiple-level frequent item sets

Algorithm variations n n n Algorithm ML_T 1 LA q Use only the first encoded transaction table T[1]. q Support for the candidate sets at all levels computed at the same time. q pros: Only one table and maximum k-scans q cons: May consist of infrequent items and requires large space. Algorithm ML_TML 1 q Generate multiple encoded transaction tables T[1], …, T[max_l+1] q Pros: May save substantial amount of processing q Cons: Can be inefficient if only a few items are filtered out at each level processed. Algorithm ML_T 2 LA q Uses 2 encoded transaction tables as in ML_T 2 L 1 algorithm. q Support for the candidate sets at all levels computed at the same time. q Pros: Potentially efficient if T[2] consists of much fewer items than T[1]. q Cons: ?

Outline n Introduction n Algorithm n Performance studies n Cross-level association n Filtering of uninteresting association rules n Conclusions

Performance Study n Assumptions: q q n The maximal level in concept hierarchy is 3 Use two data sets DB 1 (Average frequent item length = 4 and Average transaction size =10) and DB 2 (Average frequent item length = 6 and Average transaction size =20) Conclusions: q q q Relative performance of the four algorithms is highly relevant to the threshold setting (i. e. , the power of a filter at each level). Parallel derivation of L(l, k) is useful and deriving a transaction table T(2) is usually beneficial. ML_T 1 LA is found to be the BEST or the second best algorithm.

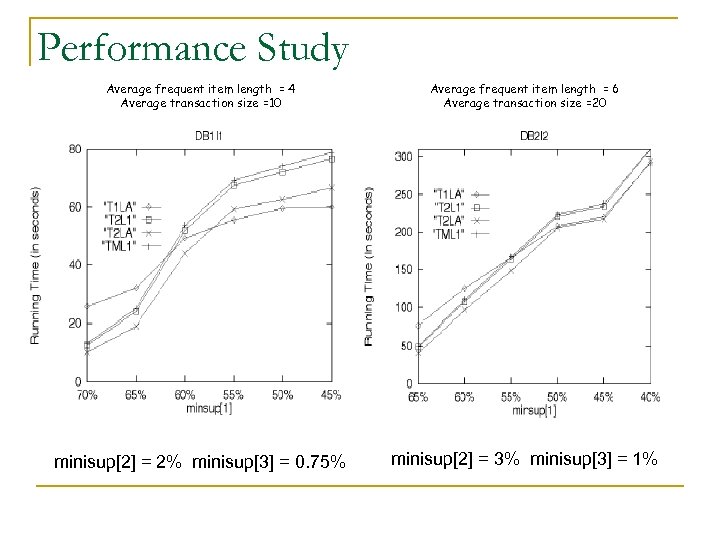
Performance Study Average frequent item length = 4 Average transaction size =10 Average frequent item length = 6 Average transaction size =20 minisup[2] = 2% minisup[3] = 0. 75% minisup[2] = 3% minisup[3] = 1%

Performance Study Average frequent item length = 4 Average transaction size =10 minisup[1] = 60% minisup[3] = 0. 75% Average frequent item length = 6 Average transaction size =20 minisup[1] = 55% minisup[3] = 1%

Performance Study minisup[1] = 60% minisup[2] = 2% minisup[1] = 55% minisup[2] = 3%

Performance Study Two interesting performance features: • The performance of algorithm is highly relative to minisup, especially minisup[1] & minisup[2]. • T[2] is beneficial

Outline n Introduction n Algorithm n Performance studies n Cross-level association n Filtering of uninteresting association rules n Conclusions

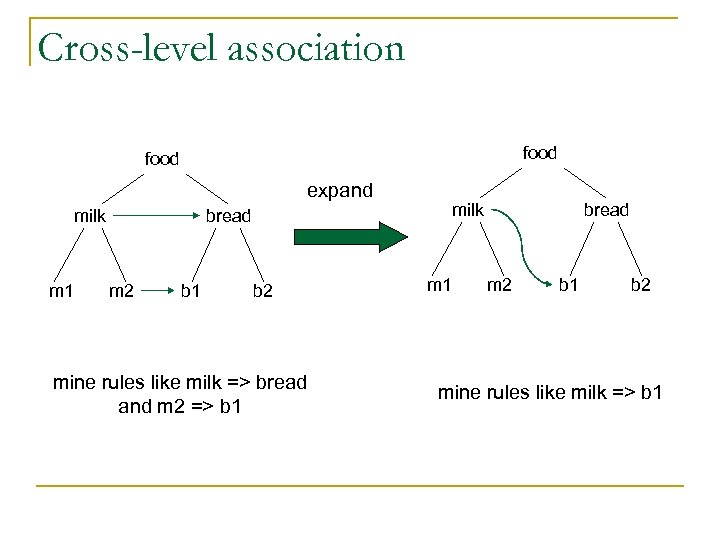
Cross-level association food expand milk m 1 milk bread m 2 b 1 b 2 mine rules like milk => bread and m 2 => b 1 m 1 bread m 2 b 1 b 2 mine rules like milk => b 1

Cross-level association Two adjustments: • A single minisup is used at all levels • When the frequent k-itemsets are generated, items at all levels are considered, itemsets which contain an item and its ancestor are excluded

Outline n Introduction n Algorithm n Performance studies n Cross-level association n Filtering of uninteresting association rules n Conclusions

Filtering of uninteresting association rules n Removal of redundant rules: • To remove redundant rules, when a rule R passes the minimum confidence test, it is checked against every strong rule R' , of which R is a descendant. If the confidence of R, (R), falls in the range of the expected confidence with the variation of , it is removed. • • Example: • milk bread(12% sup, 85% con) • Chocolate milk bread(1% sup, 84% con) • Not interesting if 8% of milk is chocolate milk Can reduce rules by 30% to 60%

Filtering of uninteresting association rules (continued) n Removal of unnecessary rules: • • To filter out unnecessary association rules, for each strong rule R’ : A => B, we test every such rule R : A ‑ C => B, where C belongs to A. If the confidence of R, (R), is not significantly different from that of R' , (R' ), R is removed. Example: • • • 80% customer buy milk => bread 80% customer buy milk + butter => bread Reduces rules by 50% to 80%

Conclusions n n n Extended the association rules from single-level to multiplelevel. A top-down progressive deepening technique is developed for mining multiple-level association rules. Filtering of uninteresting association rules.

Exams Questions n Q 1: Give an example of multilevel association rules? n A: Besides finding the 80% of customers that purchase milk may also purchase bread, it is interesting to allow users to drill-down and show that 75% of people buy wheat bread if they buy 2 percent milk.

Exams Questions n n Q 2: What are the problems in using normal Apiori methods? ? A: One may apply the Apriori algorithm to examine data items at multiple levels of abstraction under the same minimum support and minimum confidence thresholds. This direction is simple, but it may lead to some undesirable results. First, large support is more likely to exist at high levels of abstraction. If one wants to find strong associations at relatively low levels of abstraction, the minimum support threshold must be reduced substantially; this may lead to the generation of many uninteresting associations at high or intermediate levels. Second, since it is unlikely to find many strong association rules at a primitive concept level, mining strong associations should be performed at a rather high concept level, which is actually the case in many studies. However, mining association rules at high concept levels may often lead to the rules corresponding to prior knowledge and expectations, such as “milk => bread”, (which could be common sense), or lead to some uninteresting attribute combinations if the minimum support is allowed to be rather small, such as “toy => milk”, (which may just happen together by chance).

Exams Questions n n Q 3: What are the 2 general steps to do multiple-level association rule mining? A: To explore multiple-level association rule mining, one needs to provide: 1) Data at multiple levels of abstraction, and 2) Efficient methods for multiple-level rule mining.