af8650e4e4dcb8768eeb6cf1ff749fd1.ppt
- Количество слайдов: 152

Mining Big Data in Health Care Vipin Kumar Department of Computer Science University of Minnesota kumar@cs. umn. edu www. cs. umn. edu/~kumar

Introduction
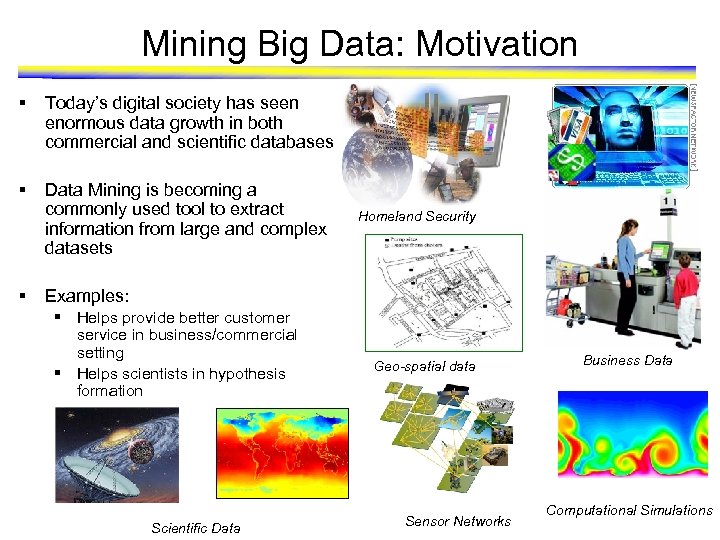
Mining Big Data: Motivation § Today’s digital society has seen enormous data growth in both commercial and scientific databases § Data Mining is becoming a commonly used tool to extract information from large and complex datasets § Homeland Security Examples: § Helps provide better customer service in business/commercial setting § Helps scientists in hypothesis formation Scientific Data Geo-spatial data Sensor Networks Business Data Computational Simulations
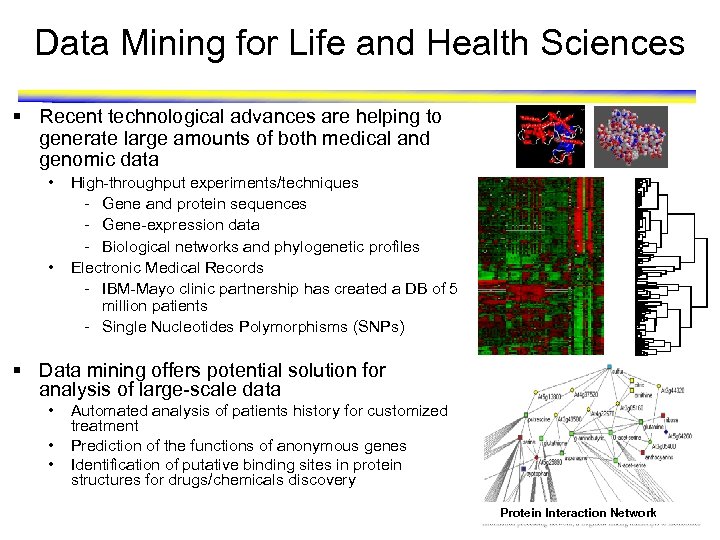
Data Mining for Life and Health Sciences § Recent technological advances are helping to generate large amounts of both medical and genomic data • • High-throughput experiments/techniques - Gene and protein sequences - Gene-expression data - Biological networks and phylogenetic profiles Electronic Medical Records - IBM-Mayo clinic partnership has created a DB of 5 million patients - Single Nucleotides Polymorphisms (SNPs) § Data mining offers potential solution for analysis of large-scale data • • • Automated analysis of patients history for customized treatment Prediction of the functions of anonymous genes Identification of putative binding sites in protein structures for drugs/chemicals discovery Protein Interaction Network
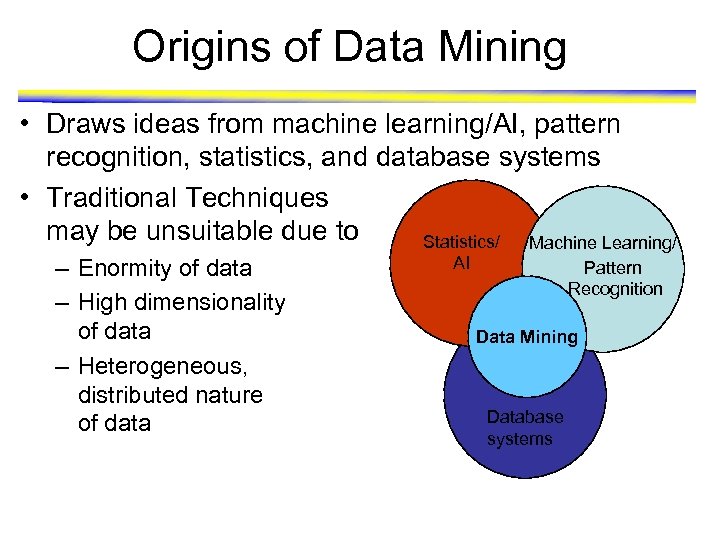
Origins of Data Mining • Draws ideas from machine learning/AI, pattern recognition, statistics, and database systems • Traditional Techniques may be unsuitable due to Statistics/ Machine Learning/ – Enormity of data – High dimensionality of data – Heterogeneous, distributed nature of data AI Pattern Recognition Data Mining Database systems
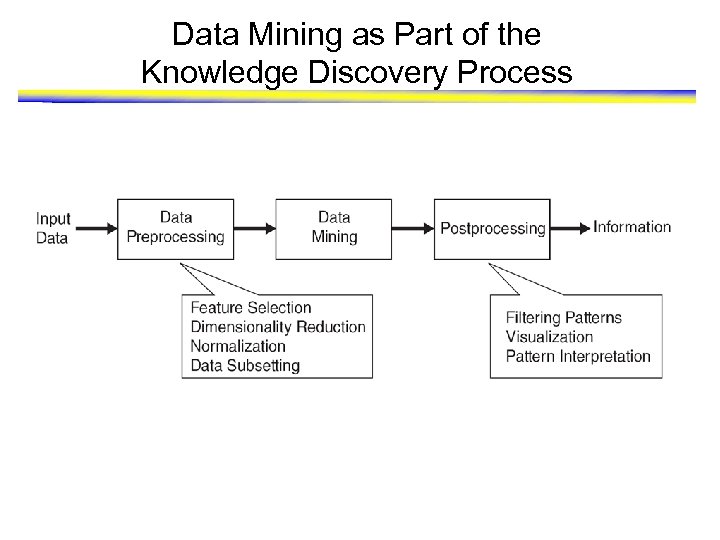
Data Mining as Part of the Knowledge Discovery Process
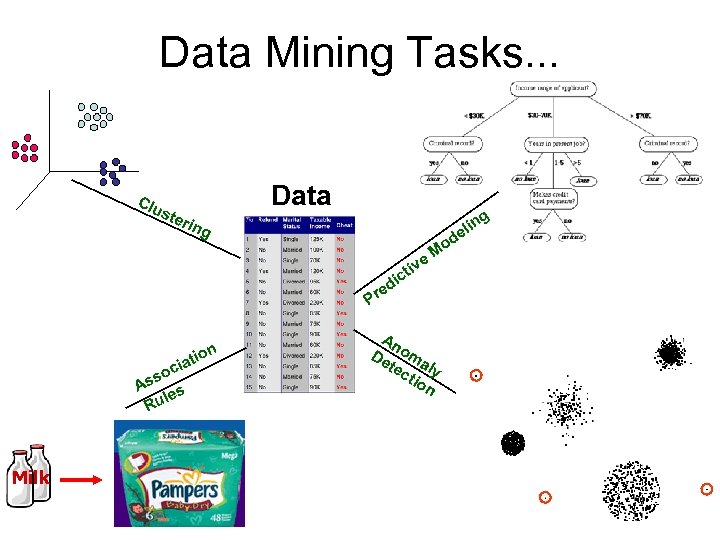
Data Mining Tasks. . . Clu Data ste g rin n eli d g ion t cia so As s le Ru Milk iv ict d e Pr Mo e An De oma tec ly tio n

Predictive Modeling: Classification
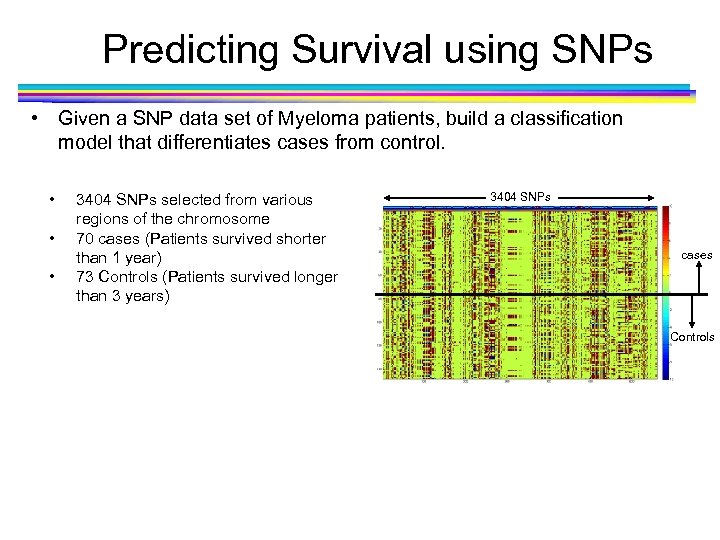
Predicting Survival using SNPs • Given a SNP data set of Myeloma patients, build a classification model that differentiates cases from control. • • • 3404 SNPs selected from various regions of the chromosome 70 cases (Patients survived shorter than 1 year) 73 Controls (Patients survived longer than 3 years) 3404 SNPs cases Controls

Examples of Classification Task • Predicting tumor cells as benign or malignant • Classifying secondary structures of protein as alpha-helix, beta-sheet, or random coil • Predicting functions of proteins • Classifying credit card transactions as legitimate or fraudulent • Categorizing news stories as finance, weather, entertainment, sports, etc • Identifying intruders in the cyberspace
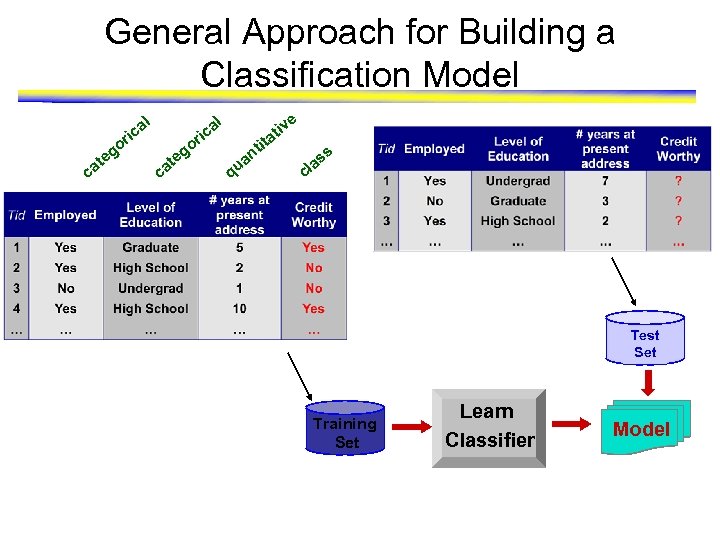
General Approach for Building a Classification Model l o ca g te e tiv a tit n l a ic r o ca g te a ic r q ua s as l c Test Set Training Set Learn Classifier Model

Commonly Used Classification Models • Base Classifiers – – – Decision Tree based Methods Rule-based Methods Nearest-neighbor Neural Networks Naïve Bayes and Bayesian Belief Networks Support Vector Machines • Ensemble Classifiers – Boosting, Bagging, Random Forests
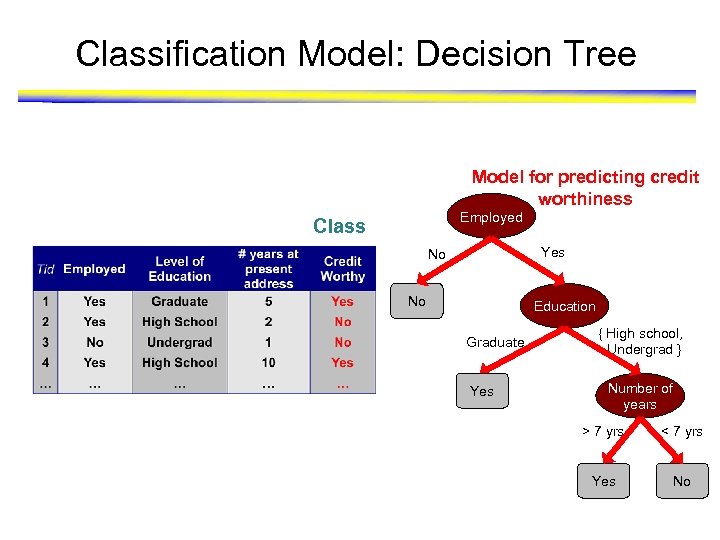
Classification Model: Decision Tree Model for predicting credit worthiness Employed Class Yes No No Education Graduate Yes { High school, Undergrad } Number of years > 7 yrs < 7 yrs Yes No
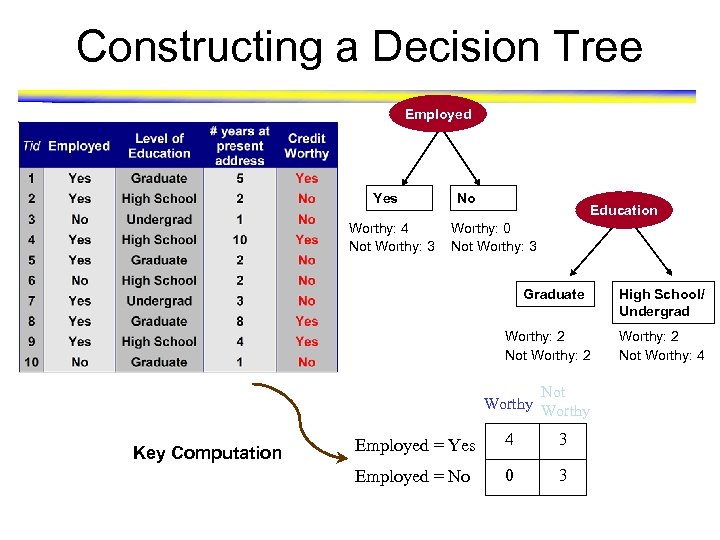
Constructing a Decision Tree Employed Yes Worthy: 4 Not Worthy: 3 No Education Worthy: 0 Not Worthy: 3 Graduate Worthy: 2 Not Worthy Key Computation Employed = Yes 4 3 Employed = No 0 3 High School/ Undergrad Worthy: 2 Not Worthy: 4
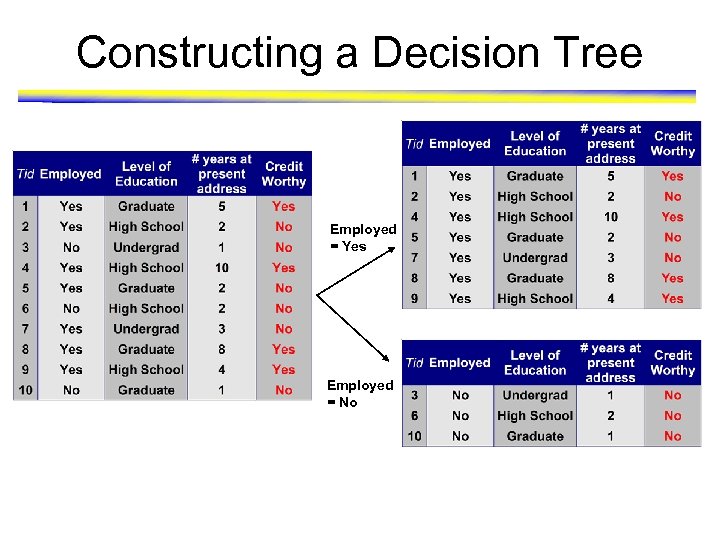
Constructing a Decision Tree Employed = Yes Employed = No

Design Issues of Decision Tree Induction • How should training records be split? – Method for specifying test condition • depending on attribute types – Measure for evaluating the goodness of a test condition • How should the splitting procedure stop? – Stop splitting if all the records belong to the same class or have identical attribute values – Early termination

How to determine the Best Split l Greedy approach: – Nodes with purer class distribution are preferred l Need a measure of node impurity: High degree of impurity Low degree of impurity

Measure of Impurity: GINI • Gini Index for a given node t : (NOTE: p( j | t) is the relative frequency of class j at node t). – Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information – Minimum (0. 0) when all records belong to one class, implying most interesting information

Measure of Impurity: GINI • Gini Index for a given node t : (NOTE: p( j | t) is the relative frequency of class j at node t). – For 2 -class problem (p, 1 – p): • GINI = 1 – p 2 – (1 – p)2 = 2 p (1 -p)

Computing Gini Index of a Single Node P(C 1) = 0/6 = 0 P(C 2) = 6/6 = 1 Gini = 1 – P(C 1)2 – P(C 2)2 = 1 – 0 – 1 = 0 P(C 1) = 1/6 P(C 2) = 5/6 Gini = 1 – (1/6)2 – (5/6)2 = 0. 278 P(C 1) = 2/6 P(C 2) = 4/6 Gini = 1 – (2/6)2 – (4/6)2 = 0. 444

Computing Gini Index for a Collection of Nodes l When a node p is split into k partitions (children) where, ni = number of records at child i, n = number of records at parent node p. l Choose the attribute that minimizes weighted average Gini index of the children l Gini index is used in decision tree algorithms such as CART, SLIQ, SPRINT

Binary Attributes: Computing GINI Index l l Splits into two partitions Effect of Weighing partitions: – Larger and Purer Partitions are sought for. B? Yes Gini(N 1) = 1 – (5/6)2 – (1/6)2 = 0. 278 Gini(N 2) = 1 – (2/6)2 – (4/6)2 = 0. 444 Node N 1 No Node N 2 Weighted Gini of N 1 N 2 = 6/12 * 0. 278 + 6/12 * 0. 444 = 0. 361 Gain = 0. 486 – 0. 361 = 0. 125

Continuous Attributes: Computing Gini Index l Use Binary Decisions based on one value l Several Choices for the splitting value – Number of possible splitting values = Number of distinct values l Each splitting value has a count matrix associated with it – Class counts in each of the partitions, A < v and A v l Simple method to choose best v – For each v, scan the database to gather count matrix and compute its Gini index – Computationally Inefficient! Repetition of work. ≤ 80 > 80 Yes 0 3 No 3 4

Decision Tree Based Classification l Advantages: – – Inexpensive to construct Extremely fast at classifying unknown records Easy to interpret for small-sized trees Robust to noise (especially when methods to avoid overfitting are employed) – Can easily handle redundant or irrelevant attributes (unless the attributes are interacting) l Disadvantages: – Space of possible decision trees is exponentially large. Greedy approaches are often unable to find the best tree. – Does not take into account interactions between attributes – Each decision boundary involves only a single attribute
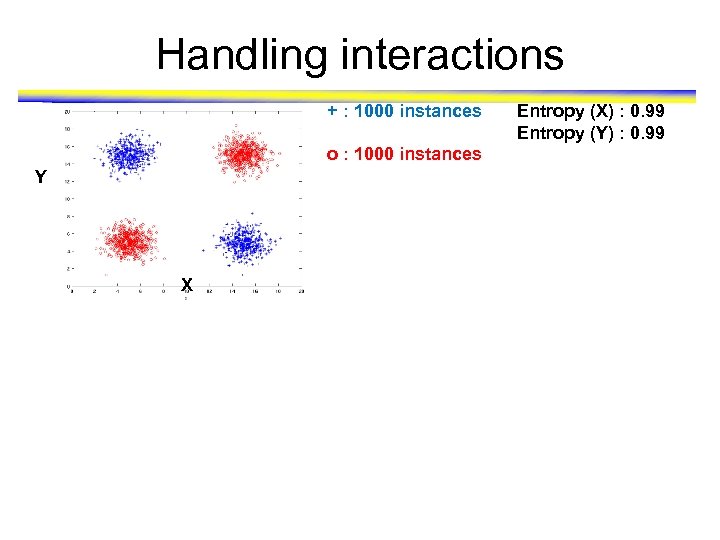
Handling interactions + : 1000 instances o : 1000 instances Y X Entropy (X) : 0. 99 Entropy (Y) : 0. 99
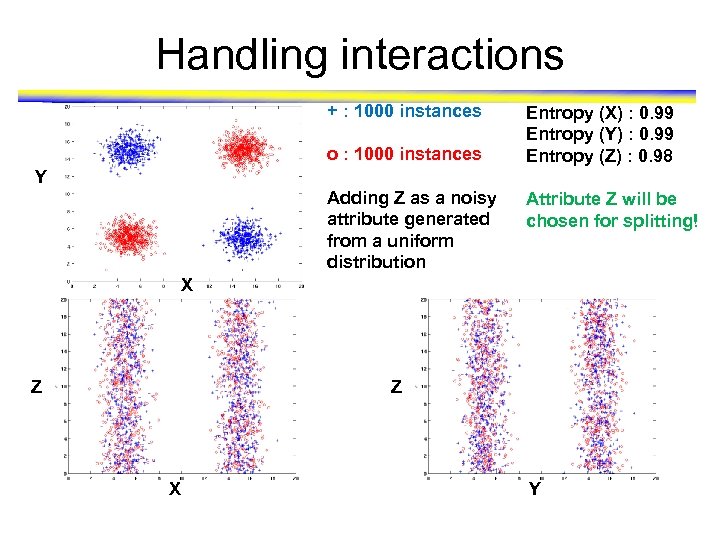
Handling interactions + : 1000 instances o : 1000 instances Entropy (X) : 0. 99 Entropy (Y) : 0. 99 Entropy (Z) : 0. 98 Y Adding Z as a noisy attribute generated from a uniform distribution Attribute Z will be chosen for splitting! X Z Z X Y
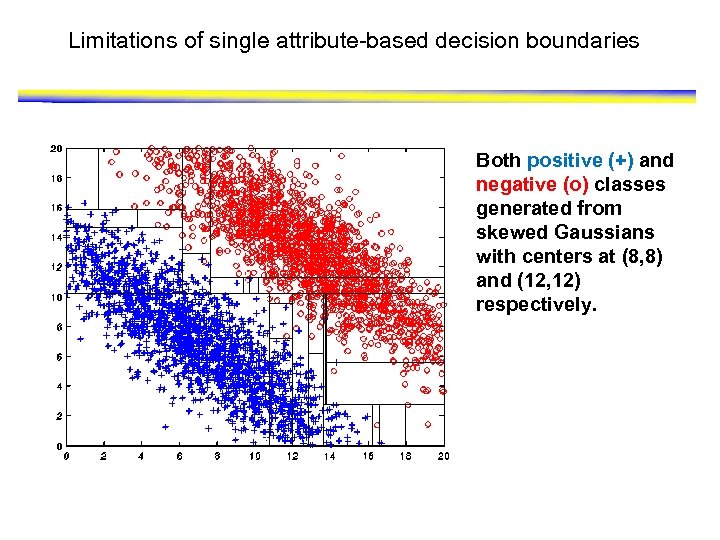
Limitations of single attribute-based decision boundaries Both positive (+) and negative (o) classes generated from skewed Gaussians with centers at (8, 8) and (12, 12) respectively.

Model Overfitting

Classification Errors • Training errors (apparent errors) – Errors committed on the training set • Test errors – Errors committed on the test set • Generalization errors – Expected error of a model over random selection of records from same distribution
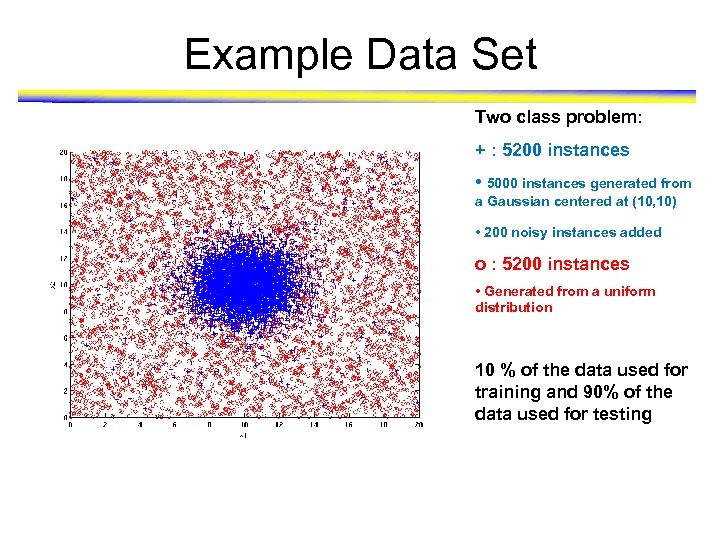
Example Data Set Two class problem: + : 5200 instances • 5000 instances generated from a Gaussian centered at (10, 10) • 200 noisy instances added o : 5200 instances • Generated from a uniform distribution 10 % of the data used for training and 90% of the data used for testing
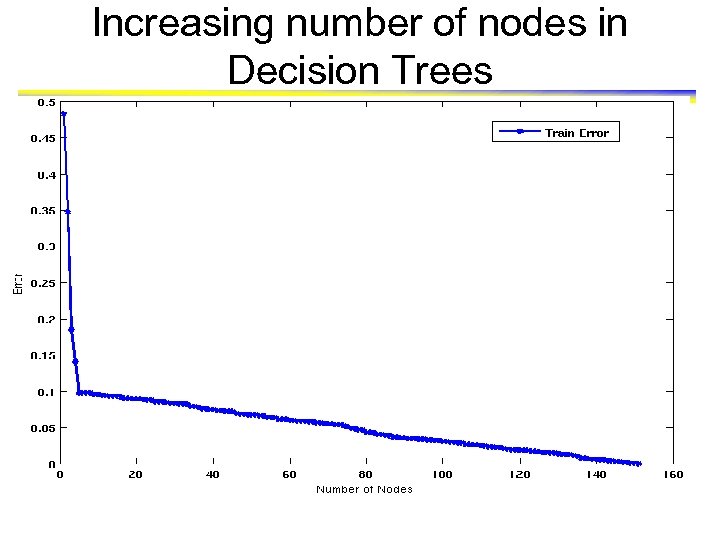
Increasing number of nodes in Decision Trees
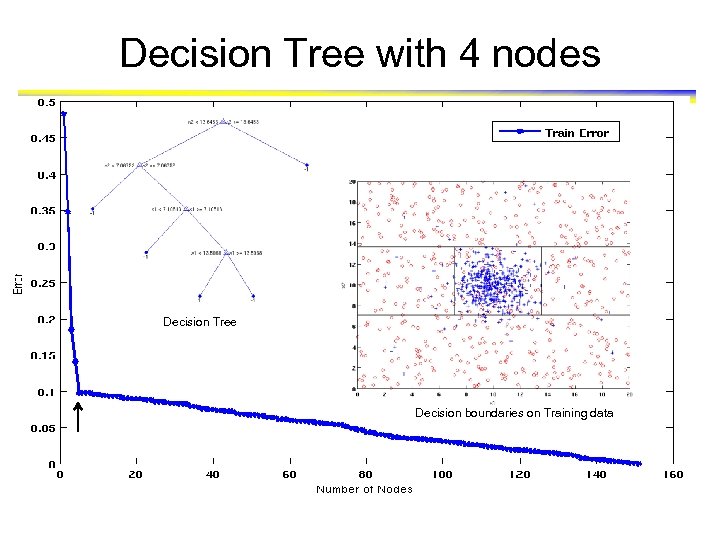
Decision Tree with 4 nodes Decision Tree Decision boundaries on Training data
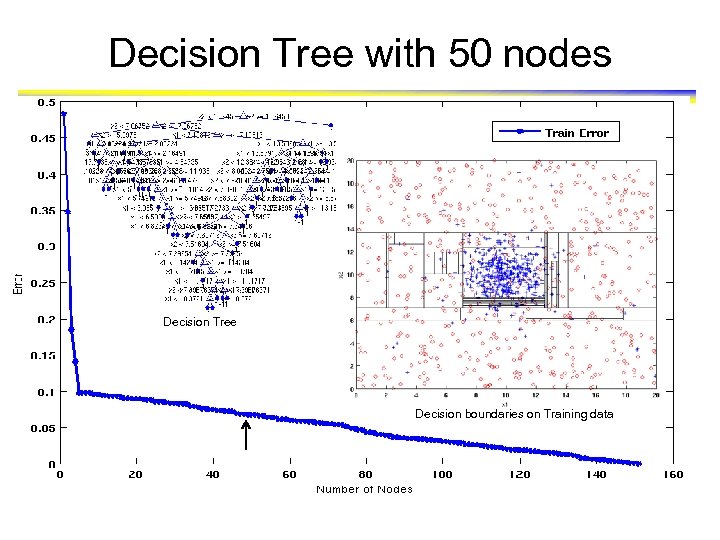
Decision Tree with 50 nodes Decision Tree Decision boundaries on Training data
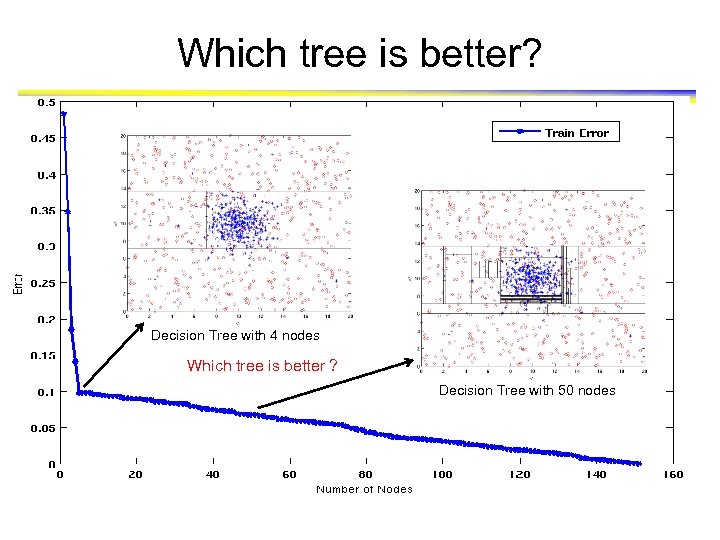
Which tree is better? Decision Tree with 4 nodes Which tree is better ? Decision Tree with 50 nodes
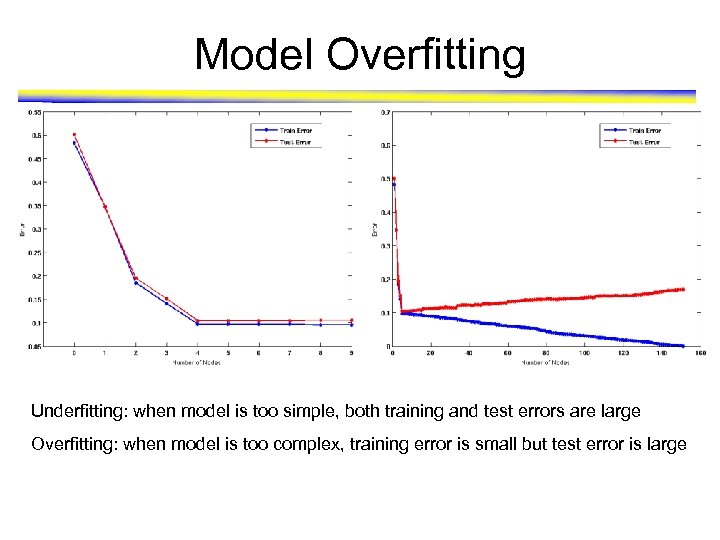
Model Overfitting Underfitting: when model is too simple, both training and test errors are large Overfitting: when model is too complex, training error is small but test error is large
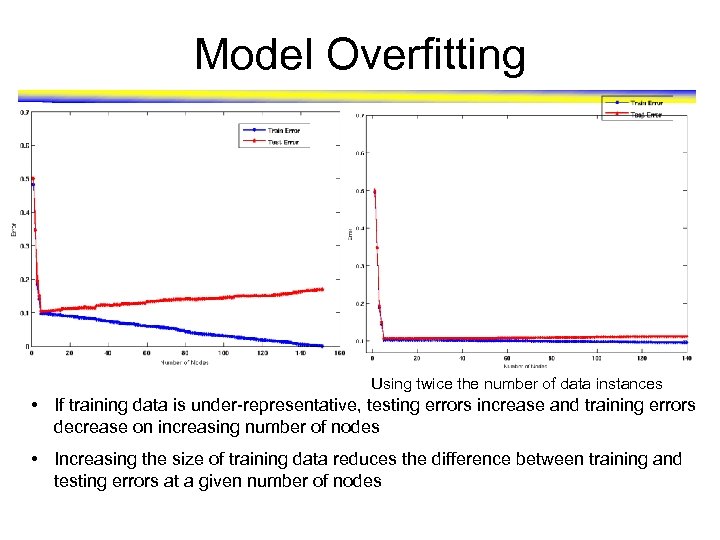
Model Overfitting Using twice the number of data instances • If training data is under-representative, testing errors increase and training errors decrease on increasing number of nodes • Increasing the size of training data reduces the difference between training and testing errors at a given number of nodes

Reasons for Model Overfitting • Lack of Representative Samples • Model is too complex – Multiple comparisons

Effect of Multiple Comparison Procedure • Consider the task of predicting whether stock market will rise/fall in the next 10 trading days • Make 10 random guesses in a row: Up Day 2 Down Day 3 Down Day 4 Up Day 5 Down Day 6 Down Day 7 • Random guessing: P(correct) = 0. 5 Day 1 Up Day 8 Up Day 9 Up Day 10 Down

Effect of Multiple Comparison Procedure • Approach: – Get 50 analysts – Each analyst makes 10 random guesses – Choose the analyst that makes the most number of correct predictions • Probability that at least one analyst makes at least 8 correct predictions

Effect of Multiple Comparison Procedure • Many algorithms employ the following greedy strategy: – Initial model: M – Alternative model: M’ = M , where is a component to be added to the model (e. g. , a test condition of a decision tree) – Keep M’ if improvement, (M, M’) > • Often times, is chosen from a set of alternative components, = { 1, 2, …, k} • If many alternatives are available, one may inadvertently add irrelevant components to the model, resulting in model overfitting
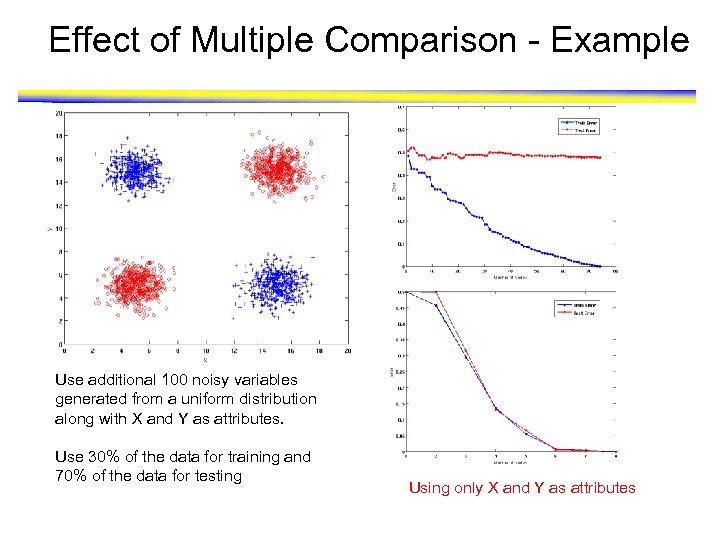
Effect of Multiple Comparison - Example Use additional 100 noisy variables generated from a uniform distribution along with X and Y as attributes. Use 30% of the data for training and 70% of the data for testing Using only X and Y as attributes

Notes on Overfitting • Overfitting results in decision trees that are more complex than necessary • Training error does not provide a good estimate of how well the tree will perform on previously unseen records • Need ways for incorporating model complexity into model development

Evaluating Performance of Classifier • Model Selection – Performed during model building – Purpose is to ensure that model is not overly complex (to avoid overfitting) • Model Evaluation – Performed after model has been constructed – Purpose is to estimate performance of classifier on previously unseen data (e. g. , test set)

Methods for Classifier Evaluation • Holdout – Reserve k% for training and (100 -k)% for testing • Random subsampling – Repeated holdout • Cross validation – Partition data into k disjoint subsets – k-fold: train on k-1 partitions, test on the remaining one – Leave-one-out: k=n • Bootstrap – Sampling with replacement –. 632 bootstrap:

Application on Biomedical Data
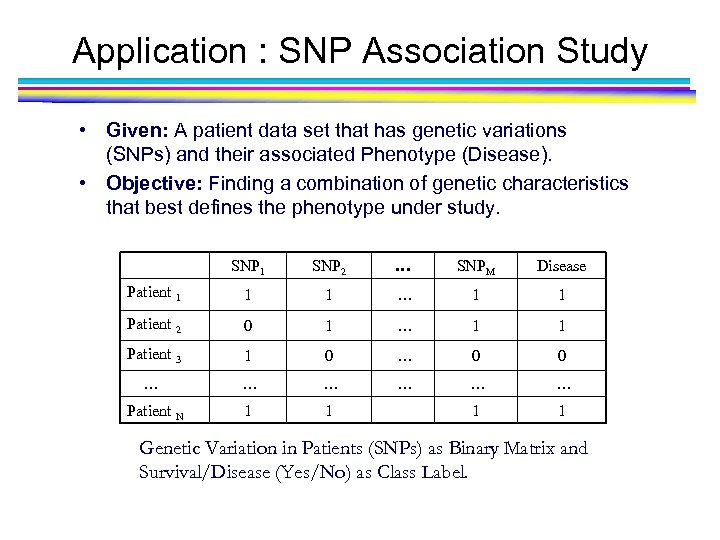
Application : SNP Association Study • Given: A patient data set that has genetic variations (SNPs) and their associated Phenotype (Disease). • Objective: Finding a combination of genetic characteristics that best defines the phenotype under study. SNP 1 SNP 2 … SNPM Disease Patient 1 1 1 … 1 1 Patient 2 0 1 … 1 1 Patient 3 1 0 … 0 0 … … … Patient N 1 1 Genetic Variation in Patients (SNPs) as Binary Matrix and Survival/Disease (Yes/No) as Class Label.

SNP (Single nucleotide polymorphism) • Definition of SNP (wikipedia) – A SNP is defined as a single base change in a DNA sequence that occurs in a significant proportion (more than 1 percent) of a large population Individual 1 Individual 2 Individual 3 Individual 4 Individual 5 AGCGTGA AGCGTGA TCGAGGCTA GCGAGGCTA TCGAGGCTA Each SNP has 3 values ( GG / GT / TT ) ( mm / Mm/ MM) SNP – How many SNPs in Human genome? – 10, 000

Why is SNPs interesting? • In human beings, 99. 9 percent bases are same. • Remaining 0. 1 percent makes a person unique. – Different attributes / characteristics / traits • how a person looks, • diseases a person develops. • These variations can be: – Harmless (change in phenotype) – Harmful (diabetes, cancer, heart disease, Huntington's disease, and hemophilia ) – Latent (variations found in coding and regulatory regions, are not harmful on their own, and the change in each gene only becomes apparent under certain conditions e. g. susceptibility to lung cancer)

Issues in SNP Association Study • In disease association studies number of SNPs varies from a small number (targeted study) to a million (GWA Studies) • Number of samples is usually small • Data sets may have noise or missing values. • Phenotype definition is not trivial (ex. definition of survival) • Environmental exposure, food habits etc adds more variability even among individuals defined under the same phenotype • Genetic heterogeneity among individuals for the same phenotype

Existing Analysis Methods • Univariate Analysis: single SNP tested against the phenotype for correlaton and ranked. – Feasible but doesn’t capture the existing true combinations. • Multivariate Analysis: groups of SNPs of size two or more are tested for possible association with the phenotype. – Infeasible but captures any true combinations. • These two approaches are used to identify biomarkers. • Some approaches employ classification methods like SVMs to classify cases and controls.
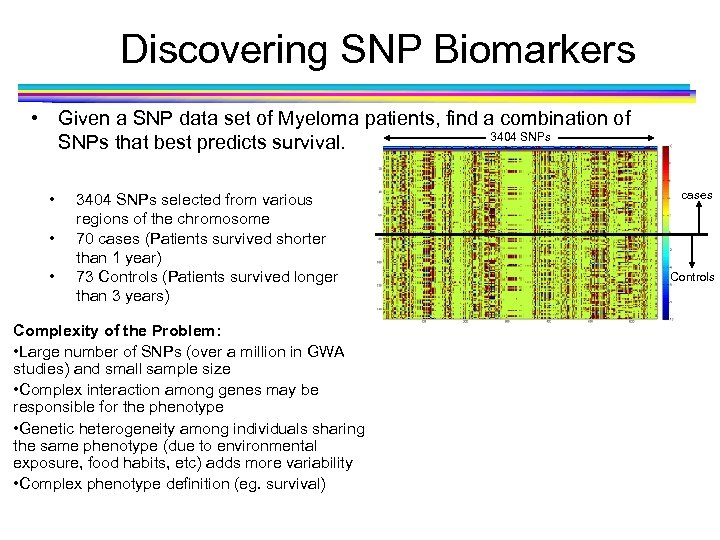
Discovering SNP Biomarkers • Given a SNP data set of Myeloma patients, find a combination of 3404 SNPs that best predicts survival. • • • 3404 SNPs selected from various regions of the chromosome 70 cases (Patients survived shorter than 1 year) 73 Controls (Patients survived longer than 3 years) Complexity of the Problem: • Large number of SNPs (over a million in GWA studies) and small sample size • Complex interaction among genes may be responsible for the phenotype • Genetic heterogeneity among individuals sharing the same phenotype (due to environmental exposure, food habits, etc) adds more variability • Complex phenotype definition (eg. survival) cases Controls

Discovering SNP Biomarkers • Given a SNP data set of Myeloma patients, find a combination of 3404 SNPs that best predicts survival. • • • cases 3404 SNPs selected from various regions of the chromosome 70 cases (Patients survived shorter than 1 year) 73 Controls (Patients survived longer than 3 years) Controls Odds ratio Measures whether two groups have the same odds of an event. OR = 1 Odds of event is equal in both groups OR > 1 Odds of event is higher in cases OR < 1 Odds of event is higher in controls Biomarker (SNPs) Has Marker Lacks Marker Odds ratio is invariant to row and column scaling CASE a b Control CLASS c d
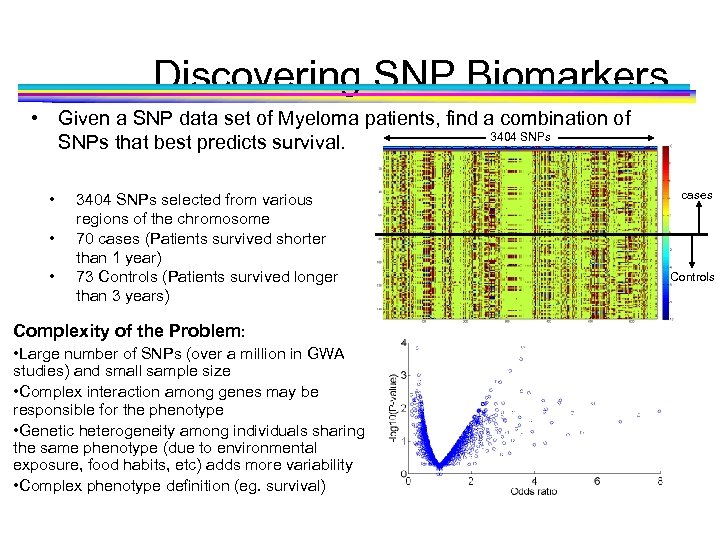
Discovering SNP Biomarkers • Given a SNP data set of Myeloma patients, find a combination of 3404 SNPs that best predicts survival. • • • 3404 SNPs selected from various regions of the chromosome 70 cases (Patients survived shorter than 1 year) 73 Controls (Patients survived longer than 3 years) Complexity of the Problem: • Large number of SNPs (over a million in GWA studies) and small sample size • Complex interaction among genes may be responsible for the phenotype • Genetic heterogeneity among individuals sharing the same phenotype (due to environmental exposure, food habits, etc) adds more variability • Complex phenotype definition (eg. survival) cases Controls

P-value • P-value – Statistical terminology for a probability value – Is the probability that the we get an odds ratio as extreme as the one we got by random chance – Computed by using the chi-square statistic or Fisher’s exact test • Chi-square statistic is not valid if the number of entries in a cell of the contingency table is small • p-value = 1 – hygecdf( a – 1, a+b+c+d, a+c, a+b ) if we are testing value is higher than expected by random chance using Fisher’s exact test • A statistical test to determine if there are nonrandom associations between two categorical variables. – P-values are often expressed in terms of the negative log of p-value, e. g. , -log 10(0. 005) = 2. 3 54
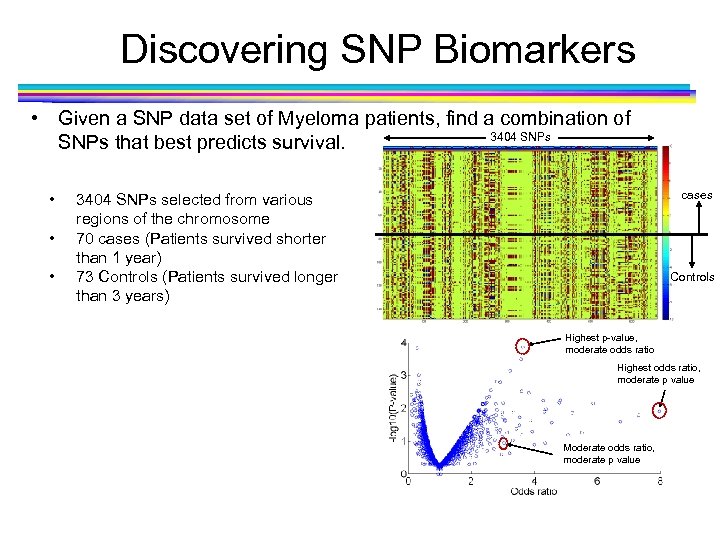
Discovering SNP Biomarkers • Given a SNP data set of Myeloma patients, find a combination of 3404 SNPs that best predicts survival. • • • cases 3404 SNPs selected from various regions of the chromosome 70 cases (Patients survived shorter than 1 year) 73 Controls (Patients survived longer than 3 years) Controls Highest p-value, moderate odds ratio Highest odds ratio, moderate p value Moderate odds ratio, moderate p value
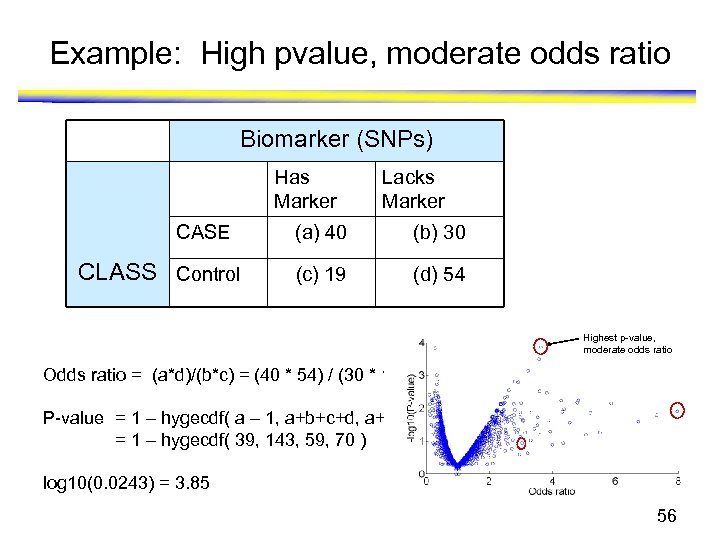
Example: High pvalue, moderate odds ratio Biomarker (SNPs) Has Marker CASE CLASS Control Lacks Marker (a) 40 (b) 30 (c) 19 (d) 54 Highest p-value, moderate odds ratio Odds ratio = (a*d)/(b*c) = (40 * 54) / (30 * 19) = 3. 64 P-value = 1 – hygecdf( a – 1, a+b+c+d, a+c, a+b ) = 1 – hygecdf( 39, 143, 59, 70 ) log 10(0. 0243) = 3. 85 56
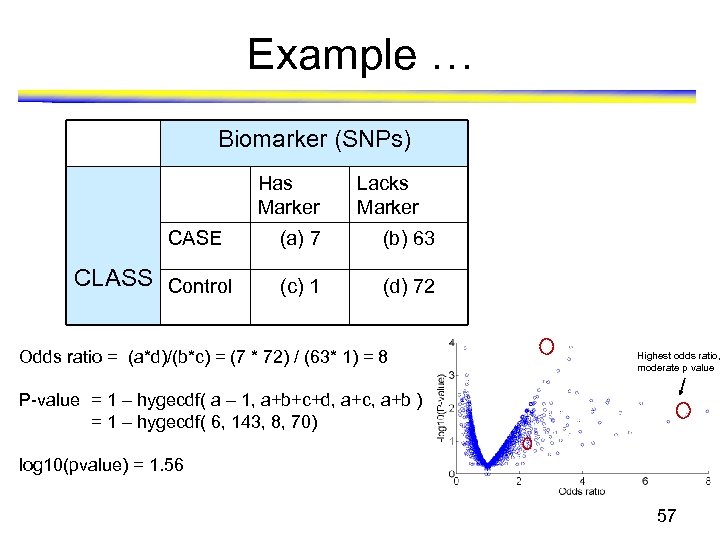
Example … Biomarker (SNPs) Has Marker CASE CLASS Control Lacks Marker (a) 7 (b) 63 (c) 1 (d) 72 Odds ratio = (a*d)/(b*c) = (7 * 72) / (63* 1) = 8 Highest odds ratio, moderate p value P-value = 1 – hygecdf( a – 1, a+b+c+d, a+c, a+b ) = 1 – hygecdf( 6, 143, 8, 70) log 10(pvalue) = 1. 56 57
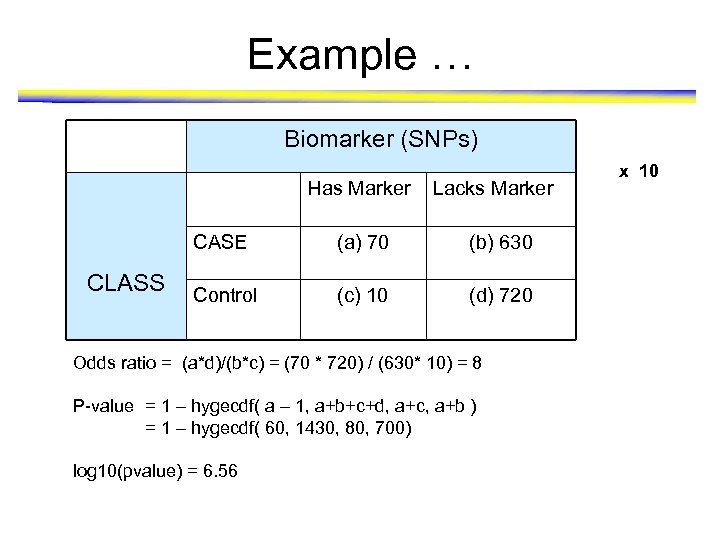
Example … Biomarker (SNPs) Has Marker Lacks Marker CASE CLASS (a) 70 (b) 630 Control (c) 10 (d) 720 Odds ratio = (a*d)/(b*c) = (70 * 720) / (630* 10) = 8 P-value = 1 – hygecdf( a – 1, a+b+c+d, a+c, a+b ) = 1 – hygecdf( 60, 1430, 80, 700) log 10(pvalue) = 6. 56 x 10
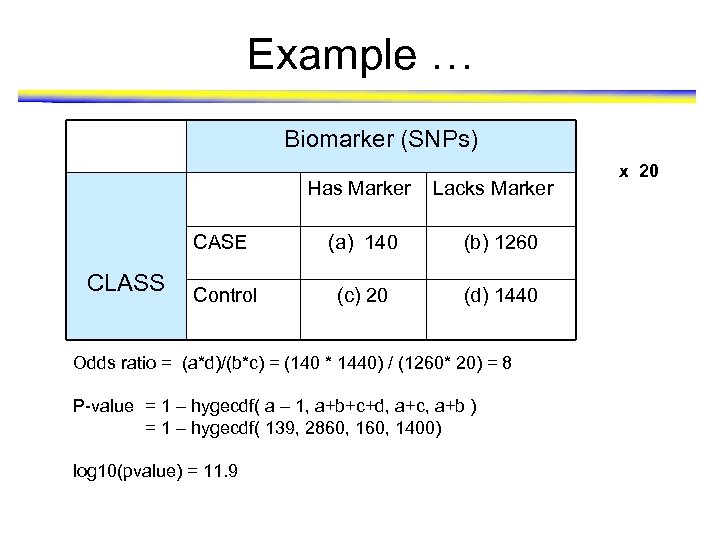
Example … Biomarker (SNPs) Has Marker Lacks Marker CASE CLASS (a) 140 (b) 1260 Control (c) 20 (d) 1440 Odds ratio = (a*d)/(b*c) = (140 * 1440) / (1260* 20) = 8 P-value = 1 – hygecdf( a – 1, a+b+c+d, a+c, a+b ) = 1 – hygecdf( 139, 2860, 1400) log 10(pvalue) = 11. 9 x 20
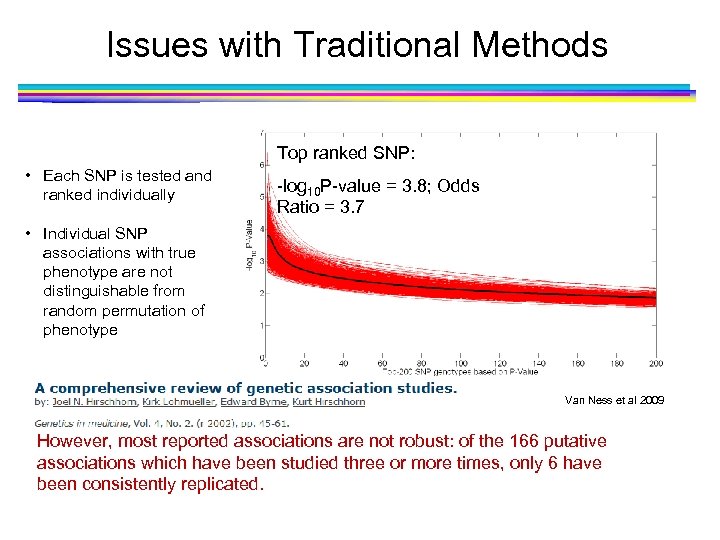
Issues with Traditional Methods Top ranked SNP: • Each SNP is tested and ranked individually -log 10 P-value = 3. 8; Odds Ratio = 3. 7 • Individual SNP associations with true phenotype are not distinguishable from random permutation of phenotype Van Ness et al 2009 However, most reported associations are not robust: of the 166 putative associations which have been studied three or more times, only 6 have been consistently replicated.
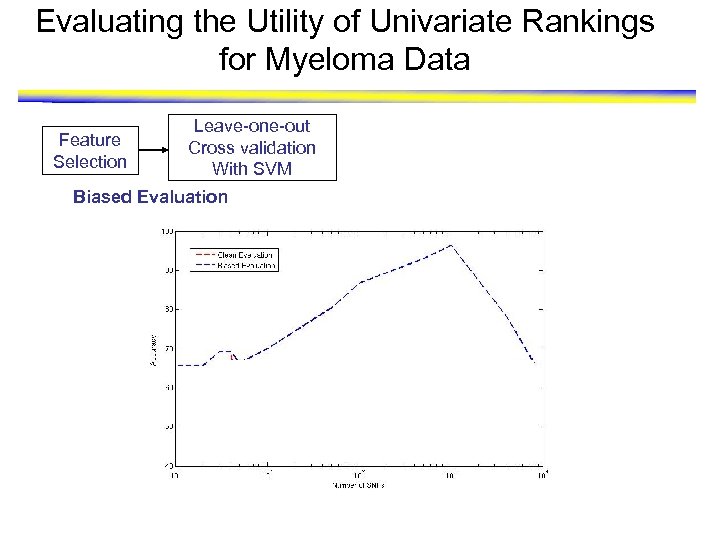
Evaluating the Utility of Univariate Rankings for Myeloma Data Feature Selection Leave-one-out Cross validation With SVM Biased Evaluation
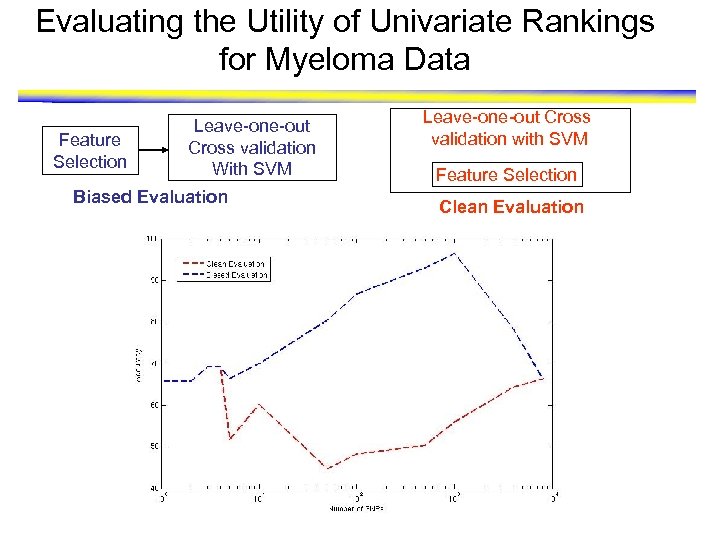
Evaluating the Utility of Univariate Rankings for Myeloma Data Feature Selection Leave-one-out Cross validation With SVM Biased Evaluation Leave-one-out Cross validation with SVM Feature Selection Clean Evaluation
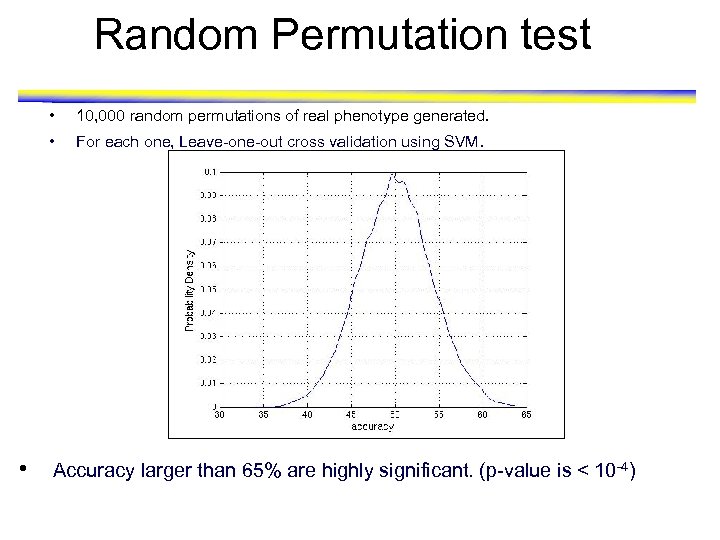
Random Permutation test • • • 10, 000 random permutations of real phenotype generated. For each one, Leave-one-out cross validation using SVM. Accuracy larger than 65% are highly significant. (p-value is < 10 -4)

Clustering
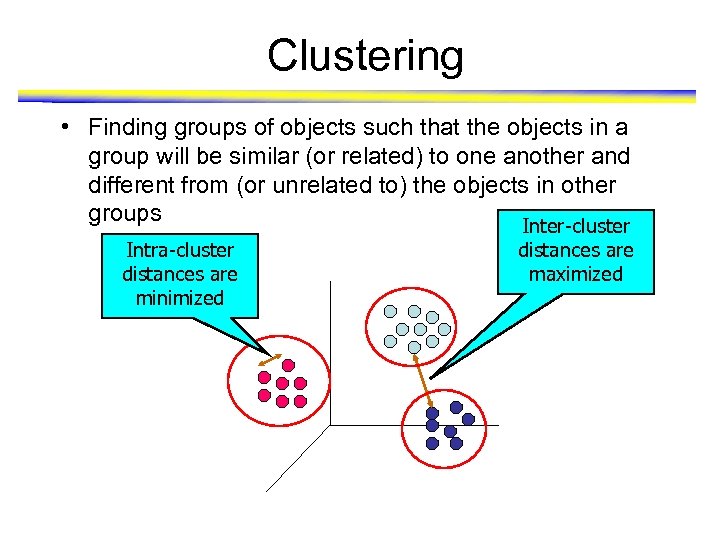
Clustering • Finding groups of objects such that the objects in a group will be similar (or related) to one another and different from (or unrelated to) the objects in other groups Inter-cluster Intra-cluster distances are minimized distances are maximized

Applications of Clustering • Applications: – Gene expression clustering – Clustering of patients based on phenotypic and genotypic factors for efficient disease diagnosis – Market Segmentation – Document Clustering – Finding groups of driver behaviors based upon patterns of automobile motions (normal, drunken, sleepy, rush hour driving, etc) Courtesy: Michael Eisen
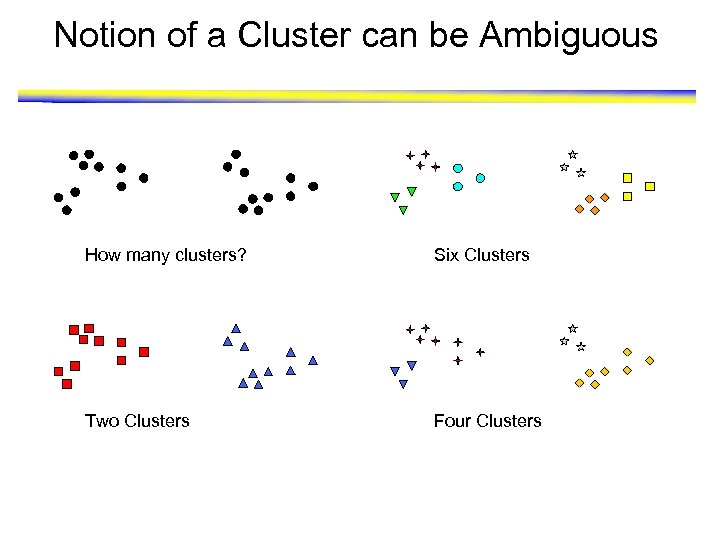
Notion of a Cluster can be Ambiguous How many clusters? Six Clusters Two Clusters Four Clusters

Similarity and Dissimilarity Measures • Similarity measure – Numerical measure of how alike two data objects are. – Is higher when objects are more alike. – Often falls in the range [0, 1] • Dissimilarity measure – Numerical measure of how different are two data objects – Lower when objects are more alike – Minimum dissimilarity is often 0 – Upper limit varies • Proximity refers to a similarity or dissimilarity

Euclidean Distance • Euclidean Distance Where n is the number of dimensions (attributes) and xk and yk are, respectively, the kth attributes (components) or data objects x and y. • Correlation

Types of Clusterings • A clustering is a set of clusters • Important distinction between hierarchical and partitional sets of clusters • Partitional Clustering – A division data objects into non-overlapping subsets (clusters) such that each data object is in exactly one subset • Hierarchical clustering – A set of nested clusters organized as a hierarchical tree

Other Distinctions Between Sets of Clusters • Exclusive versus non-exclusive – In non-exclusive clusterings, points may belong to multiple clusters. – Can represent multiple classes or ‘border’ points • Fuzzy versus non-fuzzy – In fuzzy clustering, a point belongs to every cluster with some weight between 0 and 1 – Weights must sum to 1 – Probabilistic clustering has similar characteristics • Partial versus complete – In some cases, we only want to cluster some of the data • Heterogeneous versus homogeneous – Clusters of widely different sizes, shapes, and densities

Clustering Algorithms • K-means and its variants • Hierarchical clustering • Other types of clustering

K-means Clustering • • • Partitional clustering approach Number of clusters, K, must be specified Each cluster is associated with a centroid (center point) Each point is assigned to the cluster with the closest centroid The basic algorithm is very simple
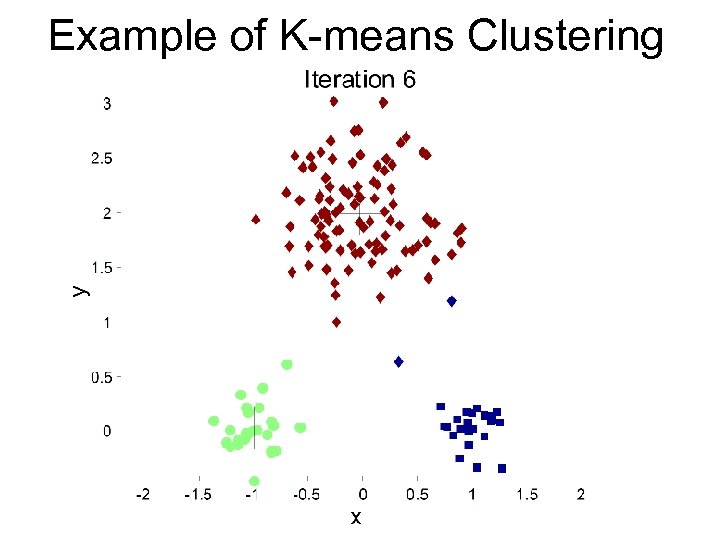
Example of K-means Clustering

K-means Clustering – Details • The centroid is (typically) the mean of the points in the cluster • Initial centroids are often chosen randomly – Clusters produced vary from one run to another • ‘Closeness’ is measured by Euclidean distance, cosine similarity, correlation, etc • Complexity is O( n * K * I * d ) – n = number of points, K = number of clusters, I = number of iterations, d = number of attributes

Evaluating K-means Clusters • Most common measure is Sum of Squared Error (SSE) – For each point, the error is the distance to the nearest cluster – To get SSE, we square these errors and sum them • x is a data point in cluster Ci and mi is the representative point for cluster Ci – Given two sets of clusters, we prefer the one with the smallest error – One easy way to reduce SSE is to increase K, the number of clusters
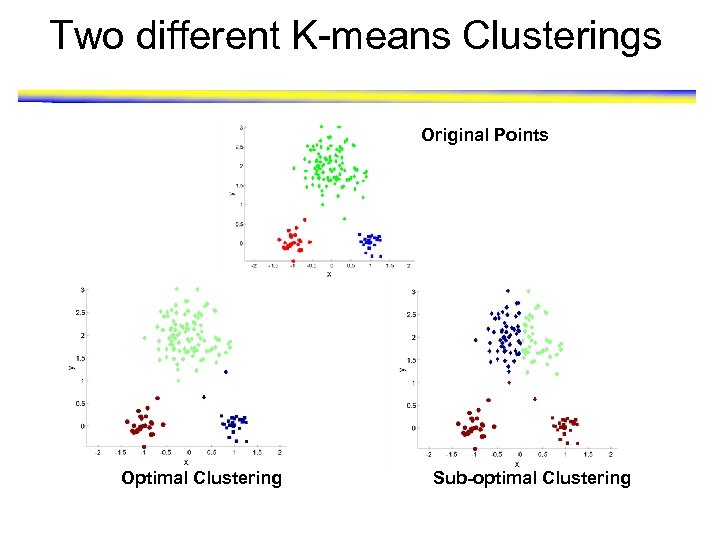
Two different K-means Clusterings Original Points Optimal Clustering Sub-optimal Clustering

Limitations of K-means • K-means has problems when clusters are of differing – Sizes – Densities – Non-globular shapes • K-means has problems when the data contains outliers.
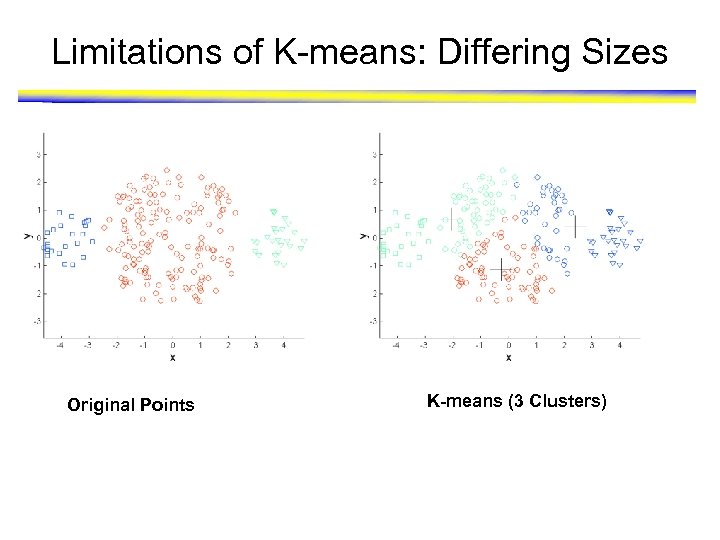
Limitations of K-means: Differing Sizes Original Points K-means (3 Clusters)
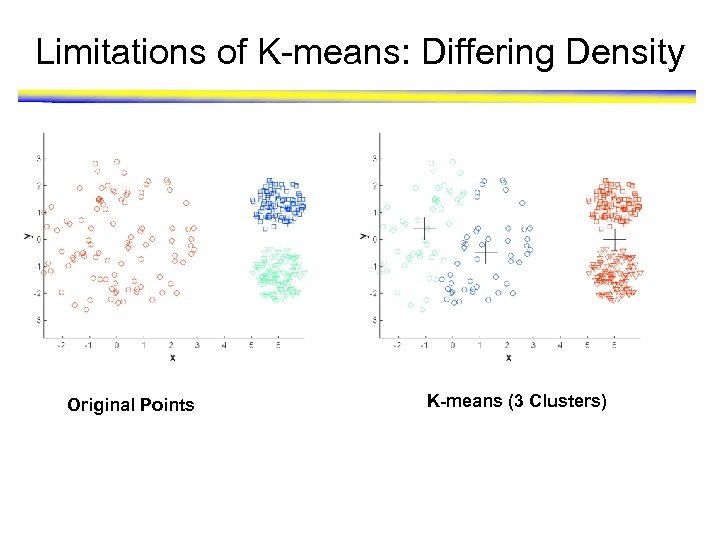
Limitations of K-means: Differing Density Original Points K-means (3 Clusters)
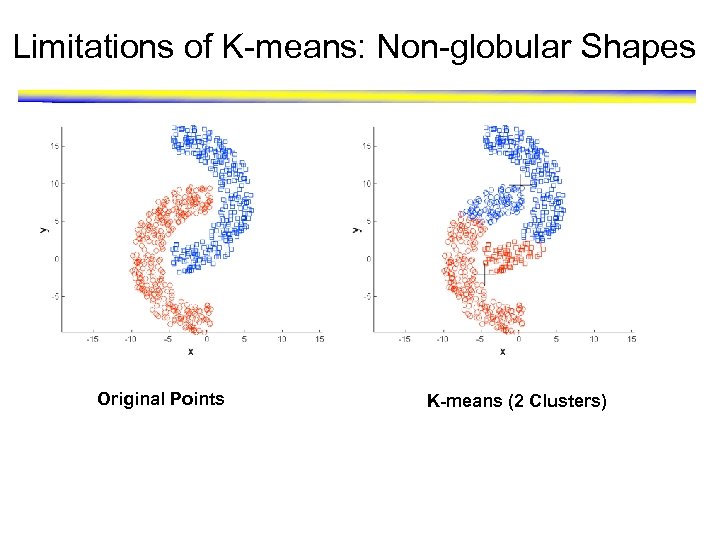
Limitations of K-means: Non-globular Shapes Original Points K-means (2 Clusters)
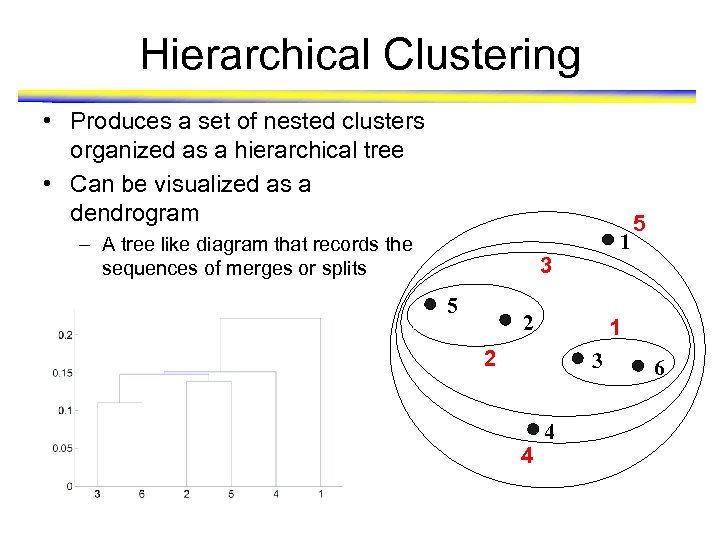
Hierarchical Clustering • Produces a set of nested clusters organized as a hierarchical tree • Can be visualized as a dendrogram – A tree like diagram that records the sequences of merges or splits 1 3 5 2 1 2 3 4 5 4 6

Strengths of Hierarchical Clustering • Do not have to assume any particular number of clusters – Any desired number of clusters can be obtained by ‘cutting’ the dendrogram at the proper level • They may correspond to meaningful taxonomies – Example in biological sciences (e. g. , animal kingdom, phylogeny reconstruction, …)

Hierarchical Clustering • Two main types of hierarchical clustering – Agglomerative: • Start with the points as individual clusters • At each step, merge the closest pair of clusters until only one cluster (or k clusters) left – Divisive: • Start with one, all-inclusive cluster • At each step, split a cluster until each cluster contains a point (or there are k clusters) • Traditional hierarchical algorithms use a similarity or distance matrix – Merge or split one cluster at a time

Agglomerative Clustering Algorithm • More popular hierarchical clustering technique • Basic algorithm is straightforward 1. 2. 3. 4. 5. 6. • Compute the proximity matrix Let each data point be a cluster Repeat Merge the two closest clusters Update the proximity matrix Until only a single cluster remains Key operation is the computation of the proximity of two clusters – Different approaches to defining the distance between clusters distinguish the different algorithms
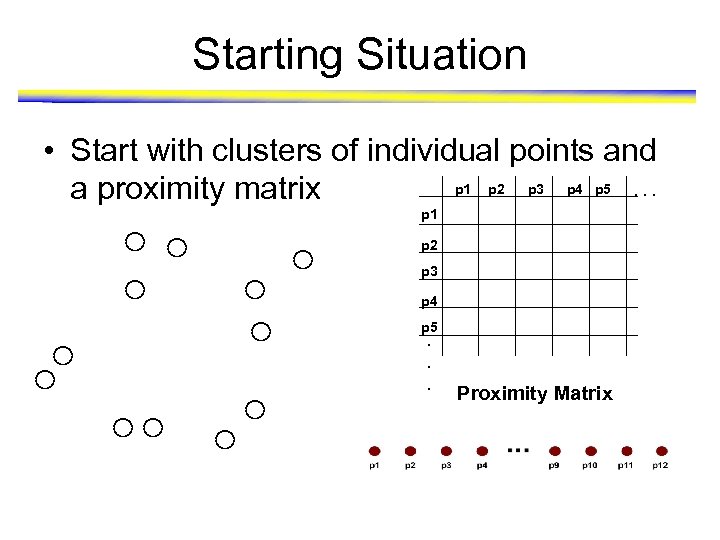
Starting Situation • Start with clusters of individual points and p 1 p 2 p 3 p 4 p 5. . . a proximity matrix p 1 p 2 p 3 p 4 p 5. . . Proximity Matrix
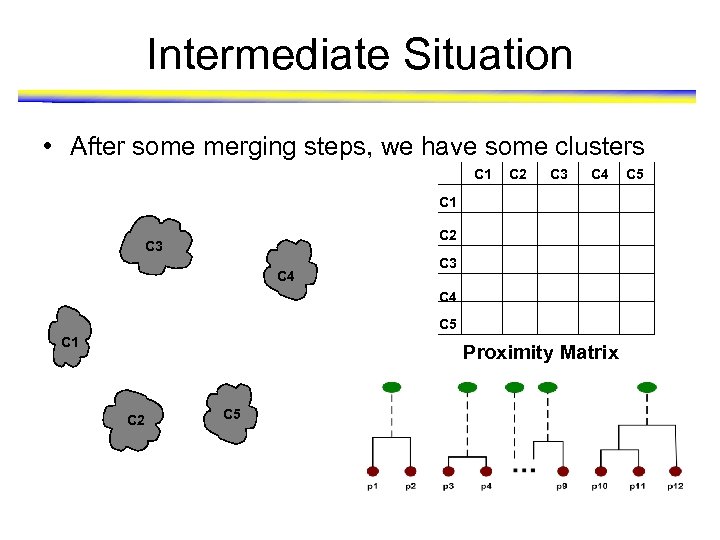
Intermediate Situation • After some merging steps, we have some clusters C 1 C 2 C 3 C 4 C 5 C 1 Proximity Matrix C 2 C 5
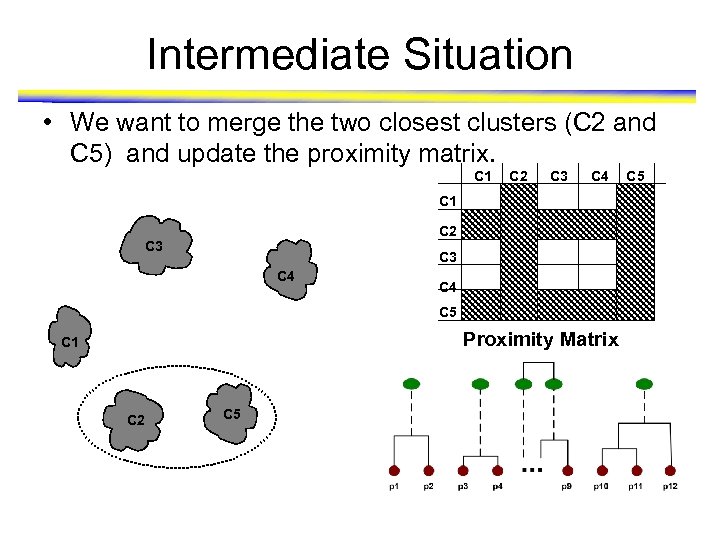
Intermediate Situation • We want to merge the two closest clusters (C 2 and C 5) and update the proximity matrix. C 1 C 2 C 3 C 4 C 5 Proximity Matrix C 1 C 2 C 5
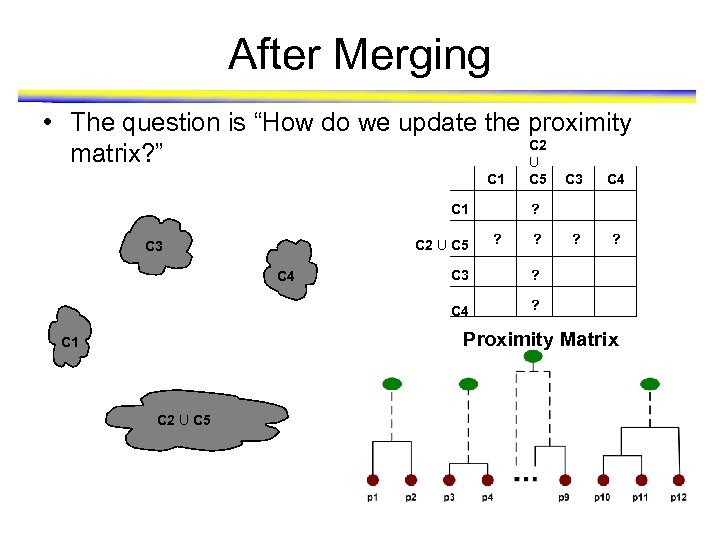
After Merging • The question is “How do we update the proximity C 2 matrix? ” U C 1 C 2 U C 5 C 3 C 5 C 4 ? ? ? C 3 ? C 4 C 3 ? Proximity Matrix C 1 C 2 U C 5
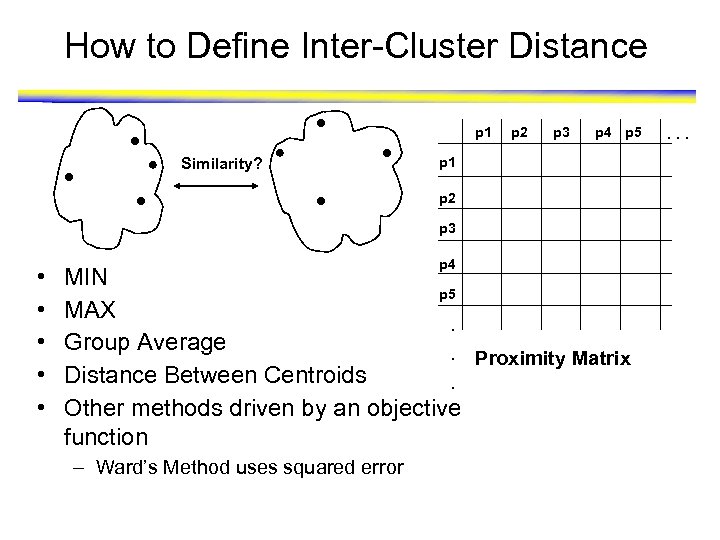
How to Define Inter-Cluster Distance p 1 Similarity? p 2 p 3 p 4 p 5 p 1 p 2 p 3 • • • p 4 MIN p 5 MAX. Group Average. Proximity Matrix Distance Between Centroids. Other methods driven by an objective function – Ward’s Method uses squared error . . .
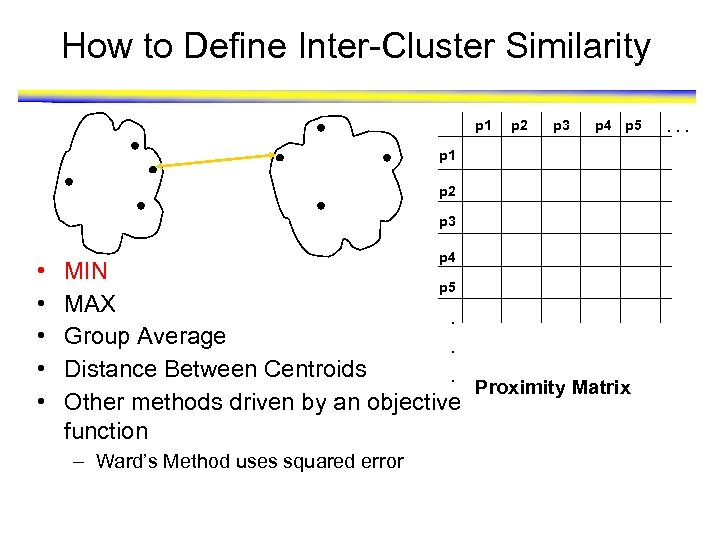
How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 • • • p 4 MIN p 5 MAX. Group Average. Distance Between Centroids. Proximity Matrix Other methods driven by an objective function – Ward’s Method uses squared error . . .
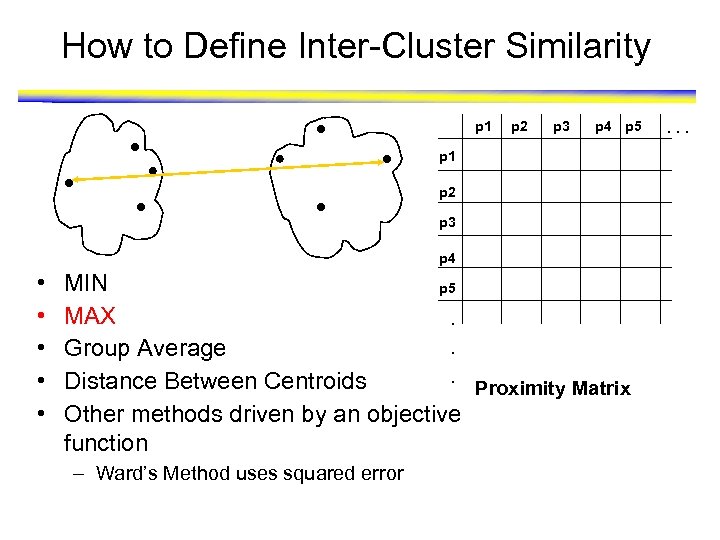
How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 • • • MIN p 5 MAX. . Group Average. Distance Between Centroids Proximity Matrix Other methods driven by an objective function – Ward’s Method uses squared error . . .
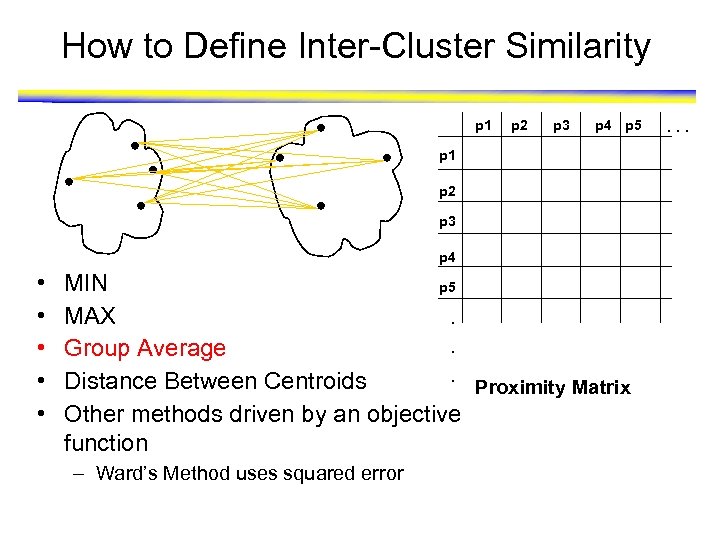
How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 • • • MIN p 5 MAX. . Group Average. Distance Between Centroids Proximity Matrix Other methods driven by an objective function – Ward’s Method uses squared error . . .
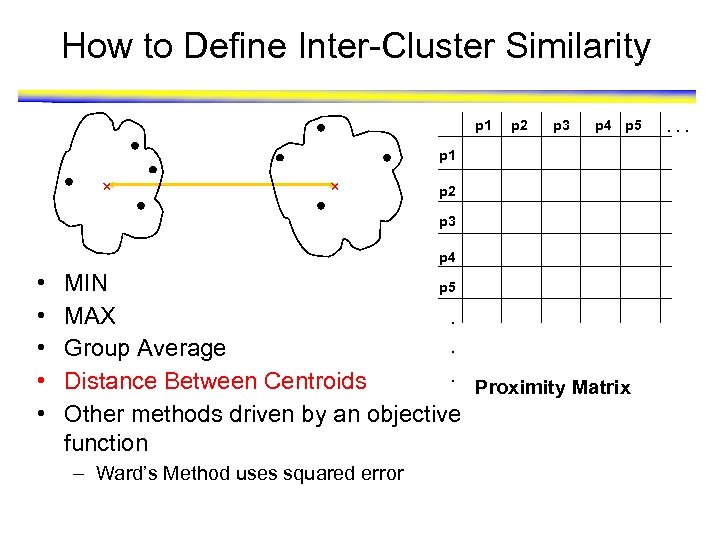
How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 • • • MIN p 5 MAX. . Group Average. Distance Between Centroids Proximity Matrix Other methods driven by an objective function – Ward’s Method uses squared error . . .

Other Types of Cluster Algorithms • Hundreds of clustering algorithms • Some clustering algorithms – K-means – Hierarchical – Statistically based clustering algorithms • Mixture model based clustering – Fuzzy clustering – Self-organizing Maps (SOM) – Density-based (DBSCAN) • Proper choice of algorithms depends on the type of clusters to be found, the type of data, and the objective

Cluster Validity • For supervised classification we have a variety of measures to evaluate how good our model is – Accuracy, precision, recall • For cluster analysis, the analogous question is how to evaluate the “goodness” of the resulting clusters? • But “clusters are in the eye of the beholder”! • Then why do we want to evaluate them? – – To avoid finding patterns in noise To compare clustering algorithms To compare two sets of clusters To compare two clusters
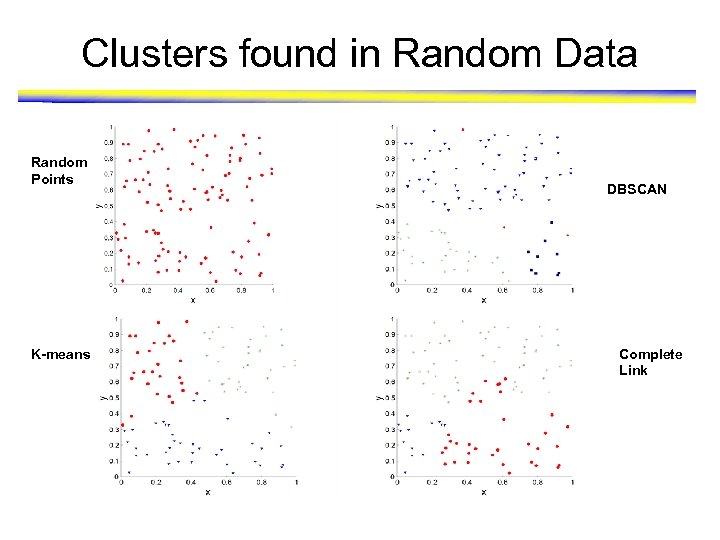
Clusters found in Random Data Random Points K-means DBSCAN Complete Link

Different Aspects of Cluster Validation • Distinguishing whether non-random structure actually exists in the data • Comparing the results of a cluster analysis to externally known results, e. g. , to externally given class labels • Evaluating how well the results of a cluster analysis fit the data without reference to external information • Comparing the results of two different sets of cluster analyses to determine which is better • Determining the ‘correct’ number of clusters
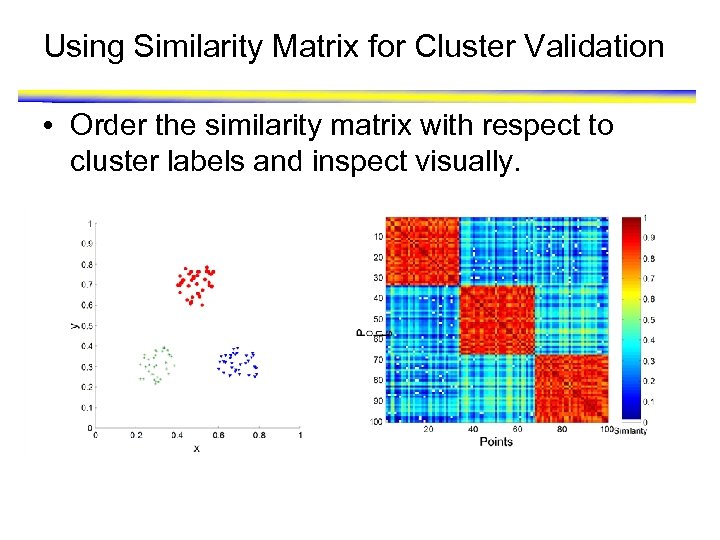
Using Similarity Matrix for Cluster Validation • Order the similarity matrix with respect to cluster labels and inspect visually.
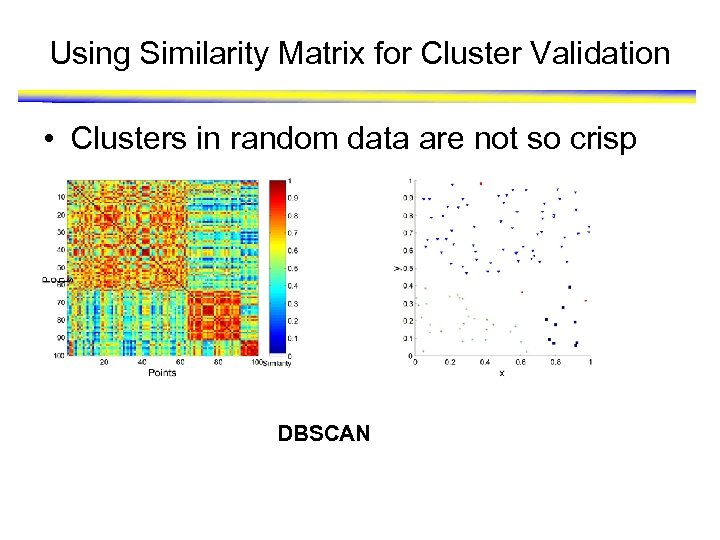
Using Similarity Matrix for Cluster Validation • Clusters in random data are not so crisp DBSCAN
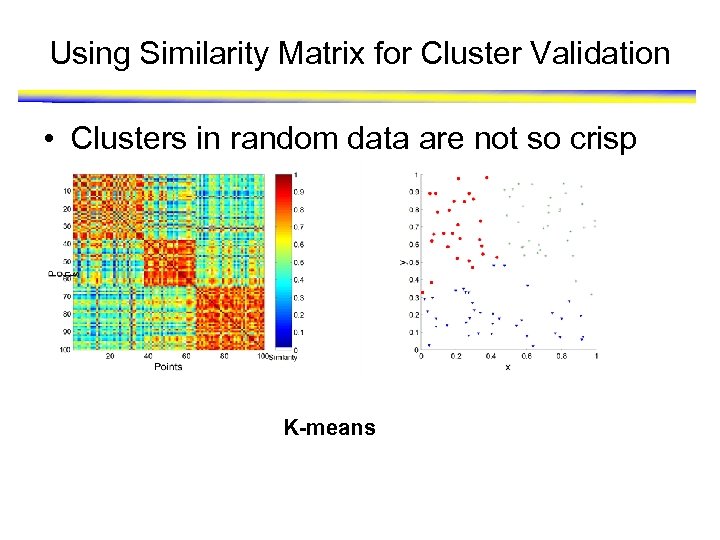
Using Similarity Matrix for Cluster Validation • Clusters in random data are not so crisp K-means
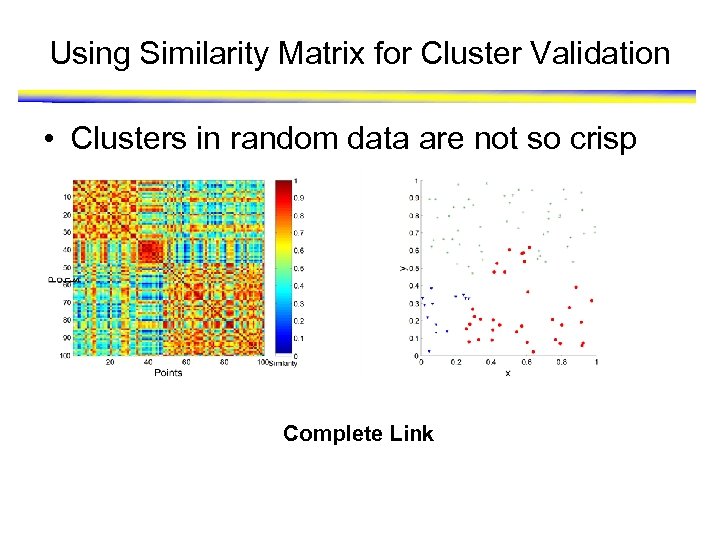
Using Similarity Matrix for Cluster Validation • Clusters in random data are not so crisp Complete Link

Measures of Cluster Validity • Numerical measures that are applied to judge various aspects of cluster validity, are classified into the following three types of indices. – External Index: Used to measure the extent to which cluster labels match externally supplied class labels. • Entropy – Internal Index: Used to measure the goodness of a clustering structure without respect to external information. • Sum of Squared Error (SSE) – Relative Index: Used to compare two different clusterings or clusters. • Often an external or internal index is used for this function, e. g. , SSE or entropy • For futher details please see “Introduction to Data Mining”, Chapter 8. – http: //www-users. cs. umn. edu/~kumar/dmbook/ch 8. pdf

Clustering Microarray Data

Clustering Microarray Data • Microarray analysis allows the monitoring of the activities of many genes over many different conditions • Data: Expression profiles of approximately 3606 genes of E Coli are recorded for 30 experimental conditions • SAM (Significance Analysis of Microarrays) package from Stanford University is used for the analysis of the data and to identify the genes that are substantially differentially upregulated in the dataset – 17 such genes are identified for study purposes • Hierarchical clustering is performed and plotted using Tree. View C 1 C 2 C 3 C 4 C 5 C 6 C 7 Gene 1 Gene 2 Gene 3 Gene 4 Gene 5 Gene 6 Gene 7 ….
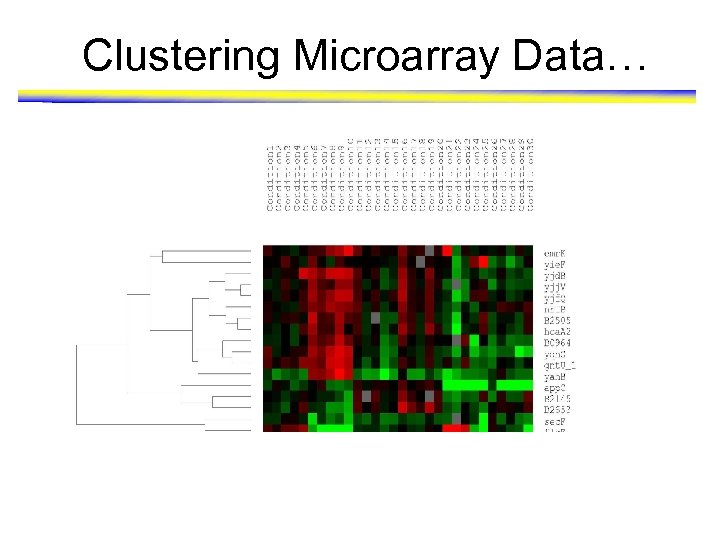
Clustering Microarray Data…
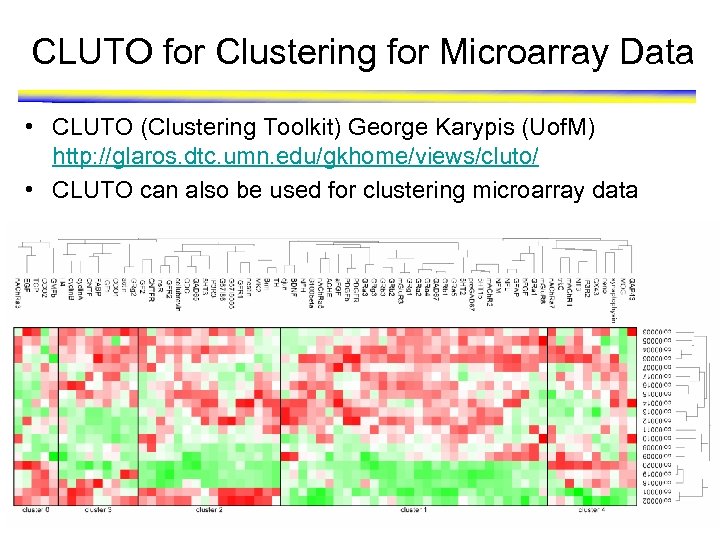
CLUTO for Clustering for Microarray Data • CLUTO (Clustering Toolkit) George Karypis (Uof. M) http: //glaros. dtc. umn. edu/gkhome/views/cluto/ • CLUTO can also be used for clustering microarray data

Issues in Clustering Expression Data • Similarity uses all the conditions – We are typically interested in sets of genes that are similar for a relatively small set of conditions • Most clustering approaches assume that an object can only be in one cluster – A gene may belong to more than one functional group – Thus, overlapping groups are needed • Can either use clustering that takes these factors into account or use other techniques – For example, association analysis

Clustering Packages • Mathematical and Statistical Packages – – MATLAB SAS SPSS R • CLUTO (Clustering Toolkit) George Karypis (UM) http: //glaros. dtc. umn. edu/gkhome/views/cluto/ • Cluster Michael Eisen (LBNL/UCB) (microarray) • http: //rana. lbl. gov/Eisen. Software. htm http: //genome-www 5. stanford. edu/resources/restech. shtml (more microarray clustering algorithms) Many others – KDNuggets http: //www. kdnuggets. com/software/clustering. html

Association Analysis
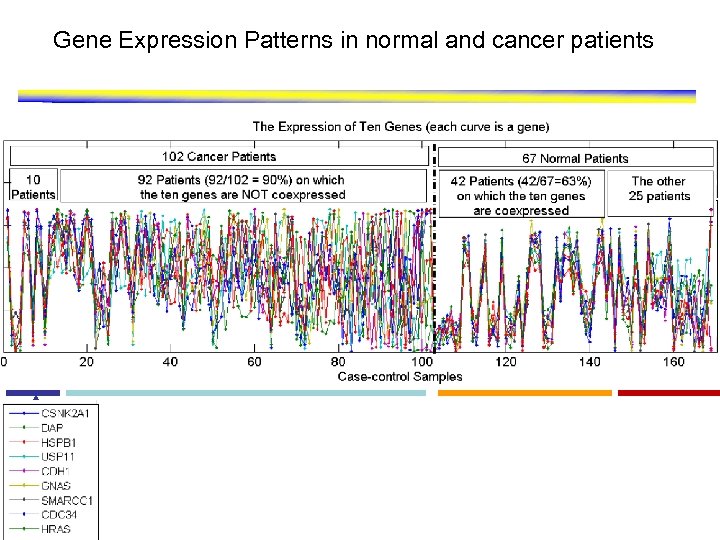
Gene Expression Patterns in normal and cancer patients

Association Analysis • Given a set of records, find dependency rules which will predict occurrence of an item based on occurrences of other items in the record Rules Discovered: {Milk} --> {Coke} (s=0. 6, c=0. 75) {Diaper, Milk} --> {Beer} (s=0. 4, c=0. 67) • Applications – Marketing and Sales Promotion – Supermarket shelf management – Traffic pattern analysis (e. g. , rules such as "high congestion on Intersection 58 implies high accident rates for left turning traffic")

Association Rule Mining Task • Given a set of transactions T, the goal of association rule mining is to find all rules having – support ≥ minsup threshold – confidence ≥ minconf threshold • Brute-force approach: Two Steps – Frequent Itemset Generation • Generate all itemsets whose support minsup – Rule Generation • Generate high confidence rules from each frequent itemset, where each rule is a binary partitioning of a frequent itemset • Frequent itemset generation is computationally expensive
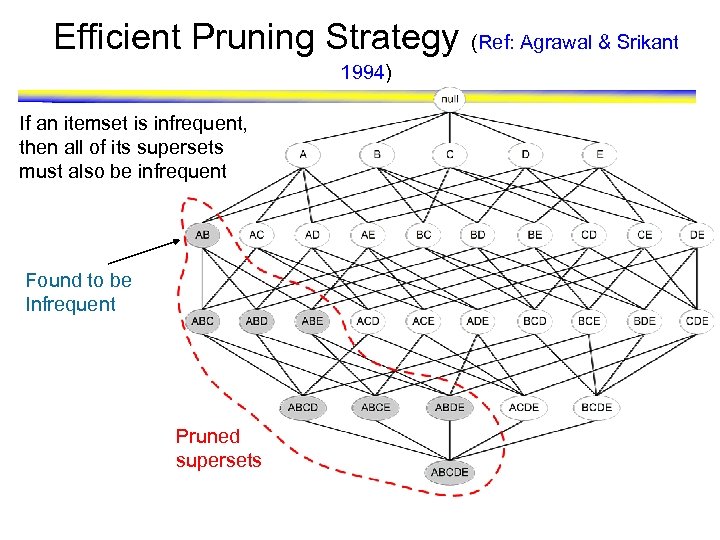
Efficient Pruning Strategy 1994) If an itemset is infrequent, then all of its supersets must also be infrequent Found to be Infrequent Pruned supersets (Ref: Agrawal & Srikant
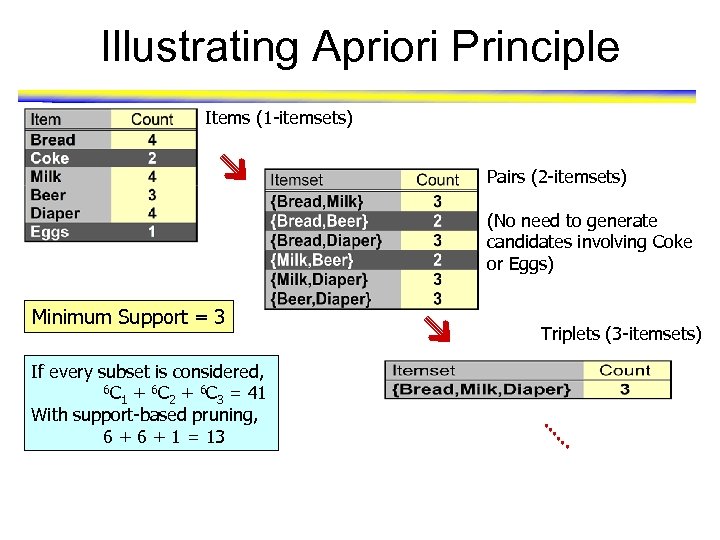
Illustrating Apriori Principle Items (1 -itemsets) Pairs (2 -itemsets) (No need to generate candidates involving Coke or Eggs) Minimum Support = 3 If every subset is considered, 6 C + 6 C = 41 1 2 3 With support-based pruning, 6 + 1 = 13 Triplets (3 -itemsets)

Association Measures • Association measures evaluate the strength of an association pattern – Support and confidence are the most commonly used – The support, (X), of an itemset X is the number of transactions that contain all the items of the itemset • Frequent itemsets have support > specified threshold • Different types of itemset patterns are distinguished by a measure and a threshold – The confidence of an association rule is given by conf(X Y) = (X Y) / (X) • Estimate of the conditional probability of Y given X • Other measures can be more useful – H-confidence – Interest

Application on Biomedical Data
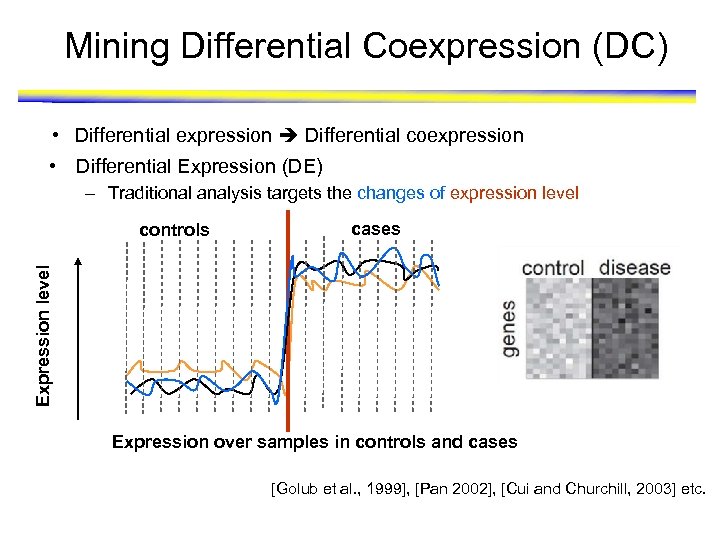
Mining Differential Coexpression (DC) • Differential expression Differential coexpression • Differential Expression (DE) – Traditional analysis targets the changes of expression level cases Expression level controls Expression over samples in controls and cases [Golub et al. , 1999], [Pan 2002], [Cui and Churchill, 2003] etc.
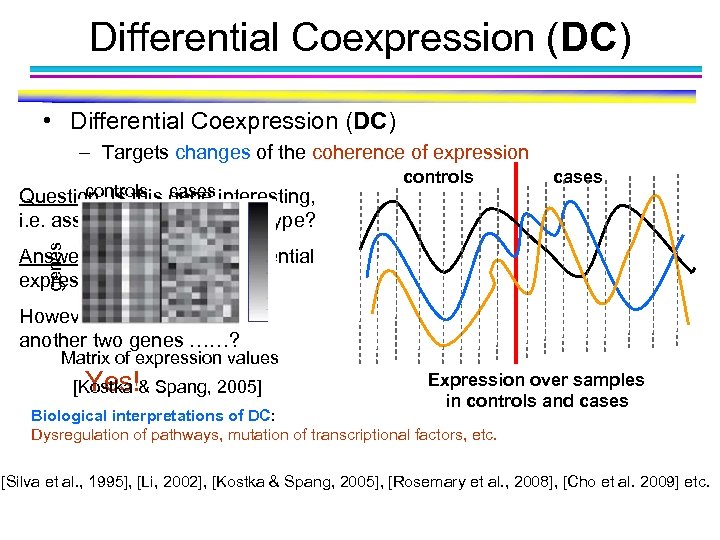
Differential Coexpression (DC) • Differential Coexpression (DC) – Targets changes of the coherence of expression cases genes controls cases Question: Is this gene interesting, i. e. associated w/ the phenotype? controls Answer: No, in term of differential expression (DE). However, what if there another two genes ……? Matrix of expression values Yes! [Kostka & Spang, 2005] Expression over samples in controls and cases Biological interpretations of DC: Dysregulation of pathways, mutation of transcriptional factors, etc. [Silva et al. , 1995], [Li, 2002], [Kostka & Spang, 2005], [Rosemary et al. , 2008], [Cho et al. 2009] etc.

Differential Coexpression (DC) • Existing work on differential coexpression – Pairs of genes with differential coexpression • [Silva et al. , 1995], [Li, 2002], [Li et al. , 2003], [Lai et al. 2004] – Clustering based differential coexpression analysis • [Ihmels et al. , 2005], [Watson. , 2006] – Network based analysis of differential coexpression • [Zhang and Horvath, 2005], [Choi et al. , 2005], [Gargalovic et al. 2006], [Oldham et al. 2006], [Fuller et al. , 2007], [Xu et al. , 2008] – Beyond pair-wise (size-k) differential coexpression • [Kostka and Spang. , 2004], [Prieto et al. , 2006] – Gene-pathway differential coexpression • [Rosemary et al. , 2008] – Pathway-pathway differential coexpression • [Cho et al. , 2009]
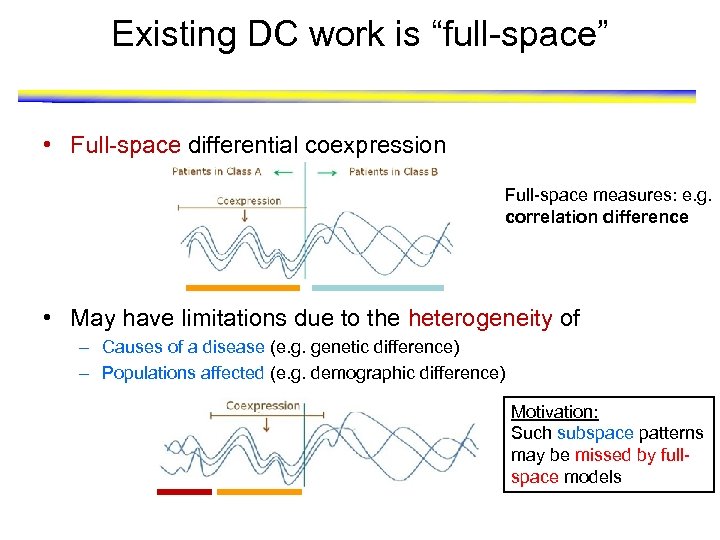
Existing DC work is “full-space” • Full-space differential coexpression Full-space measures: e. g. correlation difference • May have limitations due to the heterogeneity of – Causes of a disease (e. g. genetic difference) – Populations affected (e. g. demographic difference) Motivation: Such subspace patterns may be missed by fullspace models
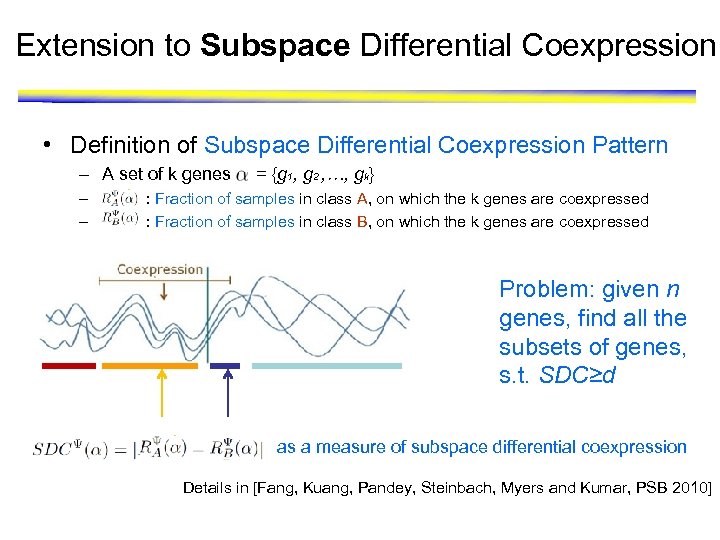
Extension to Subspace Differential Coexpression • Definition of Subspace Differential Coexpression Pattern – A set of k genes – – = {g 1, g 2 , …, gk} : Fraction of samples in class A, on which the k genes are coexpressed : Fraction of samples in class B, on which the k genes are coexpressed Problem: given n genes, find all the subsets of genes, s. t. SDC≥d as a measure of subspace differential coexpression Details in [Fang, Kuang, Pandey, Steinbach, Myers and Kumar, PSB 2010]
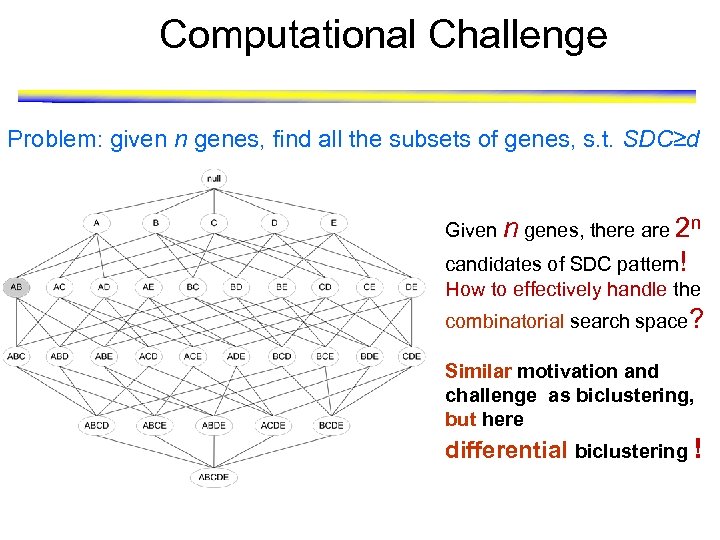
Computational Challenge Problem: given n genes, find all the subsets of genes, s. t. SDC≥d Given n genes, there are 2 n candidates of SDC pattern! How to effectively handle the combinatorial search space? Similar motivation and challenge as biclustering, but here differential biclustering !
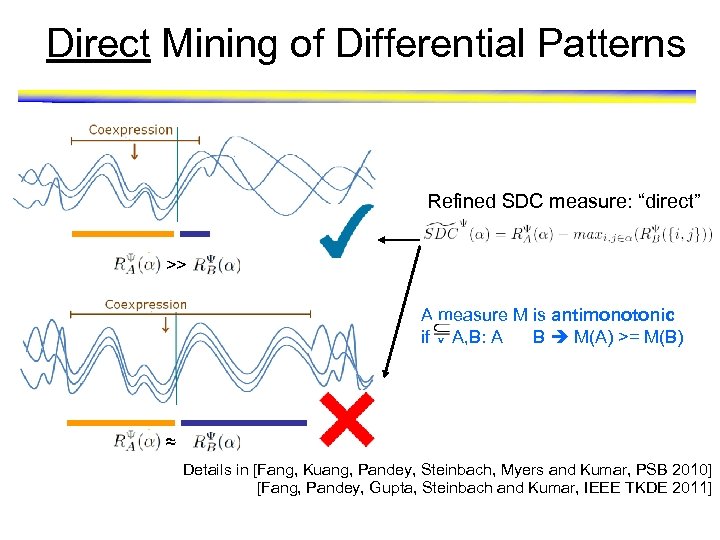
Direct Mining of Differential Patterns Refined SDC measure: “direct” >> A measure M is antimonotonic if V A, B: A B M(A) >= M(B) ≈ Details in [Fang, Kuang, Pandey, Steinbach, Myers and Kumar, PSB 2010] [Fang, Pandey, Gupta, Steinbach and Kumar, IEEE TKDE 2011]
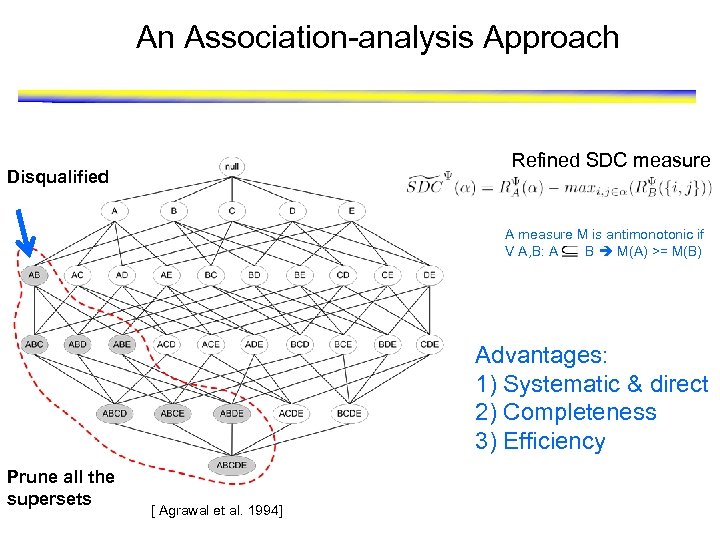
An Association-analysis Approach Refined SDC measure Disqualified A measure M is antimonotonic if V A, B: A B M(A) >= M(B) Advantages: 1) Systematic & direct 2) Completeness 3) Efficiency Prune all the supersets [ Agrawal et al. 1994]
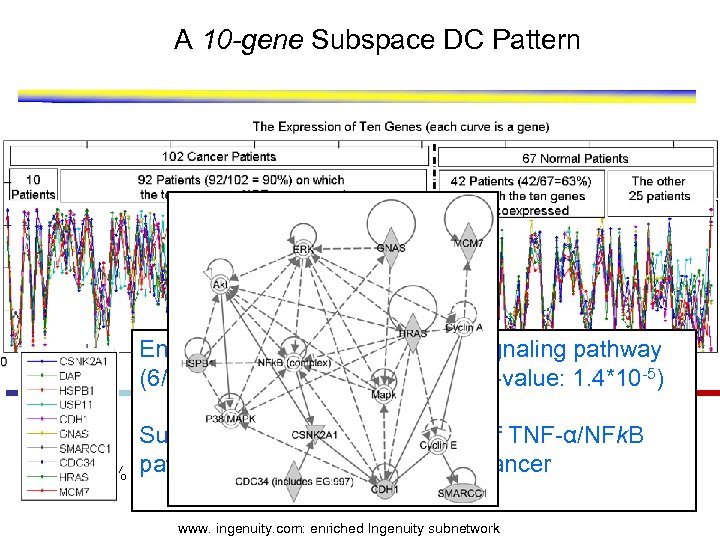
A 10 -gene Subspace DC Pattern Enriched with the TNF-α/NFk. B signaling pathway (6/10 overlap with the pathway, P-value: 1. 4*10 -5) ≈ 10% Suggests that the dysregulation of TNF-α/NFk. B pathway may be related to lung cancer ≈ 60% www. ingenuity. com: enriched Ingenuity subnetwork

Data Mining Book For further details and sample chapters see www. cs. umn. edu/~kumar/dmbook

Case Study 1 Neuroimaging
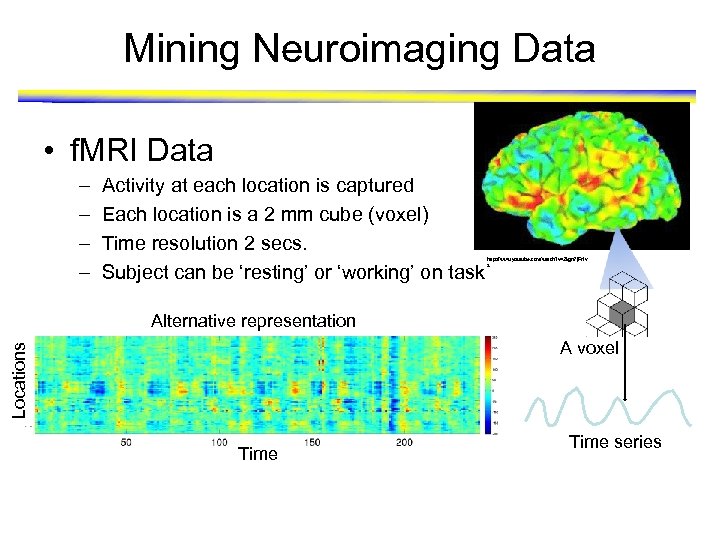
Mining Neuroimaging Data • f. MRI Data – – Activity at each location is captured Each location is a 2 mm cube (voxel) Time resolution 2 secs. Subject can be ‘resting’ or ‘working’ on task http: //www. youtube. com/watch? v=2 kgn 7 j. Ft 1 v s Alternative representation Locations A voxel Time series

Functional Magnetic Resonance Imaging • f. MRI Data Activity at each location is captured Each location is a 2 mm cube (voxel) Time resolution 2 secs. Subject can be ‘resting’ or ‘working’ on task • One can study f. MRI data to discover http: //www. youtube. com/watch? v=2 kgn 7 j. Ft 1 v s voxel s – – – Brain’s operating principles at ‘rest’ [Heuvel et al 2010] time – Brain’s response to external stimuli [Mitchell et al 2008] – Differences between healthy and disease subjects [Atluri et al 2013]
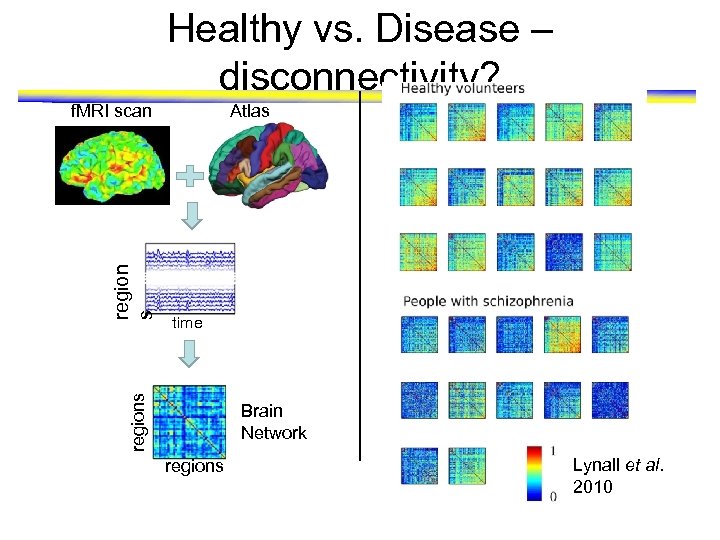
Healthy vs. Disease – disconnectivity? Atlas time regions region s f. MRI scan Brain Network regions Lynall et al. 2010
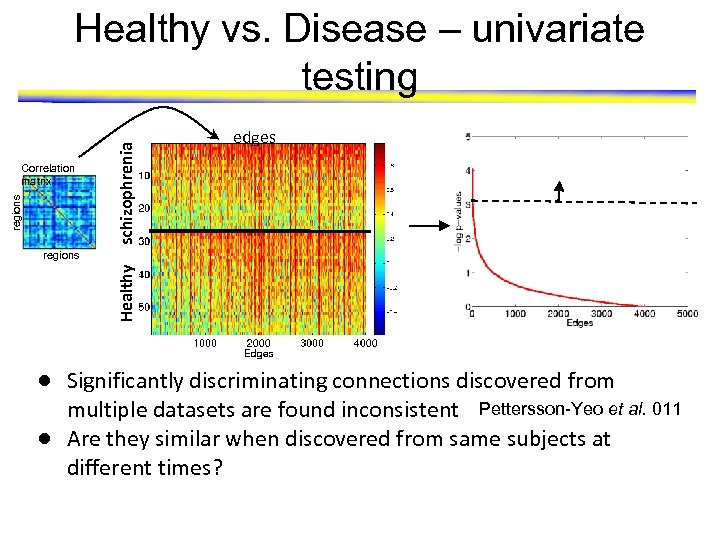
regions Correlation matrix schizophrenia Healthy vs. Disease – univariate testing edges Healthy regions ● Significantly discriminating connections discovered from multiple datasets are found inconsistent Pettersson-Yeo et al. 011 ● Are they similar when discovered from same subjects at different times?
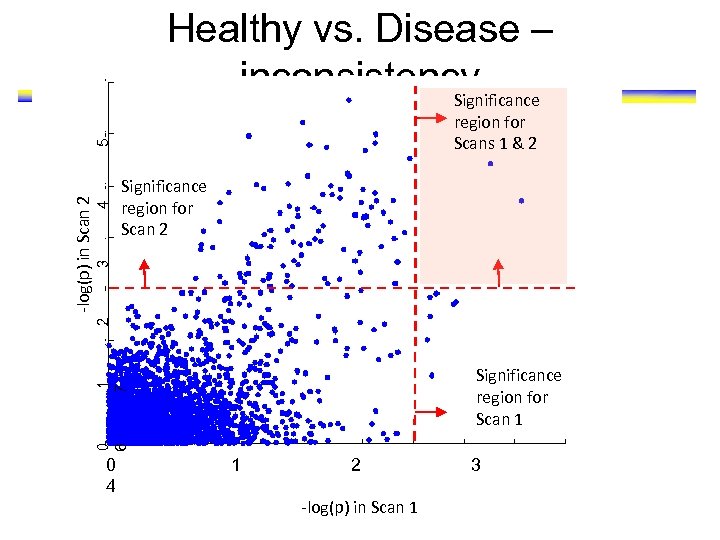
Healthy vs. Disease – inconsistency Significance 4 2 3 Significance region for Scan 2 1 7 Significance region for Scan 1 0 6 -log(p) in Scan 2 5 region for Scans 1 & 2 0 4 1 2 -log(p) in Scan 1 3
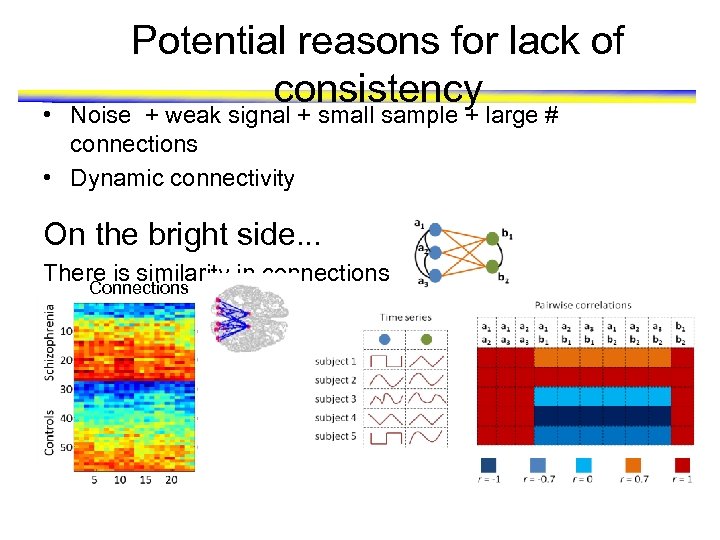
Potential reasons for lack of consistency • Noise + weak signal + small sample + large # connections • Dynamic connectivity On the bright side. . . There is similarity in connections Connections
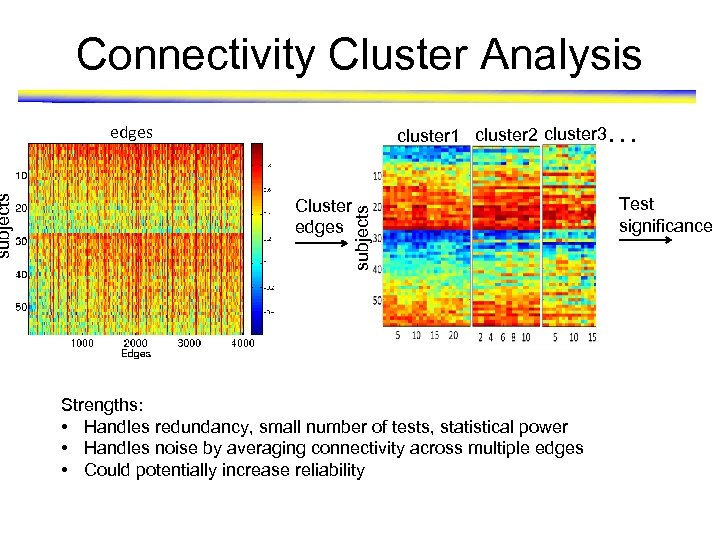
edges cluster 1 cluster 2 cluster 3. . . Cluster edges subjects Connectivity Cluster Analysis Strengths: • Handles redundancy, small number of tests, statistical power • Handles noise by averaging connectivity across multiple edges • Could potentially increase reliability Test significance
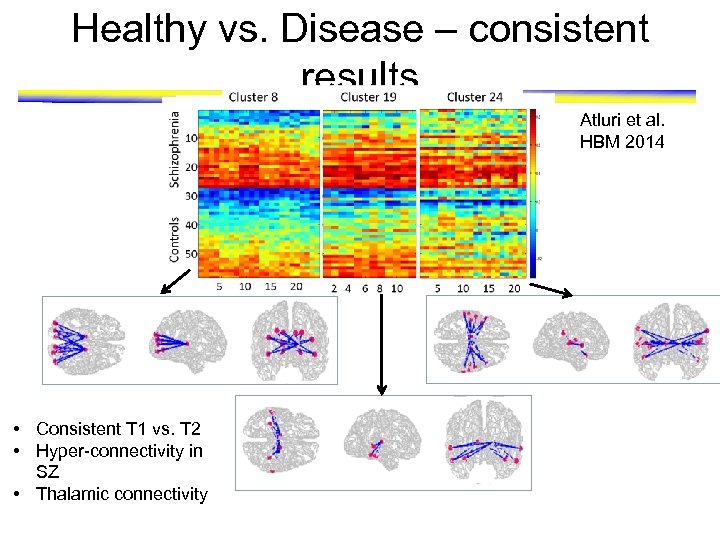
Healthy vs. Disease – consistent results Atluri et al. HBM 2014 • Consistent T 1 vs. T 2 • Hyper-connectivity in SZ • Thalamic connectivity
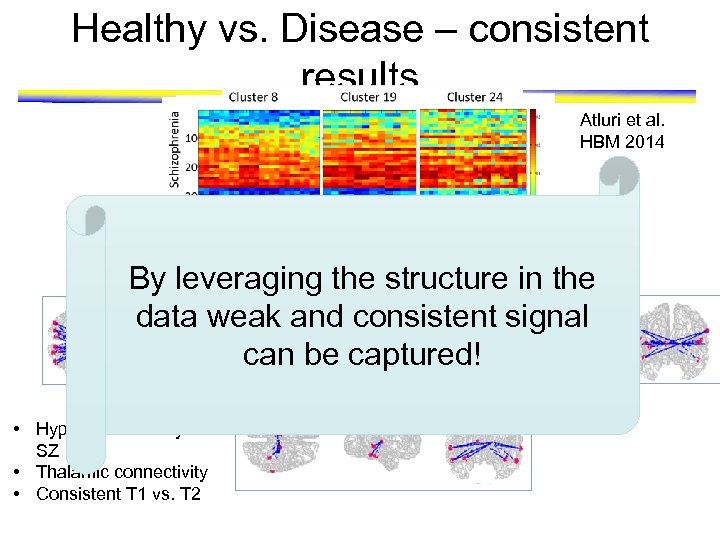
Healthy vs. Disease – consistent results Atluri et al. HBM 2014 By leveraging the structure in the data weak and consistent signal can be captured! • Hyper-connectivity in SZ • Thalamic connectivity • Consistent T 1 vs. T 2

Case Study 2 Home Health Care

Problem • In United States, 2010: – 4. 9 million people required help to complete ADLs – 9. 1 million people unable to complete IADLs 1 • Home Healthcare (HHC) – Spending in 1980 increased from $2. 4 billion to $17. 7 billion today – Report improved mobility in 46. 9% adults before discharge from HHC 2 • Mobility is one component of functional status – Mobility affects functional status and functional disability – Less than one-third of older adults recover pre-hospital function 3 – Increased risk of falls in home, rehospitalization, disability, social isolation, loss of independence – Besides physical issues, also psychosocial issues, comorbidity and death 1. Adams, Martinez, Vickerie, and Kirzinger, 2011; 2. Agency for Healthcare Research and Quality, 2012; 3. Chen, Wang, and Huang, 2008

Purpose of Study • To discover patients and support system characteristics associated with the improved outcomes of mobility • Find new factors associated with mobility besides the existing knowledge (current ambulation status during admission) • In each subgroup of patients defined by current ambulation status during admission (1 -5) – We started with group 2 and then compare the observations with other groups • To compare the predictors across each patient subgroup to find the consistent biomarkers in all subgroups and specific factors in each subgroup
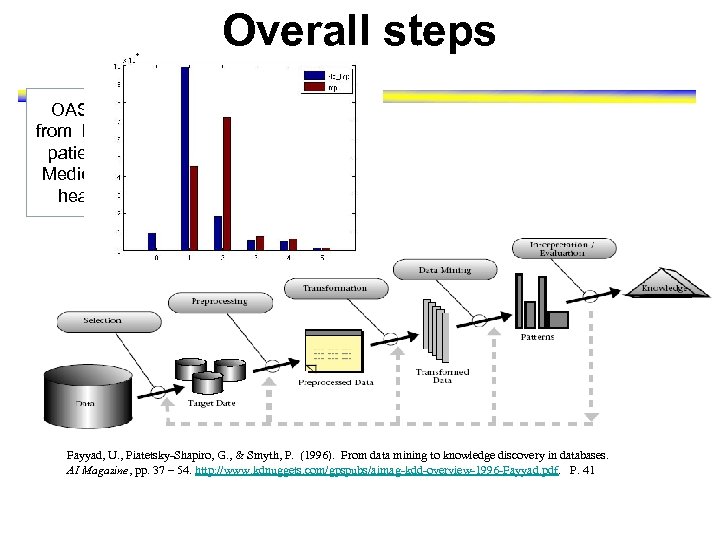
Overall steps OASISStandardizing data, dedata extracted from EHRs from 270, 634 identifying patient, patients served missing values, imputing by 581 Medicare-certified home binarizing data into 98 healthcare agencies variables Fayyad, U. , Piatetsky-Shapiro, G. , & Smyth, P. (1996). From data mining to knowledge discovery in databases. AI Magazine, pp. 37 – 54. http: //www. kdnuggets. com/gpspubs/aimag-kdd-overview-1996 -Fayyad. pdf. P. 41
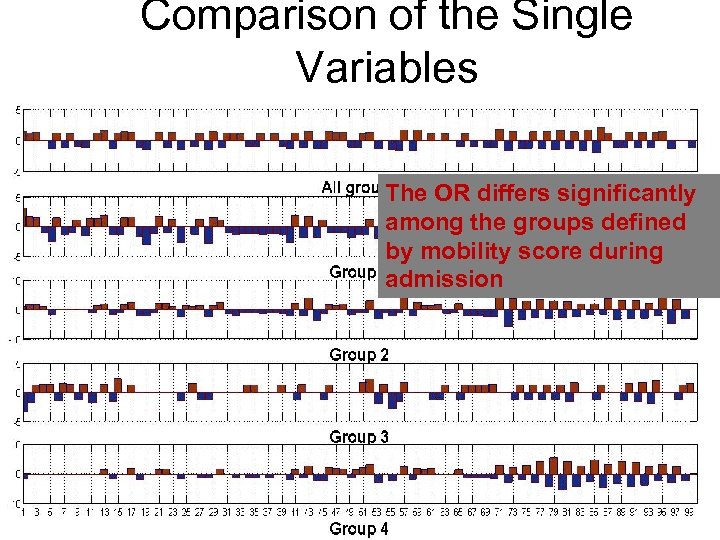
Comparison of the Single Variables The OR differs significantly among the groups defined by mobility score during admission

Data mining techniques • We found the risk variables that are significantly associated with mobility outcome vary among the groups • Group the single predictors based on whether they cover same or different patient group – Clustering • Based on similarity of sample space • Not discriminative • High frequency variables got merged – Pattern mining based approach • Discriminative • Coherence (similarity of sample space)
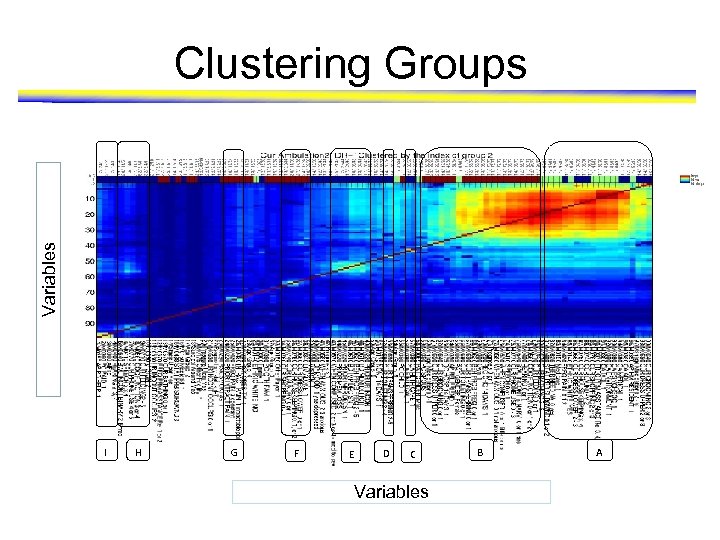
Variables Clustering Groups I H G F E D C Variables B A
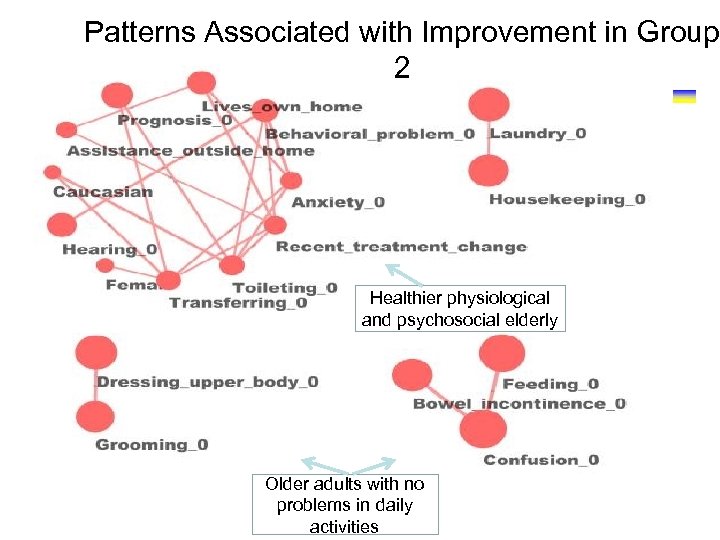
Patterns Associated with Improvement in Group 2 Healthier physiological and psychosocial elderly Older adults with no problems in daily activities
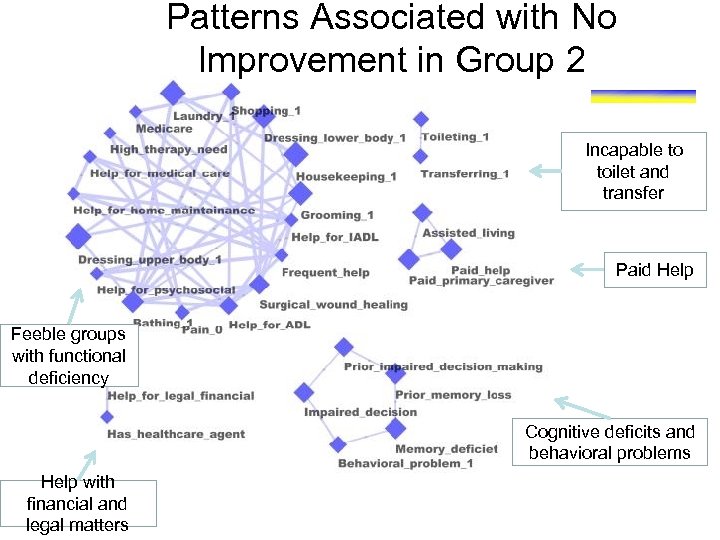
Patterns Associated with No Improvement in Group 2 Incapable to toilet and transfer Paid Help Feeble groups with functional deficiency Cognitive deficits and behavioral problems Help with financial and legal matters
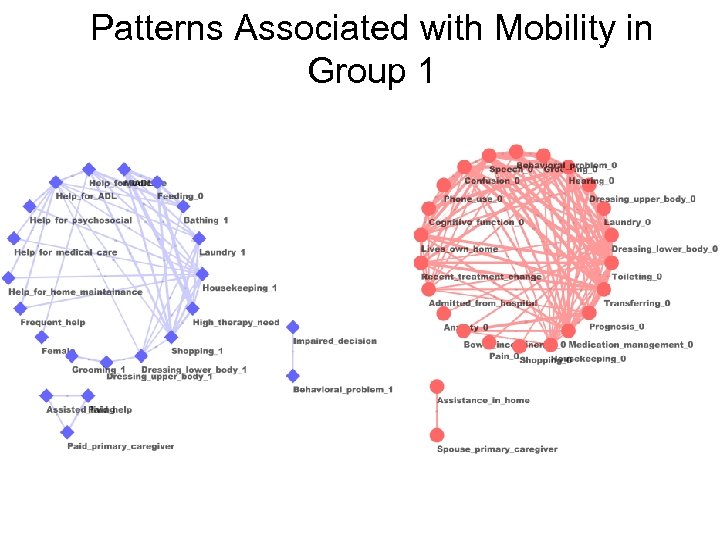
Patterns Associated with Mobility in Group 1
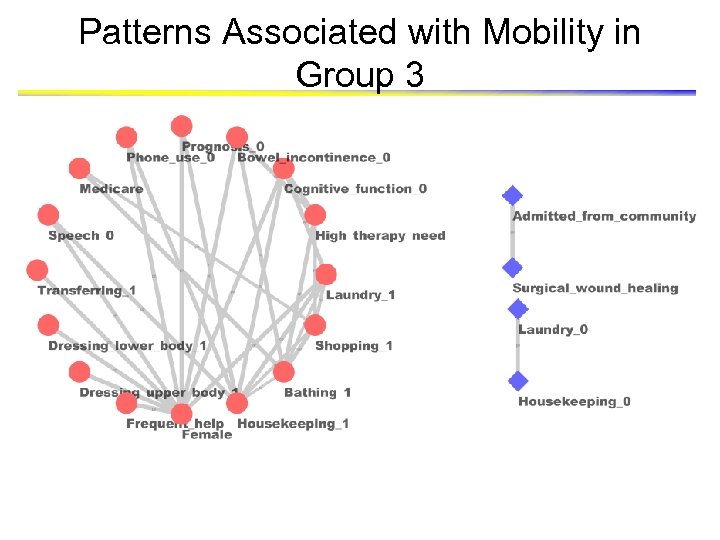
Patterns Associated with Mobility in Group 3
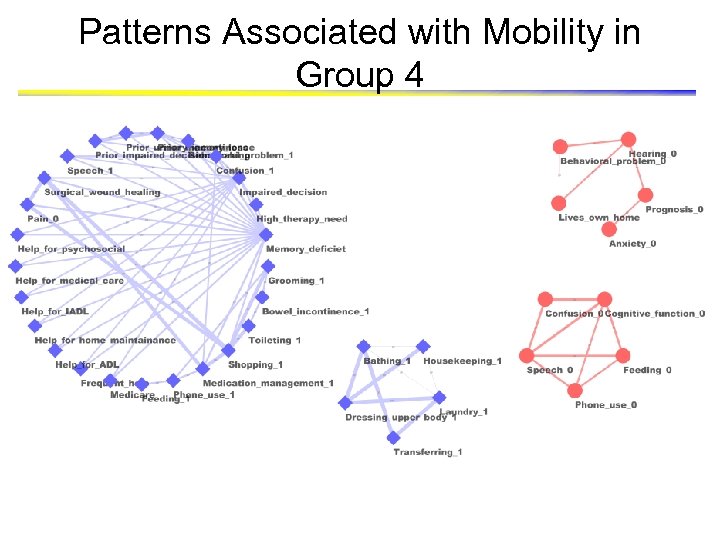
Patterns Associated with Mobility in Group 4

Discussion • High prevalence of mobility limitations in HHC patients (97%) • Mobility status at admission highest predictor of improvement – CMS outcome reporting controling for this, but doesn’t look at differences by mobility status • Variations of predictors within subgroups • Different clusters point to the need to tailor interventions for subgroups

Discussion (Cont. ) • Single variables may be less helpful than patterns of variables – higher categories • Large national sample – but not random – May be bias in results • Length of stay may vary and contribute to findings • Results are knowledge discovery, not hypotheses testing • Integrate diagnosis codes (icd-9) and nursing interventions in future to combine factors related to mobility

References • • Book Computational Approaches for Protein Function Prediction, Gaurav Pandey, Vipin Kumar and Michael Steinbach, to be published by John Wiley and Sons in the Book Series on Bioinformatics in Fall 2007 • • Conferences/Workshops Association Analysis-based Transformations for Protein Interaction Networks: A Function Prediction Case Study Gaurav Pandey, Michael , Steinbach, Rohit Gupta, Tushar Garg and Vipin Kumar, to appear, ACM SIGKDD 2007 • Incorporating Functional Inter-relationships into Algorithms for Protein Function Prediction, Gaurav Pandey and Vipin Kumar, to appear, ISMB satellite meeting on Automated Function Prediction 2007 • Comparative Study of Various Genomic Data Sets for Protein Function Prediction and Enhancements Using Association Analysis Rohit , Gupta, Tushar Garg, Gaurav Pandey, Michael Steinbach and Vipin Kumar, To be published in the proceedings of the Workshop on Data Mining for Biomedical Informatics, held in conjunction with SIAM International Conference on Data Mining, 2007 • Identification of Functional Modules in Protein Complexes via Hyperclique Pattern Discovery, Hui Xiong, X. He, Chris Ding, Ya Zhang, Vipin Kumar and Stephen R. Holbrook, pp 221 -232, Proc. of the Pacific Symposium on Biocomputing, 2005 • Feature Mining for Prediction of Degree of Liver Fibrosis, Benjamin Mayer, Huzefa Rangwala, Rohit Gupta, Jaideep Srivastava, George Karypis, Vipin Kumar and Piet de Groen, Proc. Annual Symposium of American Medical Informatics Association (AMIA), 2005 • • Technical Reports Association Analysis-based Transformations for Protein Interaction Networks: A Function Prediction Case Study Gaurav Pandey, Michael , Steinbach, Rohit Gupta, Tushar Garg, Vipin Kumar, Technical Report 07 -007, March 2007, Department of Computer Science, University of Minnesota • Computational Approaches for Protein Function Prediction: A Survey, Gaurav Pandey, Vipin Kumar, Michael Steinbach, Technical Report 06 -028, October 2006, Department of Computer Science, University of Minnesota
af8650e4e4dcb8768eeb6cf1ff749fd1.ppt