Minimizing Efficiency Loss in Mechanism and Protocol Design

Minimizing Efficiency Loss in Mechanism and Protocol Design Tim Roughgarden (Stanford) includes joint work with: Shuchi Chawla (Wisconsin), Ho-Lin Chen (Stanford), Aranyak Mehta (IBM Almaden), Mukund Sundararajan (Stanford), Gregory Valiant (UC Berkeley)

Reasons for Efficiency Loss Non-cooperative equilibria: n no control of underlying game, players' actions Auction design: n players have private "valuations" for goods n can use VCG mechanism to maximize efficiency n but suboptimality inevitable if goal includes: q q q poly-time + hard allocation (combinatorial auctions) different (e. g. maxmin) objective [Nisan/Ronen 99] revenue constraints 2

Quantifying Efficiency Loss Early applications: n price of anarchy [Kousoupias/Papadimitriou 99], etc. n approximation mechanisms q both poly-time combinatorial auctions and maxmin objectives This talk: mechanism/protocol design to minimize worst-case efficiency loss. n mechanism design s. t. revenue constraint n protocol design to minimize price of anarchy q full information but implementation constraints 3

Cost-Sharing Problems n general case: set U of players, cost function C defined on U (incurred by mechanism) q q n special case: fixed-tree-multicast rooted tree T with fixed edge costs c; C(S) = cost of subtree spanning S [Feigenbaum/Papadimitriou/Shenker 00] player i has valuation vi for winning Terminology: n surplus of S = v(S) - C(S) [where v(S) = Σi vi] 4

Cost-Sharing Mechanisms n cost-sharing mechanism: collect bids, pick winning set S, determines prices for winners Natural goals: n truthful + "individually rational" n economically efficient (maximizes surplus) n "budget-balance" (revenue covers cost incurred) q n VCG fails miserably here fact: 3 goals mutually incompatible [Green/Laffont, Roberts 70 s], [Feigenbaum/Krishnamurthy/Sami/Shenker 03] 5

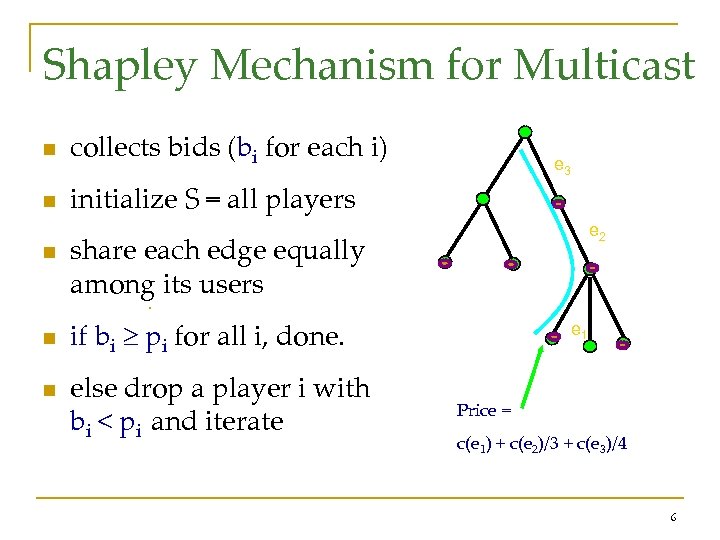Shapley Mechanism for Multicast n collects bids (bi for each i) n initialize S = all players n e 3 e 2 share each edge equally among its users § n n if bi pi for all i, done. else drop a player i with bi < pi and iterate e 1 Price = c(e 1) + c(e 2)/3 + c(e 3)/4 6

Moulin Mechanisms [Moulin 99] Given: cost fn C(S) on subsets S of U e 3 Cost-Sharing Method: for every set S, defines a cost share χ(i, S) for every i in S (“suggested prices”) Defn: χ is ß-budget-balanced (ß-BB) if prices charged within ß of C(S) e 2 e 1 Price = c(e 1) + c(e 2)/3 + c(e 3 )/4 Moulin mechanism: simulate ascending auction using χ to compute prices at each iteration. 7

Moulin Mechanisms: Good News Fact: [Moulin 99] if cost-sharing method χ is monotone (price for each player only increases), then the Moulin mechanism is truthful. q q utility = vi- pi if i wins, 0 otherwise reason: same as a classical ascending auction Also: n groupstrategyproof (form of collusion-resistance) n prices charged cover cost incurred (up to ß factor) 8

Moulin Mechanisms: Bad News Claim: Moulin mechanisms (e. g. , the Shapley mechanism) need not maximize surplus. e 1 = 1 + k players with valuations: 1, 1/2, 1/3, … , 1/k 9

Moulin Mechanisms: Bad News Claim: Moulin mechanisms (e. g. , the Shapley mechanism) need not maximize surplus. e 1 = 1 + n k players with valuations: 1, 1/2, 1/3, … , 1/k opt surplus (ln k) - 1, Shapley surplus = 0 10

Moulin Mechanisms: Bad News Claim: Moulin mechanisms (e. g. , the Shapley mechanism) need not maximize surplus. e 1 = 1 + n k players with valuations: 1, 1/2, 1/3, … , 1/k opt surplus (ln k) - 1, Shapley surplus = 0 Negative result [GL, R, FKSS]: no truthful mechanism gets non-trivial approximation of BB + surplus. 11

Measuring Surplus Loss Goal: minimize worst-case surplus loss. q surplus of S: v(S) - C(S) Defn: social cost of S: π(S) = C(S) + v(US) q q U = set of all players note: social cost = -surplus + v(U) e 1 = 1 + 1, 1/2, 1/3, … , 1/k Bad example: opt social cost 1, Shapley social cost ln k 12

Measuring Surplus Loss Goal: minimize worst-case surplus loss. q surplus of S: v(S) - C(S) Defn: social cost of S: π(S) = C(S) + v(US) q q U = set of all players note: social cost = -surplus + v(U) e 1 = 1 + 1, 1/2, 1/3, … , 1/k Bad example: opt social cost 1, Shapley social cost ln k Defn: a mechanism is α-approximate if it is an αapproximation algorithm w. r. t. the social cost objective (in the usual sense). 13

Goal + Main Result High-level goal: subject to reasonable BB, design mechanism with smallest approximation factor. n n note: requires both upper + lower bound results precisely quantifies inevitable surplus loss 14

Goal + Main Result High-level goal: subject to reasonable BB, design mechanism with smallest approximation factor. n n note: requires both upper + lower bound results precisely quantifies inevitable surplus loss Main result: complete soln for Moulin mechanisms. q [Roughgarden/Sundararajan STOC 06], [Chawla+R+S WINE 06], [R+S IPCO 07] 15

Goal + Main Result High-level goal: subject to reasonable BB, design mechanism with smallest approximation factor. n n note: requires both upper + lower bound results precisely quantifies inevitable surplus loss Main result: complete soln for Moulin mechanisms. q [Roughgarden/Sundararajan STOC 06], [Chawla+R+S WINE 06], [R+S IPCO 07] Ex: multicast: Shapley is optimal Moulin mechanism q q approximation factor of social cost = Hk extends to all submodular cost functions 16

More Examples: n uncapacitated facility location: the [Pal-Tardos 03] mechanism = optimal Moulin mechanism q n optimal approximation = Θ(log k) Steiner tree: the [Jain-Vazirani 01] mechanism = optimal Moulin mechanism q q optimal approximation factor of social cost = Θ(log 2 k) also extends to Steiner forest mechanism of [Konemann/Leonardi/Schaefer SODA 05] and rent-or buy mechanism of [Gupta/Srinivasan/Tardos 03] 17

Proof Techniques Part I: (problem-independent) n identify parameter of a monotone cost-sharing method that controls approximation factor of Moulin mechanism [upper and lower bounds] q reduces property of mechanism to property of method Part II: (problem-dependent) n prove upper bound on parameter for favorite mechanisms, lower bound for all mechanisms q has flavor of analysis of online algorithms 18

A Natural Lower Bound n n n consider a cost-sharing method χ for C + corresponding Moulin mechanism M e 1 = 1 + order the players of U = {1, 2, . . . , k} let xi = χ(i, {1, 2, . . . , i}) 1, 1/2, 1/3, … , 1/k set vi = xi - M outputs Ø, social cost Σi xi ; OPT is ≤ C(U) Σi χ(i, {1, 2, . . . , i})/C(U) lower bounds approximation factor 19

A Natural Lower Bound n n n consider a cost-sharing method χ for C + corresponding Moulin mechanism M e 1 = 1 + order the players of U = {1, 2, . . . , k} let xi = χ(i, {1, 2, . . . , i}) 1, 1/2, 1/3, … , 1/k set vi = xi - M outputs Ø, social cost Σi xi ; OPT is ≤ C(U) Σi χ(i, {1, 2, . . . , i})/C(U) lower bounds approximation factor Defn: the summability α of χ for C is the largest lower bound arising in this way. 20

A Key Theorem Summary: a Moulin mechanism based on an αsummable cost-sharing method is no better than α-approximate. 21

A Key Theorem Summary: a Moulin mechanism based on an αsummable cost-sharing method is no better than α-approximate. Theorem [Roughgarden/Sundararajan STOC 06]: a Moulin mechanism based on an α-summable, ßBB cost-sharing method is (α+ß)-approximate. Point: for every O(1)-BB method χ, the parameter α completely characterizes the approximation factor of the corresponding mechanism. 22

Beyond Moulin Mechanisms Question: why obsessed with Moulin mechanisms? q q q only general technique to achieve truthful + BB strong lower bounds for approximation for some problems [Immorlica/Mahdian/Mirrokni SODA 05] non-trivial to design (e. g. , for UFL) 23

Beyond Moulin Mechanisms Question: why obsessed with Moulin mechanisms? q q q only general technique to achieve truthful + BB strong lower bounds for approximation for some problems [Immorlica/Mahdian/Mirrokni SODA 05] non-trivial to design (e. g. , for UFL) Acyclic Mechanisms [Mehta/Roughgarden/Sundararajan EC 07]: generalizes Moulin mechanisms. q q q idea: order offers within iteration of ascending auction most "off-the-shelf" primal-dual algorithms work as is exponentially better BB + efficiency for e. g. Set Cover 24

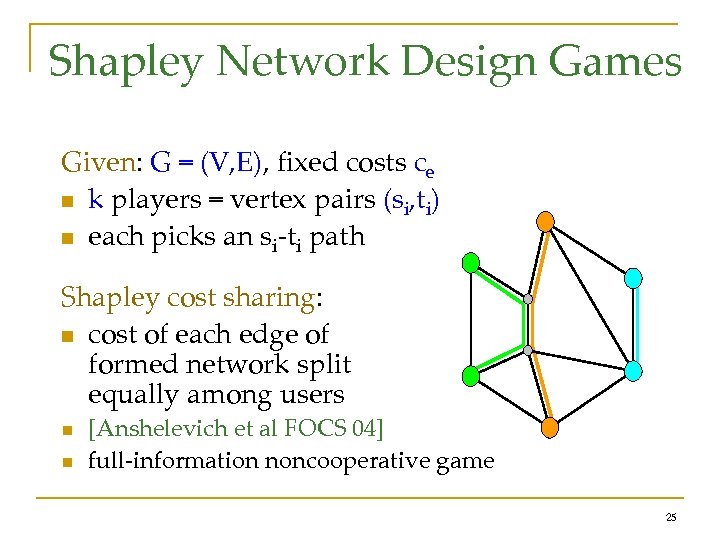Shapley Network Design Games Given: G = (V, E), fixed costs ce n k players = vertex pairs (si, ti) n each picks an si-ti path Shapley cost sharing: n cost of each edge of formed network split equally among users n n [Anshelevich et al FOCS 04] full-information noncooperative game 25

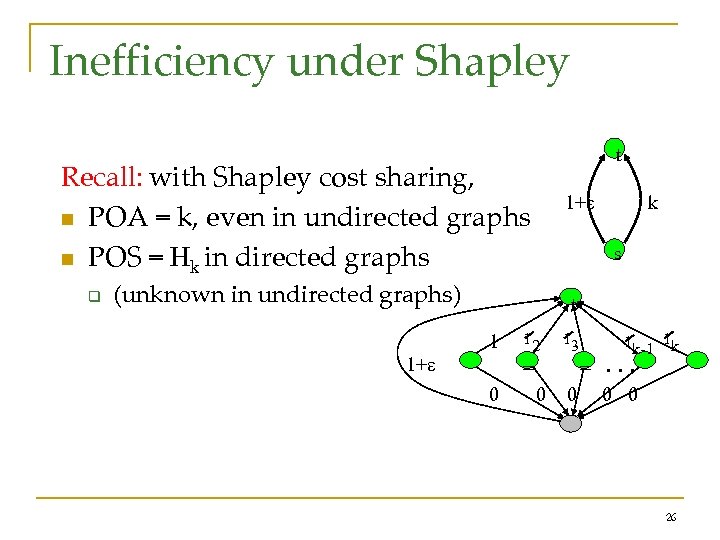Inefficiency under Shapley t Recall: with Shapley cost sharing, n POA = k, even in undirected graphs n POS = Hk in directed graphs q 1+ k s (unknown in undirected graphs) t 1 1+ 12 13 = 0 0 1 k-1 1 k . . . 0 0 26

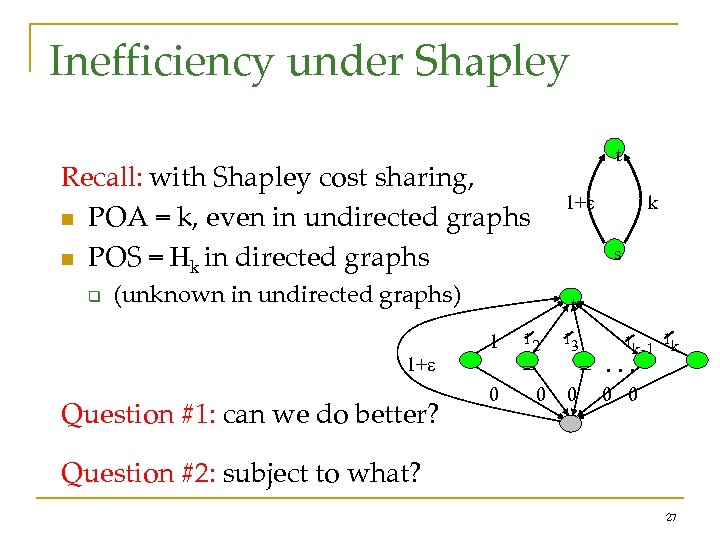Inefficiency under Shapley t Recall: with Shapley cost sharing, n POA = k, even in undirected graphs n POS = Hk in directed graphs q 1+ s (unknown in undirected graphs) t 1 1+ Question #1: can we do better? k 12 13 = 0 0 1 k-1 1 k . . . 0 0 Question #2: subject to what? 27

In Defense of Shapley Essential properties: (non-negotiable) n "budget-balanced" (total cost shares = cost) n "separable" (cost shares defined edge-by-edge) n pure-strategy Nash equilibria exist Bonus good properties: (negotiable) n "uniform" (same definition for all networks) n "fair" (characterizes Shapley) 28

Key Question The Problem: design edge cost-sharing methods to minimize worst-case POA and/or POS. q q directed vs. undirected uniform vs. non-uniform single-sink vs. terminal pairs [Chen/Roughgarden/Valiant 07] Related work: coordination mechanisms [Christodoulou/Koutsoupias/Nanavati ICALP 04], [Immorlica/Li/Mirrokni/Schulz 05], [Azar et al 07] n resource allocation [Johari/Tsitsiklis 07] 29

Directed Graphs Negative result: worst-case POA = k for every cost-sharing method, even non-uniform. 30

Directed Graphs Negative result: worst-case POA = k for every cost-sharing method, even non-uniform. Theorem: Shapley is the optimal uniform costsharing method! For every method, either: (1) there is a network game s. t. POS Hk OR (2) there is a network game with no Nash eq. 31

Directed Graphs Negative result: worst-case POA = k for every cost-sharing method, even non-uniform. Theorem: Shapley is the optimal uniform costsharing method! For every method, either: (1) there is a network game s. t. POS Hk OR (2) there is a network game with no Nash eq. q q Shapley can be justified on efficiency grounds, not just usual fairness/simplicity reasons open: what's up with non-uniform methods? 32

Undirected Graphs: Uniform Theorem: in undirected graphs, can reduce the worst-case POA to polylogarithmic! n simple uniform priority-based scheme n POA = O(log k) in with single sink, O(log 2 k) for pairs (follows from [IW 91], [AA 96]) 33

Undirected Graphs: Uniform Theorem: in undirected graphs, can reduce the worst-case POA to polylogarithmic! n simple uniform priority-based scheme n POA = O(log k) in with single sink, O(log 2 k) for pairs (follows from [IW 91], [AA 96]) Theorem: For every unform cost-sharing method, worst-case POA = Ω(log k). [even single-sink] q follows from complete characterization of uniform cost-sharing methods that always admit PNE 34

Undirected: Non-Uniform Theorem: Can reduce POA to 2 in single-sink networks via non-uniform method. n idea: use Prim MST to define priority scheme n easy: matching lower bound Theorem: For every non-uniform method, worstcase POA is general networks is Ω(log k). n extremal graph construction n lower bounds for "oblivious network design" 35

Open Questions Cost-Sharing Mechanism Design: n lower bounds for non-Moulin mechanisms n more applications of acyclic mechanisms n profit-maximization Optimal Protocol Design: n non-uniform methods in directed graphs n lower bounds for scheduling mechanisms n new applications (selfish routing, fair queuing) 36