Минимизация издержек Минимизация издержек Фирма стремится

Минимизация издержек

Минимизация издержек • Фирма стремится производить любой объем продукции при минимально возможных для этой технологии издержках. • Введем функцию C(Q), которая отражает наименьшие издержки производстве Q единиц продукции. • Она носит название функция общих издержек фирмы

Минимизация издержек При ценах на факторы (ресурсы, ингредиенты): w = (w 1, w 2, …, wn) функция общих издержек может быть записана: С(w 1, …, wn , Q). То есть для n факторов:

Функция затрат на производство • То есть для формирования функции затрат необходимо выяснить функции xi (Q) – функции спроса фирмы на фактор i • Для двухфакторной (труд и капитал) производственной функции: L (Q ), K(Q).

Минимизация издержек • Предположим, что используются только два фактора. • Производственная функция имеет вид: Q = f(x 1 , x 2 ) • При ценах на факторы w 1 и w 2, издержки любого набора факторов (x 1, x 2) можно представить следующим образом: C(Q) = w 1 x 1(Q) + w 2 x 2(Q)

Минимизация издержек • Для цен w 1, w 2 и конкретного объема выпуска Q, проблема минимизации издержек означает: если

Минимизация издержек/ два фактора: L и K – труд и капитал • Для цен w, r и объема выпуска Q, проблема минимизации издержек означает:

Минимизация издержек • Уровни затрат факторов x 1*(w 1, w 2, Q) и x 2*(w 1, w 2, Q) в минимизирующем издержки наборе факторов являются спросом фирмы на эти факторы 1 и 2. • Наименьшие издержки для производства объема Q можно выразить как:

Спрос на факторы, обусловленный спросом на продукт • При неизменных ценах на факторы w 1, w 2 и желаемом объеме выпуска Q определим такой набор факторов, при использовании которого издержки на производство минимальны. • Выразим функцию общих издержек, т. е. издержек С(Q) при w 1, w 2 = const

Изокоста • Линия, показывающая все возможные наборы факторов, стоимость которых одинакова, называется “изокостой”. изокостой • Например, при ценах на факторы w 1=3 и w 2=4, изокоста $100 имеет вид: =4

Изокоста • В общем виде при заданных ценах w 1 и w 2, выражение для изокосты имеет вид • Наклон изокосты равен коэффициенту ( - w 1/w 2 ).

Изокоста • Для двухфакторной модели (L и K) при заданных ценах w и r, выражение для изокосты имеет вид • Наклон изокосты равен коэффициенту ( - w/r )

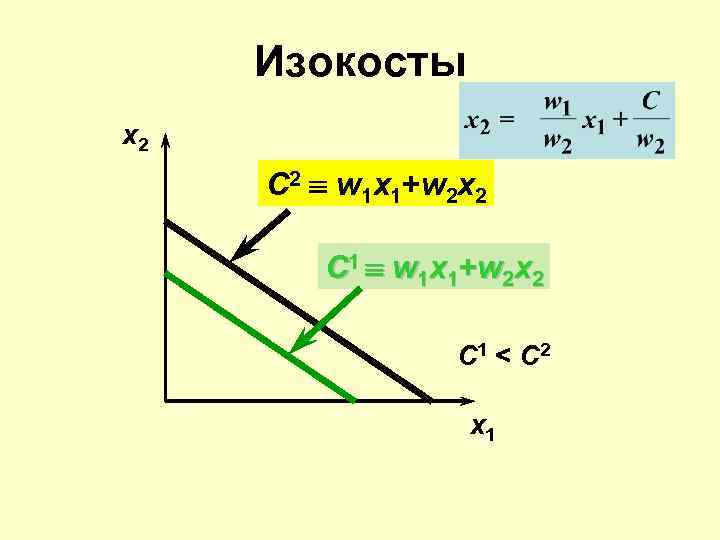Изокосты x 2 С 2 º w 1 x 1+w 2 x 2 С 1 º w 1 x 1+ w 2 x 2 С 1 < С 2 x 1

Изокосты x 2 С 2 º w 1 x 1+w 2 x 2 C 1 º w 1 x 1+ w 2 x 2 С 1 < С 2 x 1 Наклон = - w 1/w 2.

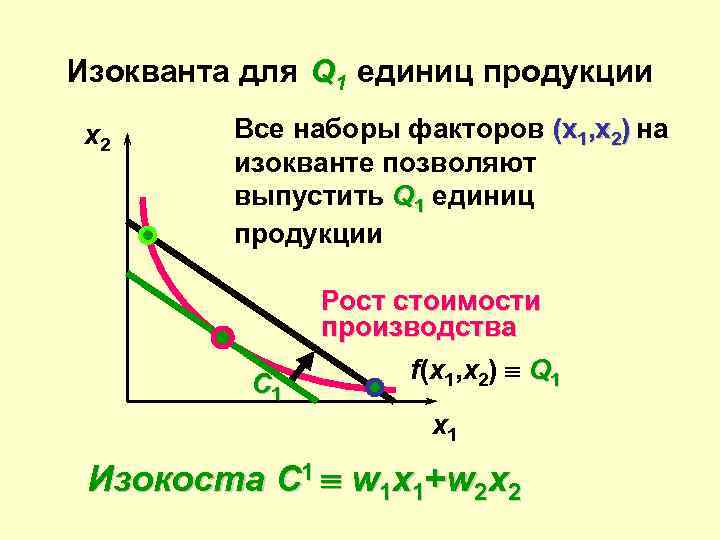Изокванта для Q 1 единиц продукции x 2 Все наборы факторов (x 1, x 2) на изокванте позволяют выпустить Q 1 единиц продукции С 1 Рост стоимости производства f(x 1, x 2) º Q 1 x 1 Изокоста C 1 º w 1 x 1+w 2 x 2

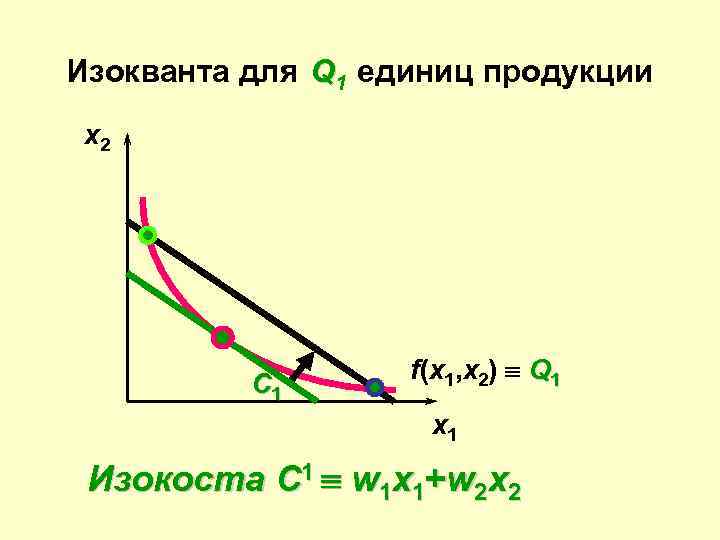Изокванта для Q 1 единиц продукции x 2 С 1 f(x 1, x 2) º Q 1 x 1 Изокоста C 1 º w 1 x 1+w 2 x 2

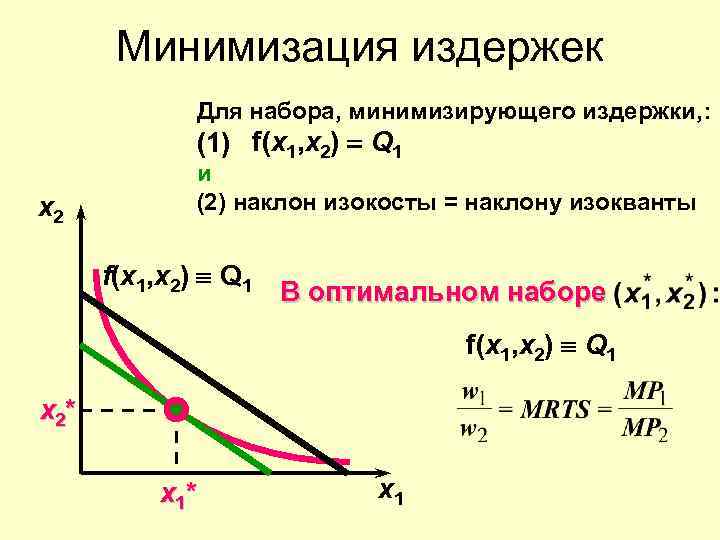Минимизация издержек Для набора, минимизирующего издержки, : (1) f(x 1, x 2) = Q 1 x 2 и (2) наклон изокосты = наклону изокванты f(x 1, x 2) º Q 1 В оптимальном наборе f(x 1, x 2) º Q 1 x 2* x 1

Минимизация издержек Условие равновесия производителя при использовании двух факторов и производстве Q единиц продукции: ИЛИ:

Минимизация издержек для функции Кобба-Дугласа • Функция производства Кобба-Дугласа • Цены на факторы w 1 и w 2. • Как определяется спрос на факторы со стороны фирмы?

Минимизация издержек для функции Кобба-Дугласа Для набора (x 1*, x 2*), при котором минимизируются издержки данного объема выпуска: (1) (2)

Минимизация издержек для функции Кобба-Дугласа (1) (2) Подставим в (1) и получим:

Минимизация издержек для функции Кобба-Дугласа Таким образом: Спрос на фактор 1

Минимизация издержек для функции Кобба-Дугласа Т. к. и Спрос на фактор 2

Минимизация издержек для функции Кобба-Дугласа Таким образом, наиболее дешевый набор факторов, с помощью которого можно произвести Q единиц продукции, определяется как функция от Q:

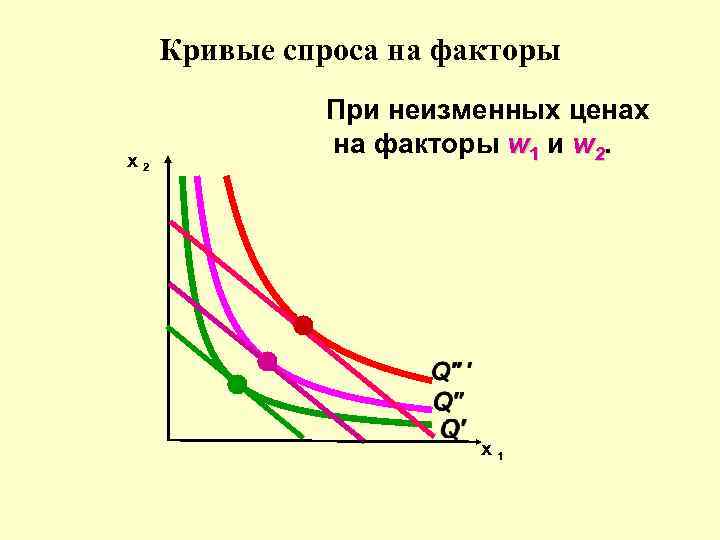Кривые спроса на факторы x 2 При неизменных ценах на факторы w 1 и w 2. x 1

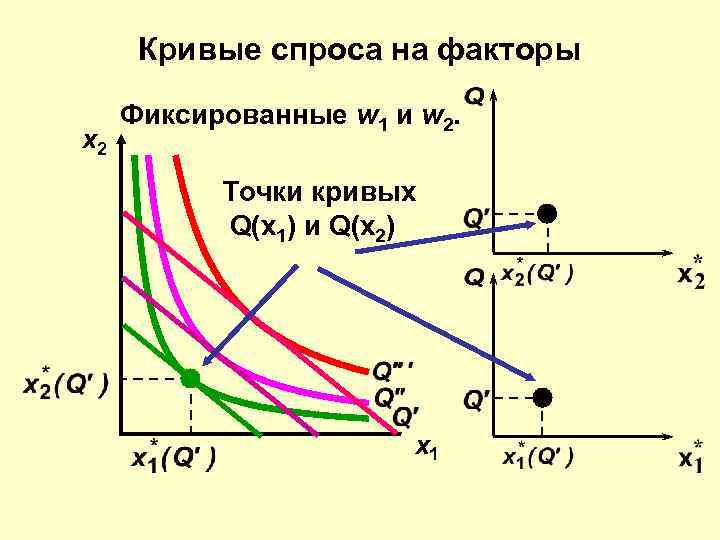Кривые спроса на факторы x 2 Фиксированные w 1 и w 2. Точки кривых Q(x 1) и Q(x 2) x 1

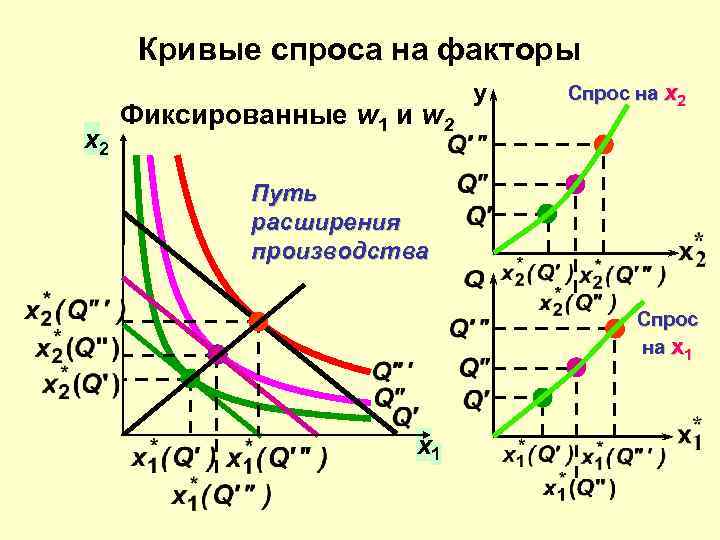Кривые спроса на факторы x 2 Фиксированные w 1 и w 2 y Спрос на x 2 Путь расширения производства Спрос на x 1

Минимизация издержек для функции Кобба-Дугласа Для производственной функции Самый дешевый набор (рис. 24):

Минимизация издержек для функции Кобба-Дугласа Поэтому функция общих издержек фирмы имеет вид:

Минимизация издержек для функции Кобба-Дугласа Преобразуем:

Минимизация издержек для функции Кобба-Дугласа т. е. функция издержек имеет вид прямой линии, выходящей из начала координат

Минимизация издержек для совершенно дополняющих факторов • Производственная функция имеет вид: • Цены заданы w 1 и w 2. • Определим спрос на факторы 1 и 2. • Выведем функцию общих издержек фирмы для этого случая.

Минимизация издержек для совершенно дополняющих факторов x 2 4 x 1 = x 2 min{4 x 1, x 2} º Q 1 4 1 x 1

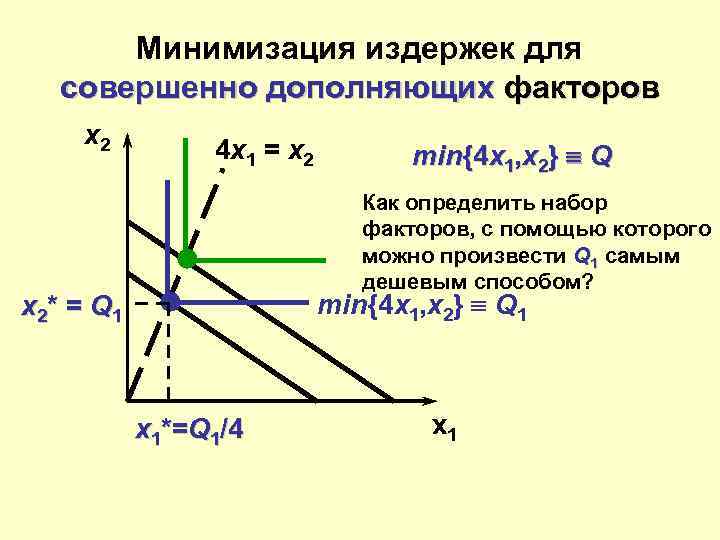Минимизация издержек для совершенно дополняющих факторов x 2 4 x 1 = x 2 min{4 x 1, x 2} º Q Как определить набор факторов, с помощью которого можно произвести Q 1 самым дешевым способом? min{4 x 1, x 2} º Q 1 x 2* = Q 1 x 1*=Q 1/4 x 1

Минимизация издержек для совершенно дополняющих факторов Производственная функция имеет вид: Спрос на факторы имеет вид: и Функция общих издержек фирмы имеет вид (общий вид): т. е. функция издержек имеет вид прямой линии, выходящей из начала координат

Средние общие издержки на производство • Для выпуска Q единиц продукции средние издержки выпуска (издержки на единицу продукции) вычисляются следующим образом: • Или • Например. AC = 120 000/100 = 1200 руб. /ед. продукции

Отдача от масштаба с точки зрения общих издержек • Отдача от масштаба, зависящая от масштаба технологии производства, определяет, как изменяются средние издержки (себестоимость продукции) в зависимости от изменения выпуска: AC(Q)

Отдача от масштаба с точки зрения средних общих издержек (AC) AC • Если фирма вследствие применения определенной технологии имеет постоянную отдачу от масштаба, то удвоение выпуска от масштаба Q’ до 2 Q’ единиц требует удвоения объема применения всех ресурсов • Общие издержки на производство продукции удваиваются • Средние издержки на единицу продукции остаются неизменными:

Снижающаяся отдача от масштаба и средние общие издержки (AC) AC • Если фирма вследствие применения определенной технологии имеет падающую отдачу от масштаба , то удвоение выпуска от Q’ до 2 Q’ требует увеличения применения факторов в более, чем два более раза • Общие издержки (TC)вырастут более, чем TC более в два раза • Средние издержки растут

Растущая отдача от масштаба и AТC § Если фирма вследствие применения определенной технологии имеет растущую отдачу от масштаба, то масштаба удвоение выпуска продукции от Q’ до 2 Q’ единиц, требует увеличения применяемых ресурсов менее, менее чем в два раза • Общие затраты (TC) на выпуск продукции растут в TC менее, чем в два раза. • Средние издержки (AC) снижаются AC

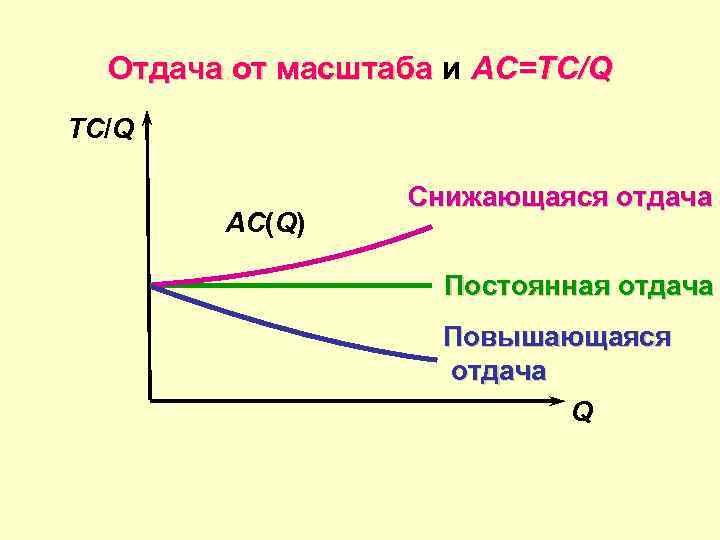Отдача от масштаба и AC=TC/Q AC(Q) Снижающаяся отдача Постоянная отдача Повышающаяся отдача Q

Пример Около 73% общего объема торговли стран ЕС легковыми автомобилями, грузовиками, бытовой электроникой мотивируется разницей в издержках, обусловленной различиями в масштабах производства В развитых странах в среднем удвоение выпуска компанией обеспечивает снижение удельных затрат: затрат Ø для отраслей обрабатывающей промышленности – на 10%, Ø в производстве бытовых электроприборов – на 15%, Ø в электронике – на 25 - 30%, Ø в производстве интегральных схем на – 28%.

Отдача от масштаба и TC • Как применить эти зависимости к форме функции общих издержек (TC)? TC

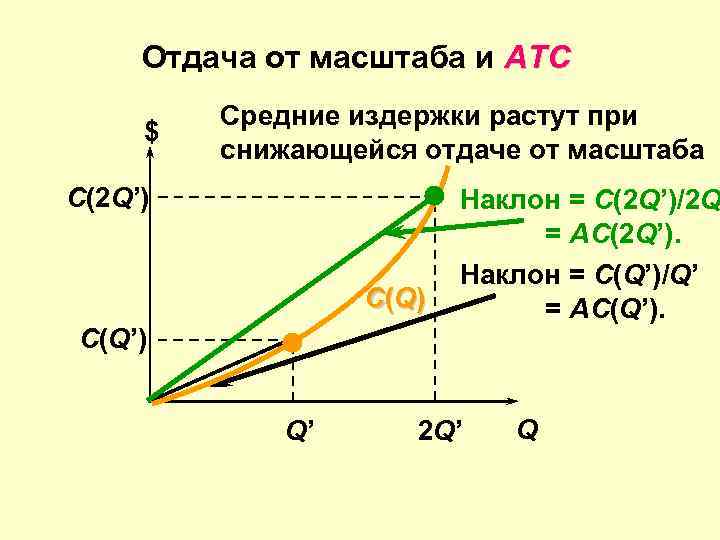Отдача от масштаба и ATC $ Средние издержки растут при снижающейся отдаче от масштаба C(2 Q’) C (Q ) C(Q’) Q’ Наклон = С(2 Q’)/2 Q = AC(2 Q’). Наклон = С(Q’)/Q’ = AC(Q’). 2 Q’ Q

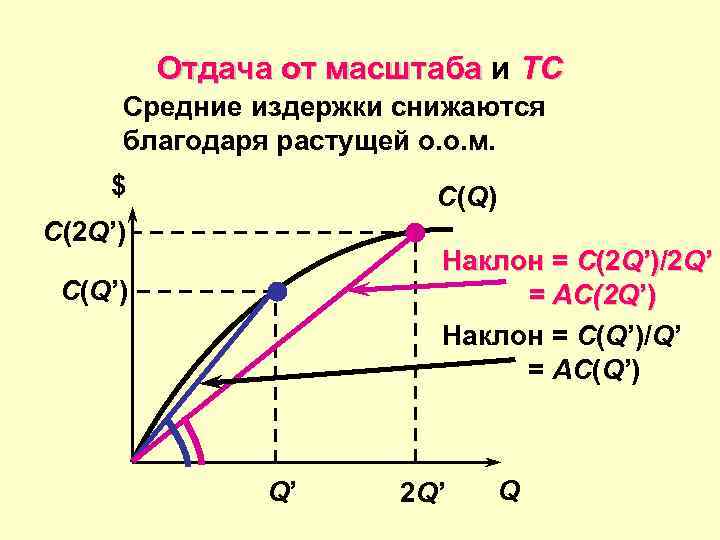Отдача от масштаба и TC Средние издержки снижаются благодаря растущей о. о. м. $ C(Q) C(2 Q’) Наклон = C(2 Q’)/2 Q’ = AC(2 Q’) Наклон = C(Q’)/Q’ = AC(Q’) Q’ 2 Q’ Q

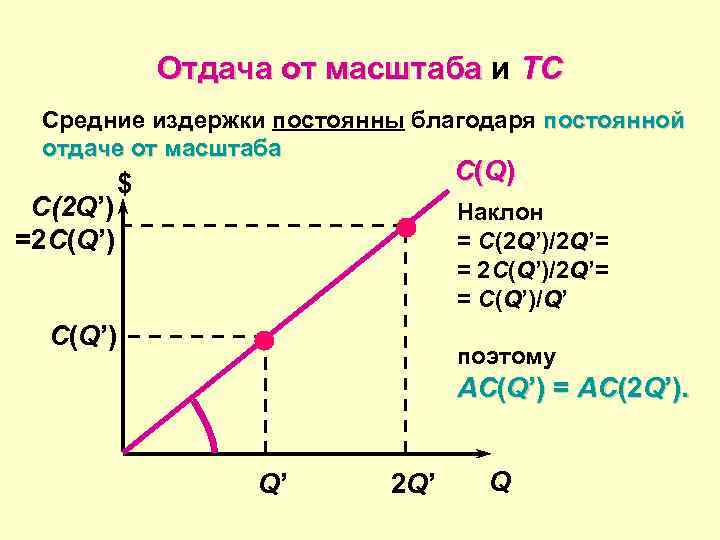Отдача от масштаба и TC Средние издержки постоянны благодаря постоянной отдаче от масштаба C(2 Q’) =2 C(Q’) C (Q ) $ Наклон = C(2 Q’)/2 Q’= = 2 C(Q’)/2 Q’= = C(Q’)/Q’ C(Q’) поэтому AC(Q’) = AC(2 Q’). Q’ 2 Q’ Q

Кратко- и долгосрочные общие издержки • В долгосрочном периоде фирма может изменить все уровни используемых издержек • Допустим, что фирма не может изменить издержки вида 2 и их объем составляет x 2’ единиц. • Сравним краткосрочные и долгосрочные общие издержки производства Q единиц продукции

Кратко- и долгосрочные общие издержки • Минимизация на долгосрочном периоде имеет вид: При выпуске • Минимизация на краткосрочном периоде (фактор 2 зафиксирован на уровне х2’) имеет вид: при

Кратко- и долгосрочные общие издержки • Краткосрочная минимизация издержек может быть получена из долгосрочной при дополнительном ограничении на один из факторов x 2 = x 2’. • Если на долгосрочном периоде x 2 = x 2’, то дополнительное ограничение x 2 = x 2’ не является значимым ограничением и поэтому издержки долго- и краткосрочного периодов производства Q единиц продукции одинаковы

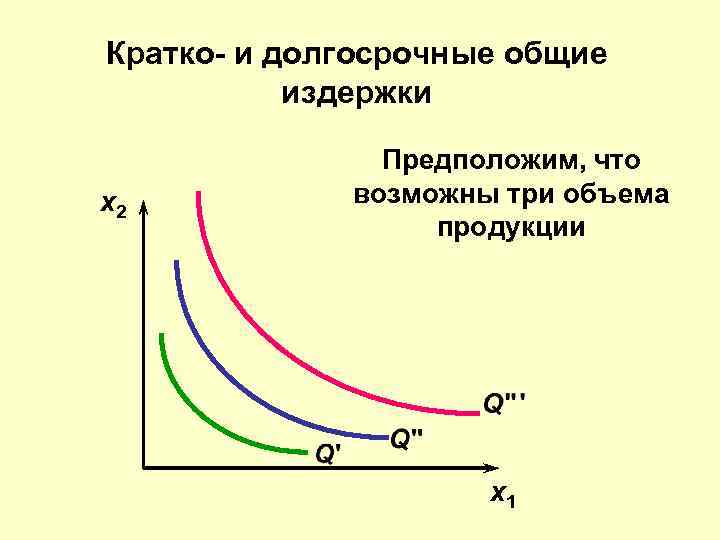Кратко- и долгосрочные общие издержки x 2 Предположим, что возможны три объема продукции x 1

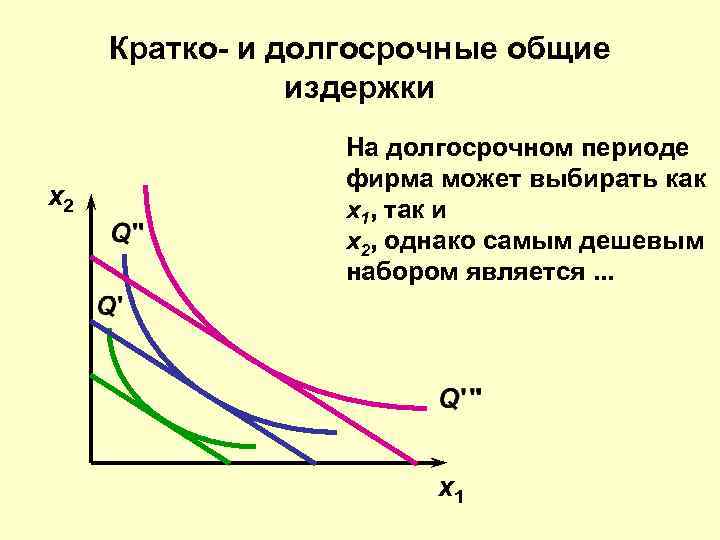Кратко- и долгосрочные общие издержки x 2 На долгосрочном периоде фирма может выбирать как x 1, так и x 2, однако самым дешевым набором является. . . x 1

Кратко- и долгосрочные общие издержки x 2 Долгосрочный путь расширения производства (предприятия) x 1

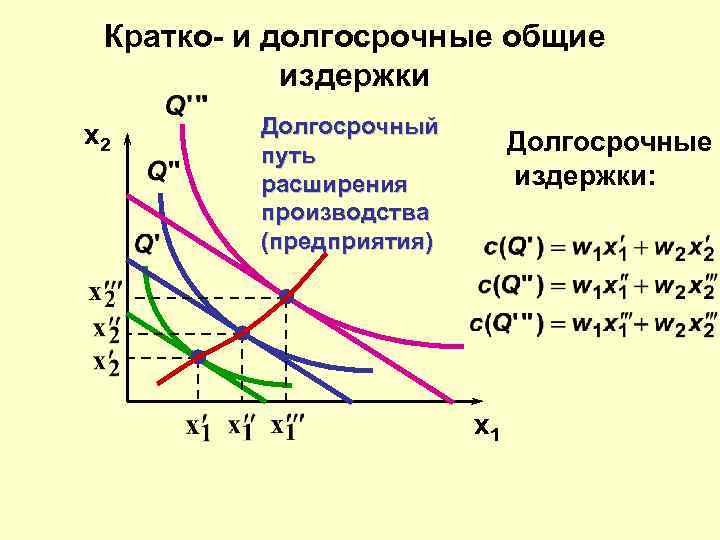Кратко- и долгосрочные общие издержки x 2 Долгосрочный путь расширения производства (предприятия) Долгосрочные издержки: x 1

Кратко- и долгосрочные общие издержки • Предположим, что фирма ограничена в объеме фактора на краткосрочном периоде, так что x 1 = x 1”.

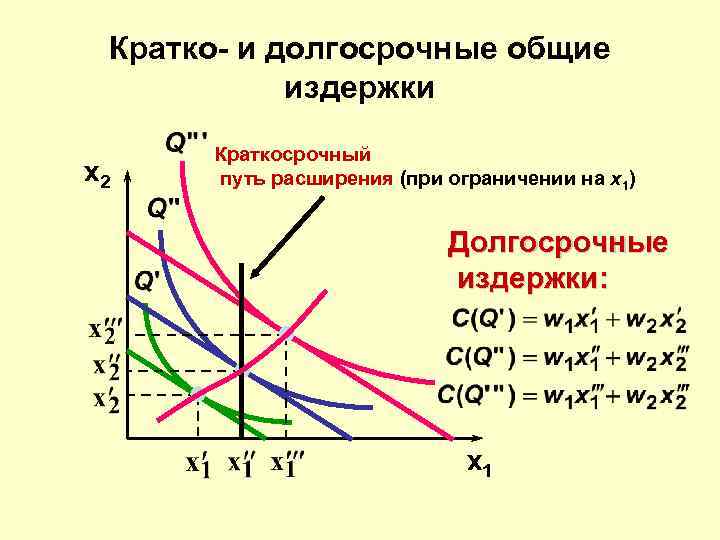Кратко- и долгосрочные общие издержки x 2 Краткосрочный путь расширения (при ограничении на x 1) Долгосрочные издержки: x 1

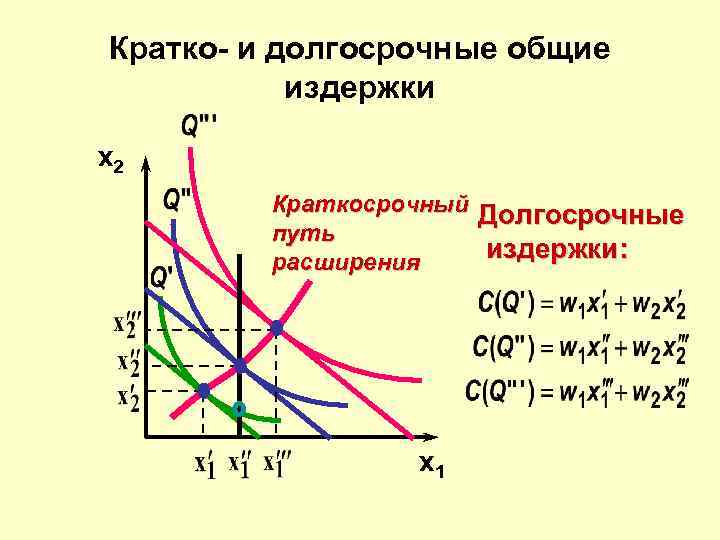Кратко- и долгосрочные общие издержки x 2 Краткосрочный Долгосрочные путь издержки: расширения x 1

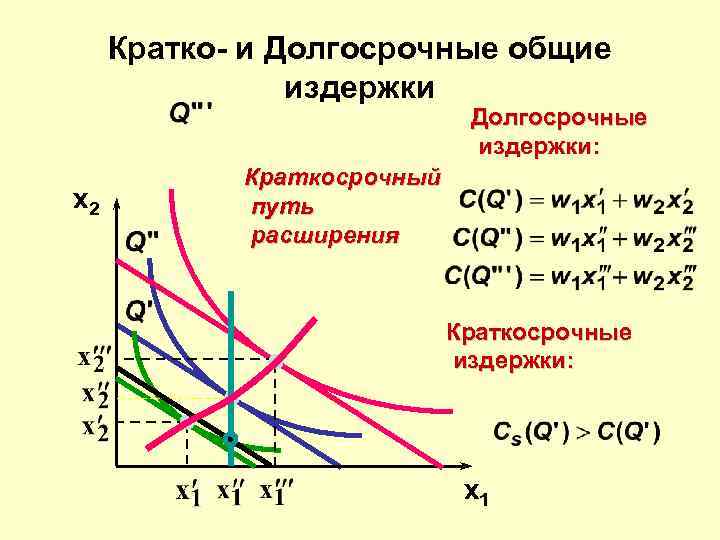Кратко- и Долгосрочные общие издержки Долгосрочные издержки: x 2 Краткосрочный путь расширения Краткосрочные издержки: x 1

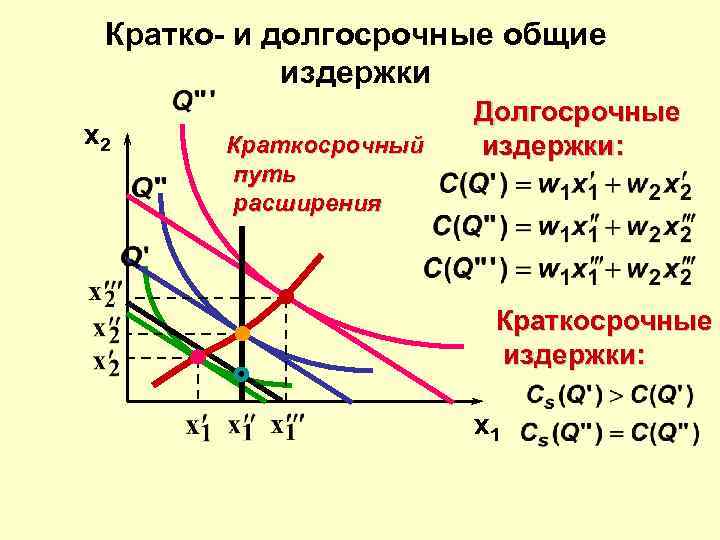Кратко- и долгосрочные общие издержки x 2 Краткосрочный путь расширения Долгосрочные издержки: Краткосрочные издержки: x 1

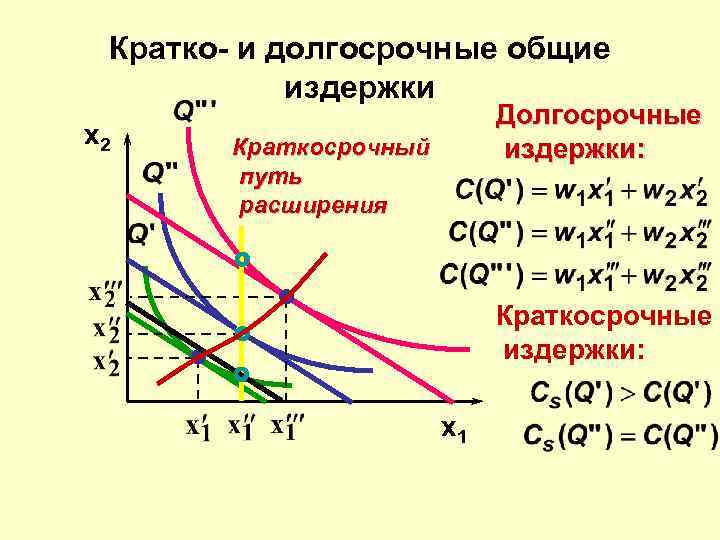Кратко- и долгосрочные общие издержки x 2 Долгосрочные издержки: Краткосрочный путь расширения Краткосрочные издержки: x 1

Кратко- и долгосрочные общие издержки • Краткосрочные общие издержки выше долгосрочных, кроме одного объема выпуска, где краткосрочный выпуск представляет собой также и долгосрочный выбор объема производства. • Таким образом кривая долгосрочных издержек всегда имеет одну общую с каждой из конкретных кривых краткосрочных издержек точку

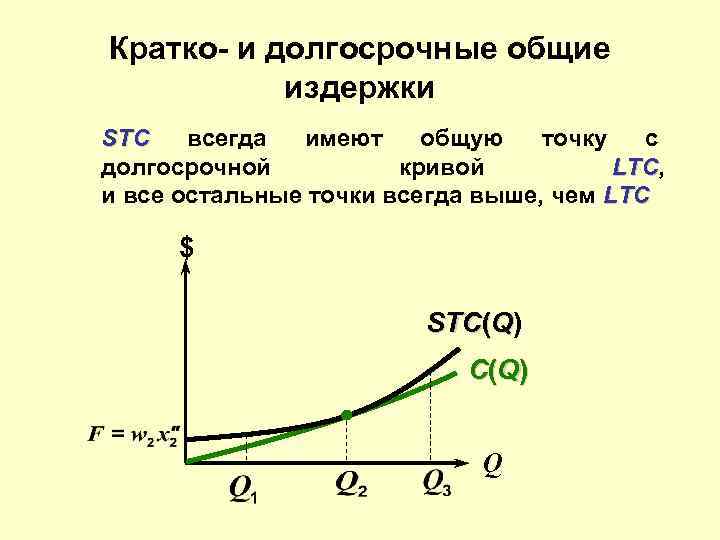Кратко- и долгосрочные общие издержки STC всегда имеют общую точку с долгосрочной кривой LTC, LTC и все остальные точки всегда выше, чем LTC $ STC(Q) С (Q ) Q