МІНІ Математична КЛАС 11 статистика ПІДРУЧНИК виконала студентка

МІНІ Математична КЛАС 11 статистика ПІДРУЧНИК виконала студентка 52 МФІм групи Завальніцька Марія

Поняття про статистику Основні терміни та поняття статистики Види статистики Числові характеристики вибірки Математична статистика Полігон частот, гістограма. Статистичне спостереження Цікаві факти Перевір себе сам

Поняття про Статистику СТАТИСТИКАЦЕ НАУКА , ЯКА ВИВЧАЄ, ОБРОБЛЯЄ Й АНАЛІЗУЄ КІЛЬКІСНІ ДАНІ ПРО НАЙРІЗНОМАНІТНІШІ МАСОВІ ЯВИЩА В ЖИТТІ «Статистика знает все. Точно учтено количество пахотной земли с подразделением на чернозем, суглинок и лесс. Все граждане обоего пола записаны в аккуратные толстые книги-книги загсов. Известно, сколько какой пищи съедает в год средний гражданин республики. Известно, сколько в стране охотников, балерин, револьверных станков, собак всех пород, велосипедов, памятников, девушек, маяков и швейных машинок…. . » Остап Бендер. К/ф «Дванадцять стільців»

Види статистики Медична Економічна Демографічна Біологічна Податкова Фінансова Метереологічна

Статистика вчить, як проаналізувати інформацію, виявити та оцінити закономірності формування, розвитку та взаємодії складових за своєю природою соціально-економічних явищ. Економічна статистика вивчає зміну цін, попиту та пропозиції на товари, прогнозує зростання та падіння виробництва й споживання. Медична статистика вивчає ефективність різних ліків і методів лікування, ймовірність виникнення деякого захворювання, прогнозує поширення епідемій. А є ще статистика демографічна, фінансова, податкова, біологічна. . .

Математична статистика МАТЕМАТИЧНА СТАТИСТИКАЦЕ РОЗДІЛ МАТЕМАТИКИ , ЯКИЙ ВИВЧАЄ МАТЕМАТИЧНІ МЕТОДИ ОБРОБКИ Й ВИКОРИСТАННЯ СТАТИСТИЧНИХ ДАНИХ ДЛЯ НАУКОВИХ І ПРАКТИЧНИХ ВИСНОВКІВ

Дослідження методами математичної статистики застосовуються для прийняття рішень, прогнозування розвитку певних галузей господарства, плануванні й організації виробництва, контролі якості продукції тощо. Серед основних задач математичної статистики можна відзначити такі : 1) Оцінка ймовірності. 2) Оцінка закону розподілу. 3) Оцінка числових характеристик випадкової величини. 4) Перевірка статистичних гіпотез. Першим етапом будь-якого дослідження є збирання інформації, а саме, статистичне спостереження.

Математична статистика Опис даних Табличне подання даних Графічне подання даних Обробка даних Формулювання висновків

Статистичне спостереження – це спланований, науково організований збір масових даних про соціальноекономічні явища та процеси. Приклади статистичних спостережень: перепис населення; телефонне опитування та інші. Спостереження є суцільним, якщо обстежують ознаки всіх одиниць сукупності. Прикладом може бути медичне обстеження населення у зв'язку з епідемією. Спостереження є несуцільним, якщо обстежуються ознаки окремих одиниць сукупності. Найбільш поширеним видом несуцільного спостереження є вибіркове спостереження. Його застосовують тоді, коли в сукупність 2 входить дуже велика кількість об'єктів або спостереження пов'язане із руйнуванням об'єктів, або ж воно вимагає великих затрат. У таких випадках зі всієї сукупності вибирають обмежену кількість об'єктів і вивчають їх.

Основні терміни та поняття статистики Генеральна сукупність Множина всіх можливих результатів спостереження ( вимірювання) Статистична Множина результатів, які реально вибірка, статистич одержані в даному спостереженні ний ряд ( вимірюванні) Варіанта Одне із значень елементів вибірки Варіаційний ряд Упорядкована множина всіх варіант

Числові характеристики вибірки РОЗМАХ ВИБІРКИ Різниця між найбільшим і найменшим значеннями величини у вибірці МОДА ВИБІРКИ Значення елемента вибірки, яке зустрічається частіше за інші МЕДІАНА ВИБІРКИ Це серединне значення впорядкованого ряду значень випадкової величини Медiана (у статистицi) — варiанта, яка розмiщена посерединi варiацiйного ряду (у випадку непарної кiлькостi варiант), або є середнiм арифметичним двох середнiх членiв (якщо кiлькiсть варiант парна). СЕРЕДНЄ ЗНАЧЕННЯ ВИБІРКИ Середнє арифметичне всіх чисел ряду даної вибірки

Розглянемо дані поняття на прикладі У відділі жіночого взуття протягом трьох днів було проведено обстеження для вивчення попиту на певні розміри взуття. За ці дні було продано 14 пар взуття 37, 38, 39, 40 і 41 розмірів.

Запишемо № розміру взуття і кількість відповідних йому проданих пар в таблицю № взуття 37 38 39 40 41 варіанти Кількість проданих пар обуві 3 5 3 2 1 частота варіант 6/14 5/14 3/14 2/14 1/14 відносна частота варіант Відношення кількості проданих пар даного номеру до кількості всіх проданих пар Генеральна сукупність - кількість всіх пар обуві в магазині Вибірка- 14 пар обуві 37, 37, 38, 38, 38, 39, 39, 40, 41 - статистичний, ранжований ряд.

Обчислимо числові характеристики вибірки 37, 37, 38, 38, 38, 39, 39, 40, 41 - вибірка Об’єм вибірки: 14 Розмах вибірки: 41 -37=4 Мода вибірки: 38 Медіана вибірки: 38 Середнє значення : (37+37+37+38+38+39+39+39+40+40+41): 14=

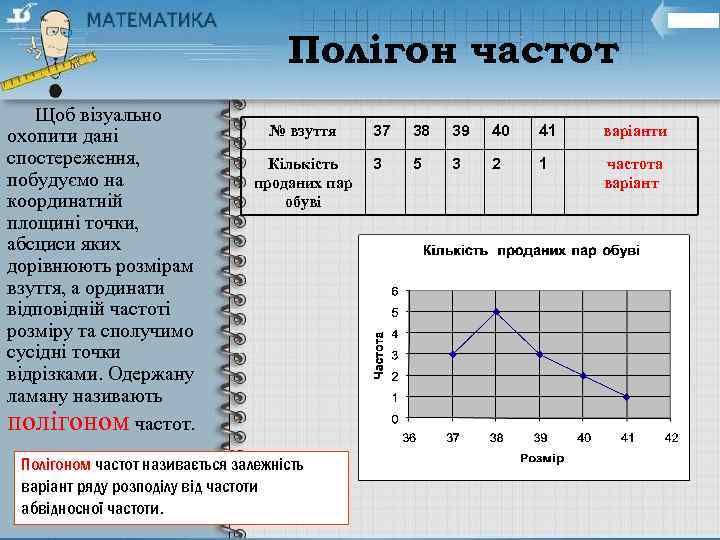Полігон частот Щоб візуально охопити дані спостереження, побудуємо на координатній площині точки, абсциси яких дорівнюють розмірам взуття, а ординати відповідній частоті розміру та сполучимо сусідні точки відрізками. Одержану ламану називають полігоном частот. № взуття 37 38 39 40 41 варіанти Кількість проданих пар обуві 3 5 3 2 1 частота варіант Полігоном частот називається залежність варіант ряду розподілу від частоти абвідносної частоти.

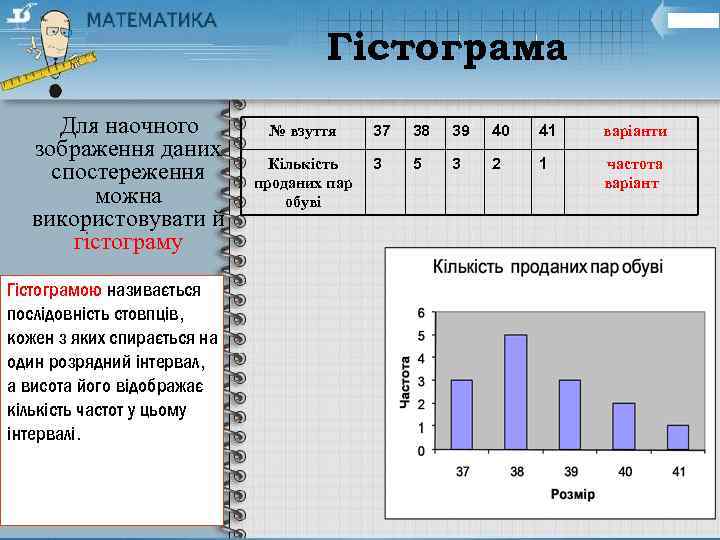Гістограма Для наочного зображення даних спостереження можна використовувати й гістограму Гістограмою називається послідовність стовпців, кожен з яких спирається на один розрядний інтервал, а висота його відображає кількість частот у цьому інтервалі. № взуття 37 38 39 40 41 варіанти Кількість проданих пар обуві 3 5 3 2 1 частота варіант

Цікаві факти даних статистики (здоров’я): За статистичними даними та результатами опитування серед учнівської молоді шкідливими звичками уражено від 0 до 74% юнаків та дівчат віком 17 -18 років. У 60 % випускників шкіл встановлено хронічні захворювання.

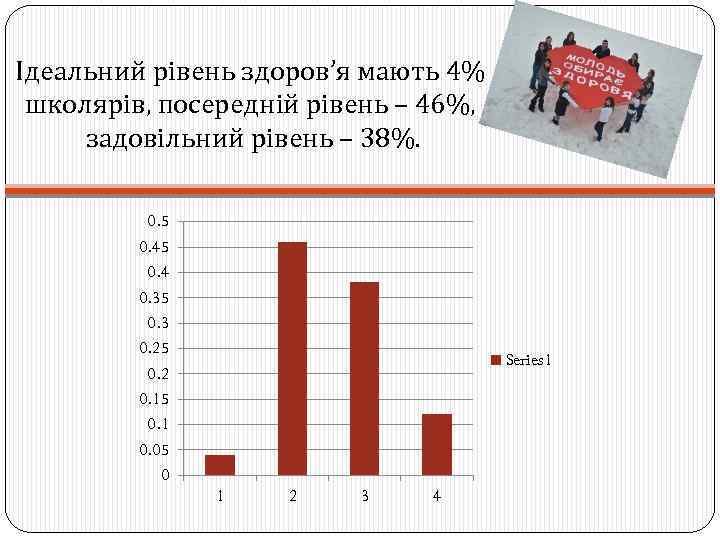Ідеальний рівень здоров’я мають 4% школярів, посередній рівень – 46%, задовільний рівень – 38%. 0. 5 0. 4 0. 35 0. 3 0. 25 0. 2 0. 15 0. 1 0. 05 0 Series 1 1 2 3 4

Серед хворих на рак 95% курців, зі 100 випадків захворювання на туберкульоз 95% припадають на курців. ***** У новонародженого частка води становить 85% маси тіла, у юнаків – у середньому 63%, у дівчат – 52%. ***** Регулярно виконують ранкову гімнастику 6% студентів, 18% курсантів, ніколи не виконують – 74%, і 24% – курсантів.

Задача. ПРИ ОПИТУВАННІ ДВАДЦЯТЬОХ УЧНІВ ШКОЛИ БУЛО ВИЯВЛЕНО, ЩО 7 УЧНІВ ЛЮБЛЯТЬ ПРЕДМЕТ ФІЗКУЛЬТУРУ, 5 УЧНІВ-МАТЕМАТИКУ, 4 УЧНІ-ІСТОРІЮ , 3 УЧНІ-БІОЛОГІЮ, 1 УЧЕНЬ-ХІМІЮ. ВИЗНАЧИТИ ГЕНЕРАЛЬНУ СУКУПНІСТЬ, ВИБІРКУ, ВАРІАНТИ ВИБІРКИ ТА ЧАСТОТУ ВАРІАНТ.

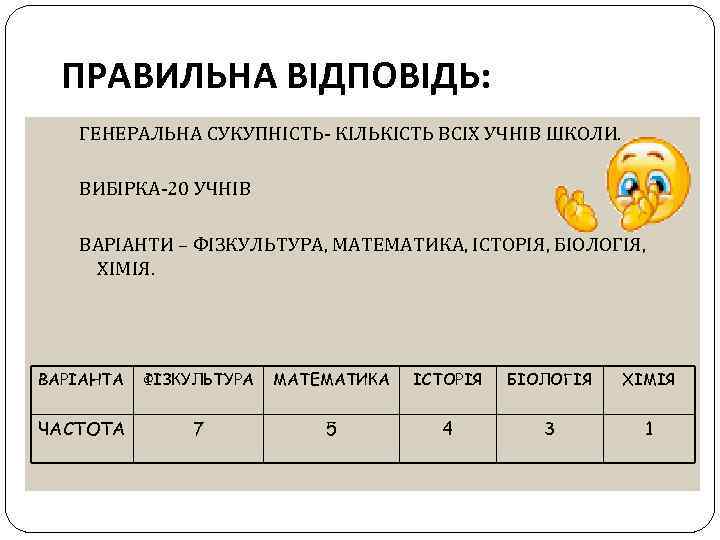ПРАВИЛЬНА ВІДПОВІДЬ: ГЕНЕРАЛЬНА СУКУПНІСТЬ- КІЛЬКІСТЬ ВСІХ УЧНІВ ШКОЛИ. ВИБІРКА-20 УЧНІВ ВАРІАНТИ – ФІЗКУЛЬТУРА, МАТЕМАТИКА, ІСТОРІЯ, БІОЛОГІЯ, ХІМІЯ. ВАРІАНТА ФІЗКУЛЬТУРА МАТЕМАТИКА ІСТОРІЯ БІОЛОГІЯ ХІМІЯ ЧАСТОТА 7 5 4 3 1

Виконання вправ: Вправа 1. Учні 9 класу підготували вибірку з даних свого класу: рік народження, стать і рівень досягнень знань. Побудувати діаграму. Проаналізувати графік. Знайти центральні тенденції: моду, медіану і середнє значення вибірки.

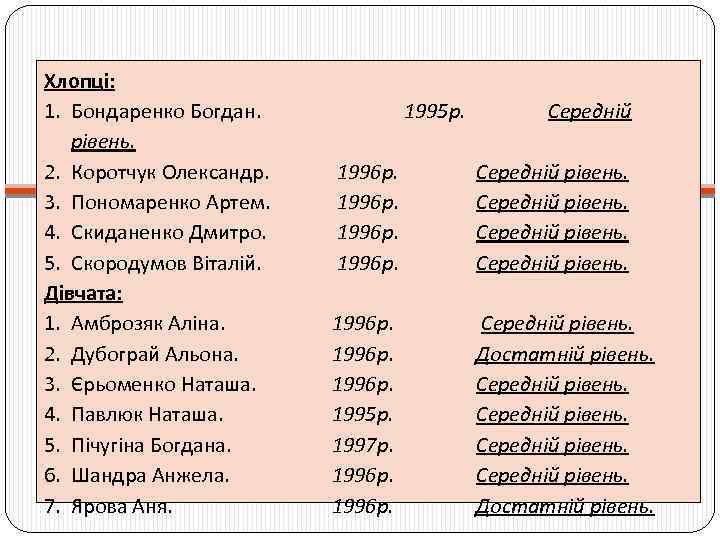Хлопці: 1. Бондаренко Богдан. рівень. 2. Коротчук Олександр. 3. Пономаренко Артем. 4. Скиданенко Дмитро. 5. Скородумов Віталій. Дівчата: 1. Амброзяк Аліна. 2. Дубограй Альона. 3. Єрьоменко Наташа. 4. Павлюк Наташа. 5. Пічугіна Богдана. 6. Шандра Анжела. 7. Ярова Аня. 1995 р. Середній 1996 р. Середній рівень. 1996 р. 1995 р. 1997 р. 1996 р. Середній рівень. Достатній рівень.

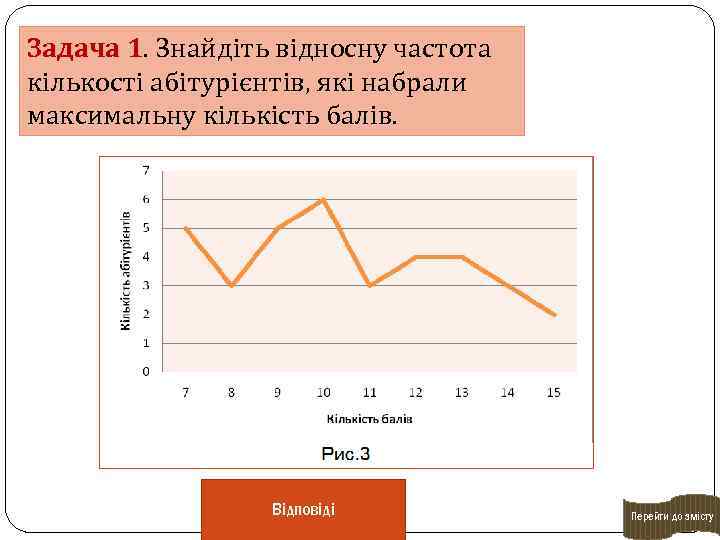Задача 1. Знайдіть відносну частота кількості абітурієнтів, які набрали максимальну кількість балів. Відповіді Перейти до змісту

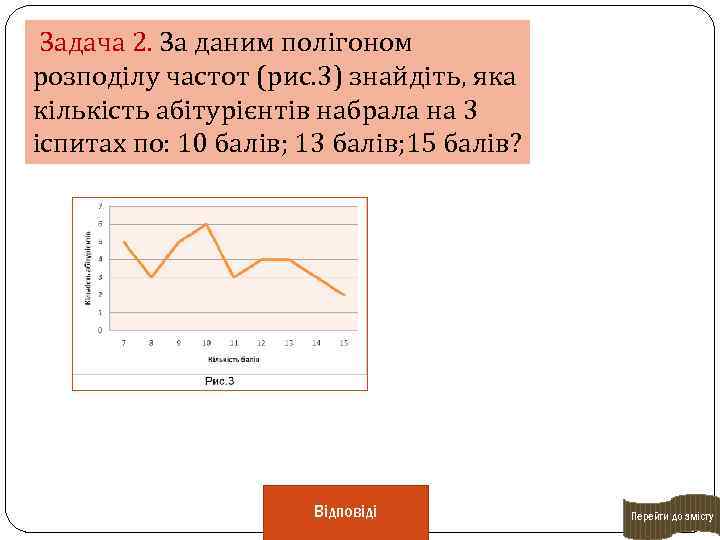Задача 2. За даним полігоном розподілу частот (рис. 3) знайдіть, яка кількість абітурієнтів набрала на 3 іспитах по: 10 балів; 13 балів; 15 балів? Відповіді Перейти до змісту

4. Дано вибірку 14, 16, 13, 17, 3. Дано вибірку 6, 9, 8, 7, 5, 4, 4, 32, 9, 8, 4, 1. Знайти моду, медіану і середнє значення вибірки. Побудувати 14, 18, 17, 19, 14. Знайти моду, медіану і середнє значення вибірки. Побудувати гістограму. Відповіді Перейти до змісту

1. Відповідь: ( 2 /35) Повенутися до завдань Перейти до змісту

3. (Відповідь: мода – 4, медіана – (6+7)/2=6, 5; середнє значення – 8, 08). 4. (Відповідь: мода – 14, медіана – 16, середнє значення – 15, 7). Повернутися до завдань

2. Відповідь: (6; 4; 2) Повернутися до завдань

Перейти до змісту