Microfluidic Applications of Magnetic and Dielectric Fluid Suspensions

Microfluidic Applications of Magnetic and Dielectric Fluid Suspensions Markus Zahn Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Research Laboratory of Electronics Laboratory for Electromagnetic and Electronic Systems High Voltage Research Laboratory Hsin-Fu Huang National Taiwan University Department of Mechanical Engineering Research Workshop of the Israel Science Foundation on Electrokinetic Phenomena in Nano-colloids and Nano-Fluidics Technion-Israel Institute of Technology Haifa, Israel 19 -23 December 2010 1

OUTLINE 1. Introduction to Ferrohydrodynamics 2. Applications to Magnetic Resonance Imaging (MRI) 3. Ferrohydrodynamic Instabilities 4. Dielectric Analog: Von Quincke Electrorotation 5. Use of Micro-particle Electrorotation in Enhancing the Macroscopic Suspension Flow Rate 6. Continuum Analysis of Poiseuille Flow with 2

1. INTRODUCTION TO FERRODYNAMICS FERROHYDRODYNAMIC S (Linear Magnetization) (Force Density) (Magnetizable Medium) (Magnetic Diffusion Time) (Skin Depth) (Magnetic Reynolds Number) ELECTROHYDRODYNA (Linear Dielectric) MICS (Force Density) (Polarizable Dielectric) (Dielectric Relaxation Time) (Electric Reynolds Number) 3

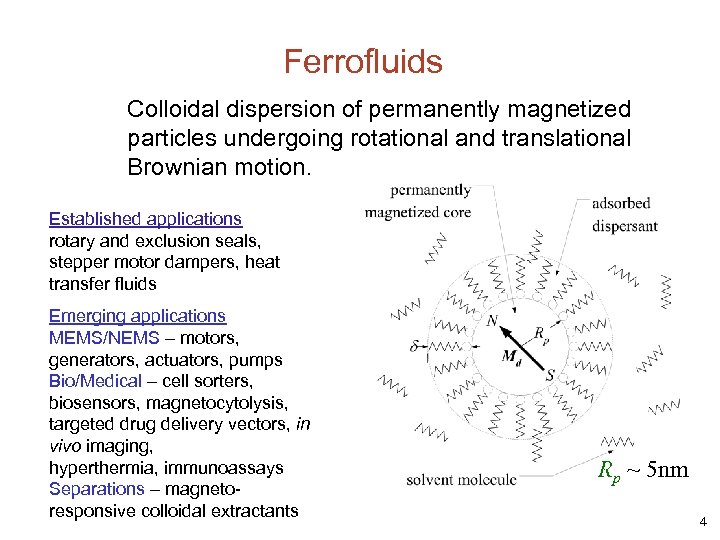Ferrofluids Colloidal dispersion of permanently magnetized particles undergoing rotational and translational Brownian motion. Established applications rotary and exclusion seals, stepper motor dampers, heat transfer fluids Emerging applications MEMS/NEMS – motors, generators, actuators, pumps Bio/Medical – cell sorters, biosensors, magnetocytolysis, targeted drug delivery vectors, in vivo imaging, hyperthermia, immunoassays Separations – magnetoresponsive colloidal extractants Rp ~ 5 nm 4

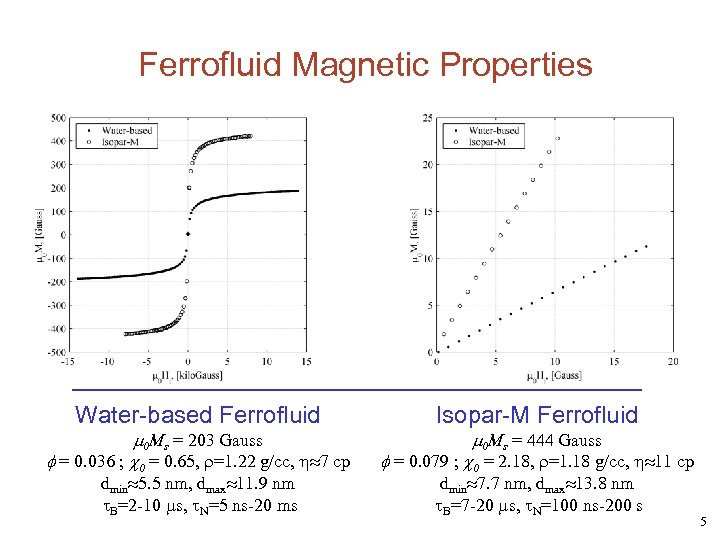Ferrofluid Magnetic Properties Water-based Ferrofluid m 0 Ms = 203 Gauss f = 0. 036 ; c 0 = 0. 65, =1. 22 g/cc, 7 cp dmin 5. 5 nm, dmax 11. 9 nm B=2 -10 s, N=5 ns-20 ms Isopar-M Ferrofluid m 0 Ms = 444 Gauss f = 0. 079 ; c 0 = 2. 18, =1. 18 g/cc, 11 cp dmin 7. 7 nm, dmax 13. 8 nm B=7 -20 s, N=100 ns-200 s 5

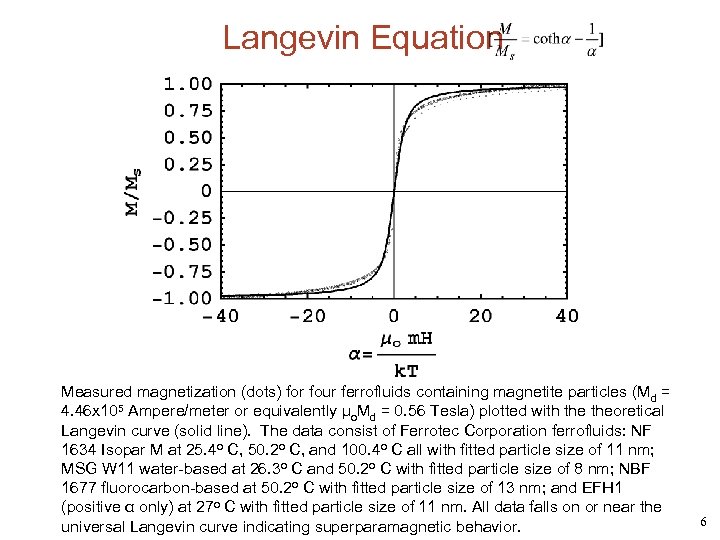Langevin Equation Measured magnetization (dots) for four ferrofluids containing magnetite particles (Md = 4. 46 x 105 Ampere/meter or equivalently μo. Md = 0. 56 Tesla) plotted with theoretical Langevin curve (solid line). The data consist of Ferrotec Corporation ferrofluids: NF 1634 Isopar M at 25. 4 o C, 50. 2 o C, and 100. 4 o C all with fitted particle size of 11 nm; MSG W 11 water-based at 26. 3 o C and 50. 2 o C with fitted particle size of 8 nm; NBF 1677 fluorocarbon-based at 50. 2 o C with fitted particle size of 13 nm; and EFH 1 (positive α only) at 27 o C with fitted particle size of 11 nm. All data falls on or near the universal Langevin curve indicating superparamagnetic behavior. 6

Ferrofluid Magnetization Force A magnetizable liquid is drawn upward around a currentcarrying wire. 7

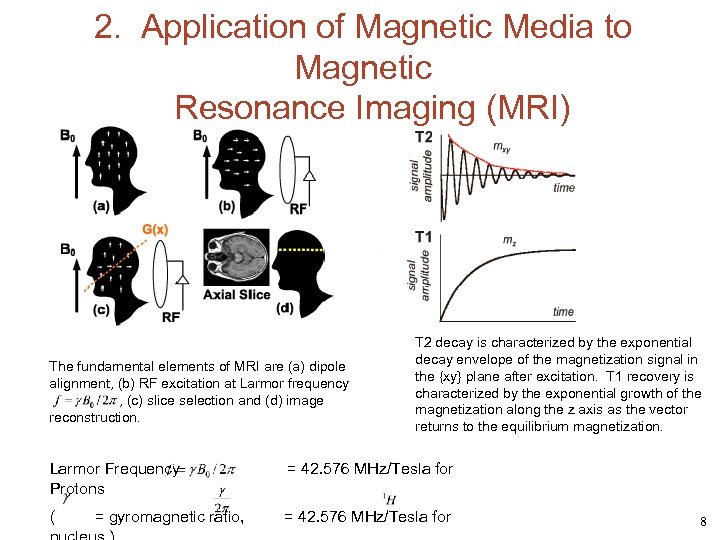2. Application of Magnetic Media to Magnetic Resonance Imaging (MRI) The fundamental elements of MRI are (a) dipole alignment, (b) RF excitation at Larmor frequency , (c) slice selection and (d) image reconstruction. T 2 decay is characterized by the exponential decay envelope of the magnetization signal in the {xy} plane after excitation. T 1 recovery is characterized by the exponential growth of the magnetization along the z axis as the vector returns to the equilibrium magnetization. Larmor Frequency Protons = 42. 576 MHz/Tesla for ( = 42. 576 MHz/Tesla for = gyromagnetic ratio, 8

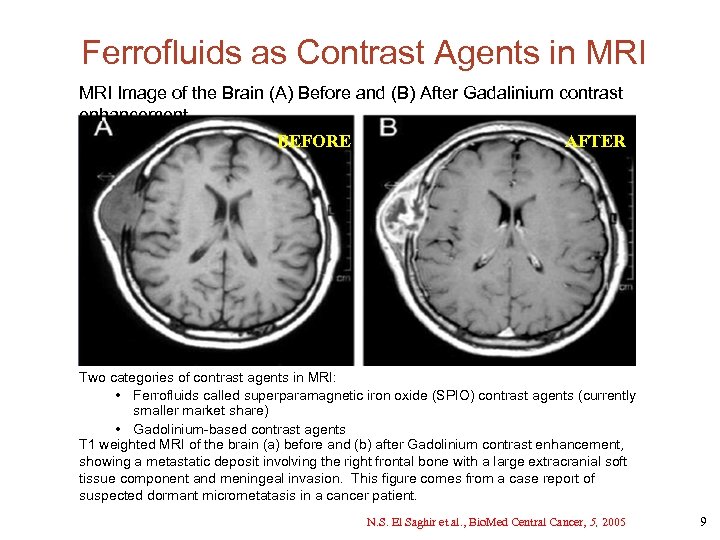Ferrofluids as Contrast Agents in MRI Image of the Brain (A) Before and (B) After Gadalinium contrast enhancement BEFORE AFTER Two categories of contrast agents in MRI: • Ferrofluids called superparamagnetic iron oxide (SPIO) contrast agents (currently smaller market share) • Gadolinium-based contrast agents T 1 weighted MRI of the brain (a) before and (b) after Gadolinium contrast enhancement, showing a metastatic deposit involving the right frontal bone with a large extracranial soft tissue component and meningeal invasion. This figure comes from a case report of suspected dormant micrometatasis in a cancer patient. N. S. El Saghir et al. , Bio. Med Central Cancer, 5, 2005 9

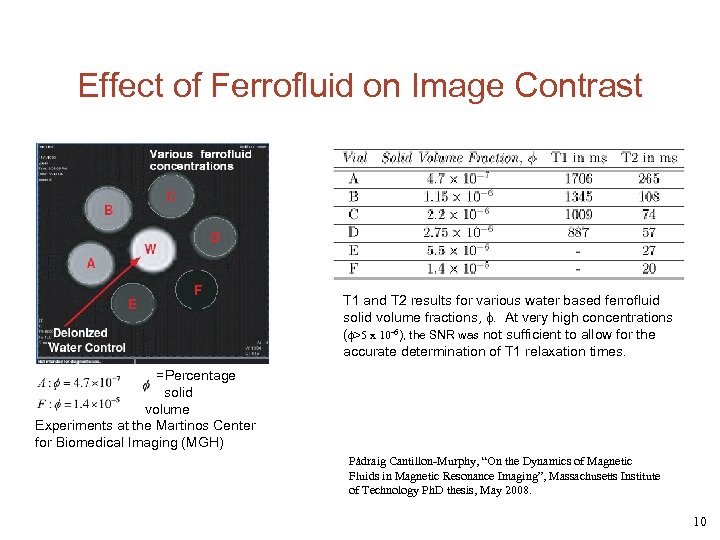Effect of Ferrofluid on Image Contrast T 1 and T 2 results for various water based ferrofluid solid volume fractions, . At very high concentrations ( >5 x 10 -6), the SNR was not sufficient to allow for the accurate determination of T 1 relaxation times. =Percentage solid volume Experiments at the Martinos Center for Biomedical Imaging (MGH) Pádraig Cantillon-Murphy, “On the Dynamics of Magnetic Fluids in Magnetic Resonance Imaging”, Massachusetts Institute of Technology Ph. D thesis, May 2008. 10

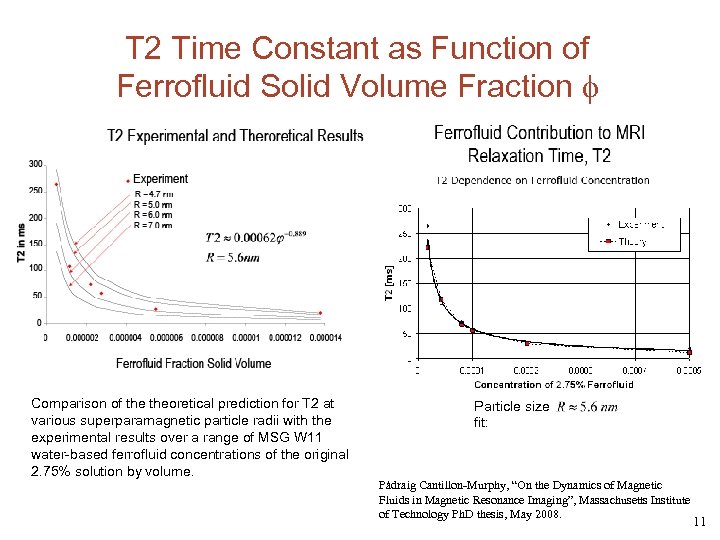T 2 Time Constant as Function of Ferrofluid Solid Volume Fraction Comparison of theoretical prediction for T 2 at various superparamagnetic particle radii with the experimental results over a range of MSG W 11 water-based ferrofluid concentrations of the original 2. 75% solution by volume. Particle size fit: Pádraig Cantillon-Murphy, “On the Dynamics of Magnetic Fluids in Magnetic Resonance Imaging”, Massachusetts Institute of Technology Ph. D thesis, May 2008. 11

Conservation of Linear and Angular Momentum M = Nm N = num. particles per m 3 ζ = vortex viscosity – Viscous dominated regime – Particle spin-velocity is no longer given by vorticity – Magnetic torque density in Con of Ang Mom: 12

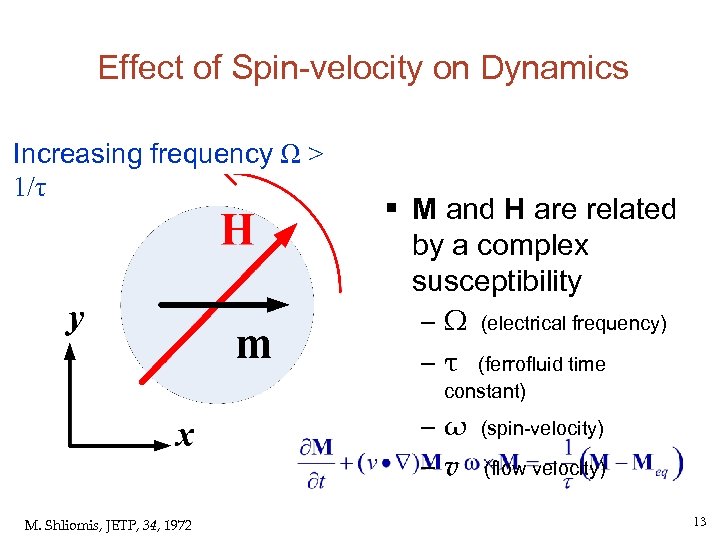Effect of Spin-velocity on Dynamics Increasing frequency Ω > 1/τ § M and H are related by a complex susceptibility –Ω –τ (electrical frequency) (ferrofluid time constant) –ω –v M. Shliomis, JETP, 34, 1972 (spin-velocity) (flow velocity) 13

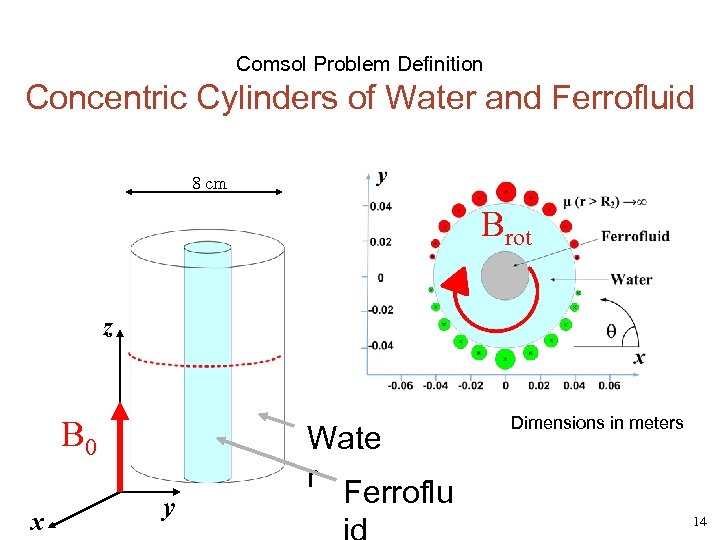Comsol Problem Definition Concentric Cylinders of Water and Ferrofluid 8 cm Brot z B 0 x y Wate r Ferroflu Dimensions in meters 14

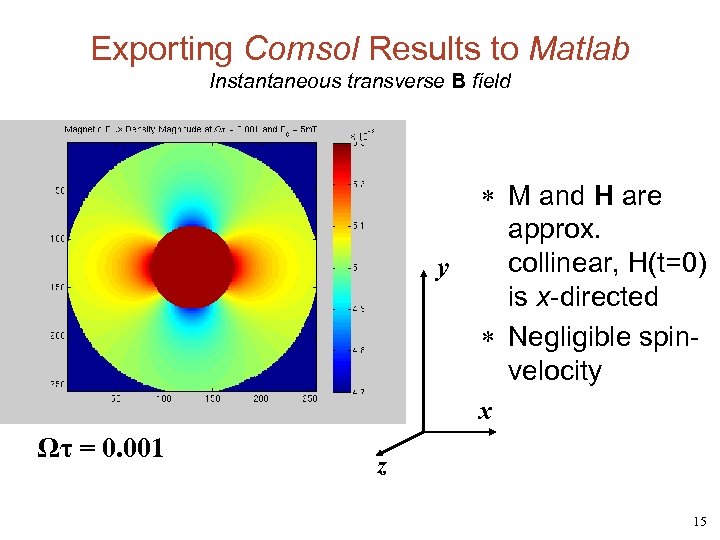Exporting Comsol Results to Matlab Instantaneous transverse B field y * M and H are approx. collinear, H(t=0) is x-directed * Negligible spinvelocity x Ωτ = 0. 001 z 15

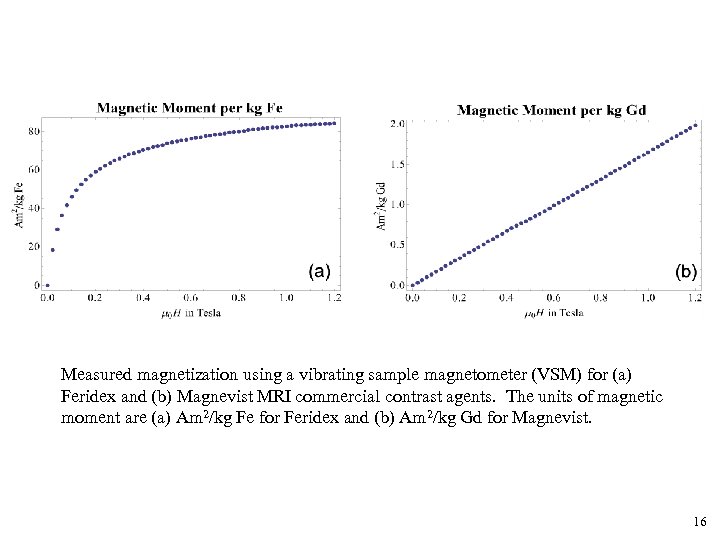Measured magnetization using a vibrating sample magnetometer (VSM) for (a) Feridex and (b) Magnevist MRI commercial contrast agents. The units of magnetic moment are (a) Am 2/kg Fe for Feridex and (b) Am 2/kg Gd for Magnevist. 16

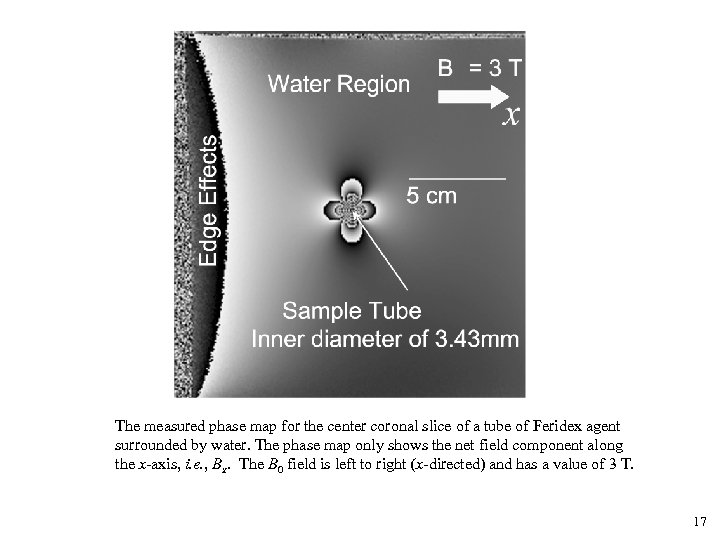The measured phase map for the center coronal slice of a tube of Feridex agent surrounded by water. The phase map only shows the net field component along the x-axis, i. e. , Bx. The B 0 field is left to right (x-directed) and has a value of 3 T. 17

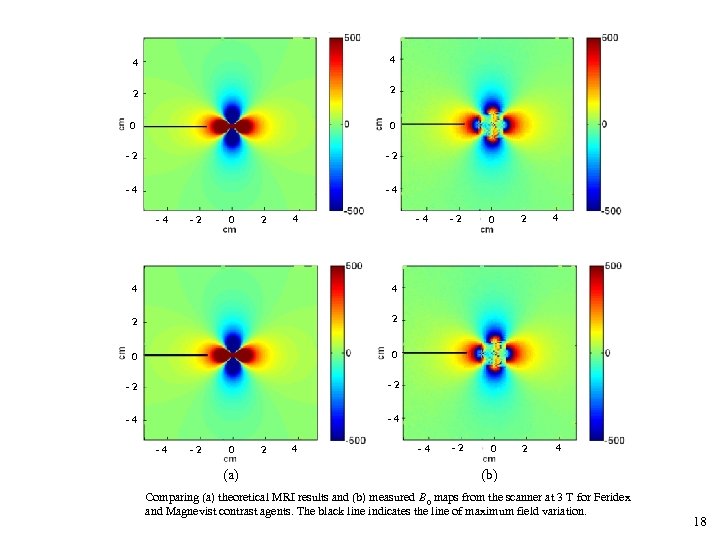4 4 2 2 0 0 - 2 - 4 - 4 - 2 0 2 - 4 4 4 - 2 0 2 4 - 2 - 4 4 0 - 2 2 2 0 0 4 2 - 4 - 2 0 (a) 2 4 (b) Comparing (a) theoretical MRI results and (b) measured B 0 maps from the scanner at 3 T for Feridex and Magnevist contrast agents. The black line indicates the line of maximum field variation. 18

3. Ferrohydrodynami c Instabilities In DC Magnetic Fields 19

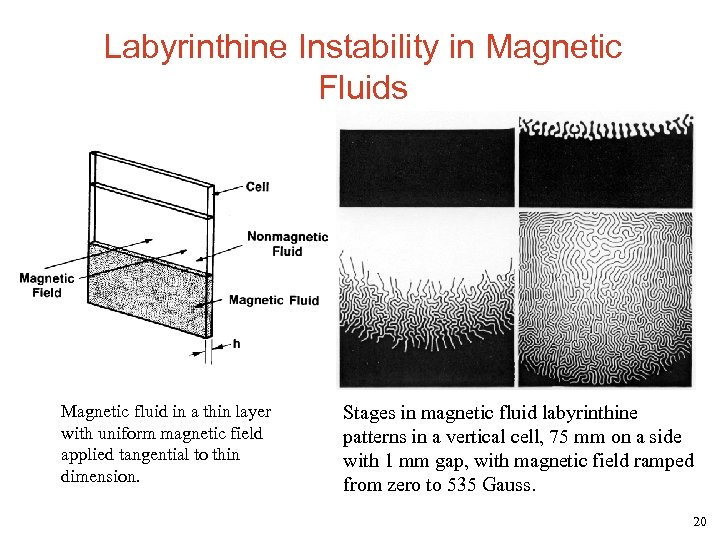Labyrinthine Instability in Magnetic Fluids Magnetic fluid in a thin layer with uniform magnetic field applied tangential to thin dimension. Stages in magnetic fluid labyrinthine patterns in a vertical cell, 75 mm on a side with 1 mm gap, with magnetic field ramped from zero to 535 Gauss. 20

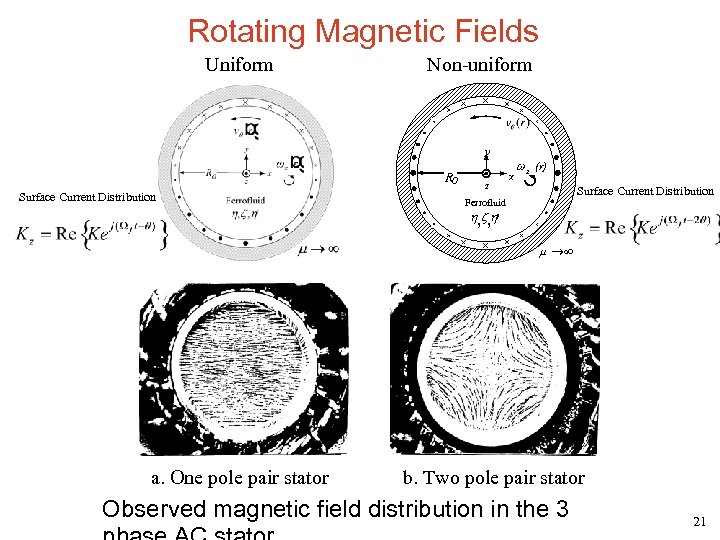Rotating Magnetic Fields Uniform Non-uniform y RO Surface Current Distribution z x w z (r) Surface Current Distribution Ferrofluid h, z , h' m ®¥ a. One pole pair stator b. Two pole pair stator Observed magnetic field distribution in the 3 21

Ferrofluid Drops in Rotating Magnetic Fields A Gallery of Instabilities Ferrohydrodynamic Drops 22

Ferrofluid Spiral / Phase Transformations 23

4. Dielectric Analog: Von Quincke’s Rotor (Electrorotation) Von Quincke’s Rotor (a) Von Quincke’s rotor consists of a highly insulating cylinder that is free to rotate and that is placed in slightly conducting oil between parallel plate electrodes. As DC high voltage is raised, at a critical voltage the cylinder spontaneously rotates in either direction; (b) The motion occurs because the insulating rotor charges like a capacitor with positive surface charge near the positive electrode and negative surface charge near the negative electrode. Any slight rotation of the cylinder in either direction results in an electrical torque in the same direction as the initial displacement. 24

More on Quincke’s Rotor (Electrorotation) Definition of Quincke Rotation: Spontaneous rotation of insulating particles (or cylinders) suspended in a slightly conducting liquid subjected to a DC electric field with the field strength exceeding some critical value (Jones, 1984, 1995) when where is the charge relaxation time in each region Two Competing Forces (Torques): The electrical torque and the fluid viscous torque exerted on the particle 25

Torques Exerted on a Micro-particle The fluid viscous torque The electric torque For a small perturbation of rotation to grow, the equation of angular motion for the particle is re-written as (Jones, 1995): The bracket term should have a value larger than zero for the small perturbation to grow (Jones, 1995), thus 26

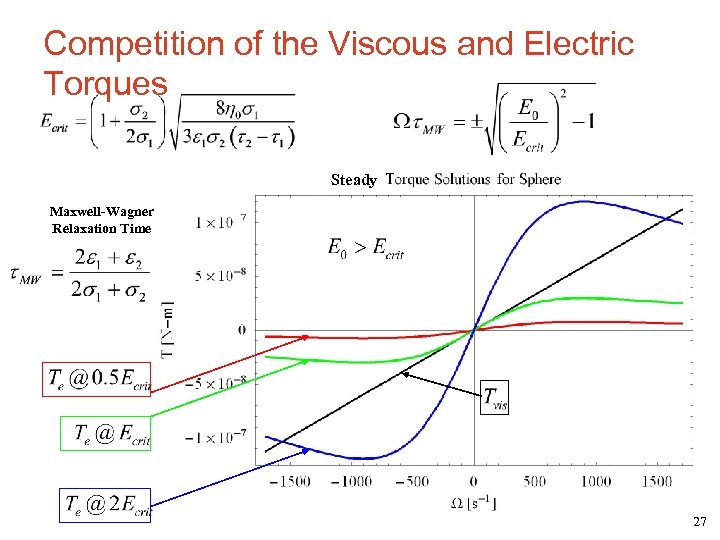Competition of the Viscous and Electric Torques Steady Maxwell-Wagner Relaxation Time 27

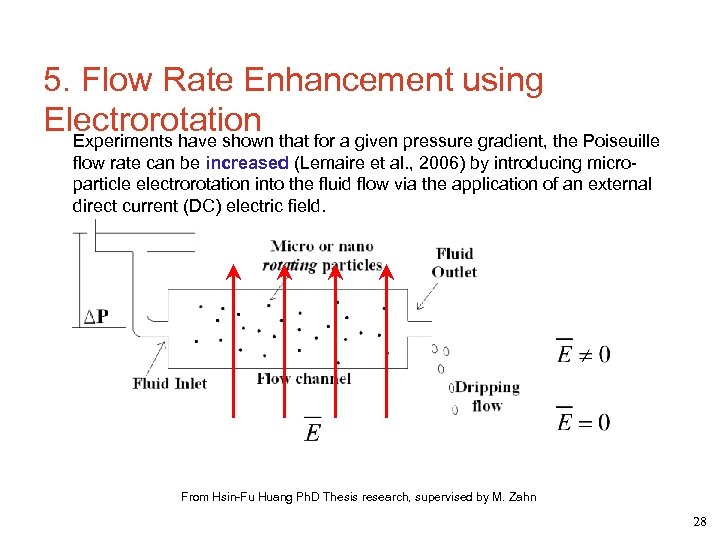5. Flow Rate Enhancement using Electrorotation that for a given pressure gradient, the Poiseuille Experiments have shown flow rate can be increased (Lemaire et al. , 2006) by introducing microparticle electrorotation into the fluid flow via the application of an external direct current (DC) electric field. From Hsin-Fu Huang Ph. D Thesis research, supervised by M. Zahn 28

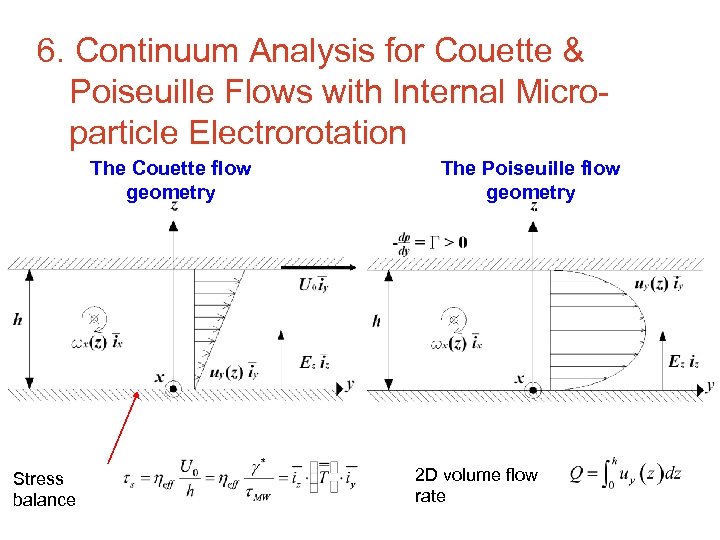6. Continuum Analysis for Couette & Poiseuille Flows with Internal Microparticle Electrorotation The Couette flow geometry Stress balance The Poiseuille flow geometry 2 D volume flow rate

The Continuum Governing Equations EQS & Electroneutrality (Haus & Melcher, 1989) Polarization Relaxation Equilibrium Polarization Particle # density Continuity Incompressible flow: treating as a single phase continuum Linear Momentum (Dahler & Scriven, 1961, 1963; Condiff & Dahler, 1964; Rosensweig, 1997) No-slip boundary conditions Zaitsev & Shliomis, (1969); Rosensweig, (1997) Angular Momentum (Dahler & Scriven, 1961, 1963; Condiff & Dahler, 1964; Rosensweig, 1997) Field conditions: free-to-spin, symmetry, stable rotation Lobry & Lemaire, 1999; He, 2006; Lemaire et al. , 2008 Spin field BCs: Kaloni, 1992; Lukaszewicz, 1999; Rinaldi, 2002; Rinaldi & Zahn,

Polarization Relaxation & Equilibrium Polarization Shliomis’ First Magnetization Relaxation Equation (1972, 2002) Cebers’ Dipole Relaxation Equation (1980) Debye form (Shliomis, 1972, 2002) + Dahler & Scriven (1963) We only relax the part of polarization directly related to the surface charges on the microparticles, i. e. , the retarding part of the fluid polarization instead of relaxing the whole total ER fluid polarization. Huang, (2010); Huang, Zahn, & Lemaire, (2010 a, b)

Polarization Relaxation & Equilibrium Electric potential and field solutions to a spherical particle subjected to a uniform Polarization at an angular velocity of. DC electric field rotating z r , BCs (Cebers, 1980; Melcher, 1981; Pannacci, 2006) R Laplace’s equation with spherical harmonics (Jackson, 1999) y , x The proposed “rotating coffee cup model” for the retarding polarization relaxation equations with its accompanying (quasi-static) equilibrium retarding polarization (Huang, 2010; Huang, Zahn, & Lemaire, 2010 a, b): Retaining macroscopic fluid spin Including microscopic particle rotation

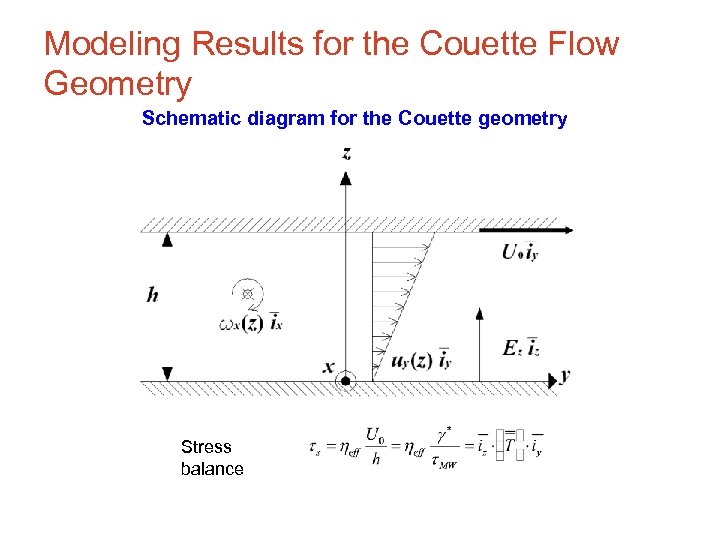Modeling Results for the Couette Flow Geometry Schematic diagram for the Couette geometry Stress balance

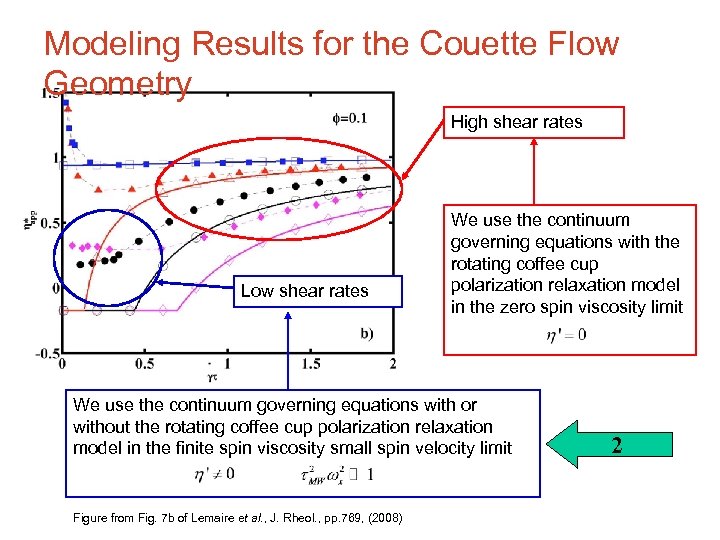
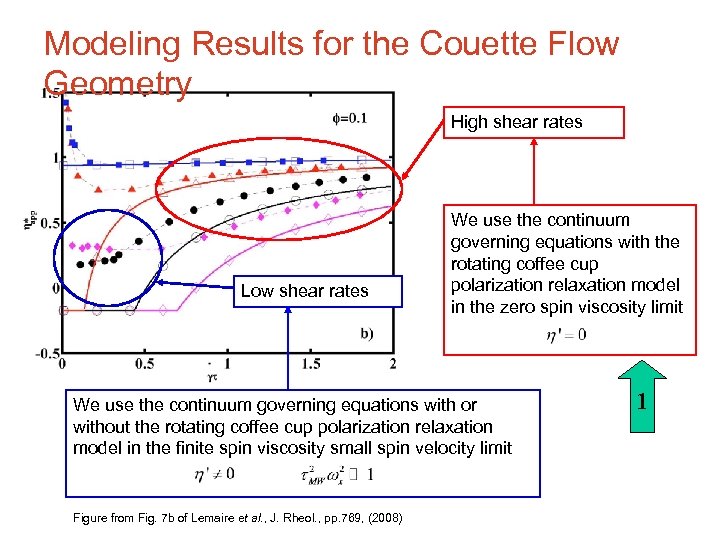Modeling Results for the Couette Flow Geometry High shear rates Low shear rates We use the continuum governing equations with the rotating coffee cup polarization relaxation model in the zero spin viscosity limit We use the continuum governing equations with or without the rotating coffee cup polarization relaxation model in the finite spin viscosity small spin velocity limit Figure from Fig. 7 b of Lemaire et al. , J. Rheol. , pp. 769, (2008) 1

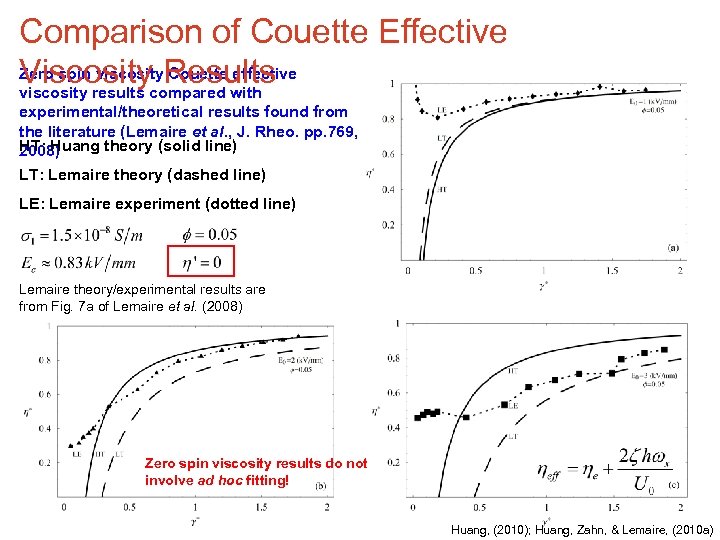Comparison of Couette Effective Zero spin viscosity. Results Couette effective Viscositycompared with viscosity results experimental/theoretical results found from the literature (Lemaire et al. , J. Rheo. pp. 769, HT: Huang theory (solid line) 2008) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) Lemaire theory/experimental results are from Fig. 7 a of Lemaire et al. (2008) Zero spin viscosity results do not involve ad hoc fitting! Huang, (2010); Huang, Zahn, & Lemaire, (2010 a)

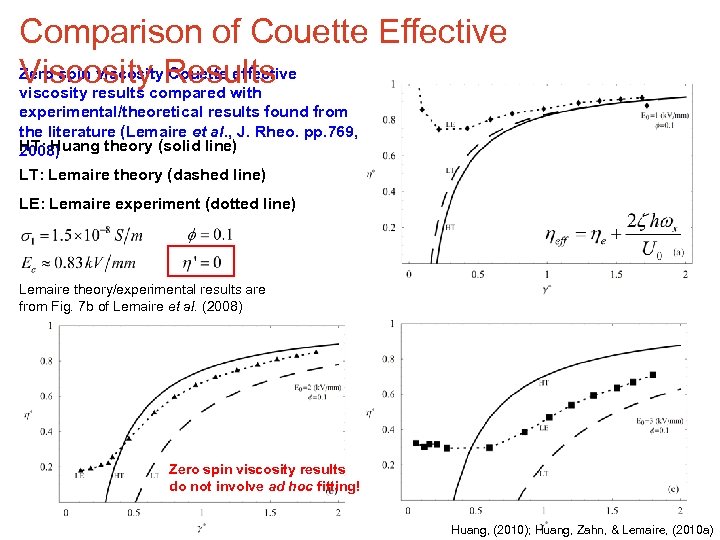Comparison of Couette Effective Zero spin viscosity. Results Couette effective Viscositycompared with viscosity results experimental/theoretical results found from the literature (Lemaire et al. , J. Rheo. pp. 769, HT: Huang theory (solid line) 2008) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) Lemaire theory/experimental results are from Fig. 7 b of Lemaire et al. (2008) Zero spin viscosity results do not involve ad hoc fitting! Huang, (2010); Huang, Zahn, & Lemaire, (2010 a)

Modeling Results for the Couette Flow Geometry High shear rates Low shear rates We use the continuum governing equations with the rotating coffee cup polarization relaxation model in the zero spin viscosity limit We use the continuum governing equations with or without the rotating coffee cup polarization relaxation model in the finite spin viscosity small spin velocity limit Figure from Fig. 7 b of Lemaire et al. , J. Rheol. , pp. 769, (2008) 2

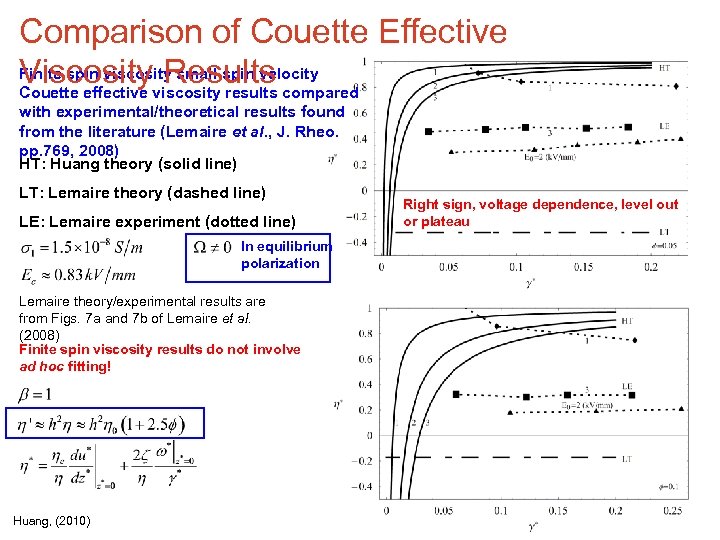Comparison of Couette Effective Finite spin viscosity small spin velocity Viscosityviscosity results compared Results Couette effective with experimental/theoretical results found from the literature (Lemaire et al. , J. Rheo. pp. 769, 2008) HT: Huang theory (solid line) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) In equilibrium polarization Lemaire theory/experimental results are from Figs. 7 a and 7 b of Lemaire et al. (2008) Finite spin viscosity results do not involve ad hoc fitting! Huang, (2010) Right sign, voltage dependence, level out or plateau

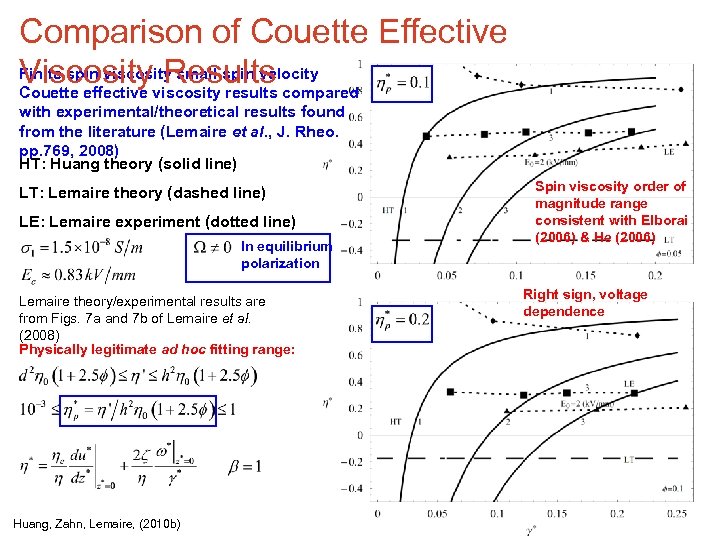Comparison of Couette Effective Finite spin viscosity small spin velocity Viscosityviscosity results compared Results Couette effective with experimental/theoretical results found from the literature (Lemaire et al. , J. Rheo. pp. 769, 2008) HT: Huang theory (solid line) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) In equilibrium polarization Lemaire theory/experimental results are from Figs. 7 a and 7 b of Lemaire et al. (2008) Physically legitimate ad hoc fitting range: Huang, Zahn, Lemaire, (2010 b) Spin viscosity order of magnitude range consistent with Elborai (2006) & He (2006) Right sign, voltage dependence

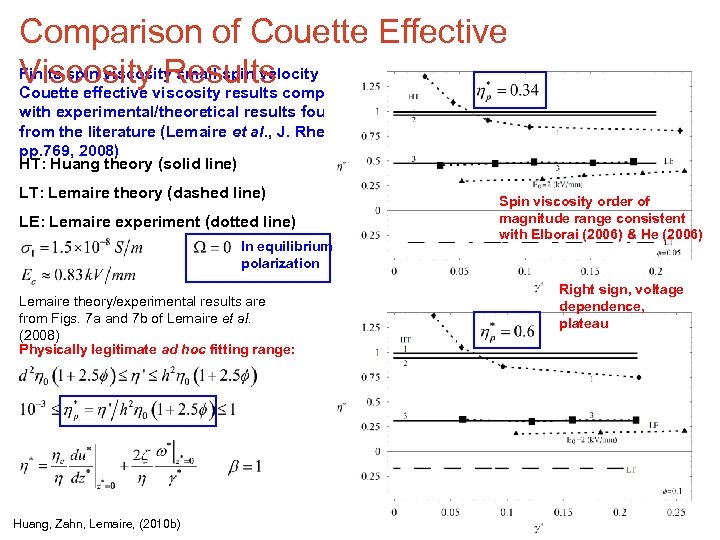Comparison of Couette Effective Finite spin viscosity small spin velocity Viscosityviscosity results compared Results Couette effective with experimental/theoretical results found from the literature (Lemaire et al. , J. Rheo. pp. 769, 2008) HT: Huang theory (solid line) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) In equilibrium polarization Lemaire theory/experimental results are from Figs. 7 a and 7 b of Lemaire et al. (2008) Physically legitimate ad hoc fitting range: Huang, Zahn, Lemaire, (2010 b) Spin viscosity order of magnitude range consistent with Elborai (2006) & He (2006) Right sign, voltage dependence, plateau

Modeling Results for the Poiseuille Flow Geometry Schematic diagram for the Poiseuille geometry 2 D volume flow rate

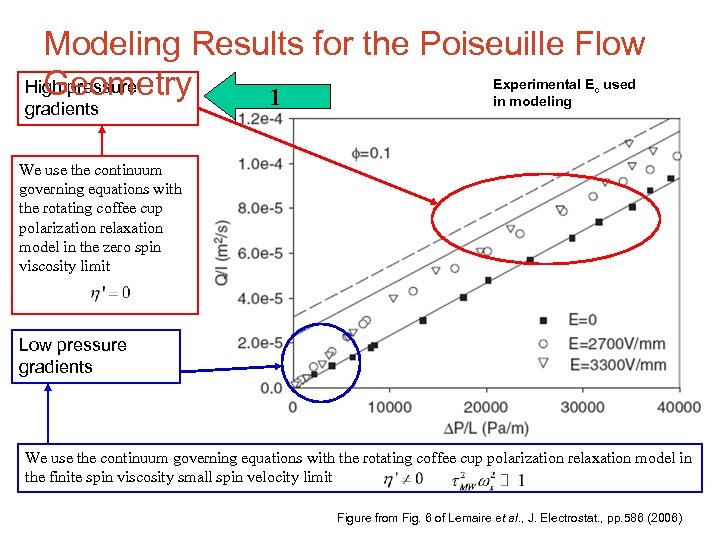Modeling Results for the Poiseuille Flow Experimental E used High pressure Geometry 1 in modeling c gradients We use the continuum governing equations with the rotating coffee cup polarization relaxation model in the zero spin viscosity limit Low pressure gradients We use the continuum governing equations with the rotating coffee cup polarization relaxation model in the finite spin viscosity small spin velocity limit Figure from Fig. 6 of Lemaire et al. , J. Electrostat. , pp. 586 (2006)

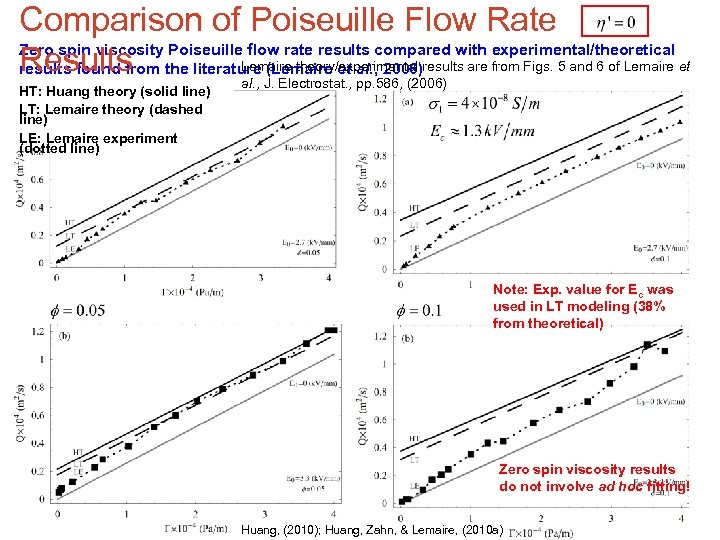Comparison of Poiseuille Flow Rate Zero spin viscosity Poiseuille flow rate results compared with experimental/theoretical Lemaire theory/experimental Results the literature J. Electrostat. , al. , 2006)results are from Figs. 5 and 6 of Lemaire et results found from (Lemaire et al. , pp. 586, (2006) HT: Huang theory (solid line) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) Note: Exp. value for Ec was used in LT modeling (38% from theoretical) Zero spin viscosity results do not involve ad hoc fitting! Huang, (2010); Huang, Zahn, & Lemaire, (2010 a)

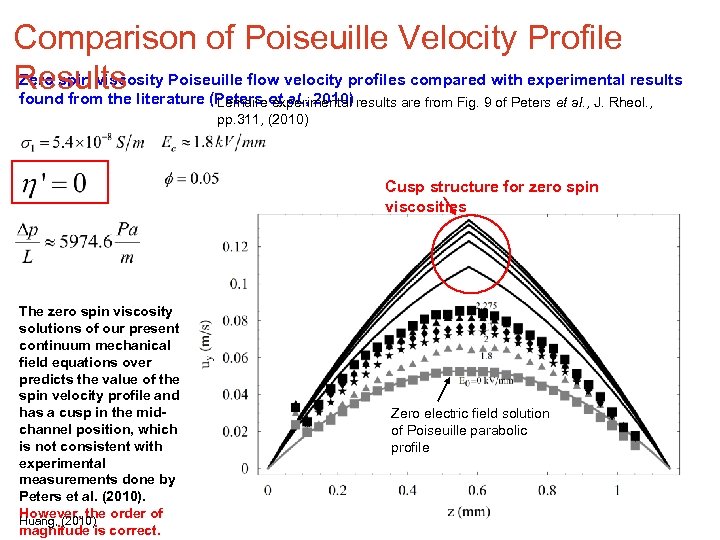Comparison of Poiseuille Velocity Profile Zero spin viscosity Poiseuille flow Results literature (Peters et velocity profiles compared with experimental results found from the al. , 2010) Lemaire experimental results are from Fig. 9 of Peters et al. , J. Rheol. , pp. 311, (2010) Cusp structure for zero spin viscosities The zero spin viscosity solutions of our present continuum mechanical field equations over predicts the value of the spin velocity profile and has a cusp in the midchannel position, which is not consistent with experimental measurements done by Peters et al. (2010). However, the order of Huang, (2010) magnitude is correct. Zero electric field solution of Poiseuille parabolic profile

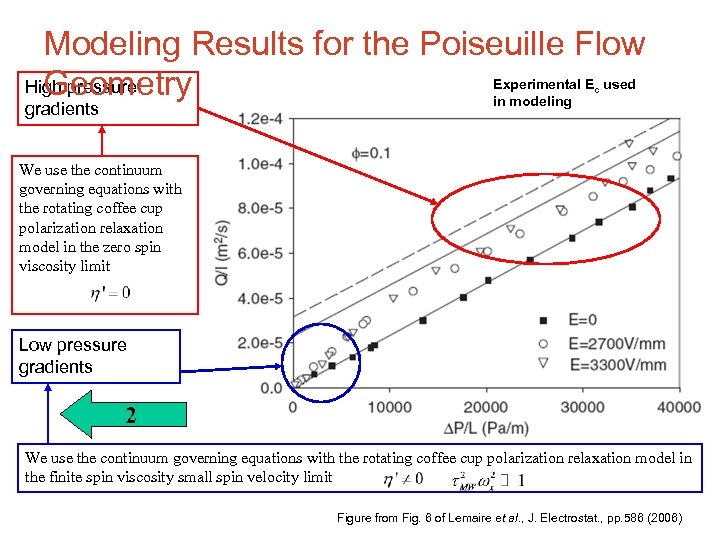Modeling Results for the Poiseuille Flow Experimental E used High pressure Geometry in modeling c gradients We use the continuum governing equations with the rotating coffee cup polarization relaxation model in the zero spin viscosity limit Low pressure gradients 2 We use the continuum governing equations with the rotating coffee cup polarization relaxation model in the finite spin viscosity small spin velocity limit Figure from Fig. 6 of Lemaire et al. , J. Electrostat. , pp. 586 (2006)

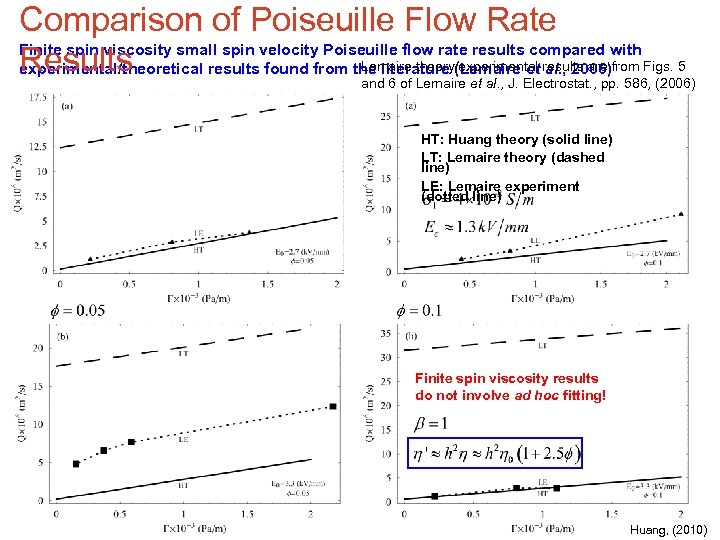Comparison of Poiseuille Flow Rate Finite spin viscosity small spin velocity Poiseuille flow rate results compared with Lemaire theory/experimental al. , 2006) Results experimental/theoretical results found from the literature (Lemaire et results are from Figs. 5 and 6 of Lemaire et al. , J. Electrostat. , pp. 586, (2006) HT: Huang theory (solid line) LT: Lemaire theory (dashed line) LE: Lemaire experiment (dotted line) Finite spin viscosity results do not involve ad hoc fitting! Huang, (2010)

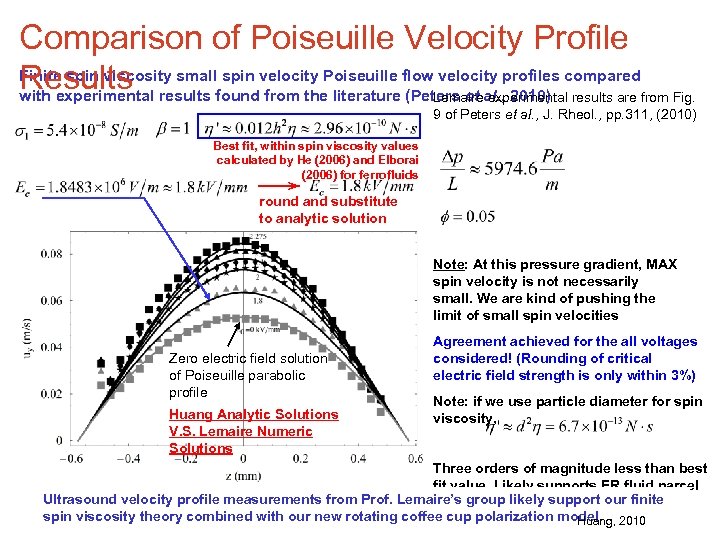Comparison of Poiseuille Velocity Profile Finite spin viscosity small spin velocity Poiseuille flow velocity profiles compared Results results found from the literature (Peters et al. , 2010) results are from Fig. with experimental Lemaire experimental 9 of Peters et al. , J. Rheol. , pp. 311, (2010) Best fit, within spin viscosity values calculated by He (2006) and Elborai (2006) for ferrofluids round and substitute to analytic solution Note: At this pressure gradient, MAX spin velocity is not necessarily small. We are kind of pushing the limit of small spin velocities Zero electric field solution of Poiseuille parabolic profile Huang Analytic Solutions V. S. Lemaire Numeric Solutions Agreement achieved for the all voltages considered! (Rounding of critical electric field strength is only within 3%) Note: if we use particle diameter for spin viscosity, Three orders of magnitude less than best fit value. Likely supports ER fluid parcel Ultrasound velocity profile measurements from Prof. Lemaire’s group likely support our finite physical picture spin viscosity theory combined with our new rotating coffee cup polarization model. 2010 Huang,

Some Applications of Phenomenon and Theory Potential applications of the negative electrorheology phenomenon 1. Micro or nano fluidic pumping 2. Electrically responsive smart materials 3. Electrically variable damping devices 4. Clutch or torque transmission devices Applications of theory presented herein 1. Negative electrorheological fluid flow induced by internal micro-particle electrorotation 2. Offers complementary insights towards the ferrofluid spin-up problem in magnetorheology 3. Electrically or magnetically controlled suspensions in bio systems

This work is partially supported by the United States-Israel Binational Science Foundation (BSF) through grant No. 2004081. Hsin-Fu Huang is financially supported by the National Science Council (Taipei, Taiwan) through the Taiwan Merit Scholarships (contract No. TMS-094 -2 -A-029).

References Boissy C. , P. Atten, and J. N. Foulc 1995, Journal of Electrostatics, 35, pp. 13 -20. Brenner H. 1970, Annual Review of Fluid Mechanics, 2, pp. 137 -176. Cebers A. 1980, Mechanics of Liquid and Gas (in Russian), 2, pp. 86 -93. Cebers A. , E. Lemaire, and L. Lobry 2000, Magnetohydrodynamics, 36, pp. 347 -364. Cebers A. , E. Lemaire, and L. Lobry 2002, International Journal of Modern Physics B, 16, pp. 2063 -2069. Condiff D. W. and Dahler J. S. 1964, Physics of Fluids, 7(6), pp. 842 -854. Dahler J. S. and Scriven L. E. 1961, Nature, 192, pp. 36 -37. Dahler J. S. and Scriven L. E. 1963, Proceedings of the Royal Society A, 275, pp. 504 -527. Elborai S. M. 2006, Ferrofluid surface and volume flows in uniform rotating magnetic fields, Ph. D. Dissertation, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA. Haus H. A. and Melcher J. R. 1989, Electromagnetic Fields and Energy, Prentice-Hall, Englewood Cliffs, NJ. He X. 2006, Ferrohydrodynamic flows in uniform and non-uniform rotating magnetic fields , Ph. D. Dissertation, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA. Jackson J. D. 1999, Classical Electrodynamics, 3 rd edn. , John Wiley, New York, NY. Jones T. B. 1984, IEEE Transactions of Industrial Applications, IA-20, pp. 845 -849. Jones T. B. 1995, Electromechanics of Particles, Cambridge University Press, New York, NY. Kaloni P. N. 1992, International Journal of Engineering Science, 30, pp. 1451 -1457. Lemaire E. , Lobry L. , and Pannacci N. 2006, Journal of Electrostatics, 64, pp. 586 -590. Lemaire E. , Lobry L. , and Pannacci N. 2008, Journal of Rheology, 52(3), pp. 769 -783. Lobry L. and Lemaire E. 1999, Journal of Electrostatics, 47, pp. 61 -69. Lukaszewicz G. 1999, Micropolar Fluids: Theory and Applications, Birkhauser, Boston, MA. Melcher J. R. 1981, Continuum Electromechanics, MIT Press, Cambridge, MA. Pannacci N. 2006, Rotation de Quincke dans des Suspensions, Doctoral Thesis, CNRS-Universite de Nice, Sophia Antipolis. Pannacci N. , Lemaire E. , Lobry L. 2007, Rheol. Acta, 46, pp. 899 -904. Peters F. , L. Lobry, and E. Lemaire 2010, Journal of Rheology, 54, pp. 311 -325. Quincke G. 1896, Ann. Phys. Chem. , 59, pp. 417 -486. Rinaldi C. 2002, Continuum modeling of polarizable systems, Ph. D. Dissertation, Department of Chemical Engineering, MIT, Cambridge, MA. Rinaldi C. and M. Zahn 2002, Physics of Fluids, 14(8), pp. 2847 -2870. Rosensweig R. E. 1997, Ferrohydrodynamics, Dover (reprint), Mineola, NY. Shliomis M. I. 1972, Soviet Phys. JEPT, 34, pp. 1291 -1294. Shliomis M. I. 2002, LNP 594, S. Odenbach (ed. ), pp. 85 -111, Springer-Verlag, Berlin Heidelberg. Wu C. W. and H. Conrad 1997, Journal of Rheology, 41, pp. 267 -281. Zaitsev V. M. and M. I. Shliomis 1969, Journal of Applied Mechanics and Technical Physics, 10, pp. 696 -700.