Microeconomics Corso E John Hey What do

Microeconomics Corso E John Hey

What do we know? • The reservation price of a buyer is. . . • . . . the maximum price he or she would pay. • The reservation price of a seller is. . . • . . . the minimum price he or she would accept.

What do we know? • The surplus of a buyer is. . . • . . . the area between the price paid and the demand curve. • The surplus of a seller is. . . • . . . the area between the price received and the supply curve. • An indifference curve is. . . • . . . a set of points about which the individual is indifferent.

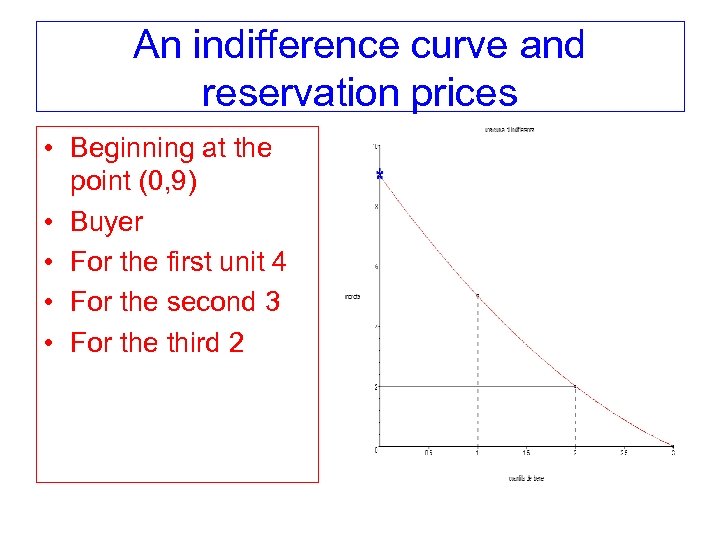An indifference curve and reservation prices • Beginning at the point (0, 9) • Buyer • For the first unit 4 • For the second 3 • For the third 2

Reservation prices and the demand curve • [Beginning at the point (0, 9)] • Buyer • For the first unit 4 • For the second 3 • For the third 2

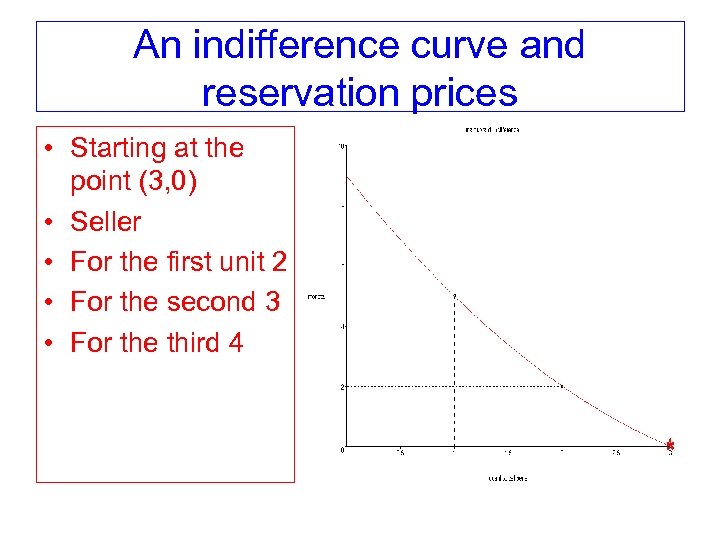An indifference curve and reservation prices • Starting at the point (3, 0) • Seller • For the first unit 2 • For the second 3 • For the third 4

Reservation prices and the supply curve • [Starting at the point (3, 3)] • Seller • For the first unit 2 • For the second 3 • For the third 4

Deduction and inference • If we know the preferences of the individual (the indifference curves or the reservation prices) and the endowment of the individual. . . • . . . we can deduce the demand curve or the supply curve of the individual. . . • If instead we observe the demand supply of the individual. . . • . . . we can infer the preferences of the individual.

Deduction and inference The preferences of the individual (the indifference curves or the reservationprices) and the endowment Whether the individual is a buyer or a seller and either the demand or supply curve of the individual.

A Quiz • I do not like Japanese beer. . . • . . . hence I never buy Japanese beer. • Hence my indifference curves (between money and Japanese beer) are. . . ? • . . . • My reservation prices (as a buyer) for Japanese beer are. . ?

Chapter 4 • In Chapter 3 we have worked with a discrete good – that is, a good that can be traded in integer units. • In Chapter 4 we work with a perfectly divisible good. . which can be traded in any quantities, not only integer units. • We continue to work with a particular kind of preferences – quasi-linear. . . • . . . which imply indifference curves parallel in a vertical direction.

If you like mathematics. . . • m – 60/q = costant is the equation of an indifference curve – the larger the constant, the higher the indifference curve. • pq + m = 3 p + 30 is the equation of the budget line. Here 3 is the endowment of the good and 30 that of money, p is the price of the good, q the quantity consumed and m the amount of money left to spend on other goods. • If we maximise the constant given the budget constraint we obtain the gross demand for the good: • q = √(60/p) • The individual begins with 3 units of the good; hence the net demand is: • q = √(60/p) – 3 • Note: this is positive if p < 60/9 = 6. 66666. . . • is negative if p > 60/9 = 6. 6666. . . • is zero if p = 60/9 = 6. 6666. .

Chapter 4 • Goodbye!