Microeconomics A Anna Kukla-Gryz E-mail akukla wne uw edu

Microeconomics A Anna Kukla-Gryz E-mail: akukla@wne. uw. edu. pl

Requirements for passing the course u Passing the course, two elements: Ø 1 st element: exam (70 % of the total points) Ø 2 nd element: grade from tutorials (30 % of the total points). To pass you need: Ø at least 50 % of the total points from the exam AND Ø at least 50 % of the total points from tutorials

Final test u u The exam will be held on the exam period, The exam – multiple choice test (five answers proposed to each question, only one is correct). The test must be passed with a positive result (at least 50% of the total points). It will be organized only once. Absence at the final test (on the required date) results in failing the course.

Exam Retake u In the retake exam period (in March) there will be only one final test organized, taking the same form as the normal final test. u All participants of the course are allowed to take the retake test, regardless of the result from the first approach. u Taking the retake exam cancels the result obtained from the first approach.

Other rules u All tests are organized according to the rules of "Zero tolerance for cheating". u There are no other possibilities (neither new dates nor rules) for passing the course.

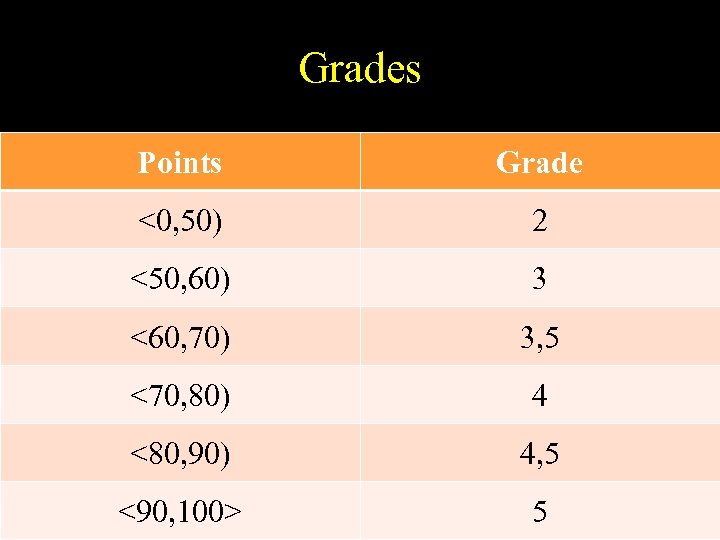Grades Points Grade <0, 50) 2 <50, 60) 3 <60, 70) 3, 5 <70, 80) 4 <80, 90) 4, 5 <90, 100> 5

Readings u Varian H. R. , Intermediate Microeconomics: A Modern Approach, W. W. Norton & Co Ltd. , New York, London, 2006 u Bergstrom T. C. , Varian, H. R. , Workouts in Intermediate Microeconomics, W. W. Norton & Co Ltd. , New York, London, 2006 http: //www. microeconomics. wne. uw. edu. pl/index. php? n=Main. A

Mathematics u u Sydsaeter, K. P. , Hammond, A. , Essential Mathematics for Economic Analysis, Prentice Hall, 2008 Sydsaeter, K. P. , Hammond, A. , Seierstad, A. , Strom. , A. , Further Mathematics for Economic Analysis, Prentice Hall, 2008

Introduction u What are the key themes of microeconomics? u Why study microeconomics? © 2005 Pearson Education, Inc. Chapter 1 11

Themes of Microeconomics u Microeconomics deals with limits – Limited budgets – Limited time – Limited ability to produce u How do we allocate scarce resources? © 2005 Pearson Education, Inc. Chapter 1 12

Themes of Microeconomics u Workers, firms and consumers must make trade-offs – Do I work or go on vacation? – Do I purchase a new car or save my money? – Do we hire more workers or buy new machinery? u How are these trade-offs best made? © 2005 Pearson Education, Inc. Chapter 1 13

Themes of Microeconomics u Prices – Trade-offs are often based on prices faced by consumers and producers – Workers make decisions based on prices for labor – wages – Firms make decisions based on wages and prices for inputs and on prices for the goods they produce © 2005 Pearson Education, Inc. Chapter 1 17

Themes of Microeconomics u Prices – How are prices determined? v. Centrally planned economies – governments control prices v. Market economies – prices determined by interaction of market participants – Markets – collection of buyers and sellers whose interaction determines the prices of goods Chapter 1 © 2005 Pearson Education, Inc. 18

Theories and Models u Economics is concerned with explanation of observed phenomena – Theories are used to explain observed phenomena in terms of a set of basic rules and assumptions: v. Theory of the Firm v. Theory of Consumer Behavior © 2005 Pearson Education, Inc. Chapter 1 19

Budgetary and Other Constraints on Choice Source: Hal R. Varian

Consumption Choice Sets u. A consumption choice set is the collection of all consumption choices available to the consumer. u What constrains consumption choice? – Budgetary, time and other resource limitations.

Budget Constraints u. A consumption bundle containing x 1 units of commodity 1, x 2 units of commodity 2 and so on up to xn units of commodity n is denoted by the vector (x 1, x 2, … , xn). u Commodity prices are p 1, p 2, … , pn.

Budget Constraints u Q: When is a consumption bundle (x 1, … , xn) affordable at given prices p 1, … , p n ?

Budget Constraints u Q: When is a bundle (x 1, … , xn) affordable at prices p 1, … , pn? u A: When p 1 x 1 + … + p n x n £ m where m is the consumer’s (disposable) income.

Budget Constraints u The bundles that are only just affordable form the consumer’s budget constraint. This is the set { (x 1, …, xn) | x 1 ³ 0, …, xn ³ 0 and p 1 x 1 + … + pnxn = m }.

Budget Constraints u The consumer’s budget set is the set of all affordable bundles; B(p 1, … , pn, m) = { (x 1, … , xn) | x 1 ³ 0, … , xn ³ 0 and p 1 x 1 + … + p n x n £ m } u The budget constraint is the upper boundary of the budget set.

x 2 m /p 2 Budget Set and Constraint for Two Commodities Budget constraint is p 1 x 1 + p 2 x 2 = m. m /p 1 x 1

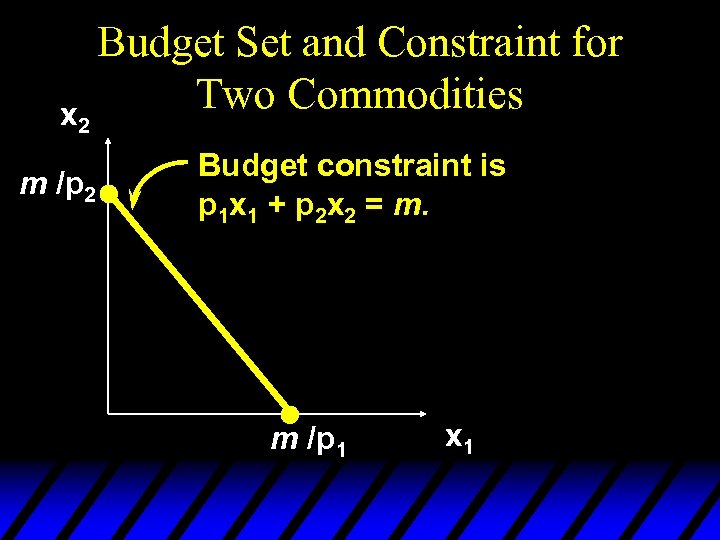x 2 m /p 2 Budget Set and Constraint for Two Commodities Budget constraint is p 1 x 1 + p 2 x 2 = m. m /p 1 x 1

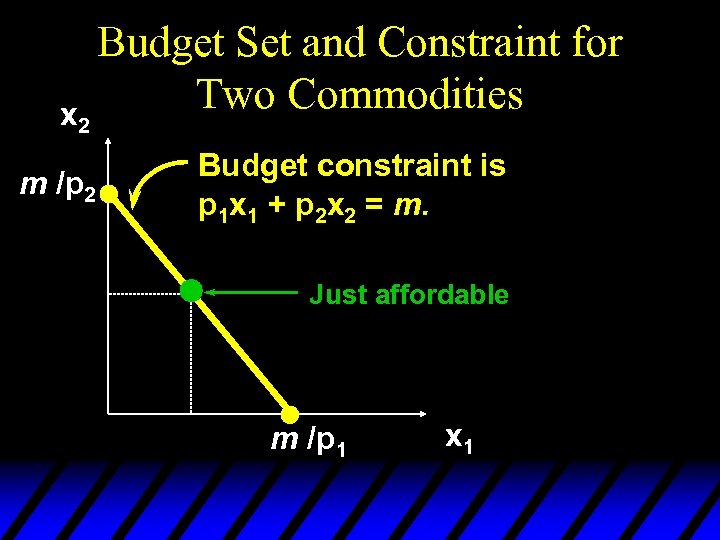x 2 m /p 2 Budget Set and Constraint for Two Commodities Budget constraint is p 1 x 1 + p 2 x 2 = m. Just affordable m /p 1 x 1

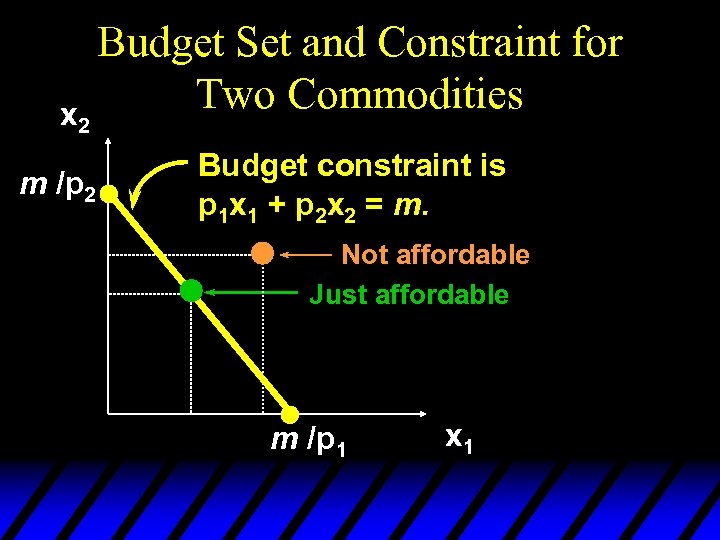x 2 m /p 2 Budget Set and Constraint for Two Commodities Budget constraint is p 1 x 1 + p 2 x 2 = m. Not affordable Just affordable m /p 1 x 1

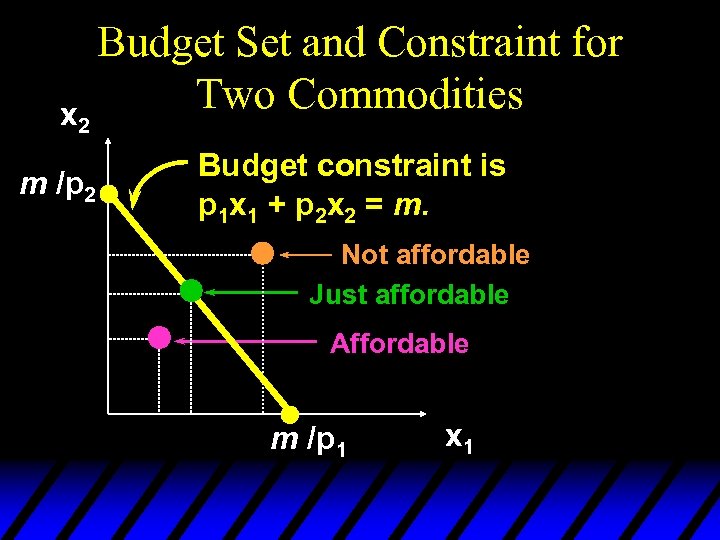x 2 m /p 2 Budget Set and Constraint for Two Commodities Budget constraint is p 1 x 1 + p 2 x 2 = m. Not affordable Just affordable Affordable m /p 1 x 1

x 2 m /p 2 Budget Set and Constraint for Two Commodities Budget constraint is p 1 x 1 + p 2 x 2 = m. the collection of all affordable bundles. Budget Set m /p 1 x 1

x 2 m /p 2 Budget Set and Constraint for Two Commodities p 1 x 1 + p 2 x 2 = m is x 2 = -(p 1/p 2)x 1 + m/p 2 so slope is -p 1/p 2. Budget Set m /p 1 x 1

Budget Constraints u If n = 3 what do the budget constraint and the budget set look like?

Budget Constraint for Three Commodities x 2 m /p 2 p 1 x 1 + p 2 x 2 + p 3 x 3 = m m /p 3 m /p 1 x 3

Budget Set for Three Commodities x 2 m /p 2 { (x 1, x 2, x 3) | x 1 ³ 0, x 2 ³ 0, x 3 ³ 0 and p 1 x 1 + p 2 x 2 + p 3 x 3 £ m} m /p 3 m /p 1 x 3

Budget Constraints u For n = 2 and x 1 on the horizontal axis, the constraint’s slope is -p 1/p 2. What does it mean?

Budget Constraints u For n = 2 and x 1 on the horizontal axis, the constraint’s slope is -p 1/p 2. What does it mean? u Increasing p 1/p 2. x 1 by 1 must reduce x 2 by

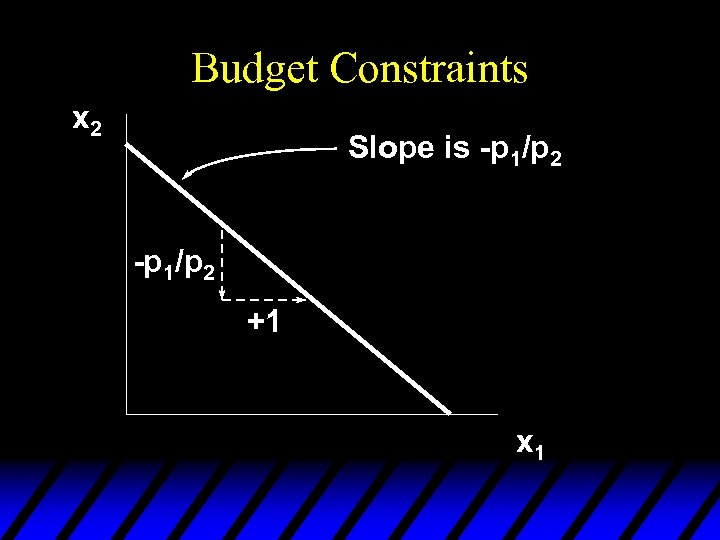Budget Constraints x 2 Slope is -p 1/p 2 +1 x 1

Budget Constraints x 2 Opp. cost of an extra unit of commodity 1 is p 1/p 2 units foregone of commodity 2. -p 1/p 2 +1 x 1

Budget Constraints x 2 Opp. cost of an extra unit of commodity 1 is p 1/p 2 units foregone of commodity 2. And the opp. cost of an extra +1 unit of commodity 2 is -p 2/p 1 units foregone of commodity 1. x 1

Budget Sets & Constraints; Income and Price Changes u The budget constraint and budget set depend upon prices and income. What happens as prices or income change?

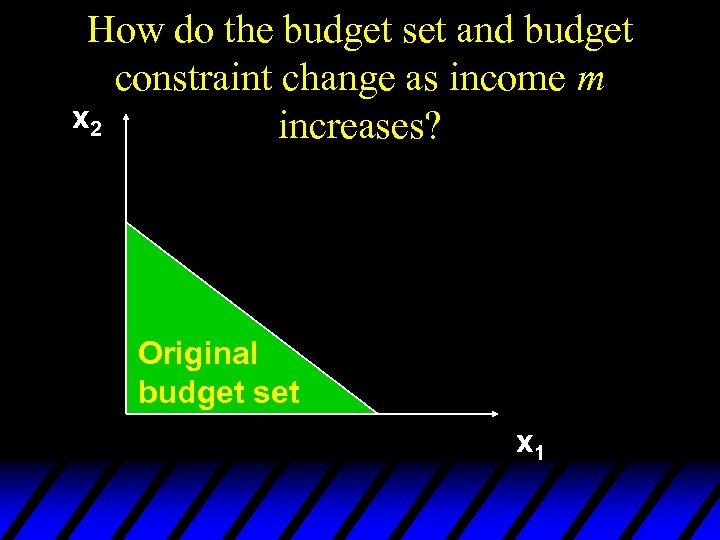How do the budget set and budget constraint change as income m x 2 increases? Original budget set x 1

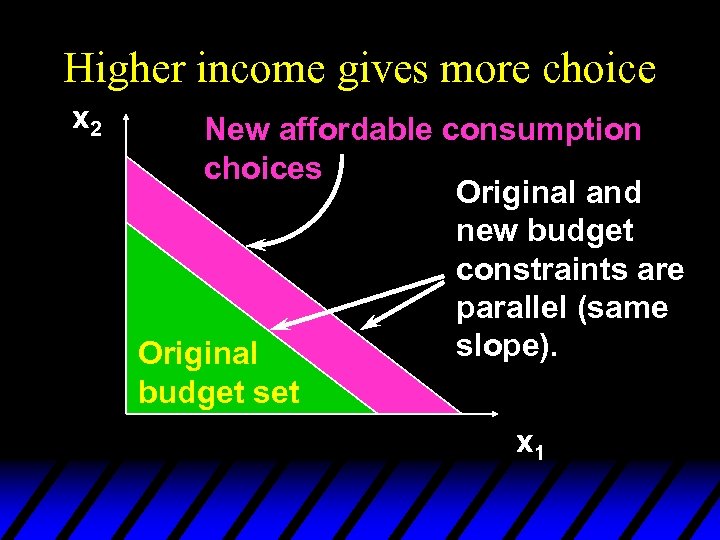Higher income gives more choice x 2 New affordable consumption choices Original and new budget constraints are parallel (same slope). Original budget set x 1

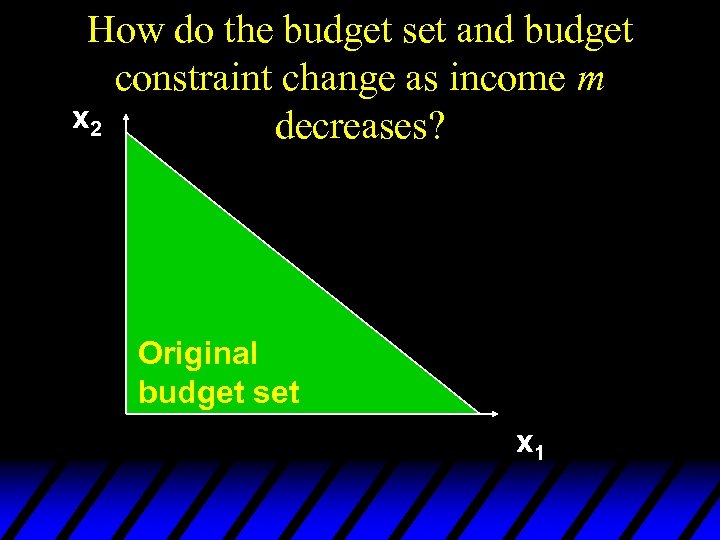How do the budget set and budget constraint change as income m x 2 decreases? Original budget set x 1

How do the budget set and budget constraint change as income m x 2 decreases? Consumption bundles that are no longer affordable. New, smaller budget set Old and new constraints are parallel. x 1

Budget Constraints - Income Changes u Increases in income m shift the constraint outward in a parallel manner, thereby enlarging the budget set and improving choice.

Budget Constraints - Income Changes u Increases in income m shift the constraint outward in a parallel manner, thereby enlarging the budget set and improving choice. u Decreases in income m shift the constraint inward in a parallel manner, thereby shrinking the budget set and reducing choice.

Budget Constraints - Income Changes u No original choice is lost and new choices are added when income increases, so higher income cannot make a consumer worse off. u An income decrease may (typically will) make the consumer worse off.

Budget Constraints - Price Changes u What happens if just one price decreases? u Suppose p 1 decreases.

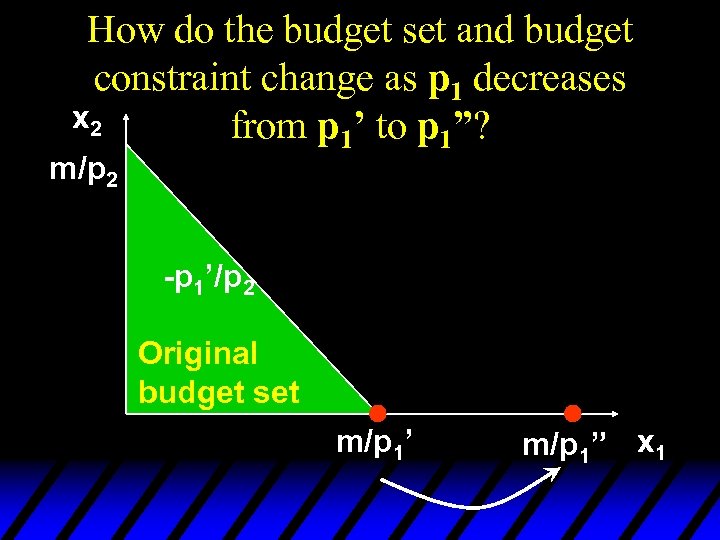How do the budget set and budget constraint change as p 1 decreases x 2 from p 1’ to p 1”? m/p 2 -p 1’/p 2 Original budget set m/p 1’ m/p 1” x 1

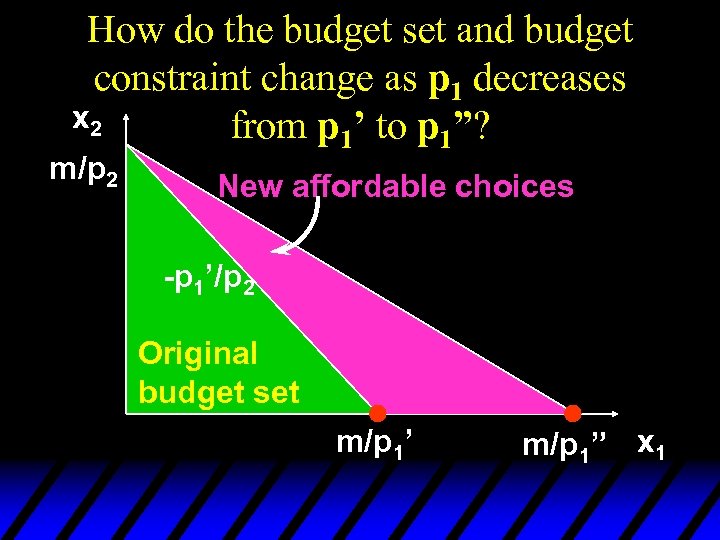How do the budget set and budget constraint change as p 1 decreases x 2 from p 1’ to p 1”? m/p 2 New affordable choices -p 1’/p 2 Original budget set m/p 1’ m/p 1” x 1

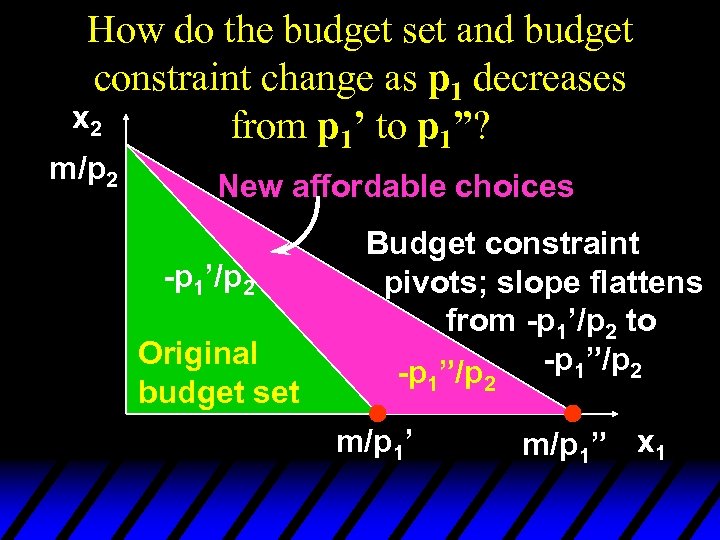How do the budget set and budget constraint change as p 1 decreases x 2 from p 1’ to p 1”? m/p 2 New affordable choices -p 1’/p 2 Original budget set Budget constraint pivots; slope flattens from -p 1’/p 2 to -p 1”/p 2 -p ”/p 1 m/p 1’ 2 m/p 1” x 1

Budget Constraints - Price Changes u Reducing the price of one commodity pivots the constraint outward. No old choice is lost and new choices are added, so reducing one price cannot make the consumer worse off.

Budget Constraints - Price Changes u Similarly, increasing one price pivots the constraint inwards, reduces choice and may (typically will) make the consumer worse off.

Uniform Ad Valorem Sales Taxes u An ad valorem sales tax levied at a rate of 5% increases all prices by 5%, from p to (1+0× 05)p = 1× 05 p. u An ad valorem sales tax levied at a rate of t increases all prices by tp from p to (1+t)p. u A uniform sales tax is applied uniformly to all commodities.

Uniform Ad Valorem Sales Taxes u. A uniform sales tax levied at rate t changes the constraint from p 1 x 1 + p 2 x 2 = m to (1+t)p 1 x 1 + (1+t)p 2 x 2 = m

Uniform Ad Valorem Sales Taxes u. A uniform sales tax levied at rate t changes the constraint from p 1 x 1 + p 2 x 2 = m to (1+t)p 1 x 1 + (1+t)p 2 x 2 = m i. e. p 1 x 1 + p 2 x 2 = m/(1+t).

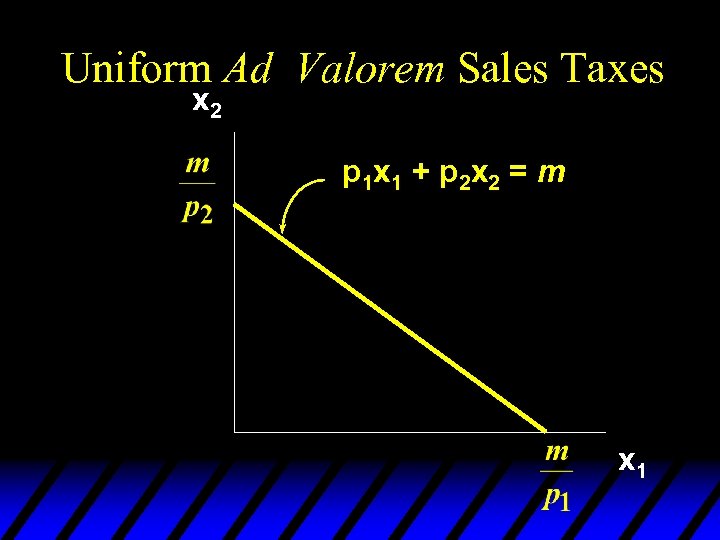Uniform Ad Valorem Sales Taxes x 2 p 1 x 1 + p 2 x 2 = m x 1

Uniform Ad Valorem Sales Taxes x 2 p 1 x 1 + p 2 x 2 = m/(1+t) x 1

Uniform Ad Valorem Sales Taxes x 2 Equivalent income loss is x 1

Uniform Ad Valorem Sales Taxes x 2 A uniform ad valorem sales tax levied at rate t is equivalent to an income tax levied at rate x 1

The Food Stamp Program u Food stamps are coupons that can be legally exchanged only for food. u How does a commodity-specific gift such as a food stamp alter a family’s budget constraint?

The Food Stamp Program u Suppose m = $100, p. F = $1 and the price of “other goods” is p. G = $1. u The budget constraint is then F + G =100.

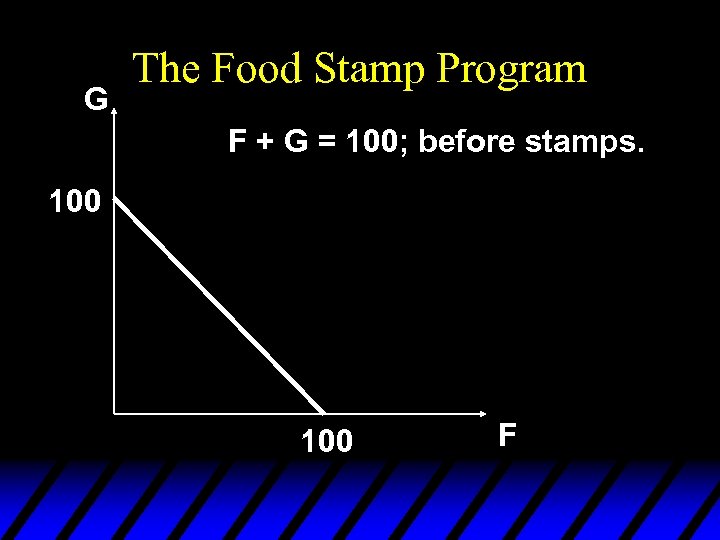G The Food Stamp Program F + G = 100; before stamps. 100 F

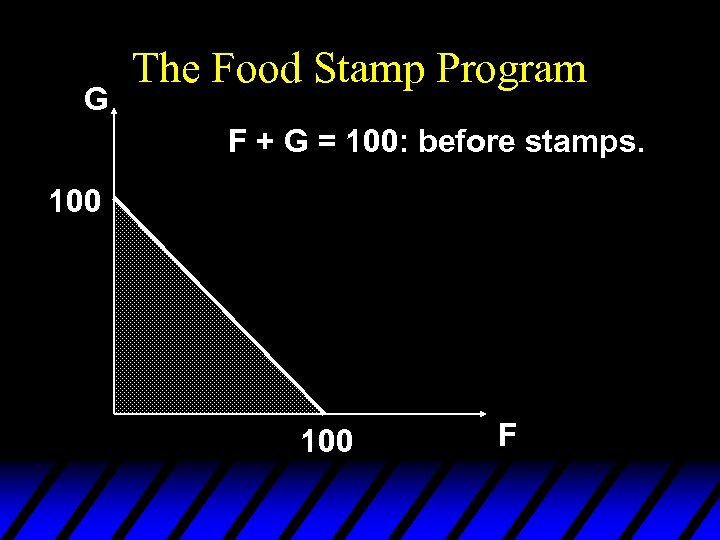G The Food Stamp Program F + G = 100: before stamps. 100 F

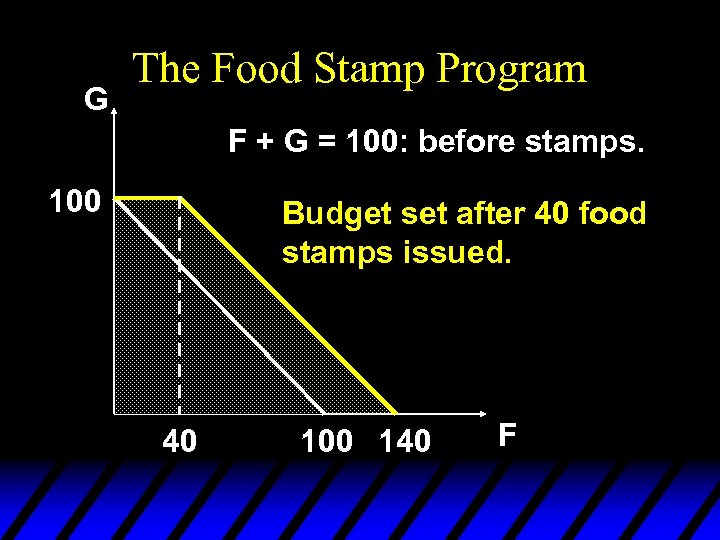G The Food Stamp Program F + G = 100: before stamps. 100 Budget set after 40 food stamps issued. 40 100 140 F

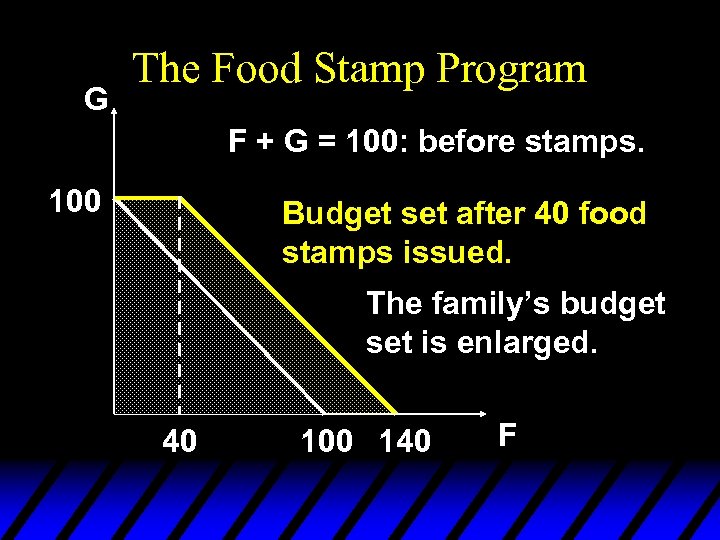G The Food Stamp Program F + G = 100: before stamps. 100 Budget set after 40 food stamps issued. The family’s budget set is enlarged. 40 100 140 F

The Food Stamp Program u What if food stamps can be traded on a black market for $0. 50 each?

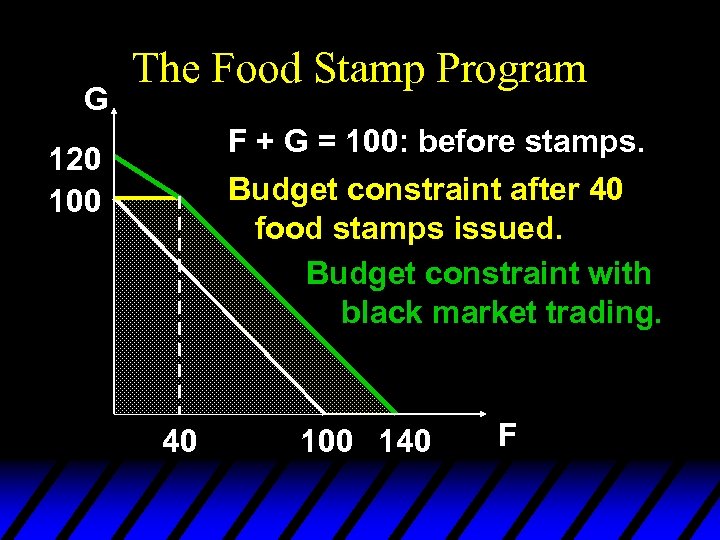G The Food Stamp Program F + G = 100: before stamps. Budget constraint after 40 food stamps issued. Budget constraint with black market trading. 120 100 40 100 140 F

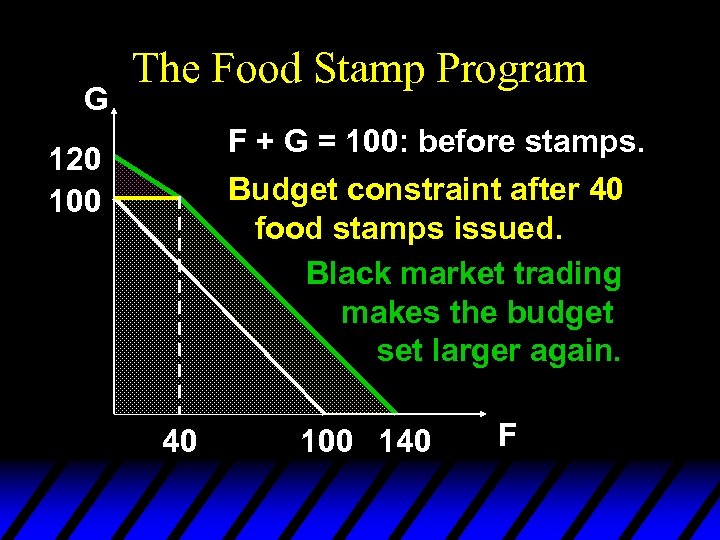G The Food Stamp Program F + G = 100: before stamps. Budget constraint after 40 food stamps issued. Black market trading makes the budget set larger again. 120 100 40 100 140 F