Межпредметные связи математики и предметов естественнонаучного цикла Кондрашова

Межпредметные связи математики и предметов естественнонаучного цикла Кондрашова Елена Анатольевна МОУ «СОШ № 11» г. о. Электросталь

Предметы естественноматематического цикла дают учащимся знания: о живой и неживой природе o о материальном единстве мира o о природных ресурсах и их использовании в хозяйственной деятельности человека o

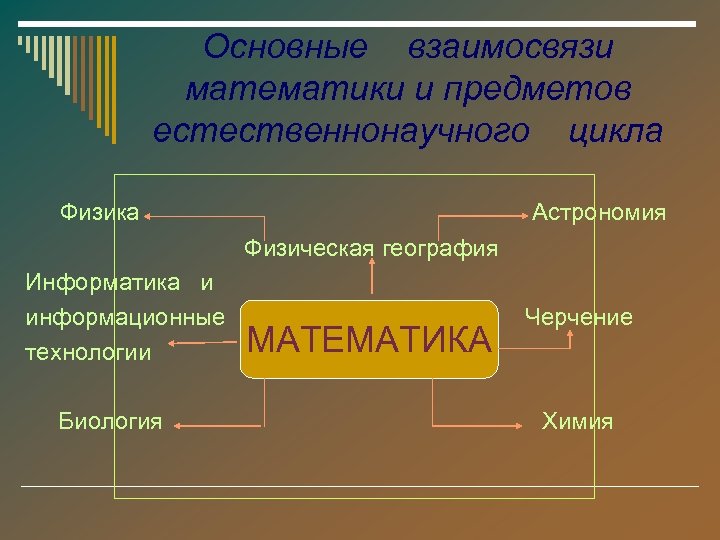Основные взаимосвязи математики и предметов естественнонаучного цикла Физика Астрономия Физическая география Информатика и информационные технологии Биология МАТЕМАТИКА Черчение Химия

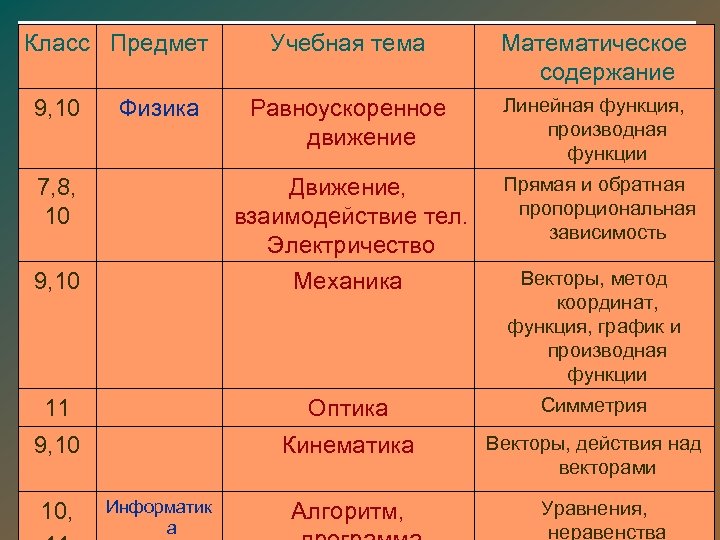Класс Предмет Учебная тема Математическое содержание Равноускоренное движение Линейная функция, производная функции Прямая и обратная пропорциональная зависимость 9, 10 Движение, взаимодействие тел. Электричество Механика 11 Оптика Симметрия 9, 10 Кинематика Векторы, действия над векторами 9, 10 Физика 7, 8, 10 10, Информатик а Алгоритм, Векторы, метод координат, функция, график и производная функции Уравнения, неравенства

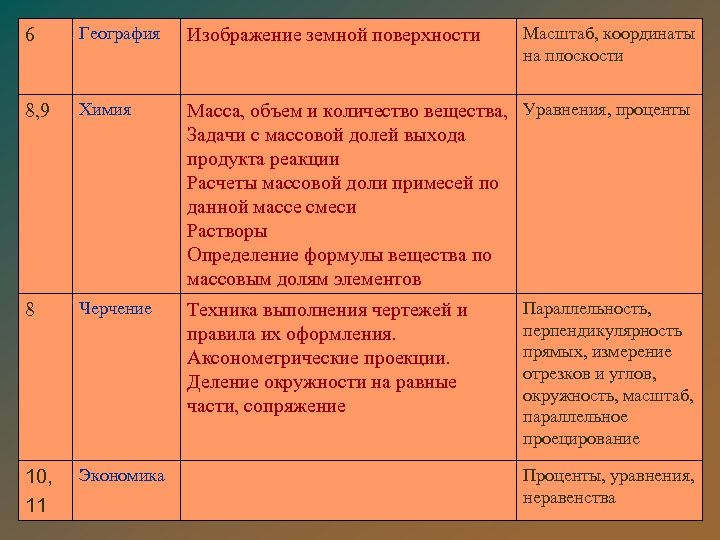6 География Изображение земной поверхности Масштаб, координаты на плоскости 8, 9 Химия Масса, объем и количество вещества, Уравнения, проценты Задачи с массовой долей выхода продукта реакции Расчеты массовой доли примесей по данной массе смеси Растворы Определение формулы вещества по массовым долям элементов 8 Черчение Техника выполнения чертежей и правила их оформления. Аксонометрические проекции. Деление окружности на равные части, сопряжение 10, 11 Экономика Параллельность, перпендикулярность прямых, измерение отрезков и углов, окружность, масштаб, параллельное проецирование Проценты, уравнения, неравенства

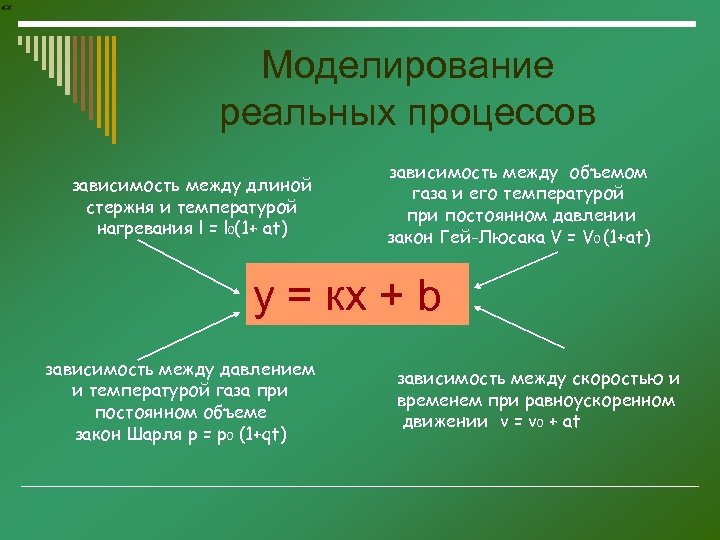Моделирование реальных процессов зависимость между длиной стержня и температурой нагревания l = l 0(1+ at) зависимость между объемом газа и его температурой при постоянном давлении закон Гей-Люсака V = V 0 (1+at) у = кх + b зависимость между давлением и температурой газа при постоянном объеме закон Шарля p = p 0 (1+qt) зависимость между скоростью и временем при равноускоренном движении v = v 0 + at

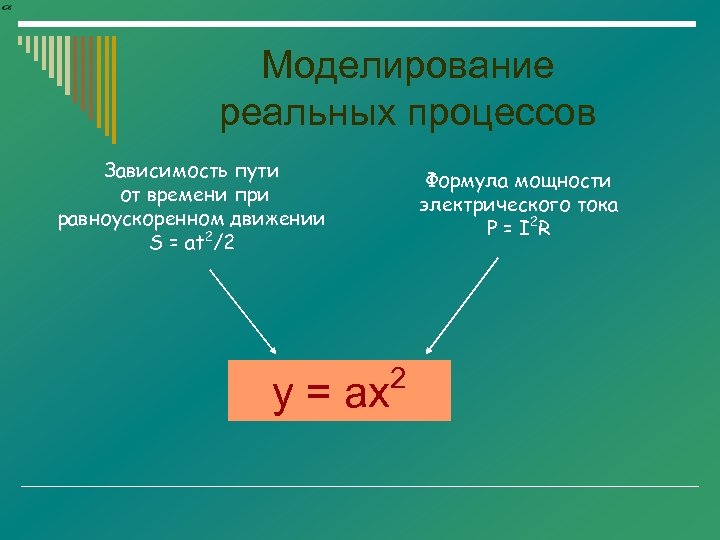Моделирование реальных процессов Зависимость пути от времени при равноускоренном движении S = at 2/2 у = ах Формула мощности электрического тока P = I 2 R 2

Моделирование как метод познания включает в себя: • построение, конструирование модели; • исследование модели(экспериментальное или мысленное); • анализ полученных данных и перенос их на подлинный объект изучения. Три этапа решения прикладных задач: 1. построение модели (перевод условия задачи с обыденного на математический язык) 2. работа с моделью (решение уравнения, неравенства и т. д. ) 3. ответ на вопрос задачи

Система задач с физическим содержанием при изучении темы «Векторы» в 8 -9 классах на примере раздела «Динамика» Векторные умения и навыки наглядно демонстрируют модельный характер этого материала. Вводя понятие «вектора» можно предложить учащимся следующие задачи-вопросы, знакомые из повседневной практики: Задача 1. Может ли автомобиль двигаться по горизонтальному шоссе с выключенным двигателем? Задача 2. На горизонтальном участке пути маневровый тепловоз толкнул вагон. Какие силы действуют на вагон во время толчка и при движении после него?

Графические упражнения позволяют учащимся перевести физическую ситуацию на геометрический язык и получать информацию о физических явлениях с помощью геометрической модели векторного пространства. Задача 4. На нити подвешен груз (рис. 2). Изобразите графически силы, действующие на груз (масштаб: 1 см – 5 Н). Задача 5. Изобразите графически силы, действующие на доску АВ. Обозначьте буквами точки приложения этих сил (рис. 4). (рис. 2) (рис. 4)

q. Для усвоения зависимости векторной величины не только от числового значения, но и от направления следует предложить задачи такого типа: Задача 6. Изобразить в данном масштабе силу, модуль которой равен 4 Н. Сколько решений имеет задача? Задача 7. Изобразить графически силу, направленную вертикально вниз, модуль которой равен 50 Н (масштаб: 1 клетка – 10 Н). Для подготовки изучения общего случая сложения и вычитания векторов можно использовать задачи на нахождение равнодейтвующей сил, действующих по одной прямой. Задача 10. Чему равна равнодействующая двух сил, прложенных к телу в т. А (рис. 5) 2 Н А 4 Н Задача 16. На тело вдоль одной прямой действуют две силы, модули которых 20 Н и 30 Н. Изобразите эти силы графически для случаев, когда их равнодействующая равна 50 Н и 10 Н.

Правила треугольника и параллелограмма, можно продемонстрировать в задачах следующего типа: F тяги Задача 17. Как направлено ускорение, с которым летит вертолет Бабы Яги, если сила тяги его винта направлена, как показано на рис. 8. mg

После изучения равенства векторов и понятия нулевого вектора можно решить задачи следующего содержания: q Задача 19. Объясните, действия каких сил компенсируются в следующих случаях: а) подводная лодка покоится в толще воды; б) подводная лодка лежит на морском дне. q Задача 22. Двое мальчиков тянут за динамометр в противоположные стороны с силами по 100 Н каждый. Каково показание динамометра? q Задача 23. На тело горизонтально действует сила 3 Н. Какую силу надо приложить к телу, чтобы тело не двигалось?

При изучении параграфа «Умножение вектора на число» свойство получать коллинеарный вектор можно проиллюстрировать задачами на закон Гука и II закон Ньютона. o Задача 25. Сила в 60 Н сообщила телу ускорение 0, 8 м/с2. Какая сила сообщит этому телу ускорение 2 м/с2. o Задача 27. Под действием силы 4 Н пружина удлинилась на 5 мм. Определить вес груза, под действием которого эта пружина удлинится на 16 мм.

После изучения всей темы «Векторы» можно периодически давать учащимся задачи на повторение пройденного, включая их в самостоятельные, домашние работы, чтобы углубить и упрочить знания о свойствах векторов. o Задача 28. По гладкой наклонной поверхности под углом 300 движется тело, на которое действует сила тяжести 17 Н. Какие ещё силы действуют на тело? Чему равна равнодействующая приложенных сил? Силой трения пренебречь. o Задача 29. Автодрезина ведет равноускоренно две платформы. Сила тяги 1078 к. Н. Масса первой платформы 12 т, второй – 8 т. С какой силой упругости натянута сцепка между платформами? o Задача 34. Лодку равномерно тянут к берегу 2 -мя канатами, расположенными под углом 900. К канатам приложена сила 120 Н к каждому. Какова сила сопротивления воды?

Задачи на смеси и сплавы + =

Пример: Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200 г сплава, содержащего 30% меди? М С 15% хг М + 65% С М = С 30% (200 - х) г 200 г Составим уравнение: 0, 15 х + 0, 65(200 - х) = 0, 3 • 200

II способ. Можно обозначить х г и у г массу первого и второго сплава соответственно. М С 15% М + 65% х г С М = С 30% у г 200 г х + у = 200 0, 15 х +0, 65 у = 0, 3*200 х = 140 у = 60 Ответ: 140 г, 60 г.

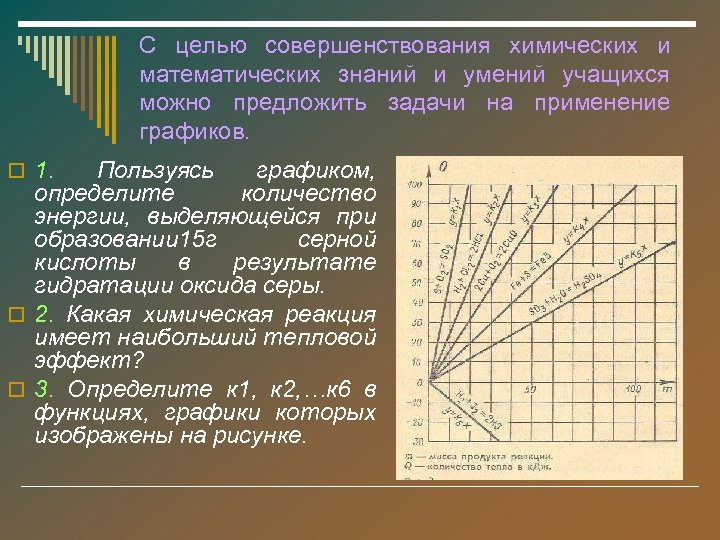С целью совершенствования химических и математических знаний и умений учащихся можно предложить задачи на применение графиков. o 1. Пользуясь графиком, определите количество энергии, выделяющейся при образовании 15 г серной кислоты в результате гидратации оксида серы. o 2. Какая химическая реакция имеет наибольший тепловой эффект? o 3. Определите к 1, к 2, …к 6 в функциях, графики которых изображены на рисунке.

Можно предложить задачи межпредметного характера в ходе изучения других математических тем. Тема: “Многогранники”. 1. 10 -местная палатка представляет собой параллелепипед длиной 5, 2 м, шириной 3, 6 м и высотой 2, 5 м с двускатной крышей, приподнятой на 80 см. Определить объем палатки и количество палаточного материала, необходимого для ее изготовления 2. Кристалл кварца состоит из правильной 6–угольной призмы с боковым ребром 6, 2 см и стороны основания 1, 7 см и двух правильных 6–угольных пирамид с боковым ребром 2, 5 см. Найти объем кристалла. o Тема: “Тела вращения”. 1. В цилиндрический сосуд, наполненный водой до половины, опущен шар диаметром 4 см. Высота сосуда равна 8 см, радиус основания – 2 см. Достигнет ли уровень воды краев сосуда? 2. Земля приблизительно является шаром с радиусом 4, 371 км. Определить длину экватора Земли и длину параллели, проходящих через г. Москву и г. Омск. o Тема: “Векторы. Метод координат в пространстве”. 1. Вычислить работу, производимую силой F {3; – 2; – 5}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А (2; – 3; 5) в положение В (3; – 2; – 1). 2. Цель ограничена точками А (1; 2; – 3), В (0; 4; 2), С (1; – 3; 1). Определить количество снарядов, необходимое для полного разрушения цели, если известно, что для полного разрушения 1 ед 2 площади цели, необходимо 3 снаряда. o Тема: “Векторы. Метод координатной плоскости”. 1. Найти величину силы, которая совершила работу 150 Дж по перемещению из точки К (– 2; 3) в точку М (4; – 5). Сила направлена вдоль линии движения. 2. Команда спортсменов-парашютистов получила задачу на приземление в районе, ограниченном точками: А (5; 4), В (9; 6), С (6; 7). Какова площадь района приземления? o

Тема: “Соотношения между сторонами и углами треугольника”. 1. Обороняемый участок местности по форме является практически ромбом со стороной 2, 3 км и углом равным 1420. Вершина тупого угла направлена в сторону противника (рис. 16). Определить площадь обороняемого участка в гектарах, его ширину по фронту и максимальную глубину. Тема: “Уравнения окружности и прямой”. 1. Одна группа туристов движется по прямой дороге из пункта А (3; 2) в пункт В (8; 6). Другая группа движется по прямой из пункта С (3; 8) в пункт D (– 3; 2). Определить, где необходимо расположить контрольный пункт, чтобы можно было зафиксировать время прохождения этапа маршрута сразу двум группам. 2. Зона обитания двух видов лягушек определяется линиями: x 2+y 2– 2 x– 6 y+6=0, x 2+y 2– 6 x– 10 y+30=0. Показать на чертеже эти участки, а также найти площадь пространства, где одновременно обитают лягушки обоих видов. o Тема: “Уравнение первой и второй степени”. 1. Вертолет пролетел некоторое расстояние по ветру за 1 ч. 15 мин, сбросил груз и при том же самом режиме работы двигателей пролетел это же расстояние обратно (против ветра) за 1 ч. 45 мин. Определить скорость вертолета в спокойной атмосфере, если скорость ветра равна 20 км/ч. 2. В 2 л. водного раствора , содержащего 60% кислоты, добавили 4 л. чистой воды. Определите процентное содержание в новом растворе. 3. В шахту, предназначавшуюся противником для установки баллистической ракеты, бросили без начальной скорости груз, звук от удара которого о дно шахты был услышан через 5 секунд. Определить глубину шахты. 4. Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20% -й раствор кислоты? 5. Имеется чай двух сортов- по 80 р. и 120 р. за один кг. Смешали 300 г. первого и 200 г. второго сорта. Определите цену 100 г. полученной смеси. Тема: “Функции и их графики”. 1. Траектория движения центра масс снаряда приближенно определяется формулой y=0, 04 x– 0, 000008 x 2, где x, y выражаются в м, и начало координат (0; 0) – точка вылета снаряда из канала ствола орудия. Определить максимальную дальность полетов снарядов и наибольшую траекторию полета. o

Тема: “Прогрессии”. 1. Парашютист, покинув самолет, и до раскрытия парашюта, проходит в первую секунду 4, 9 м, а в каждую следующую секунду на 9, 8 м больше, чем в предыдущую. Какое расстояние будет пройдено десантником за 5 секунд. 2. Музыкальная октава делится на 12 равных интервалов – полутонов. Частота каждого последующего звука приблизительно в 1, 059 раза больше частоты предыдущего. Во сколько раз нота соль выше ноты до той же октавы. o Тема: “Производная и ее приложения”. 1. Из пункта А, находящегося в лесу в 5 км от прямолинейной дороги, группе туристов нужно попасть в пункт В, расположенный на этой дороге в 13 км от пункта А. По дороге группа может двигаться с максимальной скоростью 5 км/ч, а по лесной – с максимальной скоростью – 3 км/ч. За какое минимальное время группа сможет добраться из пункта А в пункт В? 2. Доказать, что из всех прямоугольных треугольников, вписанных в данный круг, наибольшую площадь имеет равнобедренный треугольник. 3. Дождевая капля падает под действием силы тяжести, равномерно испаряясь так, что ее масса изменяется по закону m(t) = 1–t(m – в г; t – в с). Через сколько времени после начала падения кинетическая энергия капли будет наибольшей? 4. Источник тока с электродвижущей силой Е = 220 В и внутренним сопротивлением r = 50 Ом подключен к прибору с сопротивлением R. Чему должно быть равно сопротивление R потребителя, чтобы потребляемая им мощность была наибольшей? 5. На автомобиле КРАЗ имеется два топливных бака цилиндрической формы емкостью 200 литров каждый. При каких размерах бака на его изготовление потребуется наименьшее количество металла? o Тема: “Интеграл и его приложения”. 1. Вычислить работу, которую надо произвести, чтобы выкачать воду из резервуара конической формы с вершиной, обращенной книзу. Резервуар наполнен доверху водой. Радиус основания конуса равен 1 м, высота конуса 2 м. 2. Для сжатия пружины на 0, 02 м необходимо совершить работу 16 Дж. На какую длину можно сжать пружину, совершив работу 100 Дж?

Задания для обучения и развития учащихся» , ориентированное на развитие мышления и творческих способностей

Интегрированный урок по теме «Решение рациональных неравенств и их систем» в 9 классе Задание 2: Решите неравенства. С помощью найденных ответов и данной таблицы узнайте, растворы каких веществ находятся в колбах. А (х – 4)(х + 4) + х ≥ х2 – 56 [ -40; + ∞) Б – х2 + 15 х – 14 ≥ 0 [1; 14] В х/3 + (2 x-1)/5 > 2 х – 1/15 (–∞ ; – 2/19 ) Г (6+4 х2)/(х2 -5 х-6) ≤ 0 (– 1; 6 ) Химическая формула Na. Cl H 2 O Числовой код ( – 1; 6 ) [1; 14] Na. OH H 2 SO 4 [ -40; + ∞) (–∞; – 2/19 ) Задание 3: 1) Добавьте в колбы лакмус и объясните изменение цвета раствора.

Проблема осуществление межпредметных связей в процессе обучения требует целенаправленного руководства Категория педагогических Факторы, влияющие на недостаточное работников применение межпредметных связей Молодые специалисты Не имеют опыта и умений применения знаний по родственным своей профессии предметам Учителя с опытом работы Недостаточно владеют методиками от 1 до 3 лет планирования и реализации межпредметных связей на уроках и во внеклассной деятельности Учителя со стажем работы Уже не имеют, как правило, достаточных знаний свыше 15 лет по родственным предметам, нуждаются в усвоении новых трактовок общепредметных понятий, особенностей новых учебных программ по смежным предметам, необходимых для реализации межпредметных связей