Межатомные взаимодействия в конденсированных средах Уравнения движения

Межатомные взаимодействия в конденсированных средах

Уравнения движения классических частиц с потенциальным взаимодействием), . . . , 2, 1( ), . . . , , (21 Ni r rrr. U Fam i N iii Движение системы классических частиц (материальных точек), взаимодействие которых характеризуется потенциальной энергией, описывается системой уравнений II закона Ньютона

Классический потенциал и сила взаимодействия), . . . , , (21 Nrrr. U ), . . . , , ( 21 21 Ni i N irrr. U r rrr. U F Потенциальная энергия системы N атомов Сила, действующая на i- й атом Взаимодействие атомов носит квантовый характер и осуществляется через электроны. Имеет ли обоснование понятие межатомного потенциала?

Но атомы – квантовые объекты ! Строго говоря, взаимодействие атомов носит квантовый характер и осуществляется через электроны. Можно ли описывать их взаимодействие классическим межатомным потенциалом, а движение – классическими уравнениями движения ? В этой лекции ниже дается положительный ответ на первую часть вопроса. Ответ на вторую часть вопроса – в лекции об основах МД.

Уравнение Шредингера для N атомов), (r. REr. RHii ), (r. Ri полная волновая функция системы i. R r ii i ijji ji ii i r. R e. Z rr e RR e. ZZ m p M P H ||||2 1 2 ˆ 2 ˆ22222 радиусы-векторы ядер системы радиусы-векторы электронов оператор Гамильтона системы

Адиабатическое приближение (Борн, Оппенгеймер, 1923)Mme )(); (), ( iii RRrr. R )( i. R — ВФ ядер ); (i. Rr — ВФ электронов )(); ( ||||21 2 ˆ 2 22 22 ii ii i ij ji ji i i RRr. E RRr r. R e. Z rr e RR e. ZZ mp MP Не содержит операторов, воздействующих на координа — ты ядер R i Соответствует взаимодействию ядер непосредственно через кулоновское поле и через электронную подсистему

Адиабатическое приближение продолжение ); ()(); ( iiiel Rr. RURr. H )()(iin. RERH i ij ji ji el r. R e. Z rr e RR e. ZZ mp H ||||21 2 2 22 2 )( 2 2 i ii i n. RU M P H )(); ()( 2 ˆ 2 iiiii i i RRr. ERRr. RU MP системы энергии нойпотенциаль смысл имеет )(i. RU

Парные потенциалы iiijlk kji ij ji i inrrr. Ur. Urrr. U. . . ), , ()(), . . . , , (32121 U 1 – одночастичный член (энергия частиц во внешнем поле или обусловленная граничными условиями (давлением стенок контейнера)) U 2 – двухчастичный (парный) член; взаимодействие каждой пары атомов определяется только их расстоянием друг от друга и не зависит от присутствия других атомов U 3 – трехчастичный член, учитывающий влияние третьего атома на взаимодействие двух атомов При отсутствии внешнего поля и пренебрежении трех- и многочастичными взаимодействиями: ij ji iij jinrrrrr. U 11 21)( 2 1 ), (), . . . , , (

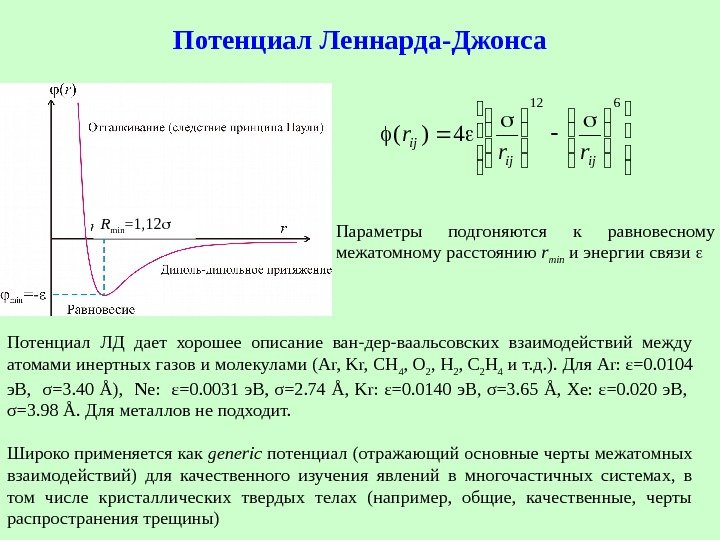
Потенциал Леннарда-Джонса 612 4)( ijij ij rr r Потенциал ЛД дает хорошее описание ван-дер-ваальсовских взаимодействий между атомами инертных газов и молекулами (Ar, Kr, CH 4 , O 2 , H 2 , C 2 H 4 и т. д. ). Для Ar: ε=0. 0104 э. В, σ=3. 40 Å), Ne: ε=0. 0031 э. В, σ=2. 74 Å, Kr: ε=0. 0140 э. В, σ=3. 65 Å, Xe: ε=0. 020 э. В, σ=3. 98 Å. Для металлов не подходит. Широко применяется как generic потенциал (отражающий основные черты межатомных взаимодействий) для качественного изучения явлений в многочастичных системах, в том числе кристаллических твердых телах (например, общие, качественные, черты распространения трещины) Параметры подгоняются к равновесному межатомному расстоянию r min и энергии связи R min =1,

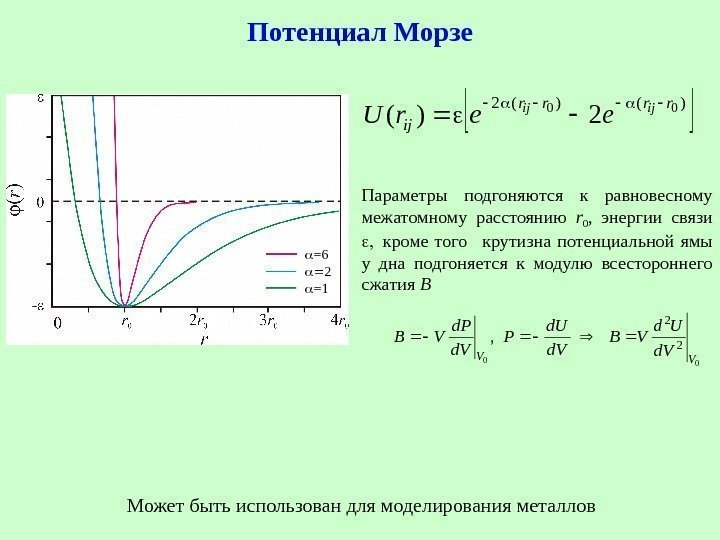
Потенциал Морзе )()(200 2)( rrrr ij ijij eer. U Может быть использован для моделирования металлов Параметры подгоняются к равновесному межатомному расстоянию r 0 , энергии связи кроме того крутизна потенциальной ямы у дна подгоняется к модулю всестороннего сжатия B 00 2 2 , VVd. V Ud VB d. V d. U P d. V d. P VB = 6 2 =

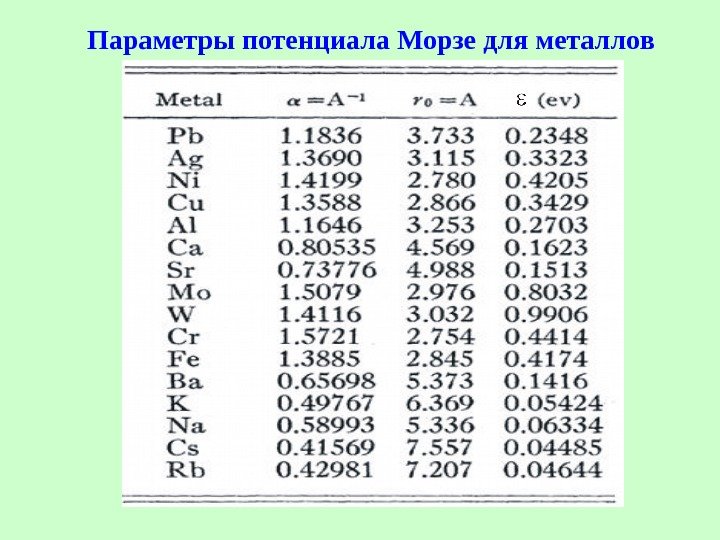
Параметры потенциала Морзе для металлов

Расчет силы для парных потенциалов |)(| 2 1 ), . . . , , (1 )(121 ji ij i. N ijj ji i. Niirrrr r rrr. UF ij ji ij z i ij y i ij xji iji z i y i x dr rrd z r e y r e x r err z e y e x e |)(| ij ij ij ji ijij ij z ij ij y ij ij xf dr rrd r rr dr rrd r z e r y e r x e |)(| Для потенциала ЛД ijijij ji i ijijij ji rr rr F rrdr rrd 6 8 6 7 6 13 12 21 )( 24, 6124 |)(|

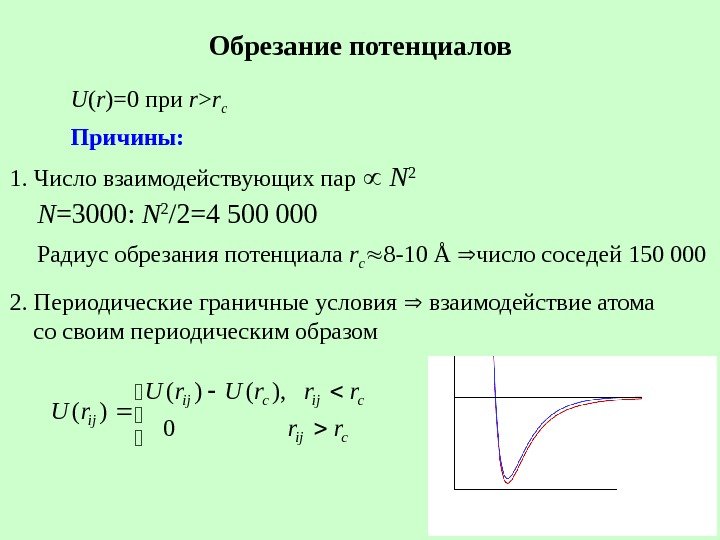
Обрезание потенциалов 1. Число взаимодействующих пар N 2 N =3000: N 2 /2=4 500 000 Радиус обрезания потенциала r c 8 -10 Å число соседей 150 000 U ( r )=0 при r > r c Причины: 2. Периодические граничные условия взаимодействие атома со своим периодическим образом cijcij ij rr rrr. U 0 ), ()( )(

Обрезание потенциалов. Простейший способ cijcij ij rr rrr. U 0 ), ()( )( «Приподнять» функцию на величину – U ( r с ), задав значение радиуса обрезания r с. При этом функция в точке обрезания будет непрерывной, но ее производная испытывает скачок, что приводит к скачкообразным изменениям сил.

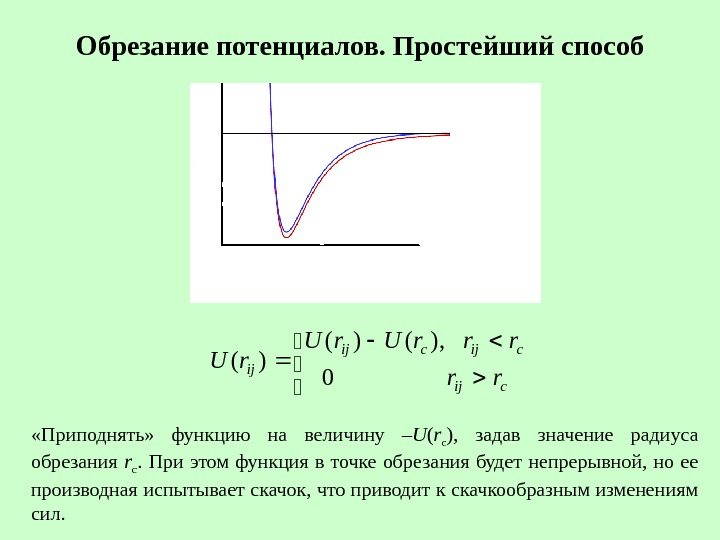
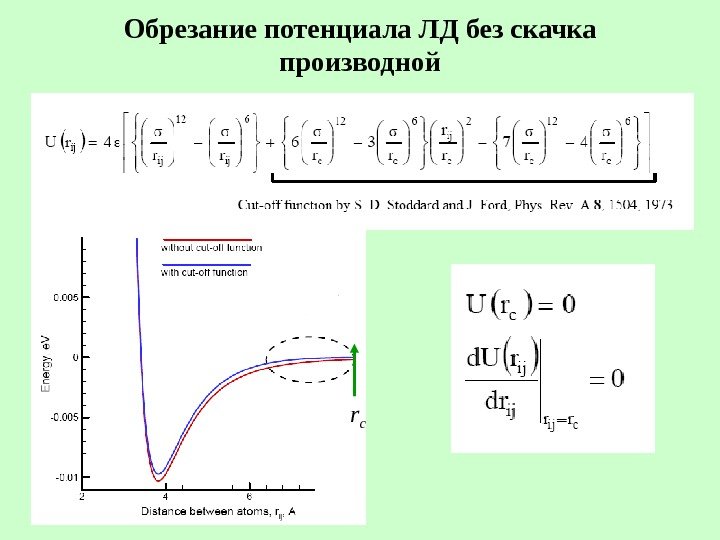
Обрезание потенциала ЛД без скачка производной r c

Недостатки парных потенциалов 1. Не учитывают насыщение связей: энергия на одну связь в объеме меньше, чем на поверхности. 2. Не учитывают зависимость силы связи от направления 3. Дают завышенную энергию образования вакансий 4. Неправильно оценивают упругие константы (выполняется соотношение Коши: ); в действительности: 4412 cc свf. E)35, 025, 0(против 4412/cc 1, 5 для Cu ; 1, 9 для Ag и 3, 7 для Au

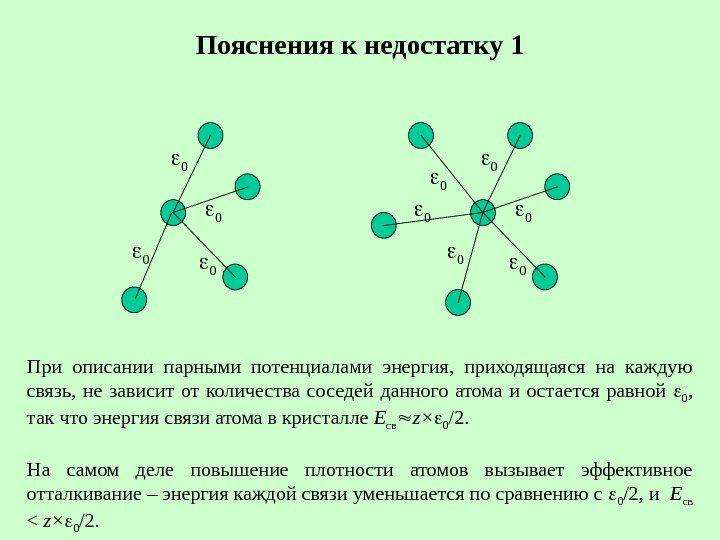
Пояснения к недостатку 1 При описании парными потенциалами энергия, приходящаяся на каждую связь, не зависит от количества соседей данного атома и остается равной 0 , так что энергия связи атома в кристалле E св z× 0 /2. На самом деле повышение плотности атомов вызывает эффективное отталкивание – энергия каждой связи уменьшается по сравнению с 0 /2 , и E св < z× 0 /2.

Тензор упругих постоянных кристаллов: основные формулы теории упругостисмещенийупругих поле -)(rrru деформации тензор-, 2 1 x u напряжений тензор-, zzxyzz yzyyyx xzxyxx }{ c : Гука закон Обобщенный компоненту 813 имеет , постоянныхупругих тензор 4 c cccc объема единице в энергия у пру гая — 2 1 c

Тензор упругих постоянных кристаллов: независимые постоянные для кубической решетки 6, 5, 4, 3, 2, 1 : Фойгта я. Обозначениxyzxyzzzyyxx ) или(, , : независимы такоэффициен три толькокристаллах кубических В 441211 xyxyyzyzxxyyxxxx ссcсcсc 444444111212 121112 121211 00000 000 cccccc ccc c IJ 4412 : впотенциалопарных Для cc

Понятие о теории функционала плотности Hohenberg P. , Kohn W. , 1964 : Все аспекты электронной структуры системы взаимодействующих электронов, находящейся во внешнем потенциальном поле V(r) и невырожденном состоянии, полностью определяются плотностью электронного заряда (r) ( внешнее потенциальное поле в данном случае означает поле ядер). Энергия основного состояния взаимодействующего электронного газа при данном внешнем потенциале является однозначным функционалом функции (r) , и этот функционал минимизируется определенной функцией (r). rd rr rr rdrr. Vr. GE || )()( 2 1 )()()]([][ )]([r. G — функционал кинетической, обменной и корреляционной энергии электронов

Энергия связи твердого тела at ijiii i ji ji св. Erdrd rr rr rd Rr r. Z RR ZZ GE 21 21 21 , || )()( 2 1 || )( ||2 1 ][ i. Zi. R at. E суммирование по i и j производится по ядрам твердого тела, ‑ заряд и радиус-вектор i -го ядра, интегралы берутся по координатам электронов. ‑ суммарная энергия изолированных атомов

Методы описания межатомного взаимодействия, основанные на теории функционала плотности • Метод погруженного атома ( Embedded atom method, EAM) • Метод эффективной среды ( Effective medium theory, EMT) • Потенциал Финниса-Синклера • Клеевая модель Ерколесси ( F. Ercolessi) • …

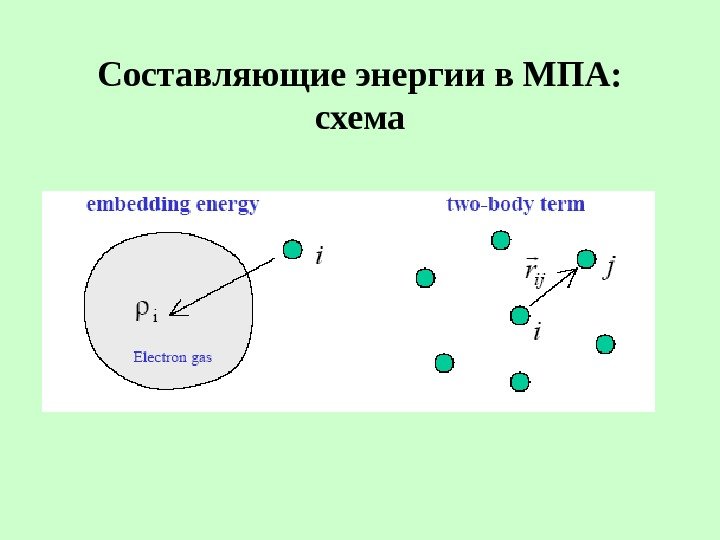
Метод погруженного атома N ij j ijij N i iiiitotr. FEEE 11 )( 2 1 )(, ij ijji. Rf). ( i. F ij f i плотность электронов в узле i энергия внедрения атома i в эту электронную плотность энергия парного взаимодействия между атомами i и j электронная плотность, создаваемая одним атомом

Составляющие энергии в МПА: схема

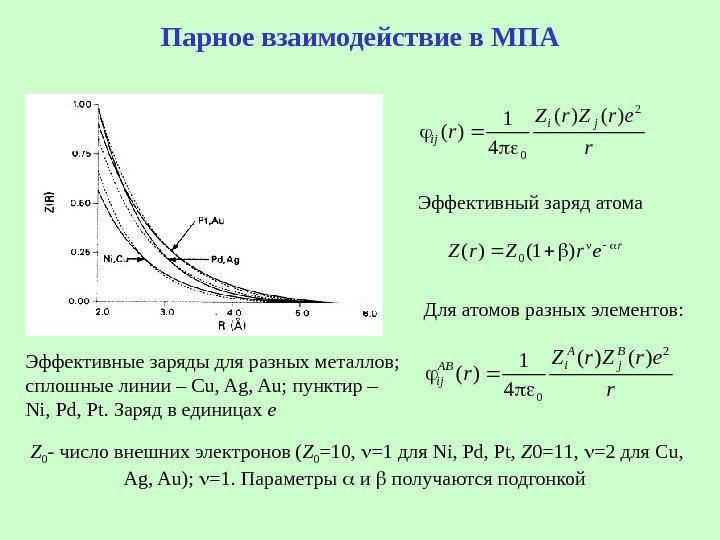
Парное взаимодействие в МПАrer. Z)1()(0 r er. Z r ji ij 2 0 )()( 4 1 )( Эффективный заряд атома Для атомов разных элементов: r er. Z r B j A i. AB ij 2 0 )()( 4 1 )( Эффективные заряды для разных металлов; сплошные линии – Cu, Ag, Au ; пунктир – Ni, Pd, Pt. Заряд в единицах e Z 0 — число внешних электронов ( Z 0 = 10 , =1 для Ni, Pd, Pt, Z 0= 1 1, =2 для Cu, Ag, Au) ; =1. Параметры и получаются подгонкой

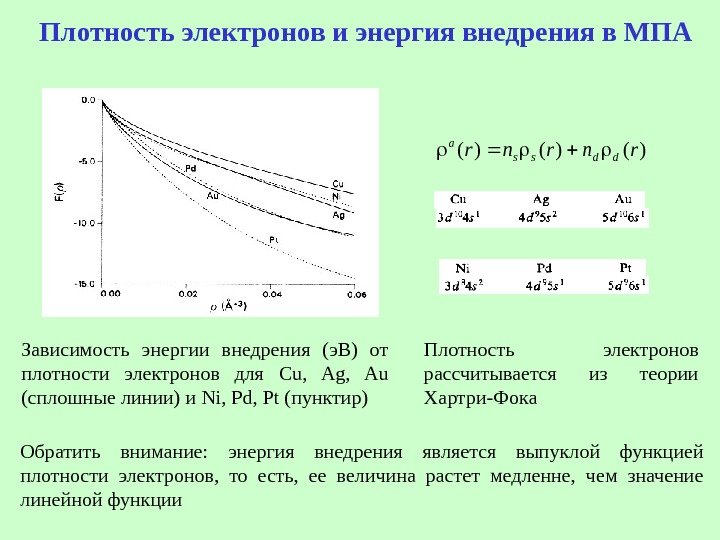
Плотность электронов и энергия внедрения в МПА)()()(rnrnrddss a Зависимость энергии внедрения (э. В) от плотности электронов для Cu, Ag, Au (сплошные линии) и Ni, Pd, Pt (пунктир) Плотность электронов рассчитывается из теории Хартри-Фока Обратить внимание: энергия внедрения является выпуклой функцией плотности электронов, то есть, ее величина растет медленне, чем значение линейной функции

Аналитический потенциал МПА Джонсона (1988); , 1 exp)(c e err r r frf c e err r , 1 exp)( // ln 1)( e e ee св. EF свa. EBV/3 eef 12 ee 6 cer, , , B модуль всестороннего сжатия ‑a. V ‑ атомный объем -параметры, подгоняемые к параметру решетки a или атомному объему V a , энергии связи E св , энергии вакансии E v , модулю всестороннего сжатия B и модулю сдвига G

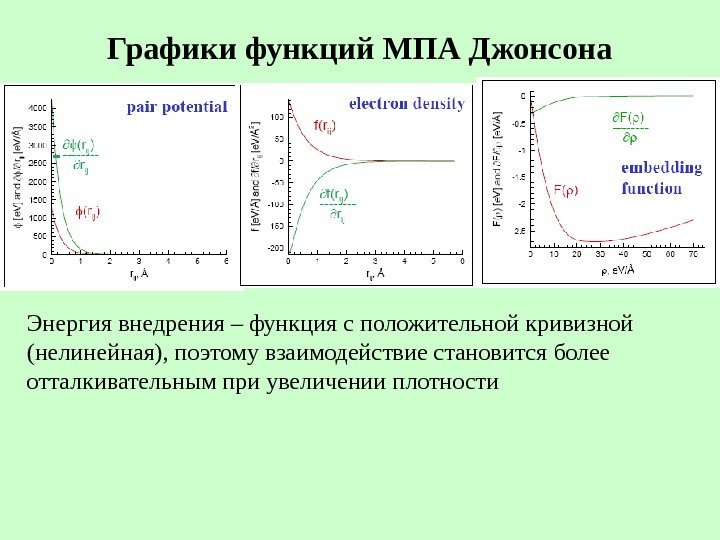
Графики функций МПА Джонсона Энергия внедрения – функция с положительной кривизной (нелинейная), поэтому взаимодействие становится более отталкивательным при увеличении плотности

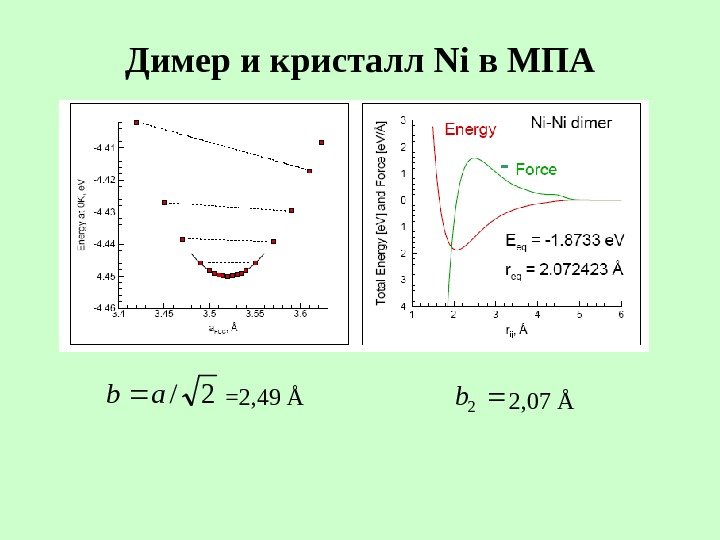
Димер и кристалл Ni в МПА 2/ab =2, 49 Å 2 b 2, 07 Å

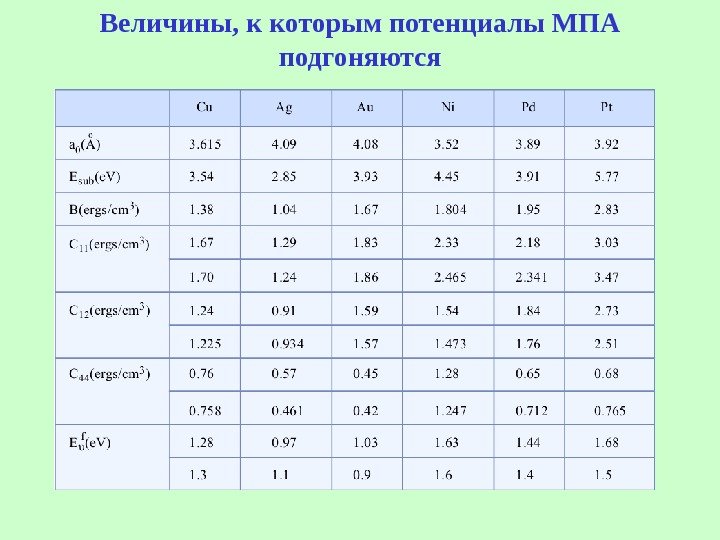
Величины, к которым потенциалы МПА подгоняются

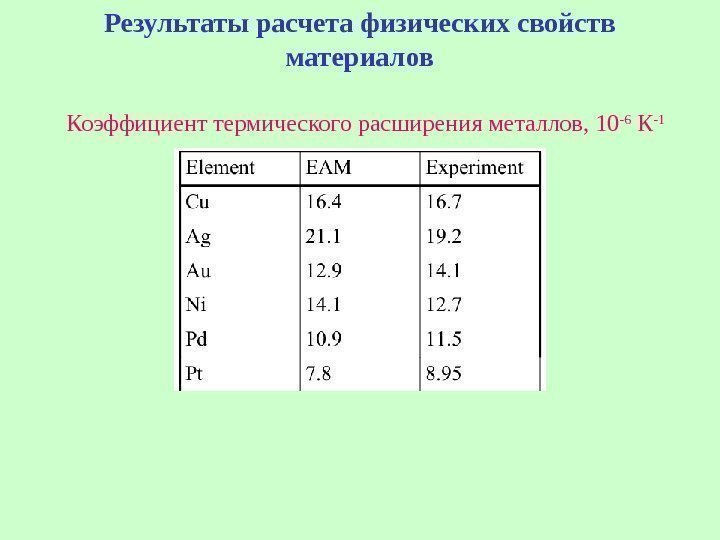
Результаты расчета физических свойств материалов Коэффициент термического расширения металлов, 10 -6 К —

Результаты расчета физических свойств материалов Энергия активации самодиффузии в металлах (в э. В)

Результаты расчета физических свойств материалов Рассчитанные энергии низкоиндексных поверхностей металлов и экспериментальное значение средней энергии поверхности

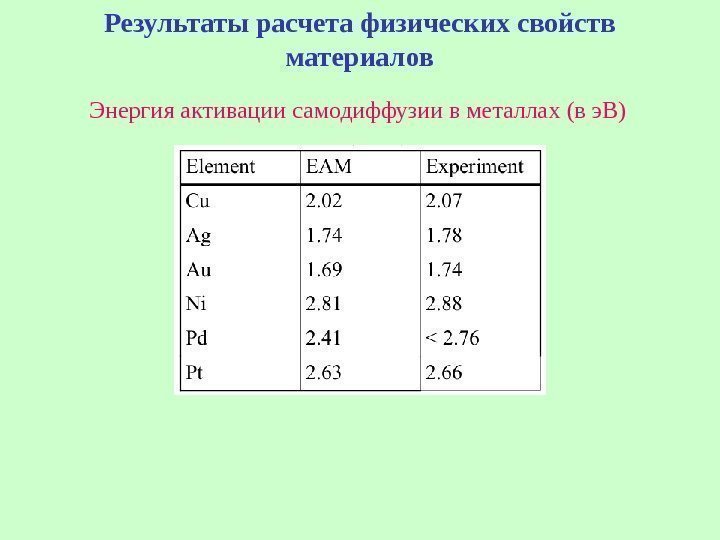
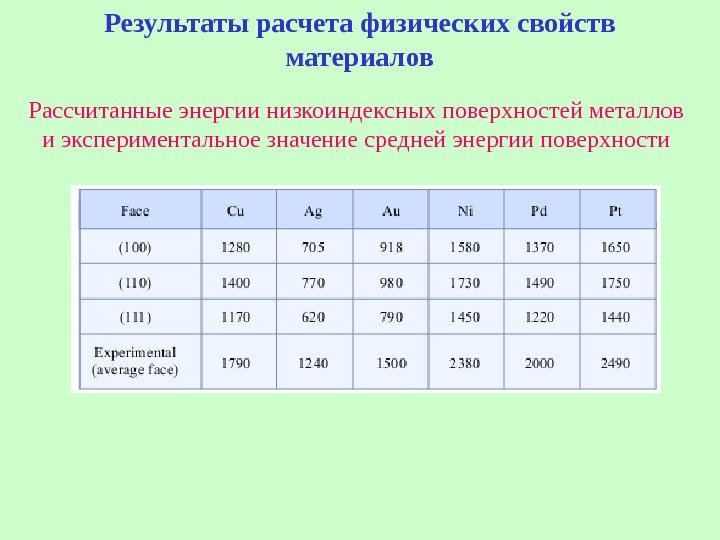
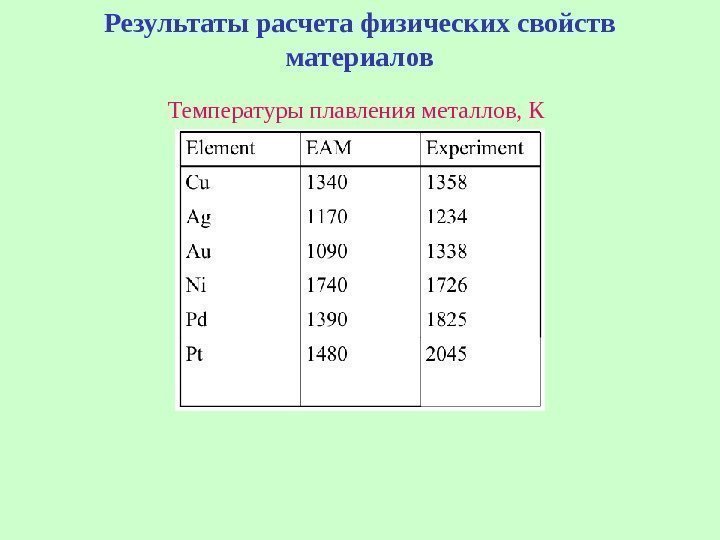
Результаты расчета физических свойств материалов Температуры плавления металлов, К

Таблица потенциала niu 3 для никеля eunit e. V potential set eam 1 potential embed 1 500 0. 000000 0. 250000 0. 00000000 E+00 -0. 5051701604899677 E+00 -0. 7931785384826711 E+00. . . . . -0. 3095312048460391 E+02 -0. 3102562225632869 E+02 potential pair 1 1 499 0. 009697 4. 838788 0. 1454117941298843 E+06 0. 7133742661881313 E+05 0. 4665632980925746 E+05. . . . . 0. 00000000 E+00 potential dens 1 500 0. 000000 4. 838788 0. 00000000 E+00 0. 5901012631981482 E-04 0. 9512300176593089 E-03. . . . . 0. 0000000000000000 E+

Потенциал метода МПА для титана ij ijir)( ij ijiir. FE)()( ii. F)( 8 1 3)()()( i iiirrrrar 4 1 3)()()( i iiirrrrar При >48 При 48 – приближение кубическим сплайном

Таблица потенциала метода МПА для титана # EAM potential for Ti, T. Hammerschmidt et al. PRB 71, 205409 (2005) # Tabulated 26 January 2007 by A. Nazarov # Lattice constants for T=0 K given by XMD: a=2. 9664 A, c=4. 7226 A, c/a=1. 5920 # Reference data: a=2. 965 A, c=4. 721 A, c/a=1. 5920 # Cohesive energy: e 0=-4. 852832 e. V, vacancy formation energy: ef=1. 4246 e. V # Reference data: e 0=-4. 86 e. V, vacancy formation energy: ef=1. 43 e. V # eunit e. V potential set eam 1 # potential pair 1 1 1501 0. 500000 E+00 0. 509113 E+01 0. 753560 E+02 0. 750959 E+02 0. 748364 E+02 0. 745774 E+02. . . . -0. 144189 E-05 -0. 608296 E-06 -0. 180236 E-06 -0. 225295 E-07 0. 000000 E+00 potential dens 1 1501 0. 500000 E+00 0. 509113 E+01 0. 246672 E+03 0. 245784 E+03 0. 244898 E+03 0. 244014 E+03. . . . 0. 100494 E-05 0. 423960 E-06 0. 125618 E-06 0. 157022 E-07 0. 000000 E+00 potential embed 1 1501 0. 000000 E+00 0. 144000 E+03 0. 000000 E+00 -0. 286934 E-01 -0. 571759 E-01 -0. 854506 E-01. . . . -0. 119840 E+02 -0. 119880 E+02 -0. 119920 E+02 -0. 119960 E+02 -0. 120000 E+

Потенциал Клери-Росато (приближение второго момента модели сильной связи) j r r p R i ij Ae. E 1 0 j r r q B i ij e. E 12 20 R i B ii. EEE i i.

Потенциал Финниса-Синклера ij ijirn)( ij iijin. Ar. E)( 2 1 i i.

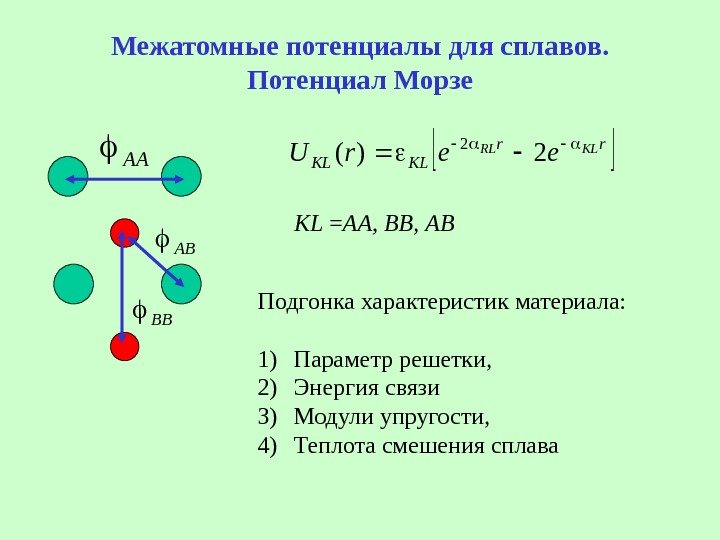
Межатомные потенциалы для сплавов. Потенциал Морзе. AA BB AB rr KLKL KLRLeer. U 2)( 2 KL = АА, ВВ, АВ Подгонка характеристик материала: 1) Параметр решетки, 2) Энергия связи 3) Модули упругости, 4) Теплота смешения сплава

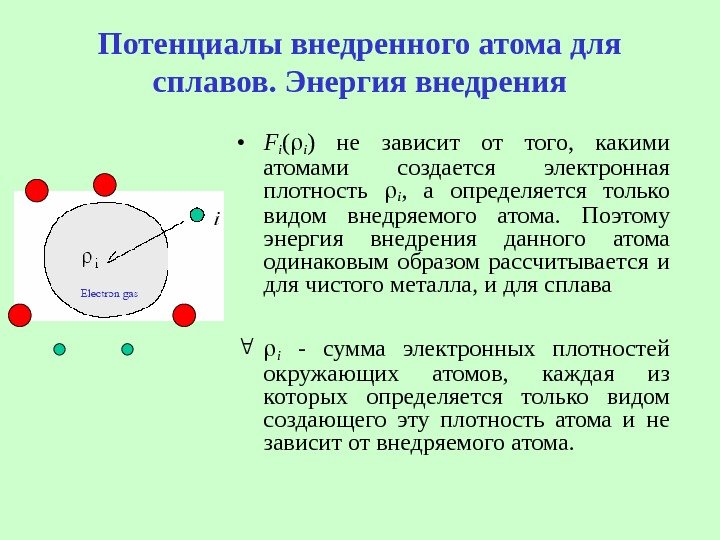
Потенциалы внедренного атома для сплавов. Энергия внедрения • Fi ( i ) не зависит от того, какими атомами создается электронная плотность i , а определяется только видом внедряемого атома. Поэтому энергия внедрения данного атома одинаковым образом рассчитывается и для чистого металла, и для сплава i — сумма электронных плотностей окружающих атомов, каждая из которых определяется только видом создающего эту плотность атома и не зависит от внедряемого атома.

Потенциалы внедренного атома для сплавов. Энергия парного взаимодействияr r. Z r. BA AB )()( )( )( r. Z A )( r. ZB — эффективные заряды атомов А и В r er. Z )1()(0 • Z 0 , подгоночные параметры

Функции, необходимые для двухкомпонентного сплава • Электронные плотности, создаваемые атомами А и В • Энергии внедрения атомов А и В в электронную плотность • Эффективные заряды атомов А и В)(rf. A)(rf. B )(AF)( BF )( r. Z A )( r. Z

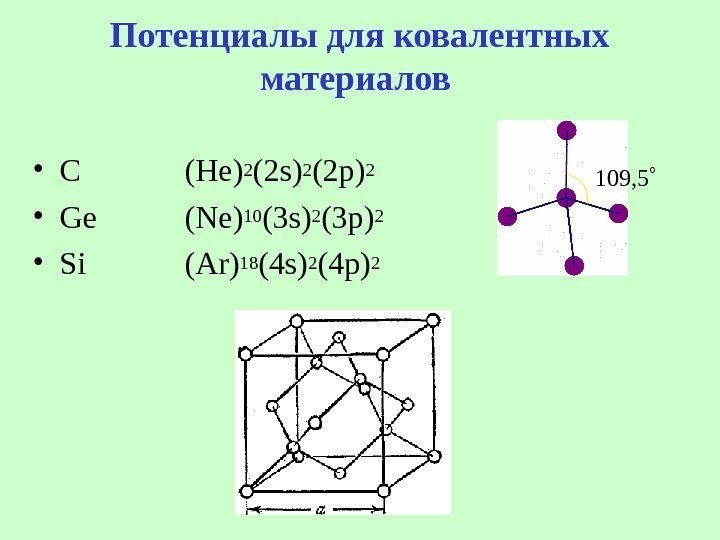
Потенциалы для ковалентных материалов • C (He)2 (2 s)2 (2 p)2 • Ge (Ne) 10 (3 s)2 (3 p)2 • Si (Ar) 18 (4 s)2 (4 p)2 109 ,

Потенциал Стиллингера-Вебера зависящий от угла член проводит к энергетически выгодной кристаллической структуре алмаза с тетраэдрическими углами для Si . . . ), , (), . . . , , (3221 iij kji jkiij ji. Nrrr. Urrr. U cij q ij p ijij rr c r. Br. Ar. Uexp)()(2 ), , (), , (3 ikjkjkiijkjkjijikikijjkikijrrhrrhrrhrrr. U ik j ijk 2 cosexp), , ( jik cikcij jikikij rrrr rrh : 3/147, 109 cos

Недостатки потенциала Стиллингера-Вебера и другие потенциалы • Трехчастичный член определяет только одну равновесную конфигурацию 109. 47 , поэтому его трудно распространить на углерод, для которого существует множество равновесных углов: 180 , 120 и 109. 47 , благодаря чему углерод имеет множество модификаций, как графит, алмаз, фуллерены, нанотрубки и т. д. • Слишком жесткая установка тетраэдрического расположения связей приводит к неправильному описанию релаксации на поверхности и около дефектов, где координация нарушена • Для элементов IV группы были разработаны потенциалы кратной связи ( bond order potentials ), основанные на учете зависимости прочности связи от локального окружения (потенциалы Терсоффа-Абеля для Si и Ge , потенциал Бреннера для C ). Эти потенциалы являются в настоящее время наиболее употребительными при моделировании ковалентных кристаллов

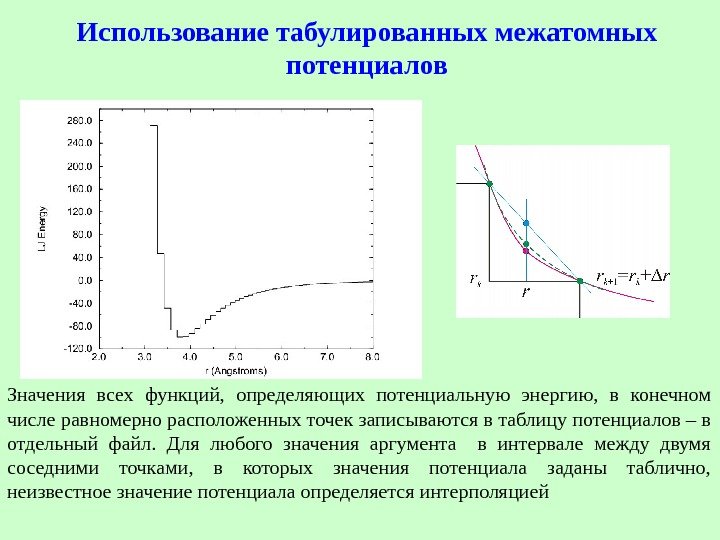
Использование табулированных межатомных потенциалов Значения всех функций, определяющих потенциальную энергию, в конечном числе равномерно расположенных точек записываются в таблицу потенциалов – в отдельный файл. Для любого значения аргумента в интервале между двумя соседними точками, в которых значения потенциала заданы таблично, неизвестное значение потенциала определяется интерполяцией