МЕХАНИКА ТВЕРДОГО ТЕЛА 1 Движение твердого тела Движение

МЕХАНИКА ТВЕРДОГО ТЕЛА 1. Движение твердого тела. Движение центра инерции твердого тела. 2. Момент инерции. Теорема Штейнера. 3. Основное уравнение динамики вращательного движения. 4. Кинетическая энергия твердого тела. Работа внешних сил при вращении твердого тела.

1. Движение твердого тела Два основных вида движения твердого тела — поступательное и вращательное. При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела (например, его центра инерции) для того, чтобы охарактеризовать движение всего тела. При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.

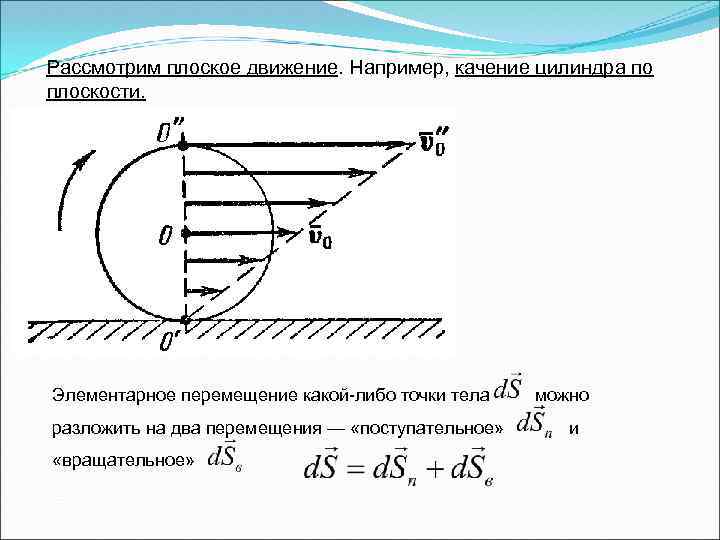Рассмотрим плоское движение. Например, качение цилиндра по плоскости. Элементарное перемещение какой-либо точки тела разложить на два перемещения — «поступательное» «вращательное» можно и

Вращательное перемещение осуществляется поворотом тела на один и тот же угол d (но относительно различных осей). Скорость точки: где - скорость поступательного движения и - скорость, обусловленная вращением. Плоское движение твердого тела можно представить как сумму двух движений — поступательного со скоростью и вращательного с угловом скоростью Линейная скорость точки с радиусомвектором , обусловленная вращением твердого тела, равна

Скорость точки при сложном движении тела может быть представлена в виде: Движение центра инерции твердого тела Рассмотрим систему из N материальных точек. Назовем центром инерции системы точку, положение которой в пространстве задается радиусом-вектором , определяемым следующим образом: где mi – масса i – ой точки; m – масса системы. - радиус-вектор i – ой точки;

Декартовы координаты центра инерции: В однородном поле сил тяжести центр инерции совпадает с центром тяжести системы. Скорость центра инерции: Разобьем тело на элементарные массы mi и представим его как систему материальных точек, взаимное расположение которых неизменно. Если тело находится в поле сил земного тяготения, на каждую элементарную массу тела будет действовать внешняя сила, равная.

Для каждой элементарной массы уравнение второго закона Ньютона: где — результирующая всех внутренних сил, a результирующая всех внешних сил, приложенных к данной элементарной массе. Складывая уравнения для всех элементарных масс, получим: (сумма всех внутренних сил, действующих в системе, равна нулю). - результирующая всех Следовательно: внешних сил, действующих на тело. Сумму в левой части уравнения , можно заменить произведением массы тела m на ускорение его центра инерции.

Действительно, радиус-вектор центра инерции по определению равен: Продифференцировав это соотношение дважды по времени и учитывая, что , а , можно написать: (*) Т. е. центр инерции твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к телу сил. В случае поступательного движения уравнение (*) будет определять ускорение не только центра инерции, но и любой другой точки тела.

При вращательном движении ускорение зависит : 1) не только от силы, но и от расстояния от оси вращения до линии действия силы, т. е. от момента силы. 2) не только от массы, но и от распределения массы относительно оси вращения, т. е. от момента инерции. Т. о. , для изучения вращательного движения необходимо ввести в рассмотрение две новые физические величины — момент силы и момент инерции.

Момент силы относительно точки Моментом силы относительно неподвижной точки О называется векторная величина , определяемая выражением: где - радиус-вектор, проведенный из точки О в точку приложения силы O Направление вектора перпендикулярно плоскости, в которой расположен вектор силы и определяется по правилу правого винта. Момент суммы сил, действующих на точку, равен геометрической сумме моментов слагаемых сил:

Момент пары сил Парой сил называется две равные по величине противоположно направленные силы, не действующие вдоль одной и той же прямой. Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары. Суммарный момент сил Т. к. то и равен - момент пары сил Т. о. , момент пары сил перпендикулярен к плоскости, в которой лежат силы, и численно равен произведению модуля любой из сил на плечо.

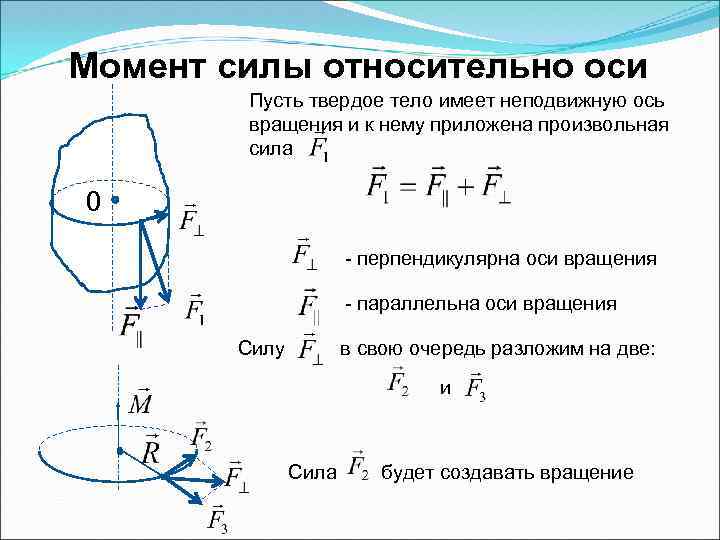Момент силы относительно оси Пусть твердое тело имеет неподвижную ось вращения и к нему приложена произвольная сила 0 - перпендикулярна оси вращения - параллельна оси вращения Силу в свою очередь разложим на две: и Сила будет создавать вращение

2. Момент инерции. Теорема Штейнера. Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведений масс материальных точек системы на квадрат их расстояний до рассматриваемой оси. В пределе сумма сводится к интегралу:

Найдем момент инерции однородного диска. О’ О Объем слоя R dr r h О’ О

О’ О R dr r h О’ Теорема Штейнера: Момент инерции J относительно произвольной оси равен сумме момента инерции J 0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния a между осями: О Определим момент инерции диска относительно оси O’O’ :

Моменты инерции различных тел 1) Момент инерции материальной точки с массой m, расположенной на расстоянии r от оси: r m 2) Момент инерции однородного кольца или тонкостенного цилиндра относительно оси симметрии: R 3) Момент инерции однородного шара относительно оси, проходящей через центр: R 4) Момент инерции стержня относительно оси, проходящей через его середину, перпендикулярно к его длине :

3. Основное уравнение динамики вращательного движения Уравнение второго закона Ньютона для тангенциальной составляющей силы: где - плечо силы Но следовательно Основное уравнение динамики вращательного движения

Поступательное движение Вращательное движение Масса Момент инерции Линейная скорость Угловая скорость Линейное ускорение Угловое ускорение Сила Момент силы Импульс Момент импульса Работа при поступательном движении: Кинетическая энергия поступательного движения: Работа при вращении: Кинетическая энергия вращательного движения:

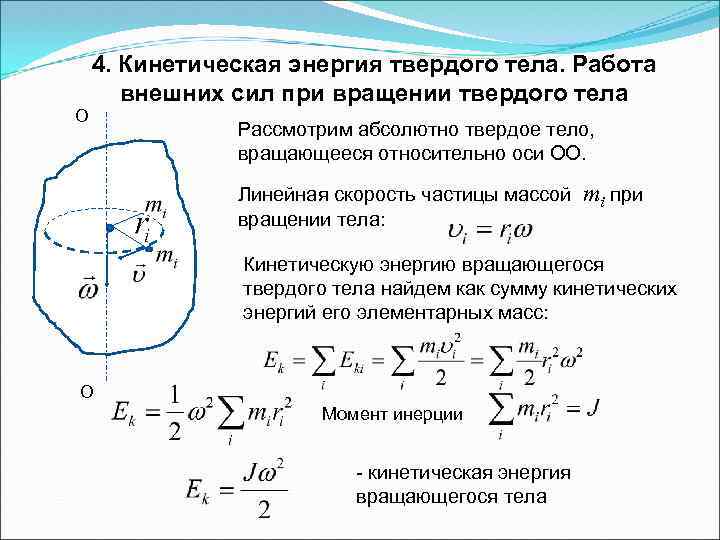4. Кинетическая энергия твердого тела. Работа внешних сил при вращении твердого тела О Рассмотрим абсолютно твердое тело, вращающееся относительно оси ОО. Линейная скорость частицы массой вращении тела: mi при Кинетическую энергию вращающегося твердого тела найдем как сумму кинетических энергий его элементарных масс: О Момент инерции - кинетическая энергия вращающегося тела

Для тела, катящегося по горизонтальной поверхности: m – масса катящегося тела, - скорость поступательного движения, J – момент инерции тела, - скорость вращательного движения. Работа внешних сил при вращении твердого тела О - внешняя сила, приложенная к элементарной массе - путь за время dt О

1. Момент количества движения 2. Закон сохранения момента количества движения 3. Свободные оси. Главные оси инерции 4. Гироскопы

1. Момент количества движения (момент импульса) Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: (*) О А где — радиус-вектор, проведенный из точки О в точку A, — импульс материальной точки - вектор момента количества движения Введем плечо Модуль вектора момента количества движения

Определим изменение момента импульса со временем. Продифференцируем выражение (*) по времени t. Т. о. производная от момента импульса равна моменту силы. - импульс момента силы. - ещё одна форма закона динамики вращательного движения твердого тела относительно неподвижной оси.

Определим момент количества движения тела О Тело вращается вокруг оси ОО с угловой скоростью Т. к. то - момент инерции тела Момент количества движения твердого тела О Продифференцируем по времени:

2. Закон сохранения момента количества движения 1. Если момент всех внешних сил, действующих на тело, равен нулю, то Закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остается постоянным. 2. Если результирующий момент внешних сил составляющая вектора , однако равна 0 по некоторому направлению z, то:

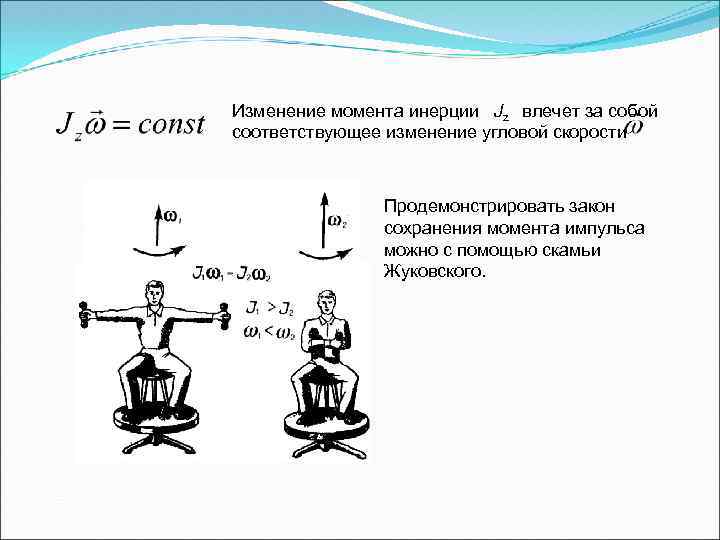Изменение момента инерции Jz влечет за собой соответствующее изменение угловой скорости Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского.

3. Свободные оси. Главные оси инерции О Ось вращения, положение которой в пространстве сохраняется без действия на нее каких-либо сил извне, называется свободной осью тела. О Для удержания произвольной оси неподвижной к ней необходимо приложить определенные силы.

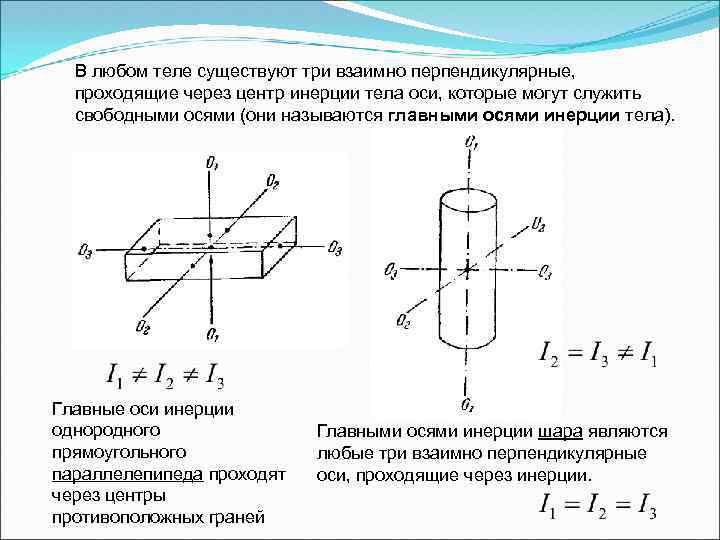В любом теле существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями (они называются главными осями инерции тела). Главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней Главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через инерции.

Вращение вокруг главных осей устойчиво без внешнего воздействия. Если тело вращается в условиях, когда воздействие извне отсутствует, то устойчивым оказывается только вращение вокруг главных осей, соответствующих максимальному и минимальному значениям момента инерции. Вращение же вокруг оси, соответствующей промежуточному по величине моменту, будет неустойчивым. При наличии внешнего воздействия, например, со стороны нити, за которую подвешено вращающееся тело, устойчивым оказывается только вращение вокруг главной оси, соответствующей наибольшему значению момента инерции.

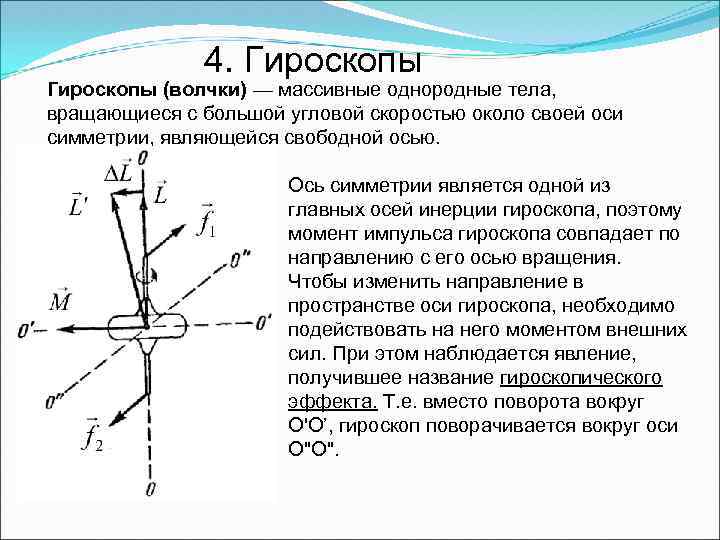4. Гироскопы (волчки) — массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью. Ось симметрии является одной из главных осей инерции гироскопа, поэтому момент импульса гироскопа совпадает по направлению с его осью вращения. Чтобы изменить направление в пространстве оси гироскопа, необходимо подействовать на него моментом внешних сил. При этом наблюдается явление, получившее название гироскопического эффекта. Т. е. вместо поворота вокруг О'О’, гироскоп поворачивается вокруг оси О"О".

За время t под действием момента сил и момент импульса гироскопа получит приращение , которое имеет такое же направление, как и. Момент импульса гироскопа спустя время t будет равен Направление вектора совпадает с новым направлением оси вращения гироскопа О"О", причем угол между векторами М и L уменьшается. Если действовать на гироскоп длительное время постоянным по направлению моментом внешних сил , то ось гироскопа устанавливается в конце концов так, что вектор совпадает по направлению с вектором. Описанное поведение гироскопа положено в основу прибора, называемого гироскопическим компасом (гирокомпасом).