МЕХАНИКА. Кинематика материальной точки КРАТКОЕ СОДЕРЖАНИЕ 1

МЕХАНИКА. Кинематика материальной точки КРАТКОЕ СОДЕРЖАНИЕ 1

Механическая картина мира сформировалась к середине XIX века. Согласно этой картине все тела состоят из мельчайших частиц, «кирпичиков» мироздания, - атомов и молекул. Основой картины мира являются законы Ньютона. Мир представляет собой гигантскую машину, построенную по законам механики. Микромир считался подобным макромиру. Природа абсолютно неизменна. В мире господствуют однозначные причинно-следственные связи (лапласовский детерминизм). В XIX веке механическая картина мира сменилась электромагнитной. Механическое движение — это изменение с течением времени взаимного расположения тел или их частей Механика — раздел физики, который изучает закономерности механического движения и причины, вызывающие или изменяющие это движение МЕХАНИКА ( «механэ» - машина, механизм (греч. )) Кинематика «кинема» движение (греч. ) Динамика «динамис» - сила (греч. ) Статика «статон» - стоящий (греч. ) 2

Кинематика материальной точки Кинематика - изучает движение тел, не рассматривая причин, которые это движение вызывают Материальная точка – одна из физических моделей Материальной точкой называют тело, размеры и форма которого в данной задаче не существенны. Материальную точку часто называют телом. Привести примеры, когда одно и то же тело можно считать материальной точкой , и когда нельзя. 3

Система координат – это способ задания математических переменных, которые однозначно задают положение точки в пространстве Наиболее часто используемые системы координат: - прямоугольная декартова система координат; - полярная система координат (на плоскости); - сферическая система координат (в пространстве) Рене Декарт (1596 -1650) – французский математик, физик, философ и военный 4

Рене Дека рт (фр. René Descartes) (1596 - 1650) — французский математик, философ, физик и физиолог, создатель аналитической геометрии 5

Тело отсчета – это тело, относительно которого рассматривается движение всех остальных тел Система отсчета = 1) тело отсчета + 2) система координат, связанная с телом отсчета, + 3) часы (прибор для измерения времени движения с указанием на начало его отсчета) Система отсчета используется для определения положения в пространстве физических объектов в различные моменты времени. Различают инерциальные и неинерциальные системы отсчета 6

Основные понятия кинематики материальной точки Радиус-вектор точки. Декартовы координаты (x, y, z) определяют в пространстве радиусвектор r, острие которого описывает при его изменении со временем траекторию материальной точки. Закон движения (кинематические уравнения движения) – зависимость радиус-вектора материальной точки (или ее координат) от времени Траектория — линия, описываемая точкой при ее движении в пространстве. В случае движения по плоскости это – y = y(x) В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Примеры криволинейного движения: движение тела, брошенного под углом к горизонту (траектория – парабола), движение материальной точки по окружности. 7

Перемещением называется вектор, проведенный из начальной в конечную точку траектории. Путь к моменту времени t. Длина траектории точки от t = 0 представляет собой величину пройденного пути S(t). Путь S(t) - скалярная величина Приращение пути равно модулю вектора перемещения лишь в случае прямолинейной траектории 8

Средняя скорость В системе СИ : [v] = 1 м/с Мгновенная скорость Это векторная величина, определяемая как предел отношения перемещения точки к промежутку времени, за который это перемещение произошло, когда этот промежуток времени стремится к нулю Вектор мгновенной скорости всегда направлен по касательной к траектории тела Проекции скорости тела на оси координат по теореме Пифагора 9

Ускорение – это векторная величина, характеризующая быстроту изменения скорости. При произвольном движении ускорение определяется как отношение приращения Δv скорости к соответствующему промежутку времени Δt. Такое ускорение называется средним Мгновенное ускорение. Если устремить этот промежуток времени к нулю, получим мгновенное ускорение. Значит, ускорение есть производная от скорости по времени (и вторая производная от радиус-вектора). Проекции ускорения на оси координат по теореме Пифагора 10

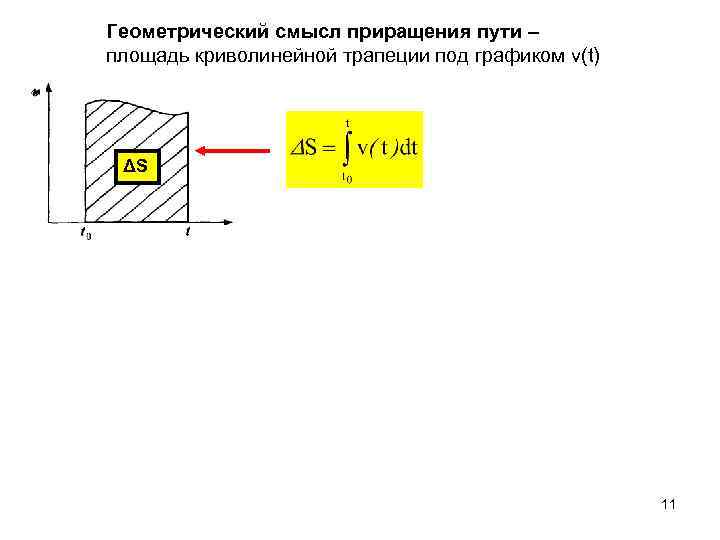Геометрический смысл приращения пути – площадь криволинейной трапеции под графиком v(t) ΔS 11

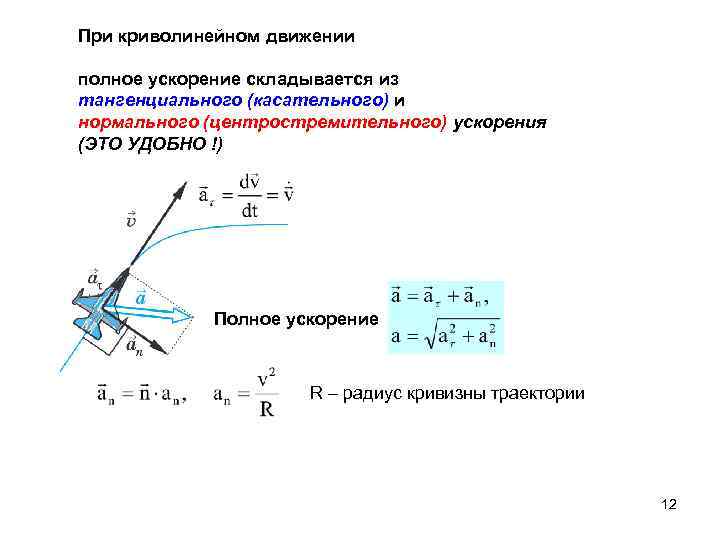При криволинейном движении полное ускорение складывается из тангенциального (касательного) и нормального (центростремительного) ускорения (ЭТО УДОБНО !) Полное ускорение R – радиус кривизны траектории 12

Равномерное движение – это движение, при котором за любые равные промежутки времени материальная точка проходит одинаковые пути. Равномерное прямолинейное движение – это то же самое, что и равномерное движение, если траектория тела – прямая линия при этом a = 0, v = const Закон равномерного движения материальной точки вдоль оси x x(t) = x 0 + vt , v = const, a = 0 (x 0 - начальная координата, t — время) 13

Равнопеременное движение Это есть движение вдоль прямой с постоянным ускорением а= const Делится на два вида: равноускоренное и равнозамедленное Равноускоренное движение Равнозамедленное движение При начальном движении точки вдоль оси x (x 0 , v 0 - начальные координата и скорость, t – время) Скорость Координата + для случая равноускоренного движения, - для случая равнозамедленного движения «временная» и «безвременная» формулы 14

Пример равнопеременного движения – движение тела, брошенного вертикально в поле силы тяжести Земли Основные модельные предположения: 1) сила тяжести – единственная сила, действующая та тело (нет сопротивления воздуха, ветра); 2) поле силы тяжести однородно и вертикально; 3) масса тела не меняется в процессе полета В этом случае и направлено всегда вниз. Таким образом, движение вверх (до высшей точки траектории) – равнозамедленное, а вниз – равноускоренное. Если ось «у» направить вверх и принять y = 0, t = 0 на поверхности Земли, то Важно: эти формулы справедливы на обеих стадиях полета тела – вверх и вниз 15

СПРАВКА: Ускорение свободного падения Ускорение свободно падающего тела - ускорение, с которым движется тело под действием силы тяжести. Ускорение свободного падения одинаково для всех тел, независимо от их массы. На Земле ускорение свободно падающего тела зависит от высоты над уровнем моря, от географической широты, а также от других факторов (пример: залежи железной руды). На широте 450 и на уровне моря ускорение свободно падения g=g 0 = 9. 80665 м/с2. В учебных задачах обычно полагают g=g 0 = 9, 81 м/с2 10 м/с2. 16

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ Поступательное движение — движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Любое криволинейное движение можно представить как последовательное движение по дугам окружностей переменного радиуса кривизны R(t). Тангенциальное (касательное) ускорение a Тангенциальное ускорение - составляющая ускорения, направленная по касательной к траектории движения в данной точке. Тангенциальное ускорение характеризует изменение скорости по модулю. Нормальное (центростремительное) ускорение an Нормальное ускорение - составляющая ускорения, направленная вдоль нормали к траектории движения в данной точке. Нормальное ускорение характеризует изменение скорости по направлению 17

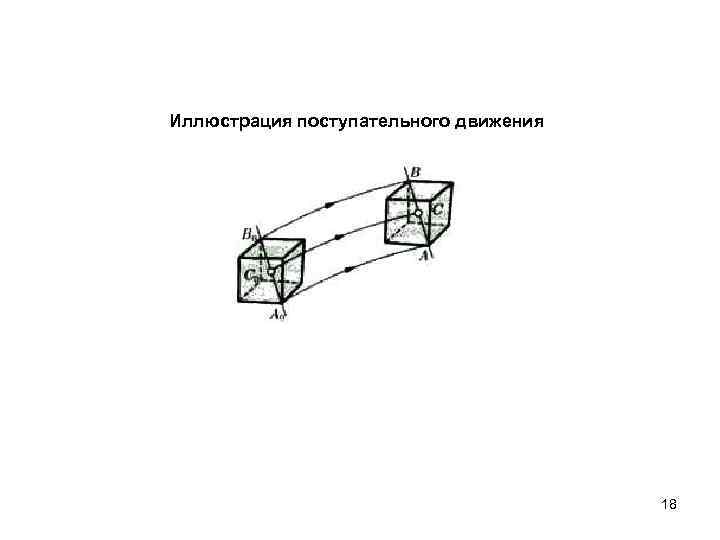Иллюстрация поступательного движения 18

Вращательное движение по окружности Угловая скорость - векторная величина, характеризующая вращательное движение твердого тела и направленная по оси вращения согласно правилу буравчика (правого винта ). Средняя угловая скорость численно равна отношению угла поворота к соответствующему промежутку времени. Единицей угловой скорости в СИ является [рад/с]. Мгновенная угловая скорость - предел, к которому стремится средняя угловая скорость при бесконечном уменьшении промежутка времени. Мгновенная угловая скорость - производная от угла поворота по времени: Линейная скорость - скорость отдельной точки вращающегося тела, зависящая от угловой скорости и расстояния от точки до оси вращения. Линейная скорость материальной точки численно равна расстоянию, которое точка проходит в единицу времени. Равномерное вращательное движение - движение, при котором углы поворота материальной точки за любые равные промежутки времени одинаковы 19

Время, за которое тело совершает полный оборот, т. е. поворачивается на угол 2π, называется периодом вращения Т. Угловая (круговая, или циклическая) частота вращения [рад/с] – это модуль угловой скорости Обычная частота вращения – это число оборотов тела в единицу времени СИ: [ ] = 1 c-1 = 1 Гц , [ ] = 1 рад/с Закон движения для равномерного вращения ( 0 - начальное угловое перемещение, t - время, =const ) 20

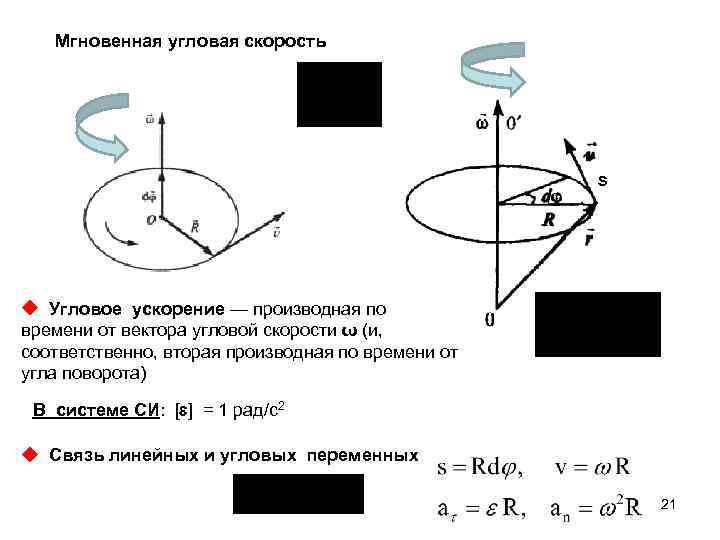Мгновенная угловая скорость s Угловое ускорение — производная по времени от вектора угловой скорости ω (и, соответственно, вторая производная по времени от угла поворота) В системе СИ: [ ] = 1 рад/с2 Связь линейных и угловых переменных 21

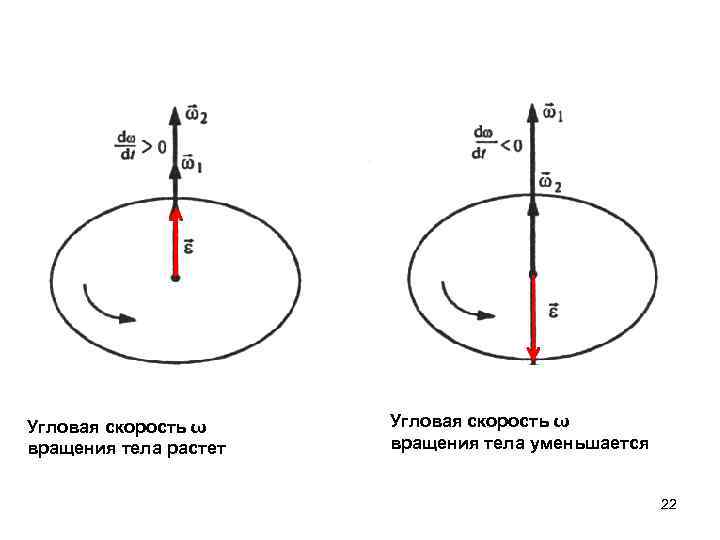Угловая скорость ω вращения тела растет Угловая скорость ω вращения тела уменьшается 22

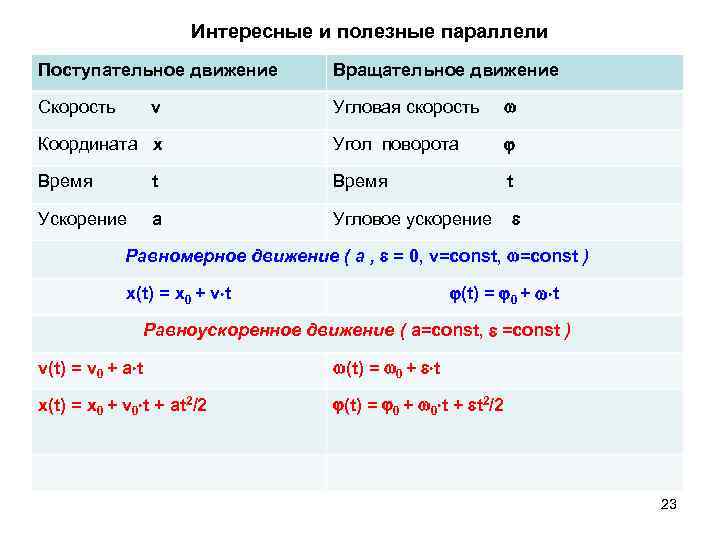Интересные и полезные параллели Поступательное движение Вращательное движение Скорость Угловая скорость Координата х Угол поворота Время t Ускорение a Угловое ускорение v Равномерное движение ( a , = 0, v=const, =const ) (t) = 0 + t x(t) = x 0 + v t Равноускоренное движение ( a=const, =const ) v(t) = v 0 + a t (t) = 0 + t x(t) = x 0 + v 0 t + at 2/2 (t) = 0 + 0 t + t 2/2 23

Прямая и обратная задачи кинематики материальной точки Прямая задача кинематики заключается в определении скорости по заданной зависимости радиус-вектора или координат от времени, а также в определении ускорения по известной зависимости скорости от времени. Обратная задача кинематики заключается в определении скорости v(t) по заданной зависимости a(t) ускорения от времени и в определении радиус-вектора или координат x(t), y(t), z(t) по известной зависимости скорости от времени v(t) 24

Сложение движений. Относительность движения. Принцип относительности классической механики (принцип относительности Галилея) Принцип относительности классической механики – постулат Галилея, согласно которому в любых инерциальных системах отсчета все механические явления протекают одинаково при одних и тех же условиях. ИЛИ: по отношению к разным инерциальным системах отсчета скорость относительна, а ускорение - абсолютно Относительное движение - движение точки или тела относительно движущейся системы отсчета Преобразования Галилея - соотношения, позволяющие переходить (в классической механике) от пространственно-временных координат некоторого события в одной инерциальной системе отсчета к пространственно-временным координатам этого же события в другой инерциальной системе отсчета 25

Галилео-Галилей (1564 -1642) - итальянский ученый, физик, механик и астроном, один из основоположников естествознания; поэт, филолог и критик 26

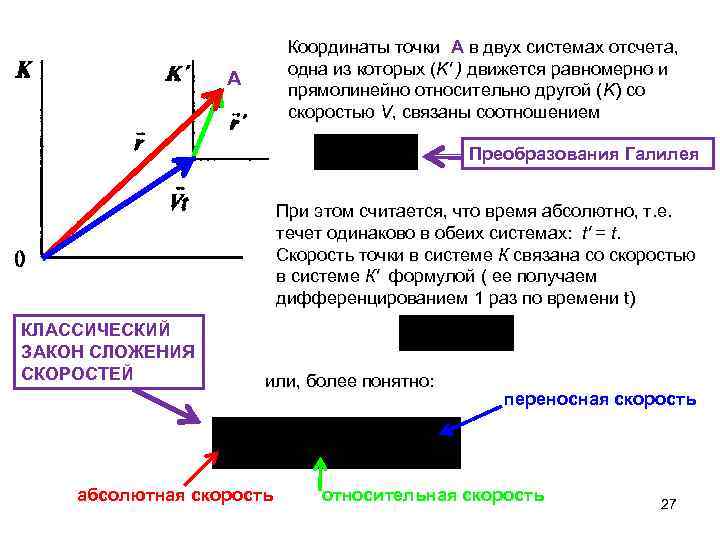Координаты точки А в двух системах отсчета, одна из которых (K' ) движется равномерно и прямолинейно относительно другой (K) со скоростью V, связаны соотношением А Преобразования Галилея При этом считается, что время абсолютно, т. е. течет одинаково в обеих системах: t' = t. Скорость точки в системе К связана со скоростью в системе К' формулой ( ее получаем дифференцированием 1 раз по времени t) КЛАССИЧЕСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ или, более понятно: абсолютная скорость переносная скорость относительная скорость 27

В покоординатной форме преобразования Галилея имеют вид 28

29