МЕХАНИКА Кинематика Динамика Статика Законы сохранения в механике

МЕХАНИКА Кинематика Динамика Статика Законы сохранения в механике Механические колебания и волны

Кинематика 1. Механическое движение и его виды 2. Относительность механического движения 3. Скорость. 4. Ускорение. 5. Равномерное движение. 6. Прямолинейное равноускоренное движение. 7. Свободное падение (ускорение свободного падения). 8. Движение тела по окружности с постоянной по модулю скоростью. Центростремительное ускорение.

Динамика 1. Инерциальные системы отсчета. Первый закон Ньютона 2. Принцип относительности Галилея 3. Масса тела. 4. Плотность вещества. 5. Сила. 6. Принцип суперпозиции сил. 7. Второй закон Ньютона. 8. Третий закон Ньютона. 9. Закон всемирного тяготения. Искусственные спутники Земли. 10. Сила тяжести. 11. Вес и невесомость. 12. Сила упругости. Закон Гука. 13. Сила трения. 14. Давление

Статика 1. Момент силы 2. Условия равновесия твердого тела 3. Давление жидкости 4. Закон Паскаля 5. Закон Архимеда 6. Условия плавания тел

Законы сохранения в механике 1. Импульс тела 2. Импульс системы тел 3. Закон сохранения импульса 4. Работа силы 5. Мощность 6. Работа как мера изменения энергии 7. Кинетическая энергия 8. Потенциальная энергия 9. Закон сохранения механической энергии

Механические колебания и волны 1. Гармонические колебания 2. Амплитуда и фаза колебаний 3. Период колебаний 4. Частота колебаний 5. Свободные колебания (математический и пружинный маятники) 6. Вынужденные колебания 7. Резонанс 8. Длина волны 9. Звук

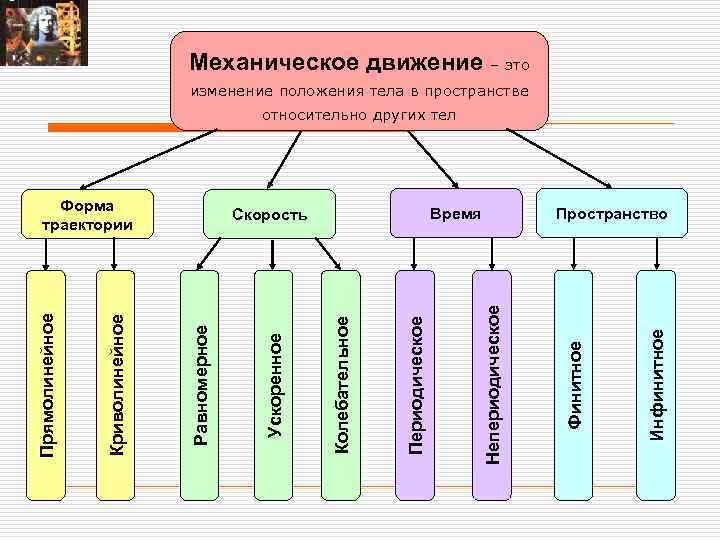Механическое движение – это изменение положения тела в пространстве относительно других тел Инфинитное Финитное Периодическое Колебательное Ускоренное Пространство Непериодическое Время Скорость Равномерное Криволинейное Прямолинейное Форма траектории

Описание механического движения Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t), либо при помощи зависимости от времени радиус-вектора, проведенного из начала координат до данной точки. Перемещением тела называют направленный отрезок прямой, начальное положение тела с его последующим положением. соединяющий Пройденный путь равен длине дуги траектории, пройденной телом за некоторое время. Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.

Относительность механического движения Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда. Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными.

Относительность механического движения Пусть имеются две системы отсчета. Система XOY условно считается неподвижной, а система X'O'Y' движется поступательно по отношению к системе XOY со скоростью v 0. Система XOY может быть, например, связана с Землей, а система X'O'Y' – с движущейся по рельсам платформой. Пусть человек перешел по платформе из точки A в точку B. Тогда его перемещение, скорость и ускорение относительно Земли соответствуют векторам

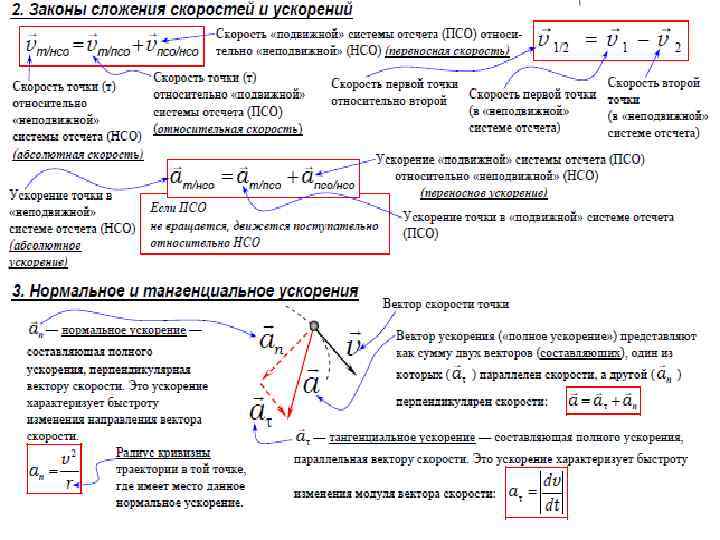
Скорость Для характеристики движения вводится понятие средней скорости. Средняя скорость – физическая величина, равная отношению перемещения тела к промежутку времени, в течение которого произошло это перемещение. Мгновенная скорость – это физическая величина, к которой стремится средняя скорость при неограниченном уменьшении промежутка времени, включающая данный момент: При криволинейном движении мгновенная скорость тела в каждой точке траектории направлена по касательной к траектории в этой точке.

Скорость При движении тела по криволинейной траектории его скорость изменяется по модулю и направлению. Изменение вектора скорости за некоторый малый промежуток времени Δt можно задать с помощью вектора Вектор изменения скорости за малое время . Δt можно разложить на две составляющие: направленную вдоль вектора составляющая), и направленную перпендикулярно вектору составляющая). (касательная (нормальная

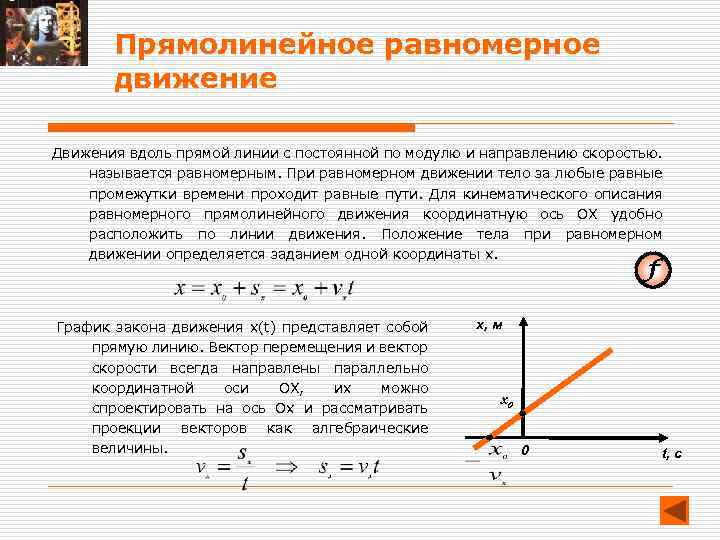Прямолинейное равномерное движение Движения вдоль прямой линии с постоянной по модулю и направлению скоростью. называется равномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. График закона движения x(t) представляет собой прямую линию. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX, их можно спроектировать на ось Oх и рассматривать проекции векторов как алгебраические величины. х, м x 0 0 t, c

Ускорением тела называют предел отношения малого изменения скорости к малому промежутку времени, в течение которого происходило изменение скорости: Направление вектора ускорения в случае криволинейного движения не совпадает с направлением вектора скорости. Составляющие вектора ускорения называют касательным (тангенциальным) и нормальным ускорениями Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю, а нормальное – насколько быстро скорость тела изменяется по направлению.

Ускорение Криволинейное движение можно представить как движение по дугам окружностей Нормальное ускорение зависит от модуля скорости и от радиуса окружности, по дуге которой тело движется в данный момент: Вектор всегда направлен к центру окружности. Модуль полного ускорения равен

Прямолинейное равноускоренное движение Движение вдоль прямой линии, при котором тело за равные промежутки времени изменяет свою скорость одинаково, называется прямолинейным равноускоренным. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения, следовательно, скорость и ускорение в проекциях на направление движения можно рассматривать как алгебраические величины. При равноускоренном прямолинейном движении скорость тела определяется формулой В этой формуле: – скорость тела при a = const – ускорение. t = 0 (начальная скорость),

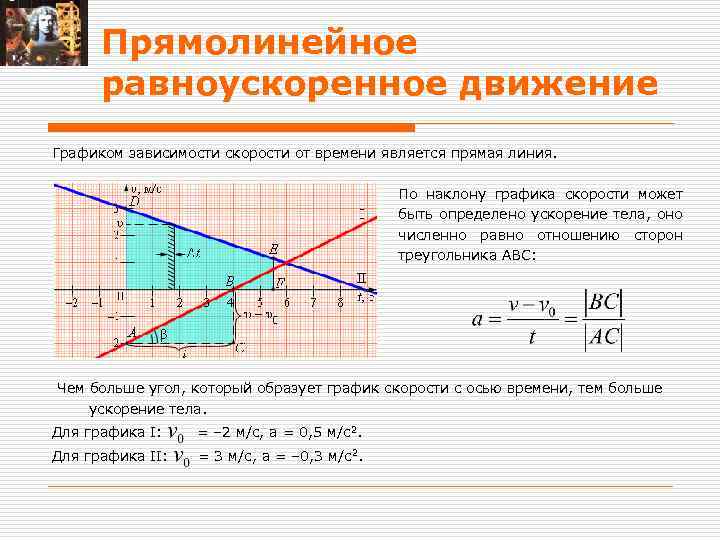Прямолинейное равноускоренное движение Графиком зависимости скорости от времени является прямая линия. По наклону графика скорости может быть определено ускорение тела, оно численно равно отношению сторон треугольника ABC: Чем больше угол, который образует график скорости с осью времени, тем больше ускорение тела. Для графика I: = – 2 м/с, a = 0, 5 м/с2. Для графика II: = 3 м/с, a = – 0, 3 м/с2.

Прямолинейное равноускоренное движение График скорости позволяет также определить проекцию перемещения тела за некоторое время t, оно равно площади трапеции ODEF. Для нахождения координаты тела в любой момент времени нужно к начальной координате х0 прибавить перемещение за время t: Перемещение можно найти по безвременной формуле:

Свободное падение Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха. Это частный случай равноускоренного движения. Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение оказывается неодинаковым, изменяясь примерно от 9, 83 м/с2 на полюсах до 9, 78 м/с2 на экваторе. Если в расчетах не требуется высокая точность, то числовое значение у поверхности Земли принимают равным 9, 8 м/с2 или даже 10 м/с2. Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, тогда: v 0 = 0, y 0 = h, a = –g.

Свободное падение Если тело при падении оказалось в точке с координатой y < h, то перемещение s тела равно s = y – h < 0. Эта величина отрицательна, так как тело при падении перемещалось навстречу выбранному положительному направлению оси OY. В результате получим: Скорость отрицательна, так как вектор скорости направлен вниз. Время падения tп тела на Землю найдется из условия y = 0:

Свободное падение Скорость тела в любой точке составляет: В частности, при y = 0 скорость падения тела на Землю равна: Пользуясь этими формулами, можно вычислить время падения тела с данной высоты, скорость падения тела в любой момент после начала падения и в любой точке его траектории и т. д. Аналогичным образом решается задача о движении тела, брошенного вертикально вверх с некоторой начальной скоростью. Если ось OY по-прежнему направлена вертикально вверх, а ее начало совмещено с точкой бросания, то в формулах равноускоренного прямолинейного движения следует учесть:

Свободное падение Через время скорость тела обращается в нуль, т. е. тело достигает высшей точки подъема. Зависимость координаты y от времени t выражается формулой Тело возвращается на землю (y = 0) через время следовательно, время подъема и время падения одинаковы. Во время падения на землю скорость тела равна , т. е. тело падает на землю с такой же по модулю скоростью, с какой оно было брошено вверх.

Свободное падение Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось OY) направить вертикально вверх, а другую (ось OX) – расположить горизонтально. Тогда движение тела по криволинейной траектории можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси OY и равномерного прямолинейного движения вдоль оси OX. Для движения вдоль оси следующие условия: Для движения вдоль оси OY: OX будут

Свободное падение Время полета: Дальность полета: Максимальная высота подъема:

Движение тела по окружности с постоянной по модулю скоростью Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах. Длина дуги связана с углом поворота соотношением. При малых углах поворота Угловой скоростью ω тела в данной точке называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt: Угловая скорость измеряется в рад/с. Связь между модулем линейной скорости и угловой скоростью:

Центростремительное ускорение Равномерное движение тела по окружности является движением с ускорением. Ускорениена правлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной и угловой скоростями соотношениями: При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру.

Взаимодействие тел. Сила. Принцип суперпозиции сил Причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. В процессе взаимодействия оба тела приобретают ускорения. Массы взаимодействующих тел обратно пропорциональны ускорениям, приобретаемым телами в результате их взаимодействия: Сила – это количественная мера взаимодействия тел, она является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую природу: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей сил.

Первый закон Ньютона. Инерциальные системы отсчета Так как движение и покой относительны, то в различных системах отсчета движение тела будет разным. В одной системе отсчета тело может находиться в покое или двигаться с постоянной скоростью, в другой системе это же тело может двигаться с ускорением. Существуют системы отсчета, называемые инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел скомпенсированы. При описании движения тел вблизи поверхности Земли системы отсчета, связанные с Землей, приближенно можно считать инерциальными. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы. Все инерциальные системы отсчета равноправны. Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции.

Второй закон Ньютона. Масса тела. Плотность вещества Ускорение тела прямо пропорционально действующей силе, приложенной к телу, и обратно пропорционально его массе: Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой. В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг). Масса тела – скалярная величина. Опыт показывает, что если два тела с массами m 1 и m 2 соединить в одно, то масса m составного тела оказывается равной: m = m 1 + m 2. Это свойство масс называют аддитивностью. Массу можно рассчитать через плотность вещества: m = ρV. Второй закон Ньютона справедлив только в инерциальных системах отсчета.

Третий закон Ньютона В инерциальных системах отсчета все силы появляются или исчезают только парами. Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.

Закон всемирного тяготения. Сила тяжести. Невесомость Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними: G = 6, 67· 10– 11 Н·м 2/кг 2 – гравитационная постоянная, одинаковая для всех тел во Вселенной. Действием сил всемирного тяготения объясняется движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли и т. д. Закон всемирного тяготения может быть применен для расчета сил взаимодействия между материальными точками, однородными телами шарообразной формы, одно тело – шар большого радиуса, другое – маленькое любой формы.

Закон Всемирного тяготения. Сила тяжести. Невесомость Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна: где g – ускорение свободного падения у поверхности Земли: Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения, находясь при этом в состоянии невесомости. При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9, 81 м/с2.

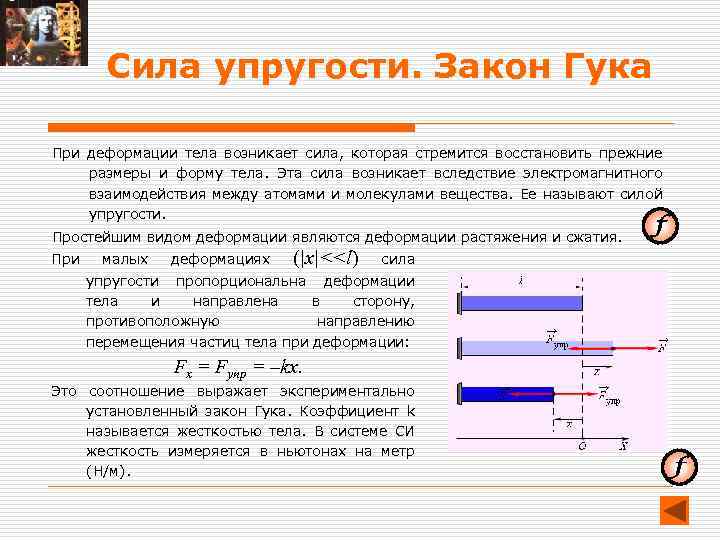Сила упругости. Закон Гука При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости. Простейшим видом деформации являются деформации растяжения и сжатия. При малых деформациях (|x|<

Сила трения Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел. Силами сухого трения называют силы, возникающие при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Они всегда направлены по касательной к соприкасающимся поверхностям. Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону.

Сила трения покоя не может превышать некоторого максимального значения (Fтр)max. Если внешняя сила больше (Fтр)max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Опыт показывает, что сила трения скольжения пропорциональна силе нормального давления тела на опору, а следовательно, и силе реакции опоры Fтр = (Fтр)max = μN Коэффициент пропорциональности μ называют коэффициентом трения скольжения. Коэффициент трения – величина безразмерная. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости

Импульс тела. Закон сохранения импульса Пусть на тело в течение некоторого малого промежутка времени действовала сила. Из второго закона Ньютона следует: Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения), обозначается [кг·м/с]. Физическая величина, равная произведению силы на время ее действия, называется импульсом силы, обозначается [Н·с]. В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы. Именно в таком общем виде сформулировал второй закон сам Ньютон.

Импульс тела. Закон сохранения импульса При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса.

Работа силы. Мощность Если под действием силы тело перемещается, то сила совершает механическую работу: Работа является скалярной величиной. А > 0 Дж, если 0° ≤ α < 90°; А < 0 Дж, если 90° < α ≤ 180°; А = 0 Дж, если α = 90°. Работа силы, совершаемая в единицу времени, называется мощностью. В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Кинетическая энергия Если тело некоторой массы двигалось под действием приложенных сил, и его скорость изменилась, то силы совершили определенную работу. Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы. Это утверждение называют теоремой о кинетической энергии. Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела: Кинетическая энергия – это энергия движения.

Потенциальная энергия – это энергия взаимодействия тел, она определяется взаимным положением тел или частей одного и того же тела. Например, взаимодействие тела, поднятого над поверхностью Земли и Землей, частей деформированной пружины. Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными Работа консервативных сил на замкнутой траектории равна нулю. Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести Работа этой силы зависит только от вертикального перемещения тела. Если тело переместилось из точки, расположенной на высоте h 1, в точку, расположенную на высоте h 2 от начала координатной оси OY, то сила тяжести совершила работу: A = –mg (h 2 – h 1) = –(mgh 2 – mgh 1) Eр = mgh – потенциальная энергия тела в поле силы тяжести. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком: A = –(Eр2 – Eр1). Потенциальная энергия тела на расстоянии r от центра Земли:

Потенциальная энергия Деформированная пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией упруго деформированного тела называют величину: Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x 1, тогда при переходе в новое состояние с удлинением x 2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:

Закон сохранения механической энергии Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: A = –(Eр2 – Eр1). По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел: А = Ek 2 - Ek 1. Следовательно Ek 1 + Ep 1 = Ek 2 + Ep 2. Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

Простые механизмы. КПД механизма Простой механизм – устройство, служащие для преобразования силы. К простым механизмам относятся наклонная плоскость и рычаг. Наклонная плоскость – это плоская поверхность, установленная под углом, отличным от прямого, к горизонтальной поверхности, она позволяет преодолевать значительное сопротивление, прилагая сравнительно малую силу на большем расстоянии, чем то, на которое нужно поднять груз. Рычаг – твёрдое тело, вращающееся вокруг точки опоры. Рычаг используется для получения большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие. Рычаг находится в равновесии, если разность моментов сил, приложенных к нему, равна нулю. На практике совершенная работа с помощью механизма всегда несколько больше полезной работы. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма.

Условия равновесия твердого тела Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс. Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. В общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение двух условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов сил.

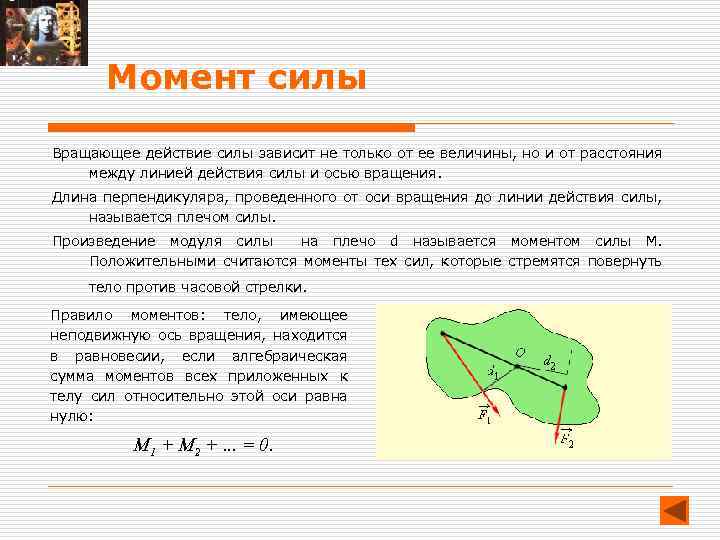Момент силы Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы. Произведение модуля силы на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки. Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю: M 1 + M 2 +. . . = 0.

Давление. Атмосферное давление — гидростатическое давление атмосферы на все находящиеся в ней предметы и Земную поверхность. Атмосферное давление создаётся гравитационным притяжением воздуха к Земле. В 1643 Эванджелиста Торричелли показал, что воздух имеет вес. Совместно с В. Вивиани, Торричелли провёл первый опыт по измерению атмосферного давления, изобретя трубку Торричелли (первый ртутный барометр), — стеклянную трубку, в которой нет воздуха. В такой трубке ртуть поднимается на высоту около 760 мм. На земной поверхности атмосферное давление изменяется от места к месту и во времени. Нормальным атмосферным давлением называют давление в 760 мм рт. ст. (101 325 Па). Атмосферное давление уменьшается по мере увеличения высоты, поскольку оно создаётся лишь вышележащим слоем атмосферы. На картах давление показывается с помощью изобар — линий, соединяющих точки с одинаковым приземным атмосферным давлением, обязательно приведенным к уровню моря. Атмосферное давление измеряется барометром.

Закон Паскаля. Закон Архимеда На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких сил вводится давление – отношение модуля силы действующей перпендикулярно поверхности, к площади этой поверхности: 1 атм = 101325 Па = 760 мм рт. ст. Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует – закон Паскаля. На грани погруженной в жидкость призмы, плотность материала которой равна плотности жидкости должно оказываться одинаковое давление: p 1 = p 2 = p 3 = p.

Закон Паскаля. Закон Архимеда Гидростатическое давление на дно и боковые стенки цилиндрического сосуда высоты h равно: Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой можно создавать в жидкости дополнительное давление: p 0 = F / S. Таким образом, полное давление глубине h можно записать в виде: в жидкости на p = p 0 + ρgh. Если поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению: p 0 = pатм.

Закон Паскаля. Закон Архимеда Из-за разности давлений в жидкости выталкивающая или архимедова сила. на разных уровнях возникает В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S. Разность давлений на нижнюю и верхнюю грани: Δp = p 2 – p 1 = ρgh. Поэтому выталкивающая сила будет направлена вверх, и ее модуль равен FА = F 2 – F 1 = SΔp = ρg. Sh = ρg. V, V – объем вытесненной телом жидкости, ρV – масса вытесненной жидкости. Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.

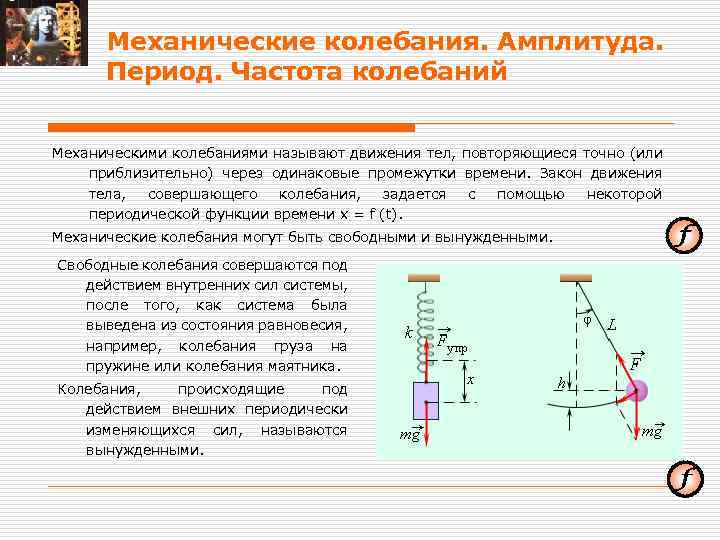Механические колебания. Амплитуда. Период. Частота колебаний Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t). Механические колебания могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия, например, колебания груза на пружине или колебания маятника. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Механические колебания. Амплитуда. Период. Частота колебаний Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением x = xm cos (ωt + φ0). Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, т. е. количество колебаний за 2π с, t – время. Величина, φ = ωt + φ0 – фаза гармонического процесса, φ = φ0, φ0 - начальная фаза. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Количество колебаний за единицу времени называют частотой колебаний:

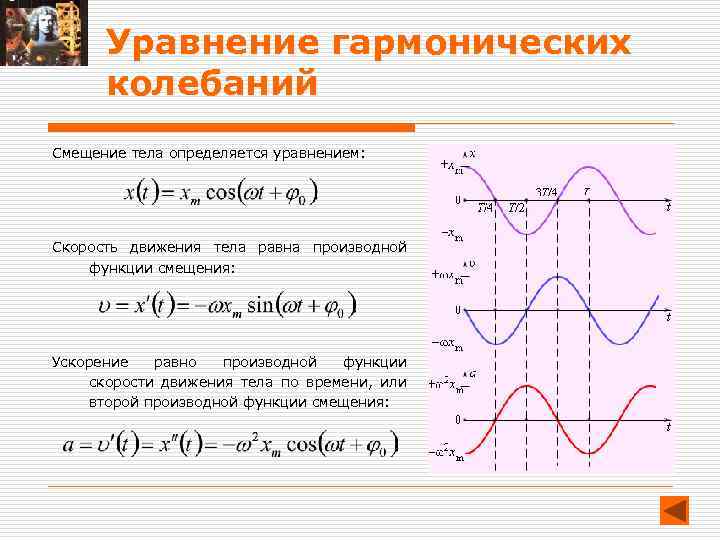Уравнение гармонических колебаний Смещение тела определяется уравнением: Скорость движения тела равна производной функции смещения: Ускорение равно производной функции скорости движения тела по времени, или второй производной функции смещения:

Свободные колебания. Превращения энергии при механических колебаниях Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению: F (t) = ma (t) = –m ω2 x (t). Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kx. Силы, удовлетворяющие этому условию, называются квазиупругими. Груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.

Свободные колебания. Превращения энергии при механических колебаниях Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона: Частота ω0 называется собственной частотой колебательной системы. Период T гармонических колебаний груза на пружине равен: По аналогии с грузом на пружине для груза на нити можно получить:

Свободные колебания. Превращения энергии при механических колебаниях При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины. Для математического маятника – это энергия в поле тяготения Земли. Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д. Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Свободные колебания. Превращения энергии при механических колебаниях Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. Для груза на пружине: Для малых колебаний математического маятника:

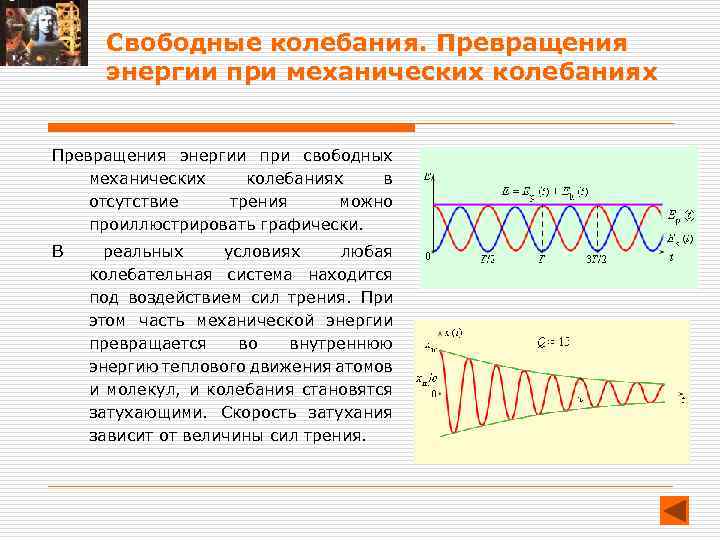Свободные колебания. Превращения энергии при механических колебаниях Превращения энергии при свободных механических колебаниях в отсутствие трения можно проиллюстрировать графически. В реальных условиях любая колебательная система находится под воздействием сил трения. При этом часть механической энергии превращается во внутреннюю энергию теплового движения атомов и молекул, и колебания становятся затухающими. Скорость затухания зависит от величины сил трения.

Вынужденные колебания. Резонанс Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения. Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте. После начала воздействия внешней силы на колебательную систему необходимо некоторое время для установления вынужденных колебаний. В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте внешней вынуждающей силы.

Вынужденные колебания. Резонанс Пусть внешняя сила приложена к свободному концу пружины и заставляет его перемещаться по закону y = ym cos ωt. где ym – амплитуда колебаний, ω – круговая частота. Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно: Δl = x – ym cos ωt. Второй закон Ньютона для тела массой m принимает вид : ma = –k(x – y) = –kx + kym cos ωt. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – вынуждающая сила.

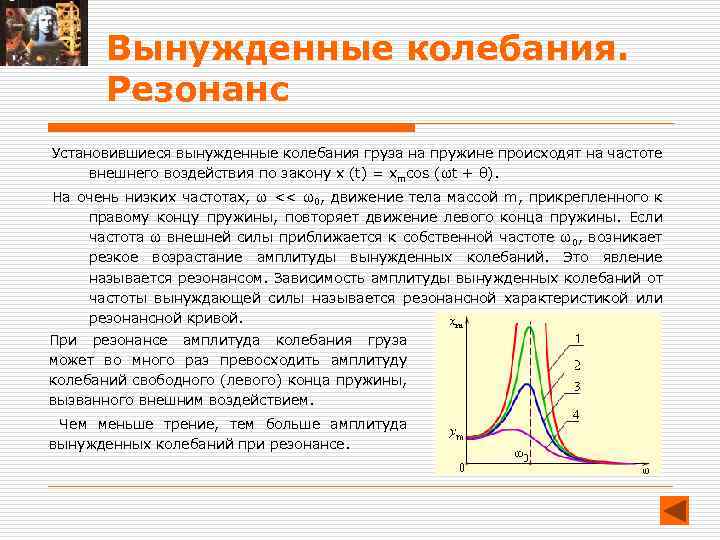Вынужденные колебания. Резонанс Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону x (t) = xmcos (ωt + θ). На очень низких частотах, ω << ω0, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной характеристикой или резонансной кривой. При резонансе амплитуда колебания груза может во много раз превосходить амплитуду колебаний свободного (левого) конца пружины, вызванного внешним воздействием. Чем меньше трение, тем больше амплитуда вынужденных колебаний при резонансе.

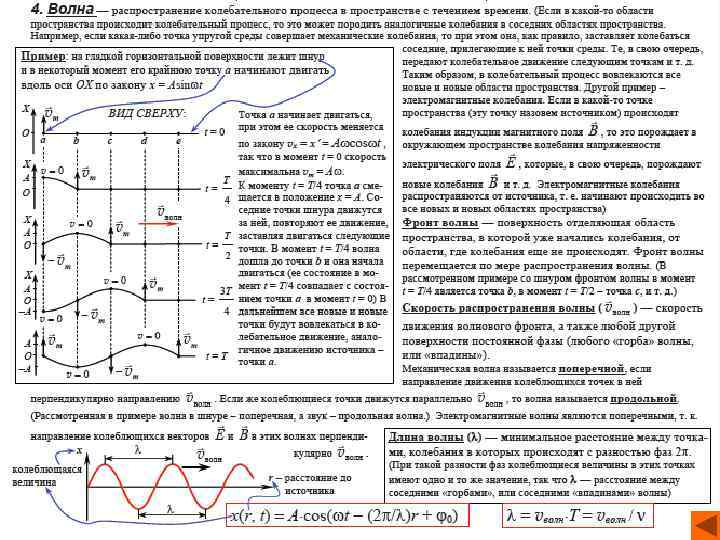
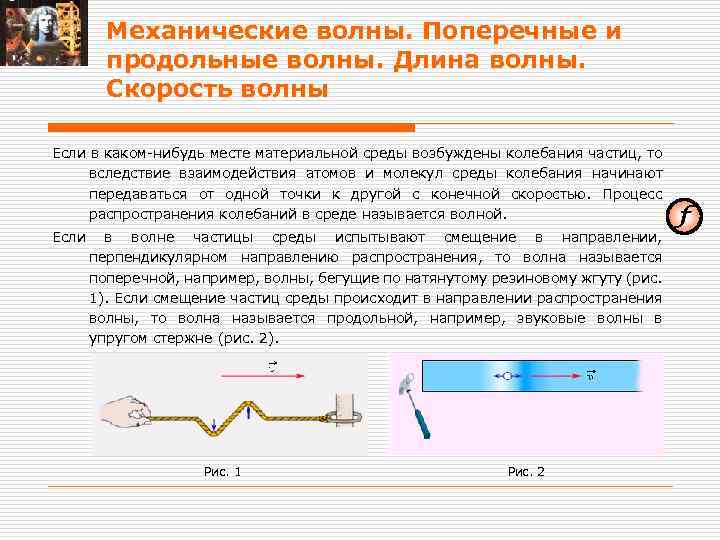Механические волны. Поперечные и продольные волны. Длина волны. Скорость волны Если в каком-нибудь месте материальной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной, например, волны, бегущие по натянутому резиновому жгуту (рис. 1). Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной, например, звуковые волны в упругом стержне (рис. 2). Рис. 1 Рис. 2

Механические волны. Поперечные и продольные волны. Длина волны. Скорость волны При распространения волны переноса вещества не происходит: частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой. Продольные волны могут распространяться в любых средах – твердых, жидких и газообразных. поперечные – только в твердом теле или на поверхности жидкости. Смещение y (x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону: где k –волновое число, ω – круговая частота. Гармонические волны характеризуются амплитудой колебания частиц, частотой, длиной волны и распространяются в однородных средах с некоторой постоянной скоростью.

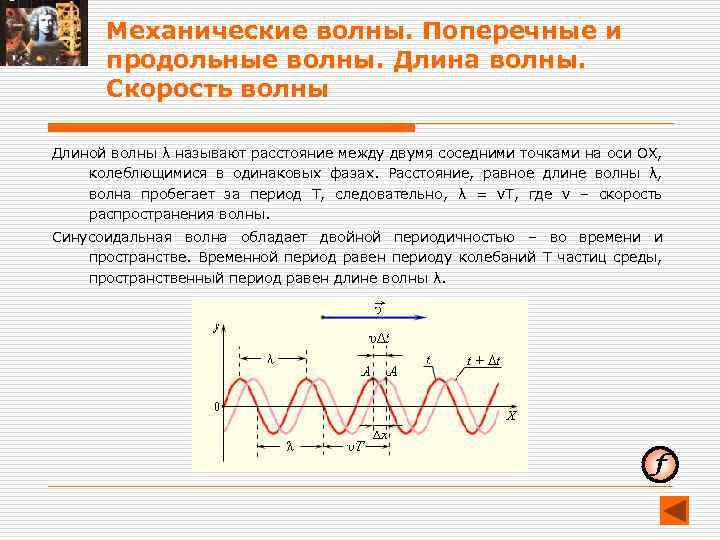Механические волны. Поперечные и продольные волны. Длина волны. Скорость волны Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = v. T, где v – скорость распространения волны. Синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны λ.

Звуковыми волнами или просто звуком принято называть волны, воспринимаемые человеческим ухом. Диапазон звуковых частот лежит в пределах приблизительно от 20 Гц до 20 к. Гц. Волны с частотой менее 20 Гц называются инфразвуком, а с частотой более 20 к. Гц – ультразвуком. Волны звукового диапазона могут распространяться в газе, в жидкости и в твердом теле. Изучением звуковых явлений занимается раздел физики, который называют акустикой. При распространении звука в газе атомы и молекулы колеблются вдоль направления распространения волны. Это приводит к изменениям локальной плотности и давления. В простых гармонических звуковых волнах, распространяющихся вдоль оси OX, изменение давления p (x, t) зависит от координаты x и времени t по закону p (x, t) = p 0 cos (ωt ± kx). Два знака в аргументе распространения волны. косинуса соответствуют двум направлениям Скорость звука сильно зависит от свойств газа. Чем легче газ, тем больше скорость звука в этом газе. В жидкостях и твердых телах скорость звуковых волн еще больше.

Звук При восприятии различных звуков человеческое ухо оценивает их прежде всего по уровню громкости, зависящей от потока энергии или интенсивности звуковой волны. Воздействие звуковой волны на барабанную перепонку зависит от звукового давления, т. е. амплитуды p 0 колебаний давления в волне. Порог слышимости соответствует значению p 0 порядка 10– 10 атм, т. е. 10– 5 Па. При таком слабом звуке молекулы воздуха колеблются в звуковой волне с амплитудой всего лишь 10– 7 см! Болевой порог соответствует значению p 0 порядка 10– 4 атм или 10 Па. Еще одной характеристикой звуковых волн является высота звука. Колебания в гармонической звуковой волне воспринимаются человеческим ухом как музыкальный тон. Колебания высокой частоты воспринимаются как звуки высокого тона, колебания низкой частоты – как звуки низкого тона. Звуки, издаваемые музыкальными инструментами, а также звуки человеческого голоса могут сильно различаться по высоте тона и по диапазону частот. Так, например, диапазон наиболее низкого мужского голоса – баса – простирается приблизительно от 80 до 400 Гц, а диапазон высокого женского голоса – сопрано – от 250 до 1050 Гц.

I. Кинематика

Кинематика

Кинематика

II. Динамика

II. Динамика

II. Динамика

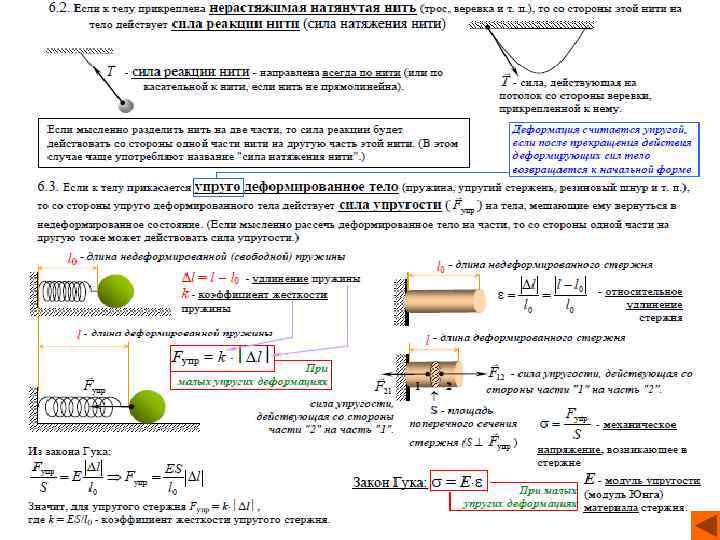
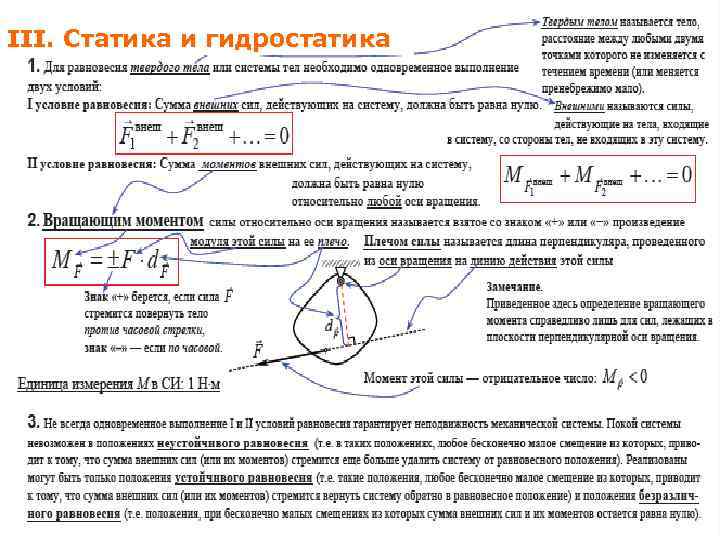III. Статика и гидростатика

III. Статика и гидростатика

III. Статика и гидростатика

III. Статика и гидростатика

III. Статика и гидростатика

III. Статика и гидростатика

V. Колебания и волны

V. Колебания и волны

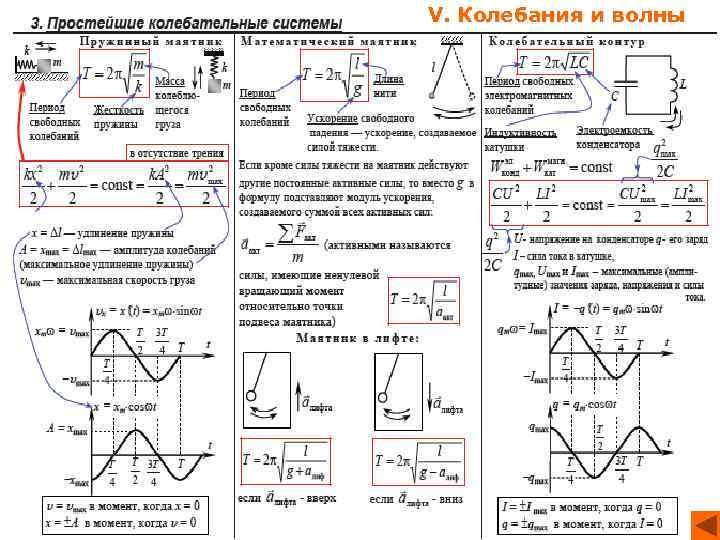V. Колебания и волны