Скачать презентацию Механическое действие взрыва 1 Детонация ВВ При воздействии
Действие взрыва(лекция).ppt
- Количество слайдов: 16
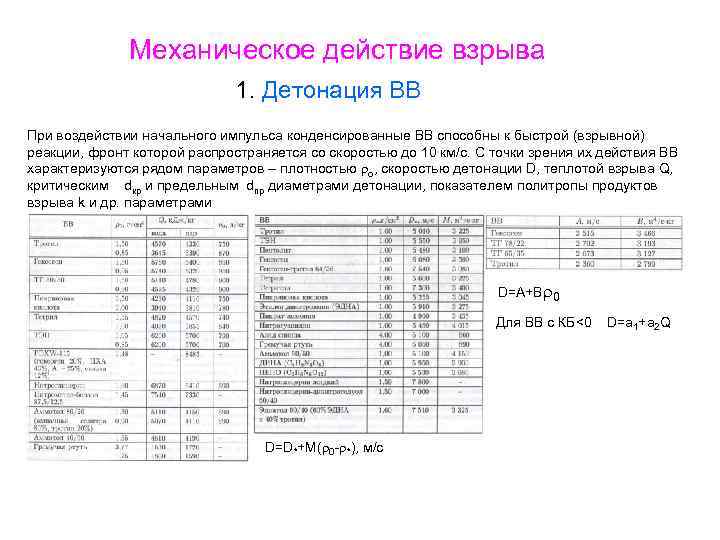Механическое действие взрыва 1. Детонация ВВ При воздействии начального импульса конденсированные ВВ способны к быстрой (взрывной) реакции, фронт которой распространяется со скоростью до 10 км/с. С точки зрения их действия ВВ характеризуются рядом параметров – плотностью o, скоростью детонации D, теплотой взрыва Q, критическим dкр и предельным dпр диаметрами детонации, показателем политропы продуктов взрыва k и др. параметрами D=A+B 0 Для ВВ с КБ<0 D=D*+M( 0 - *), м/с D=a 1+a 2 Q
Элементы гидродинамической теории детонации • Законы сохранения на фронте ДВ • массы 0 D= v= j (1) V=1/ • импульса p 0+ 0 D 2= p+ v 2 (2) • энергии w 0+Q+ D 2/2=w+ v 2/2 (3) • • V 0=1/ 0 D=j. V 0 v=j. V e 0+p 0/ 0+Q+D 2/2=e+ p/ +v 2/2 j 2=(p-p 0)/(V 0 -V) D-v=u=[(p-p 0)(V 0 -V)]1/2 p=p 0+j 2(V 0 -V) прямая Михельсона w=w-w 0=Q+(j 2/2)(V 02 -V 2)=Q+(p-p 0)(V 0+V)/2 w= e+ p/ e=e-e 0=Q+(p+p 0)(V 0 -V)/2 адиабата ПВ Политропный газ: p. Vk=const, e=p. V/(k-1), c 2=kp. V Адиабата ПВ p/p 0=[ -V/V 0+2 k. Q/c 02]/( V/V 0 -1) асимптотa: V=V 0/ Адиабата Гюгонио: p/p 0=[ -V/V 0]/( V/V 0 -1) Структура ДВ: =(k+1)/(k-1)
Детонация Жуге • • • Условие Чепмена-Жуге: tg =(p-p 0)/(V-V 0)=(dp/d. V)H= -kp/V = -j 2 Cильные волны p>>p 0: D=(2(k 2 -1)Q)1/2 P= 0 D 2/(k+1) V=V 0 k/(k+1) = 0(k+1)/k u=D-v=D/(k+1) c=v=Dk/(k+1) C VT=u 2/k(k+1) D=u+c • • • Кубическое уравнение состояния • Изэнтропический разлет продуктов детонации в пустоту P=A 3 =A 1 c 3 (k=3): =4 0/3, P= 0 D 2/4, u=D/4, c=3 D/4 Особое решение уравнений г/динамики x=(u+c)t+f(v) u= c + const Детонация начинается при t=0 в точке х=0, след. f(v)=0 Из усл. на фронте силь. ДВ находим cоnst= D/4 -3 D/4= -D/2, след. u=x/2 t-D/4 c=x/2 t+D/4 Макс. скорость разлета ПД в голове ВР (с=0 и x= -Dt/2) um= -D/2
2. Взаимодействия ДВ с преградами • 1. • • 2. Жесткая преграда C> 0 D. В ПВ и преграде возникают УВ Ударная адиабата конденсированных сред U=C+bu u=u-ux=[(Px-P)(V-Vx)]1/2 z=Px/P P= Uu= u(C+bu) Vx/V=[(k+1)P+(k-1)Px]/[(k-1)P+(k+1)Px] ux /u=1 -[2 k(z-1)2/(k-1+(k+1)z)]1/2 z= ux(C+bux)/P Отсюда находим ux и затем Рх Абсолютно жесткая преграда ux=0 z=1+((k+1)/4 k)[1+(1+(4 k/(k+1))2]1/2 =2. 39 при k=3 3. Мягкая преграда C< 0 D. В преграде возникает УВ, в ПВ – волна разрежения u=ux-u=Px Р d. P/ c=u[(2 k/(k-1))(1 -z(k-1)/2 k] z= ux(C+bux)/P Отсюда находим ux и затем Рх Истечение ПД в вакуум (воздух) Рх=0 ux=(3 k-1)D/(k 2 -1)=D при k=3 =4. 9 D при k=1. 25. Обычно ux 2 D
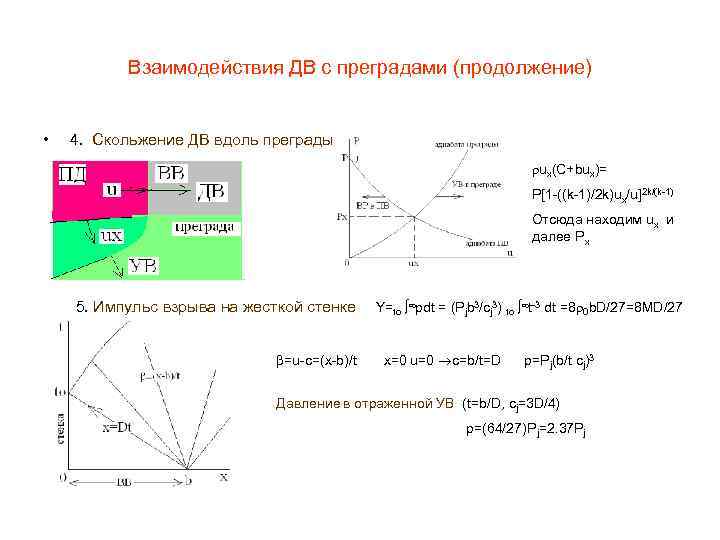Взаимодействия ДВ с преградами (продолжение) • 4. Скольжение ДВ вдоль преграды ux(C+bux)= P[1 -((k-1)/2 k)ux/u]2 k/(k-1) Отсюда находим ux и далее Рх 5. Импульс взрыва на жесткой стенке =u-c=(x-b)/t Y=to pdt = (Pjb 3/cj 3) to t-3 dt =8 0 b. D/27=8 MD/27 x=0 u=0 c=b/t=D p=Pj(b/t cj)3 Давление в отраженной УВ (t=b/D, cj=3 D/4) p=(64/27)P j=2. 37 Pj
Метание тел взрывом • На торце заряда ВВ (x=b) находится тонкая (несжимаемая) пластина массой m (на единицу площади). При взаимодействии ДВ с пластиной последняя получает импульс и приходит в движение со скоростью u(x, t), описываемой уравнением mdu/dt=p, p=ac 3 (k=3) =u+c=x/t –u mdu/dt=a(x/t –u)3 md 2 x/dt 2=a(x/t –dx/dt) Предельная скорость пластины (g=m/M) u/D=(27/16 g)[1+16 g/27 –(1+32 g/27)1/2] g 0 (тяжелая пластина, мало ВВ) u/D 0 g (легкая пластина, много ВВ) u/D 1 (как при разлете ПВ в пустоту) Доля энергии ВВ, получаемая пластиной, или КПД заряда ВВ Калорийность ВВ есть E=MD 2/2(k 2 -1)=MD 2/16 (k=3); энергия пластины e=mu 2/2 КПД заряда s=e/E=(8/g)(u/D)2=(729/32 g 3)[1+16 g/27 -(1+32 g/27)1/2]2 Функция s(g) имеет максимум, равный sm=(16/27)2 0. 35 при g=81/32 2. 53 (пластина тяжелее ВВ). При этом u/D=1/3.
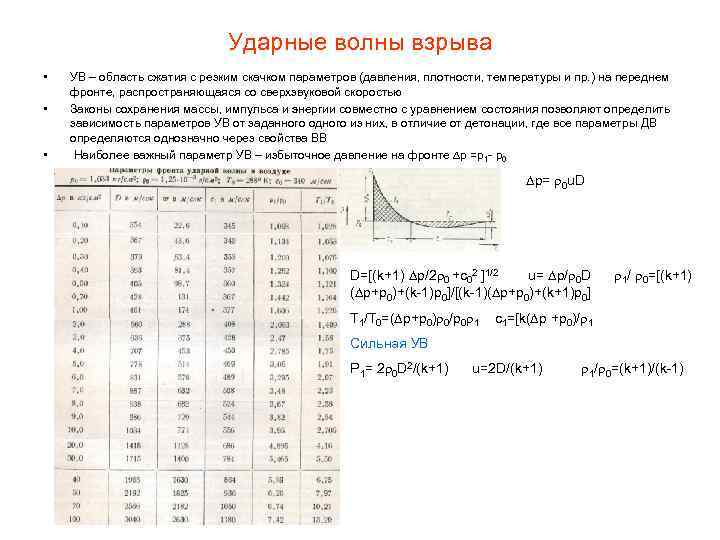Ударные волны взрыва • • • УВ – область сжатия с резким скачком параметров (давления, плотности, температуры и пр. ) на переднем фронте, распространяющаяся со сверхзвуковой скоростью Законы сохранения массы, импульса и энергии совместно с уравнением состояния позволяют определить зависимость параметров УВ от заданного одного из них, в отличие от детонации, где все параметры ДВ определяются однозначно через свойства ВВ Наиболее важный параметр УВ – избыточное давление на фронте р =р1 - р0 р= 0 u. D D=[(k+1) р/2 0 +c 02 ]1/2 u= р/ 0 D ( р+p 0)+(k-1)p 0]/[(k-1)( р+p 0)+(k+1)p 0] T 1/T 0=( р+p 0) 0/p 0 1 1/ 0=[(k+1) c 1=[k( р +p 0)/ 1 Сильная УВ P 1= 2 0 D 2/(k+1) u=2 D/(k+1) 1/ 0=(k+1)/(k-1)
Cильный (точечный) взрыв в однородной атмосфере В небольшом объеме газа радиусом r 0 и плотности 0 в течение короткого промежутка времени ( «мгновенно» ) выделяется большая энергия Е. От места энерговыделения по газу распространяется УВ. Рассмотрим стадию процесса, когда УВ уходит на расстояния R>>r 0, но при этом давление на фронте УВ р1>>p 0, т. е. волна еще остается достаточно сильной. Единственная безразмерная комбинация, содержащая длину, время, энергию и плотность, есть j= r( 0/Et 2)1/5. Фронту УВ соответствует определенное значение независимой переменной j 0. Поэтому закон движения фронта волны R(t) описывается формулой R= j 0(Et 2/ 0)1/5. Cкорость распространения УВ равна D=d. R/dt=2 R/5 t=(2 j 0/5)(E/ 0 t 3)1/5=(2/5)j 05/2(E/ 0)1/2 R-3/2. Используя формулы для параметров на фронте сильной УВ, найдем закон уменьшения давления с течением времени p 1=(8 0 j 02/(25(k+1))(E/ 0 t 3)2/5= (8 0 j 05/(25(k+1))(E/ 0 R 3) или p 1 E/R 3. Выделенная красным цветом формула демонстрирует закон подобия для перехода от одних энергий взрыва к другим. Давление на фронте имеет заданную величину на расстояниях, пропорциональных Е 1/3. • • Закон подобия при взрыве Наиболее просто закон подобия формулируется для взрыва зарядов сферической формы. Поскольку энергия взрыва Е=MQ, то заряд данного ВВ массой М 1 создает давление р на расстоянии R 1, а заряд массой М 2 создаeт то же давление на расстоянии R 2; при этом R 1/R 2=(M 1/M 2)1/3, т. е. R M 1/3. Поэтому удобно ввести т. н. приведенный радиус по формуле R 0=R/M 1/3. Обычно R измеряется в м, а М – в кг. Тогда согласно закону подобия р=f(R 0). Вид функции f определяется из опыта. Замечания: 1) При взрывах зарядов из различных ВВ следует учитывать их калорийность и в R 0 подставлять энергетические эквиваленты зарядов Мэкв=МQ/Qтнт, где М – масса взятого заряда, Q – его калорийность, Qтнт – теплота взрыва ТНТ, принятая в качестве эквивалента (тротиловый эквивалент). Округленно Qтнт=1000 ккал/кг = 4. 2 МДж/кг. 2) 2) Тротиловый эквивалент позволяет сравнивать между собой взрывы различной природы – электрические, атомные, вулканические и пр. Для этого достаточно знать выделившуюся в каждом случае энергию и подставлять в R 0 массу заряда ТНТ, эквивалентную по энергии данному взрыву.
Разрушающее действие взрыва Для оценки разрушающего действия взрыва (РДВ) необходимо знать характер УВнагрузки и свойства сооружения, на которое действует нагрузка. Если t+ - время действия фазы сжатия УВ и Т - период собственных колебаний элементов сооружения, то при t+>>T РДВ определяется величиной избыточного давления р=р1 -р0 (статическое действие УВ). При t+<
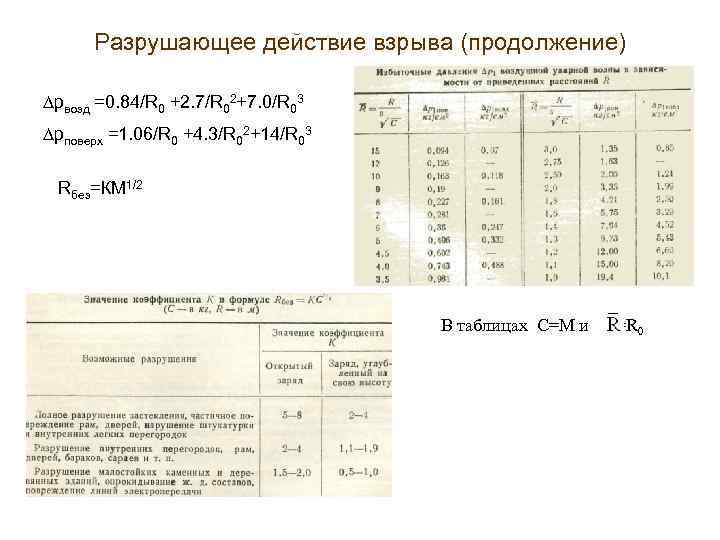Разрушающее действие взрыва (продолжение) рвозд =0. 84/R 0 +2. 7/R 02+7. 0/R 03 рповерх =1. 06/R 0 +4. 3/R 02+14/R 03 Rбез=КМ 1/2 В таблицах С=М и =R 0
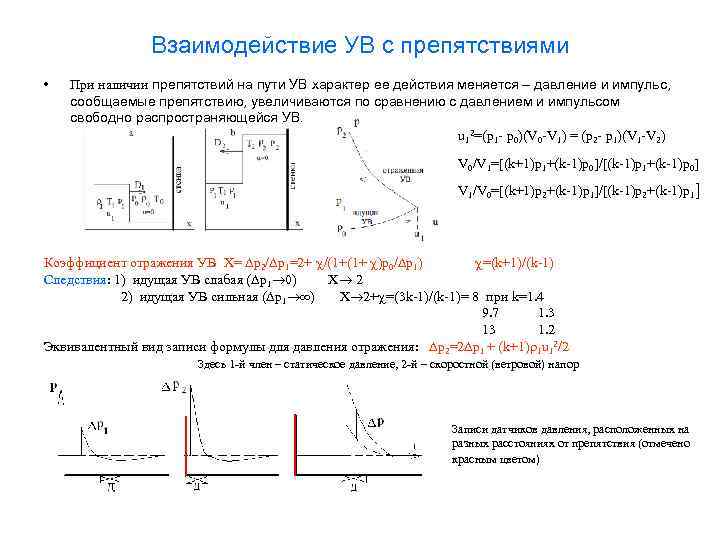Взаимодействие УВ с препятствиями • При наличии препятствий на пути УВ характер ее действия меняется – давление и импульс, сообщаемые препятствию, увеличиваются по сравнению с давлением и импульсом свободно распространяющейся УВ. u 12=(p 1 - p 0)(V 0 -V 1) = (p 2 - p 1)(V 1 -V 2) V 0/V 1=[(k+1)p 1+(k-1)p 0]/[(k-1)p 1+(k-1)p 0] V 1/V 0=[(k+1)p 2+(k-1)p 1]/[(k-1)p 2+(k-1)p 1] Коэффициент отражения УВ Х= p 2/ p 1=2+ /(1+(1+ )p 0/ p 1) =(k+1)/(k-1) Cледствия: 1) идущая УВ слабая ( p 1 0) Х 2 2) идущая УВ сильная ( p 1 ) Х 2+ =(3 k-1)/(k-1)= 8 при k=1. 4 9. 7 1. 3 13 1. 2 Эквивалентный вид записи формулы для давления отражения: p 2=2 p 1 + (k+1) 1 u 12/2 Здесь 1 -й член – статическое давление, 2 -й – скоростной (ветровой) напор Записи датчиков давления, расположенных на разных расстояниях от препятствия (отмечено красным цветом)
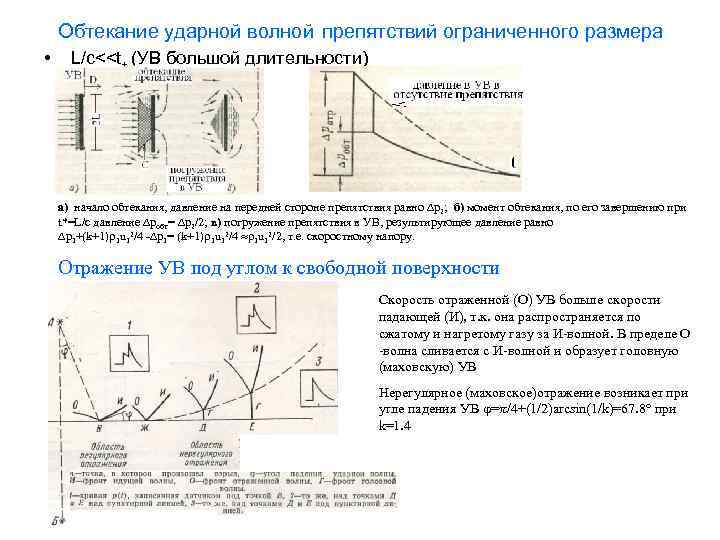Обтекание ударной волной препятствий ограниченного размера • L/с<
Ударные волны в грунте и нагрузки на сооружения Зоны разрушений грунта при подземном (камуфлетном) взрыве заряда ВВ 1. Зона вытеснения – область, из которой ПВ высокого давления вытеснили грунт, образовав сферическую полость ( «котел» ) 2. Зона раздавливания – область, пронизанная поверхностями скольжения, в которой грунт интенсивно раздроблен в результате воздействия УВ 3. Зона разрыва – область, в которой ослабевшая УВ не в состоянии раздавить породу сжатием. Однако среда получает значительное радиальное смещение (от центра взрыва), вследствие которого в среде возникают растягивающие усилия, приводящие к появлению радиальных трещин. Последующая разгрузка обусловливает образование кольцевых тангенциальных трещин 4. Зона сотрясения – область, где сильно ослабевшая УВ не способна нарушить связи между частицами грунта и производит более или менее сильное сотрясение, ослабевающее по мере распространения волны Размер каждой зоны оценивается по закону подобия при взрыве Ri*=Ri/M 1/3, откуда Мi=Ki. Ri 3, где Ki=1/(Ri*)3, i=1, 2, 3, 4 Происхождение откола при выходе УВ из твердой среды в воздух t 0 – выход УВ из твердой среды в воздух (вакуум). В этот момент из воздуха в твердую среду проникает ВР той же амплитуды, но с отрицательным профилем давлений. Скорость свободной поверхности равна удвоенной величине скорости потока за падающей УВ t 1, t 2 – промежуточные моменты взаимодействия УВ и ВР. Откол наступает, когда отрицательное напряжение в соответствующем месте тела достигает предела прочности материала на разрыв. От поверхности тела откалывается пластинка материала и отлетает от него с определенной скоростью tk – окончание взаимодействия. Если откол не наступил, то влево распространяется только ВР, по форме идентичная падающей УВ, но с отрицательным профилем давлений
• Множественный откол и оптимальное заложение заряда для рыхления грунта Множественный откол возникает при оптимальных условиях взрывания заряда, когда после первого откола оставшаяся часть УВ отражается от вновь образованной поверхности тела, в результате чего происходит новый откол и т. д. Ориентировочно количество отколов равно max / пр, где max – максимальное напряжение на фронте УВ и пр – предел прочности породы на отрыв. Т. о. при взрыве вблизи свободной поверхности наряду с явлениями, свойственными камуфлетному взрыву, возникает область разрушения, называемая воронкой рыхления. При минимальном заглублении заряда образуется воронка выброса В зоне сотрясения (4) разрушения грунта заканчиваются и начинаются т. н. сейсмические колебания, сопровождающиеся волновыми движениями различной природы как внутри, так и на свободной поверхности грунта. Особенную опасность для сооружений представляют волны поперечного сдвига, внешне похожие на волны на поверхности воды, но распространяющиеся с гораздо более высокими скоростями. Они имеют значительную амплитуду смещений, а период их колебаний близок к периоду собственных колебаний зданий и сооружений. Типичная сейсмограмма взрыва показана слева. Расстояния, на которых колебания грунта становятся безопасными для зданий и сооружений, оцениваем по формуле Rсейсм = Rc* M 1/3. 1 – волна сжатия, 2 – продольная волна, 3 – поперечная волна
Действие заряда выброса • Пропорциональность массе заряда имеет место не только для объема расширения грунта (камуфлетный взрыв), но и для объема выброшенной породы - при создании воронки выброса. При расчетах таких зарядов предполагают, что воронка выброса представляет собой конус, в вершине которого находится взрываемый заряд. Пусть r – радиус воронки, w – ее глубина (линия наименьшего сопротивления, ЛНС). Отношение n=r/w называется показателем действия взрыва. Если n=1, имеем воронку нормального выброса, если n>1 – воронку усиленного выброса. Объем нормальной воронки v=( /3)r 2 w w 3. Необходимая масса заряда для создания такой воронки М=Kv=Kw 3 (М в кг, w в м). Поскольку работа ПВ связана с преодолением инерции грунта, величина К (масса заряда, необходимая для выброса единицы объема грунта) для разных грунтов заключена в узких пределах (1 – 2). В среднем для выброса 1 м 3 грунта требуется приблизительно 1 кг ВВ. Заряды усиленного выброса рассчитывают по формуле Борескова М=Kw 3(0. 4+0. 6 n 3) или (при w>20 м) по формуле Покровского М=Кw 7/2(1+n 2)2. По предложению Беляева эти формулы можно записать в объединенном виде М=K(0. 95+0. 05 w)w 3(0. 4+0. 6 n 3). Т. о. при малых w имеем М w 3, а при больших w масса М w 4.
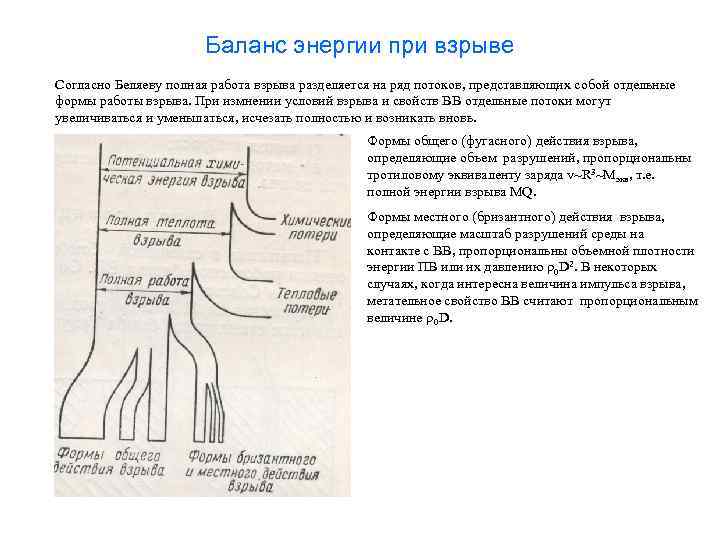Баланс энергии при взрыве Согласно Беляеву полная работа взрыва разделяется на ряд потоков, представляющих собой отдельные формы работы взрыва. При измнении условий взрыва и свойств ВВ отдельные потоки могут увеличиваться и уменьшаться, исчезать полностью и возникать вновь. Формы общего (фугасного) действия взрыва, определяющие объем разрушений, пропорциональны тротиловому эквиваленту заряда v R 3 Mэкв, т. е. полной энергии взрыва МQ. Формы местного (бризантного) действия взрыва, определяющие масштаб разрушений среды на контакте с ВВ, пропорциональны объемной плотности энергии ПВ или их давлению 0 D 2. В некоторых случаях, когда интересна величина импульса взрыва, метательное свойство ВВ считают пропорциональным величине 0 D.