Механические характеристики материалов Испытания по ГОСТ 1497

Механические характеристики материалов

Испытания по ГОСТ 1497 -84 • l 0 • d 0 длинные образцы с отношением l 0/d 0=10 и короткие - l 0/d 0=5

Испытательная разрывная машина

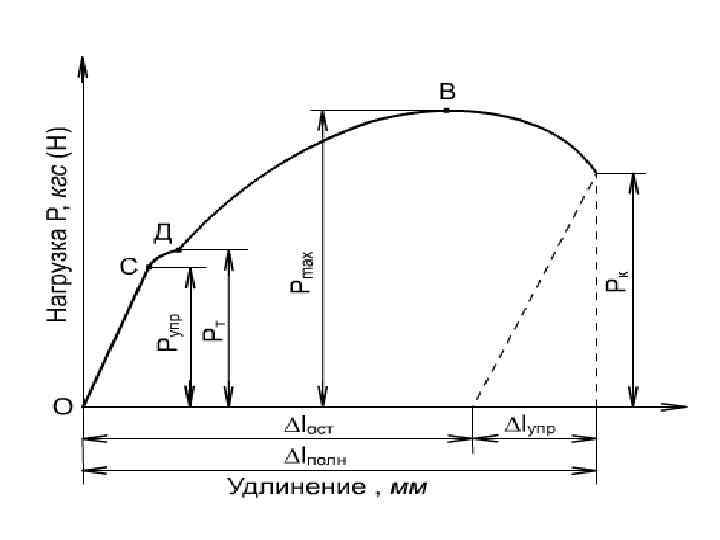
ОС – участок упругих деформаций СД – зона текучести ДВ – зона упрочнения В – точка начала формирования шейки ВК – зона местной текучести

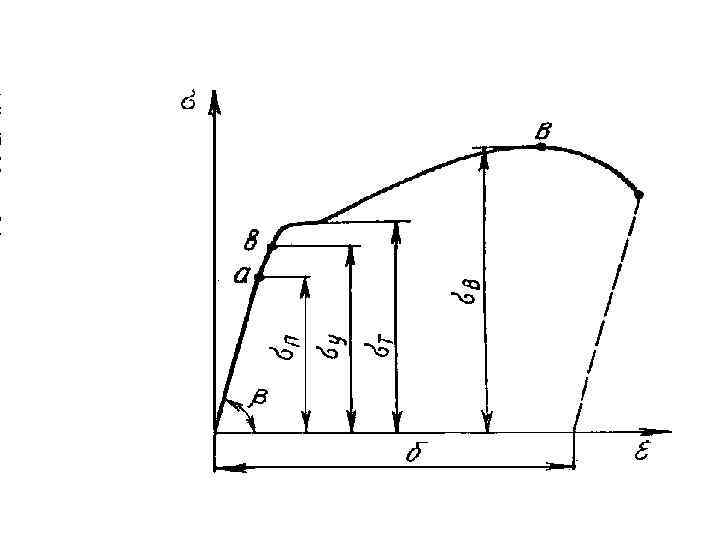
• Пределом пропорциональности пц называется наибольшее напряжение, до которого существует прямо пропорциональная зависимость между нагрузкой и деформацией. • Пределом упругости уп называется максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации.

• Пределом текучести т называется напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки. • Пределом прочности в называется напряжение, соответствующее максимальной нагрузке, достигнутой в ходе испытаний.

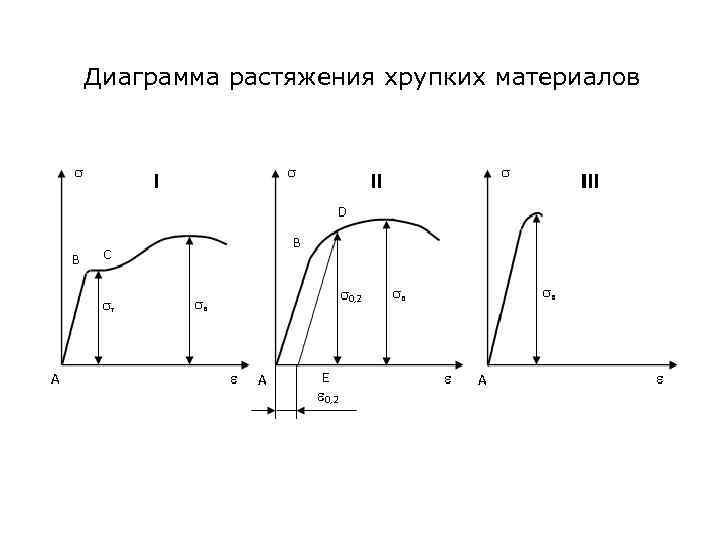Диаграмма растяжения хрупких материалов

• Относительное удлинение после разрыва ( ) – это отношение приращения расчетной длины образца после разрыва к ее первоначальному значению, вычисляемое по формуле: • относительное сужение после разрыва ( ), представляющее собой отношение уменьшения площади поперечного сечения образца в месте разрыва к начальной площади поперечного сечения образца:

Условие прочности: Где [ ] - допускаемое напряжение, т. е. максимальное напряжение при котором нет разрушения и пластических деформаций. [ ]= т/n Где n – коэффициент запаса

Гипотезы прочности

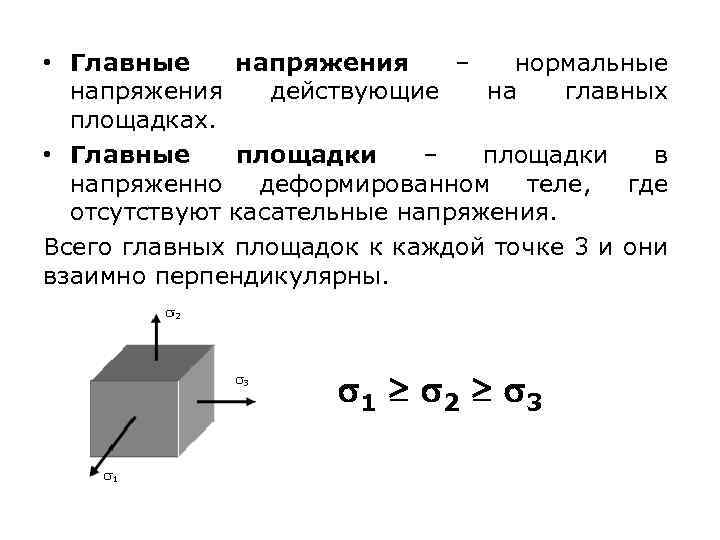• Главные напряжения – нормальные напряжения действующие на главных площадках. • Главные площадки – площадки в напряженно деформированном теле, где отсутствуют касательные напряжения. Всего главных площадок к каждой точке 3 и они взаимно перпендикулярны. 1 2 3

Испытания образцов из определённого материала на простое растяжение или сжатие позволяют без особых трудностей определить значение опасных напряжений: т – предел текучести о = в – временное сопротивление. По опасным напряжениям устанавливают допускаемые при растяжении [ +] или сжатии [ ] напряжения, обеспечивая коэффициент запаса против наступления предельного состояния. Таким образом, условие прочности при одноосном напряженном состоянии принимает вид: 1 [ +], | 3| [ -].

Сложное нагружение

• Первая теория прочности (теория наибольших нормальных напряжений) Согласно этой теории, выдвинутой Галилеем (XVII в. ), преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения. Нарушение прочности в общем случае напряженного состоянии наступает тогда, когда наибольшее нормальное напряжение достигает опасного значения ( 0). Последнее легко устанавливается при простом растяжении на образцах из определённого материала.

1= 0 1 [ ] • Таким образом, первая теория прочности из трех главных напряжений учитывает лишь одно – наибольшее, полагая, что два других не влияют на прочность. • Опытная проверка показывает, что эта теория прочности непригодна для большинства материалов и дает, в общем, удовлетворительные результаты лишь для весьма хрупких материалов.

• Вторая теория прочности (теория наибольших линейных деформаций). Согласно второй теории прочности, предложенной Мариоттом (1682 г. ), принимается в качестве критерия прочности наибольшая по абсолютной величине линейная деформация. По этой теории нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшая линейная деформация max достигает своего опасного значения 0. Последнее определяется при простом растяжении образцов из определённого материала.

max= 0 max [ ] max= 1= [ 1 - ( 2+ 3)]/Е [ ]=[ ]/Е [ 1 - ( 2+ 3)] [ ] Опытная проверка этой теории также показала, что она неприменима для большинства материалов и дает удовлетворительные результаты лишь для хрупкого состояния материала (например, легированный чугун, высокопрочные стали после низкого отпуска). Отметим также, что применение второй теории прочности недопустимо для материалов, не подчиняющихся закону Гука, или за пределами пропорциональности, а также когда наибольшая по абсолютной величине деформация отрицательна.

• Третья теория прочности (теория наибольших касательных напряжений). Согласно третьей теории прочности, предложенной Кулоном (1773 г. ), в качестве критерия прочности принимается величина наибольшего касательного напряжения. По этой теории нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшее касательное напряжение max достигает своего предельного значения 0. Последнее определяется в момент разрушения при простом растяжении.

max= 0 max [ ] max = ( 1 - 3)/2 0 = [ ]/2 1 - 3 = 0 1 - 3 [ ] Третья теория прочности, в общем, хорошо подтверждается опытами для пластичных материалов, одинаково работающих на растяжение и сжатие. Для хрупких материалов она неприменима.

• Четвертая теория прочности (энергетическая теория формоизменения). В качестве критерия прочности принимается количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Согласно этой теории, выдвинутой Губером (1904 г. ), опасное состояние (текучесть) в общем случае напряженного состояния наступает тогда, когда удельная потенциальная энергия формоизменения достигает своего предельного значения. Последнее можно легко определить при простом растяжении в момент текучести.

Uф = (Uф)т Uф [Uф] Uф = [ 12+ 22+ 32 -( 1 2+ 3 2+ 1 3)] (1+ )/3 Е (Uф)т = т2 (1+ )/3 Е Опыты хорошо подтверждают четвертую теорию для пластичных материалов, работающих на растяжение и сжатие. одинаково

• Пятая теория прочности предельных напряженных состояний (теория Мора). Теория прочности предельных напряженных состояний, предложенная Мором (начало ХХв. ), основывается на предположении, что прочность материалов в общем случае напряженного состояния зависит главным образом от величины и знака наибольшего 1 и наименьшего 3 из главных напряжений. Среднее по величине главное напряжение лишь незначительно влияет на прочность.

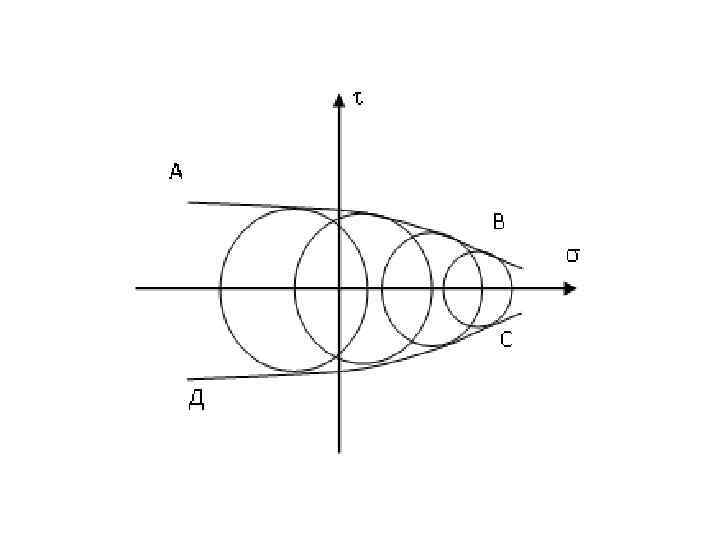
• Опыты показывают, что по мере перехода из области растяжения в область сжатия прочность увеличивается. Это соответствует увеличению диаметров предельных окружностей по мере движения влево. Огибающая АВСД семейства предельных кругов ограничивает область прочности.

Так как первая и вторая теории прочности имеют существенные недостатки, то в настоящее время все более утверждается мнение о нежелательности их применения. Таким образом, для практических расчетов следует рекомендовать: а) третью теорию (или четвертую) – для материалов, одинаково сопротивляющихся растяжению и сжатию; б) теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию.