МЕХАНИЧЕСКИЕ ВОЛНЫ
Волна - процесс распространения колебаний в упругой среде. Классификация волн 1. По физической природе: - механические, - химические (реакция Белоусова-Жаботинского), - электромагнитные (электромагнитное излучение), - гравитационные (гравитационные волны), - спиновые (магноны), - плотности вероятности (ток вероятности) и т. д. 2. По скорости распространения в пространстве: - стоячие, - бегущие.
3. По характеру волны: - колебательные, - уединённые (солитоны). 4. По типу волн: - поперечные, - продольные, - смешанного типа. 5. По способу описания волнового процесса: - линейные, - нелинейные. 6. По свойствам среды: - волны в дискретных структурах, - волны в непрерывных субстанциях. 7. По геометрии: - сферические (пространственные), - одномерные (плоские), - спиральные.
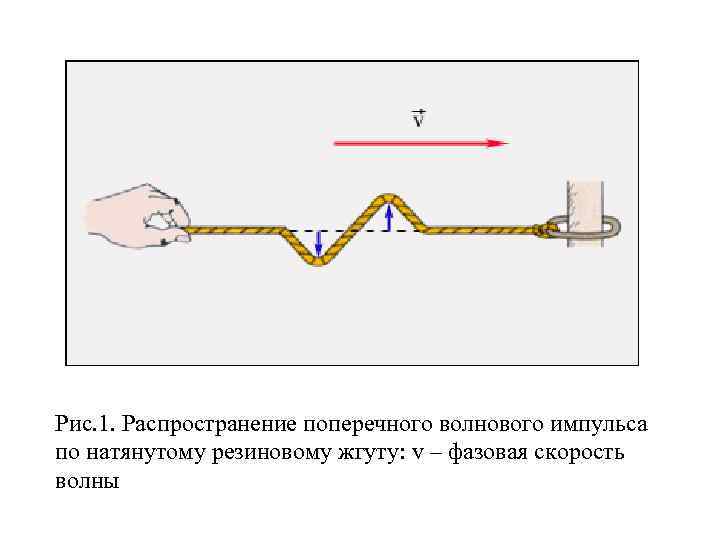
Рис. 1. Распространение поперечного волнового импульса по натянутому резиновому жгуту: v – фазовая скорость волны
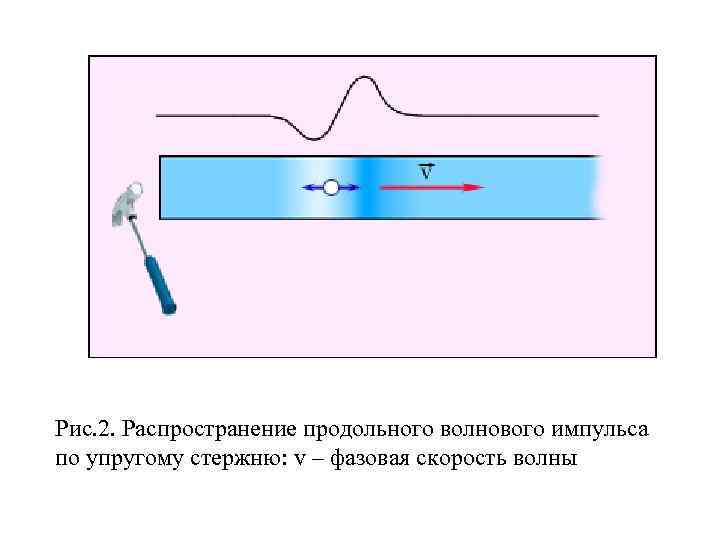
Рис. 2. Распространение продольного волнового импульса по упругому стержню: v – фазовая скорость волны
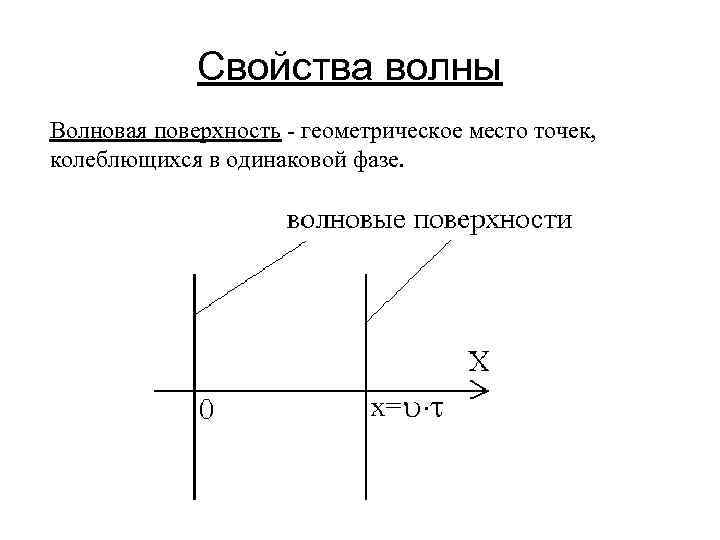
Свойства волны Волновая поверхность - геометрическое место точек, колеблющихся в одинаковой фазе.
Фронт волны - геометрическое место точек, до которых дошли колебания в данный момент времени. Фазовая скорость - скорость с которой перемещается данное значение фазы. Время запаздывания υ- фазовая скорость Волновое число λ- длина волны
Уравнение гармонической волны ξ(x, t) - смещение частиц в точке с координатой x в момент времени t Уравнение плоской незатухающей волны Уравнение плоской затухающей волны (в поглощающей среде)
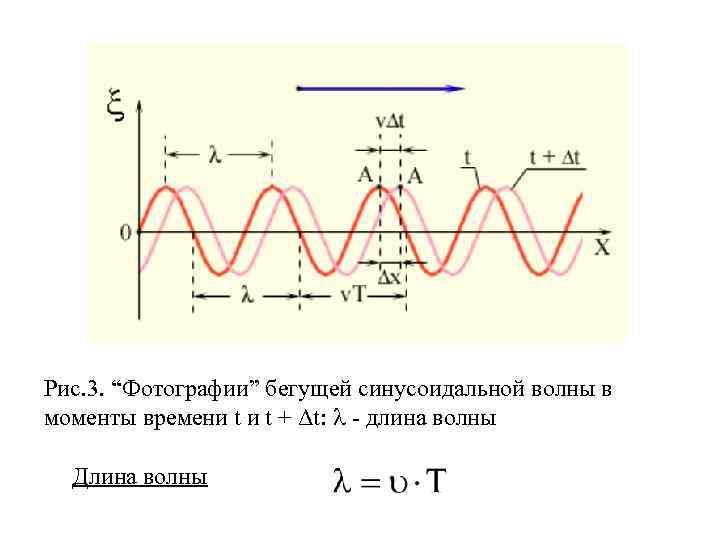
Рис. 3. “Фотографии” бегущей синусоидальной волны в моменты времени t + Δt: - длина волны Длина волны
Уравнение сферической волны в непоглощающей среде: Уравнение сферической волны в поглощающей среде:
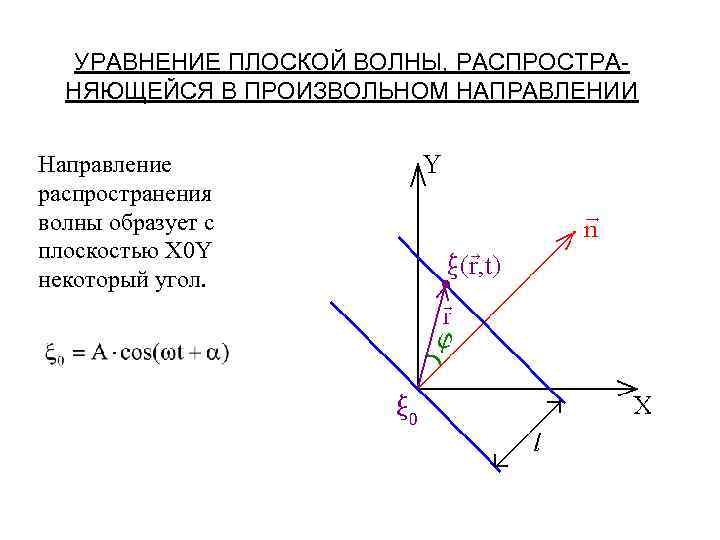
УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ В ПРОИЗВОЛЬНОМ НАПРАВЛЕНИИ Направление распространения волны образует с плоскостью X 0 Y некоторый угол.
Для произвольной точки волновой поверхности: Волновой вектор
Уравнение плоской незатухающей волны Уравнение плоской затухающей волны
Перепишем через координаты уравнение:
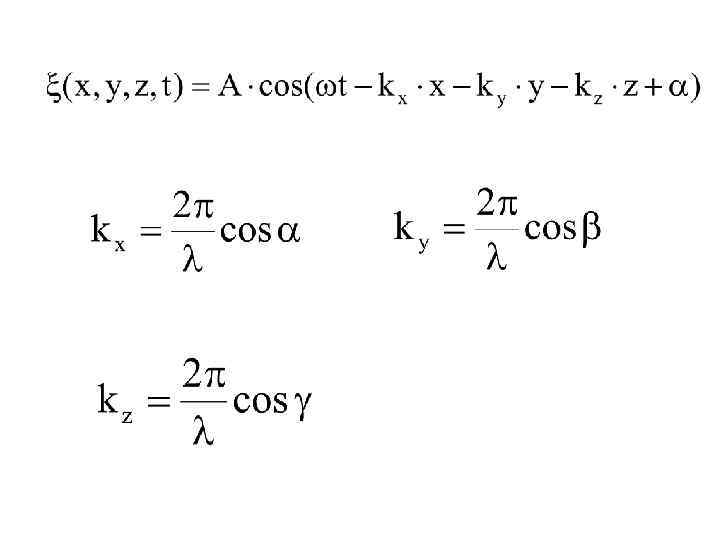
ВОЛНОВОЕ УРАВНЕНИЕ Уравнение волны является решением волнового уравнения. Получим волновое уравнение на примере плоской волны. Вторая производная по времени ¶ 2 x ¶t 2 = ¶ ¶t r r w (- A Ч sin( w t - k Чr + a ) Ч ) = r r = - w 2 A cos( w t - k Чr + a ) = - w 2 x
Вторые производные по координатам
Частный случай. Для плоской волны, распространяющейся в направлении х:
Фазовая скорость продольной волны Е - модуль Юнга Фазовая скорость поперечной волны G - модуль сдвига
ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ Рассмотрим плоскую волну, распространяющуюся в направлении х: Волна переносит энергию от источника колебаний в различные точки среды.
Плотность энергии: Средняя плотность энергии: ρ - плотность среды Поток энергии через заданную поверхность (скалярная величина):
Плотность потока энергии через площадку S┴ (векторная величина): Поток энергии через площадку S┴ Вектор скорости переноса энергии (вектор Умова). Среднее по времени значение вектора Умова:
Интенсивность волны
Скачать презентацию МЕХАНИЧЕСКИЕ ВОЛНЫ Волна — процесс распространения колебаний
МЕХАНИЧЕСКИЕ ВОЛНЫ.ppt