3 Механическая энергия.pptx
- Количество слайдов: 66

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Движение без ускорения (т. е. прямолинейное и равномерное) может происходить как без действия, так и при действии на тело сил. В последнем случае сумма сил, действующих на тело, равна нулю. Между этими двумя видами движений без ускорения имеется существенное различие. В первом случае движение не сопровождается работой, для осуществления второго типа движения нужно затратить работу. Работает мотор, движущий равномерно и прямолинейно автомашину.
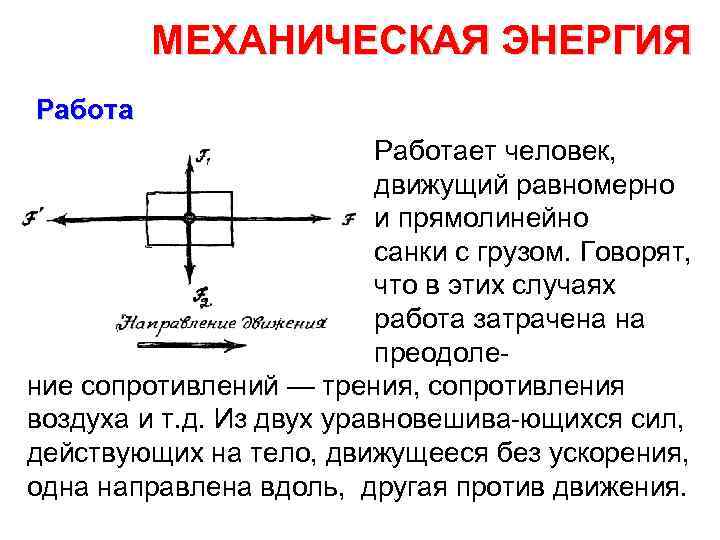
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работает человек, движущий равномерно и прямолинейно санки с грузом. Говорят, что в этих случаях работа затрачена на преодоле ние сопротивлений — трения, сопротивления воздуха и т. д. Из двух уравновешива ющихся сил, действующих на тело, движущееся без ускорения, одна направлена вдоль, другая против движения.
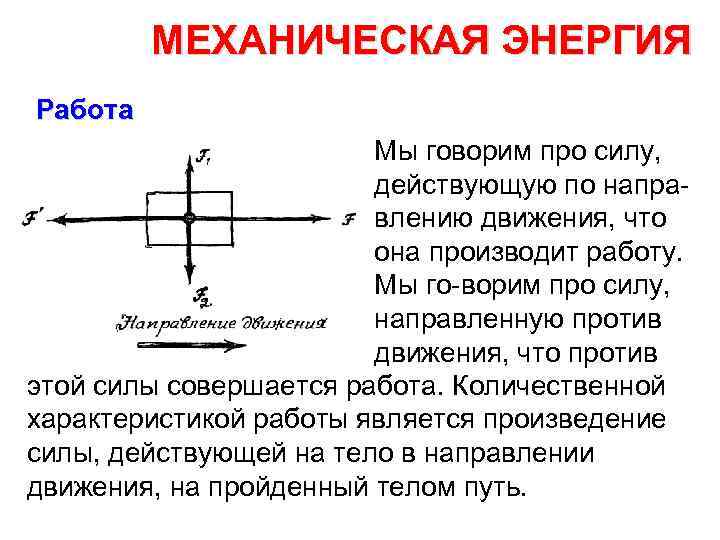
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Мы говорим про силу, действующую по напра влению движения, что она производит работу. Мы го ворим про силу, направленную против движения, что против этой силы совершается работа. Количественной характеристикой работы является произведение силы, действующей на тело в направлении движения, на пройденный телом путь.
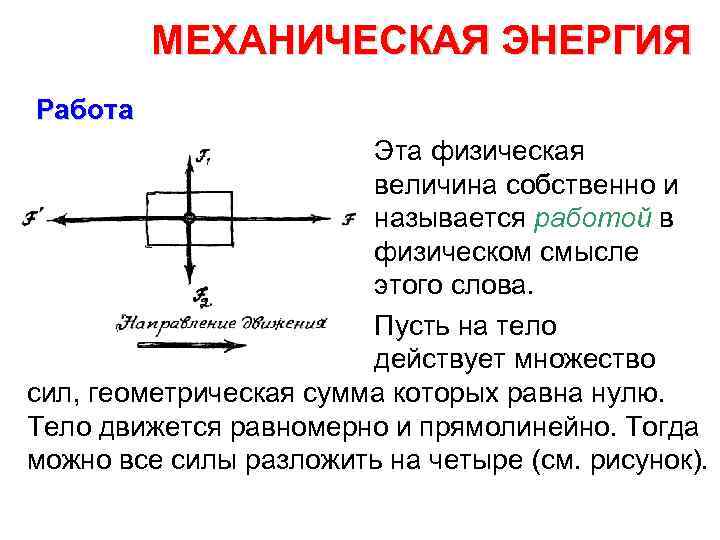
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Эта физическая величина собственно и называется работой в физическом смысле этого слова. Пусть на тело действует множество сил, геометрическая сумма которых равна нулю. Тело движется равномерно и прямолинейно. Тогда можно все силы разложить на четыре (см. рисунок).
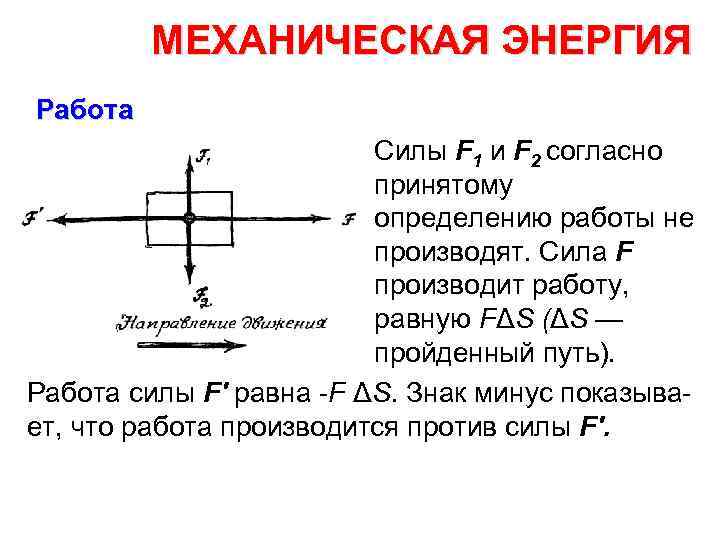
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Силы F 1 и F 2 согласно принятому определению работы не производят. Сила F производит работу, равную FΔS (ΔS — пройденный путь). Работа силы F' равна F ΔS. Знак минус показыва ет, что работа производится против силы F'.
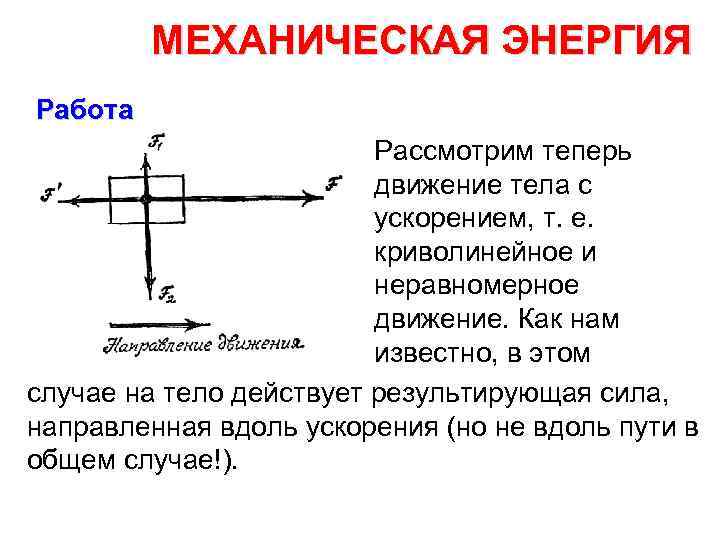
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Рассмотрим теперь движение тела с ускорением, т. е. криволинейное и неравномерное движение. Как нам известно, в этом случае на тело действует результирующая сила, направленная вдоль ускорения (но не вдоль пути в общем случае!).
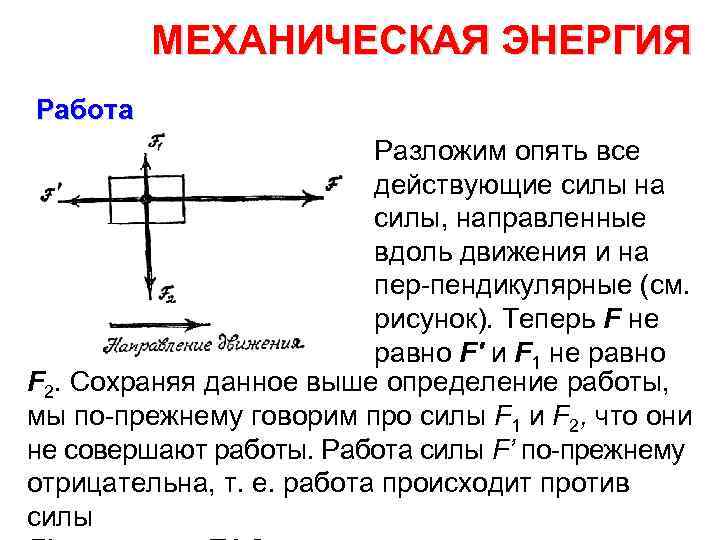
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Разложим опять все действующие силы на силы, направленные вдоль движения и на пер пендикулярные (см. рисунок). Теперь F не равно F' и F 1 не равно F 2. Сохраняя данное выше определение работы, мы по прежнему говорим про силы F 1 и F 2, что они не совершают работы. Работа силы F’ по прежнему отрицательна, т. е. работа происходит против силы
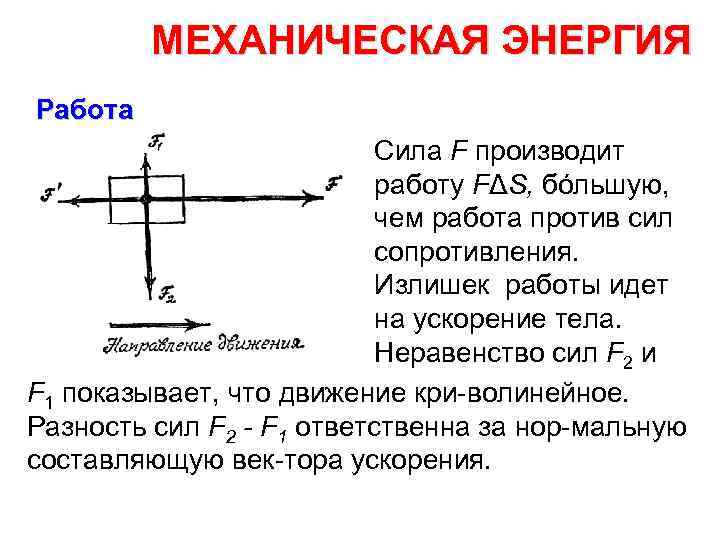
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Сила F производит работу FΔS, бóльшую, чем работа против сил сопротивления. Излишек работы идет на ускорение тела. Неравенство сил F 2 и F 1 показывает, что движение кри волинейное. Разность сил F 2 F 1 ответственна за нор мальную составляющую век тора ускорения.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Рассмотрим крайний случай — равномерное движение по окружности. Результирующая сила в таком движении направлена, как нам извест но, по радиусу окружности, т. е. перпендикулярно к направ лению движения. Поэтому центростремительная сила не производит работы. Итак, излишек работы в общем случае криволинейного уско ренного движения идет на создание не всего ускорения, а лишь тангенци альной составляющей вектора ускорения.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Работа Последнее равенство можно записать в виде FΔS=F' ΔS + mat ΔS и прочитать иначе: работа действующей силы складывается из работы против сил сопротивления и работы, затраченной на ускорение тела.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Кинетическая энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Кинетическая энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Кинетическая энергия Предыдущее уравнение читается теперь так: работа результирующей силы, дей ствующей на тело (т. е. произведение тангенциальной составляющей результирующей силы на путь), равна приращению кинетической энергии тела. Это уравнение удобно для решения элементарных механических задач, в которых задан путь, на котором действовала сила. Термин «энергия» встретится нам неоднократно. Это одно из важнейших физических понятий.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Кинетическая энергия Энергия, т. е. работоспособность, есть функция состояния тела; за счет убыли величины этой функции и произведена работа. Кинетическая энергия есть функция состояния движения. Если кинетическая энергия изменилась от K 1 до K 2, то произведенная при этом работа будет равна К 2 – К 1 вне зависимости от характера движения. Быстро или медленно, равномерно или нет менялась скорость все это не имеет значения. Убыль кинетиче ской энергии на определенную величину дает всегда одну и ту же работу.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Рассмотрим некоторые явления, при которых произведенная ра бота не сопровождается изменением скорости тела. Два типа приме ров будут занимать наше внимание: первые относятся к упругой деформации тел, вторые описывают события, происходящие при движении тел в поле тяжести и в электрическом поле. Сейчас мы по кажем, что в обоих этих случаях мы сталкиваемся с превращением работы в особую разновидность энергии, называемую потенциаль ной энергией.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Сначала остановимся на явлениях упругой деформации. Опыт по казывает, что при любой упругой деформации — растяжении, сжа тии, изгибе и т. д. — можно указать такую функцию состояния, которая возрастает как раз на величину произведенной над телом работы. Эта функция состояния или, иначе говоря, функция свойств тела и степени деформации, носит название потенциальной энергии упругости.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Покажем наличие такой энергии лишь для одного примера упру гой деформации — линейного растяжения или сжатия. Аналогич ные доказательства возможны для любых иных видов упругой де формации. Пусть некоторая сила (скажем, мускульная) очень медленно растягивает твердое тело (пружину). Работа, затраченная на растяже ние тела от длины l + s 1 до длины l + s 2, где l — длина недеформированной пружины, равна A=F(s 2 s 1).

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Совершенно такой же вид имеют формулы потенциальной энер гии упругости для других видов деформации, k характеризует жест кость тела по отношению к конкретному виду деформации, a s является мерой деформации (например, угол закручивания, угол сдвига и т. п. ). Величина Uупр является энергией именно в том смысле, о кото ром мы говорили в ассуждениях о р кинетической энергии.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Каким бы способом и с какой бы бы стротой ни было произведено деформирование тела, одной и той же затраченной работе будет соответствовать всегда одно и то же зна чение приращения величины ks 2/2. Это и значит, что ks 2/2 является мерой энергии, а именно потенциальной энергии упругости.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Силы тяжести обладают той же особенностью, что и силы упру гости, а именно: работа, затраченная на подъем тела в поле тяжести, идет на изменение функции состояния тела. В этом случае интере сующая нас функция зависит от расположения данного тела по отношению к притягивающим его телам. Она носит название по тенциальной энергии тяготения. Покажем наличие такой энергии, прежде всего, для тела, на ходящегося вблизи земной поверхности.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Допустим, тело перемести лось з одной точки в и другую, более высокую точку по какому то произвольному пути. Разобьем эту траекторию на малые кусочки и заменим кривую линию ломаной. Это можно сделать сколь угодно точно. Работа, затраченная на перемещение тела вдоль одного из таких прямоли нейных отрезков длиной l, d равна d. A = mgdl sina, или d. A = mgdh, где dh прирост высоты.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия т. е. работа перемещения равняется приросту произведения mgh, которое является мерой потенциальной энергии тяготения для этого простого случая. Вполне ясно, что U = mgh является энергией и отвечает полностью смыслу, вкладываемому нами в это слово.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия На каком бы пути ни производилась работа, по какому пути и с какой скоростью ни двигалось бы тело, работа перемещения тела из точки 1 в точку 2 будет всегда одинаковой, так как прирост энергии зависит лишь от место нахождения этих точек, в нашем простейшем случае — от их высот. Так как работа перемещения тела в поле тяготения не зависит от формы пути, то работа перемещения по замкнутому контуру будет равна нулю.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Энергия взаимодействия разноименных зарядов будет отрица тельной и будет вести себя, как гравитационная. Энергия одноимен ных зарядов равна нулю на бесконечности и растет по мере сбли жения зарядов. Этими примерами потенциальной энергии мы можем ограничить ся, хотя в разных случаях в рассмотрение могут быть введены и иные функции состояния тела.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия проявляется всегда, когда между телами или частицами, входящими в рассматриваемую систему, действуют силы, зависящие от расстояний между телами. Потенциальная энер гия есть энергия взаимодействия тел. Если система состоит из мно жества тел или частиц, то можно говорить о ее суммарной потен циальной энергии, которая складывается из энергий взаимодействия между всеми частицами (каждой с каждой).

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия Уже в случае четырех частиц потенциальная энергия будет состоять из шести слагаемых, так как надо учесть взаимодействие первого тела со вторым, третьим и четвертым, второго с третьим и четвертым и, наконец, третьего с четвертым. В механике учитывают только потенциальную энергию сил, дей ствующую между разными телами. Если тела — сложные и состоят из множества частиц, то потенциальная энергия взаимодействия этих частиц считается неизменной во время механических явлений.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальная энергия взаимодействия частиц, из которых состоит тело, входит составной частью во внутреннюю энергию тела. Если же имеют место изменения внутренней энергии тела, то яв ление должно быть рассмотрено с точки зрения законов термодина мики.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии •

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии Изменение механической энергии равно работе непотенциальных сил, а если этой работой пренебречь, то полная механическая энергия замкнутой системы тел остается не изменной сохраняется. Закон сохранения механической энергии является, с одной сто роны, следствием уравнений механики (закона Ньютона); с другой стороны, его можно рассматривать как частный случай наиболее общего закона природы — закона сохранения энергии.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии Уже в механике мы сталкиваемся с большим разнообразием различных взаимопревращений энергии. Рассматривая движение тела под действием упругих сил или сил тяготения, нетрудно заме тить, что увеличение энергии одной из механических форм сопро вождается уменьшением энергии другой формы. Так, например, силы тяжести, действующие на падающее тело, уменьшают потенциальную энергию и увеличивают кинетическую энергию тела.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии Обратный переход происходит при подъеме тела на высоту. Силы упругости, заставляющие отскочить от стенки бро шенный мяч, уменьшают потенциальную энергию сжатого мяча, ко торая переходит в кинетическую. Обратный переход происходит в момент остановки стенкой брошенного мяча (период от отсутствия деформации до максимального сжатия). Растянутая пружина может поднять груз на высоту. Напротив, падающий груз растянет пружину.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Закон сохранения механической энергии Следовательно, энергия упру гости может перейти в энергию тяготения, и наоборот. Приведенные примеры относятся как к случаям перехода одной формы энергии в другую для одного и того же тела, так и к случаям передачи энергии одним телом другому. Разумеется, возможны передачи одним телом другому энергии в той же форме: один груз тянет другой при помощи перекинутой через блок нити, один шар, столкнувшись с другим, передает ему часть своей кинетической энергии и т. д.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Потенциальная энергия взаимодействия тел или частиц зависит от их взаимного расположения, т. е. всегда является функцией коор динат или иных параметров, характеризующих положение этих тел в пространстве. В простейших случаях потенциальная энергия мо жет зависеть от дной о единственной координаты. Рассмотрим взаимодействие двух частиц, потенциальная энер гия взаимодействия которых определяется функцией U(х), где х расстояние между частицами.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие •
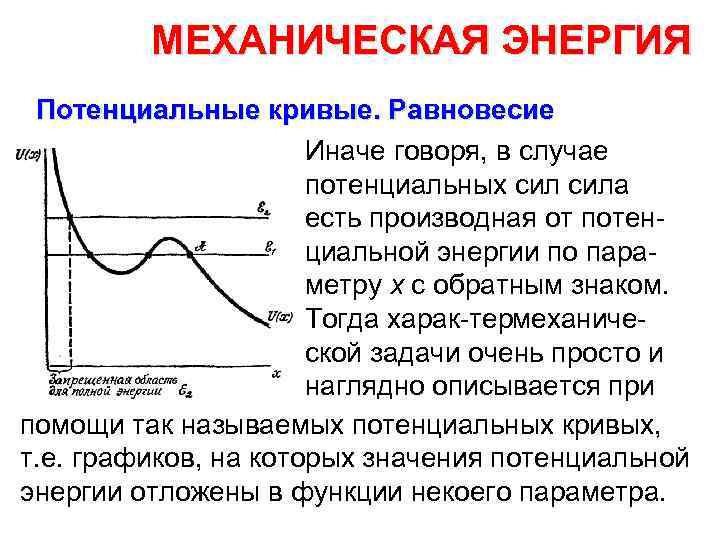
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Иначе говоря, в случае потенциальных сила есть производная от потен циальной энергии по пара метру х с обратным знаком. Тогда харак тер еханиче м ской задачи очень просто и наглядно описывается при помощи так называемых потенциальных кривых, т. е. графиков, на которых значения потенциальной энергии отложены в функции некоего параметра.
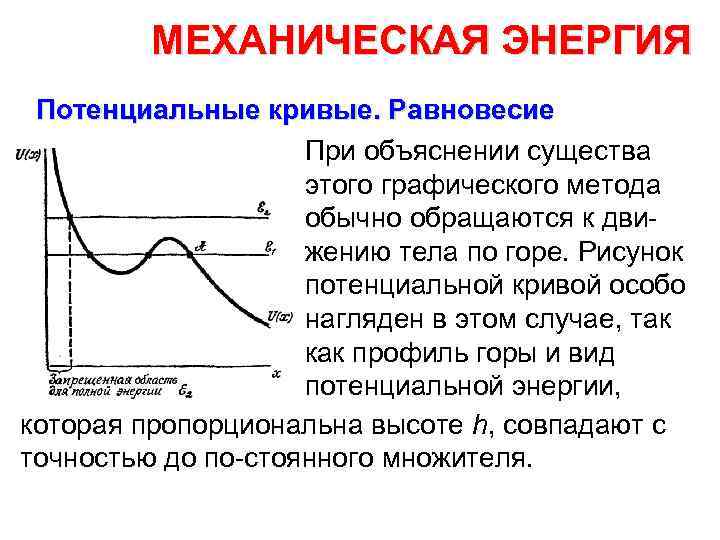
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие При объяснении существа этого графического метода обычно обращаются к дви жению тела по горе. Рисунок потенциальной кривой особо нагляден в этом случае, так как профиль горы и вид потенциальной энергии, которая пропорциональна высоте h, совпадают с точностью до по стоянного множителя.
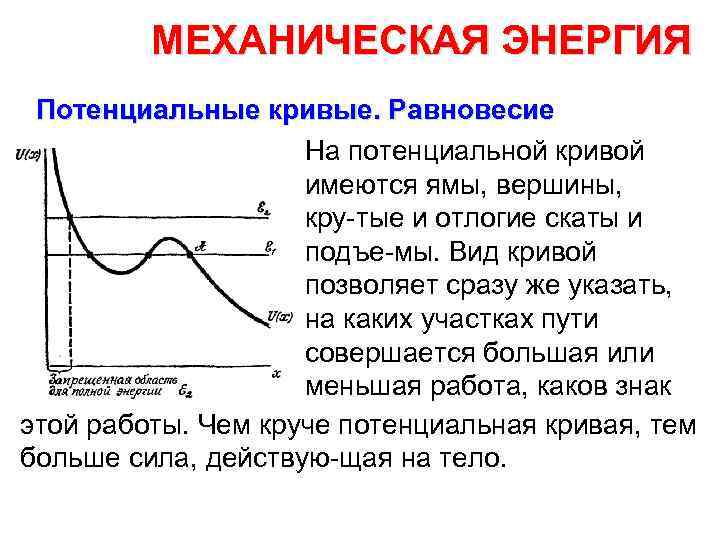
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие На потенциальной кривой имеются ямы, вершины, кру тые и отлогие скаты и подъе мы. Вид кривой позволяет сразу же указать, на каких участках пути совершается большая или меньшая работа, каков знак этой работы. Чем круче потенциальная кривая, тем больше сила, действую щая на тело.
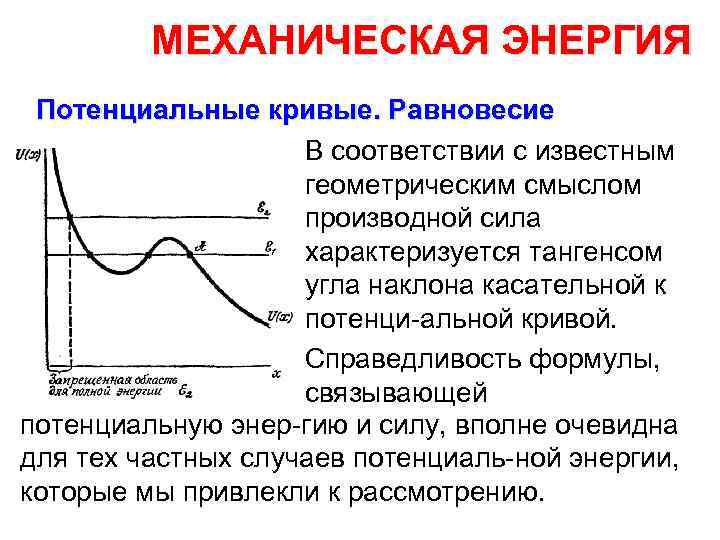
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие В соответствии с известным геометрическим смыслом производной сила характеризуется тангенсом угла наклона касательной к потенци альной кривой. Справедливость формулы, связывающей потенциальную энер гию и силу, вполне очевидна для тех частных случаев потенциаль ной энергии, которые мы привлекли к рассмотрению.
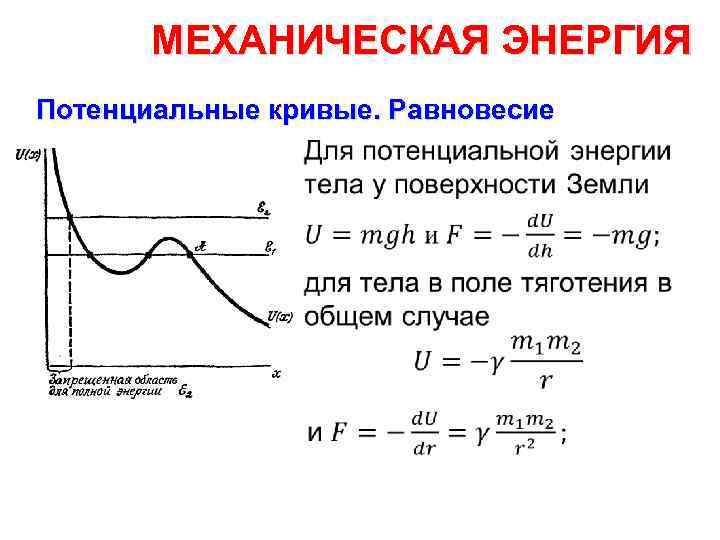
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие •
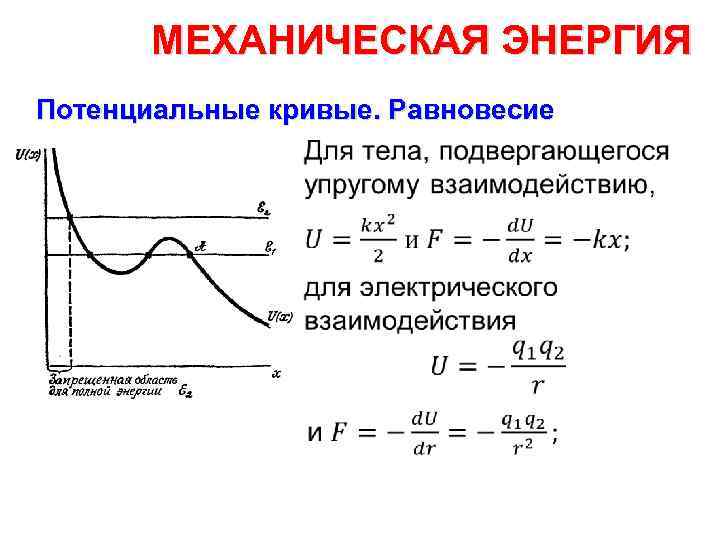
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие •
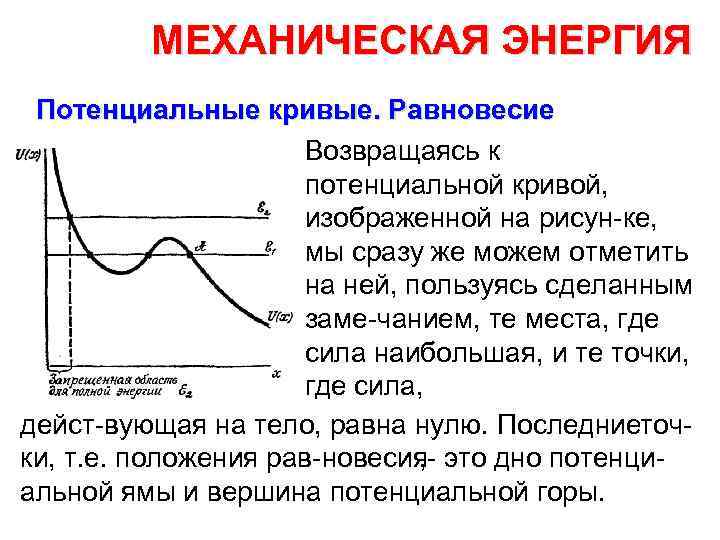
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Возвращаясь к потенциальной кривой, изображенной на рисун ке, мы сразу же можем отметить на ней, пользуясь сделанным заме чанием, те места, где сила наибольшая, и те точки, где сила, дейст вующая на тело, равна нулю. Последние оч т ки, т. е. положения рав новесия , это дно потенци альной ямы и вершина потенциальной горы.
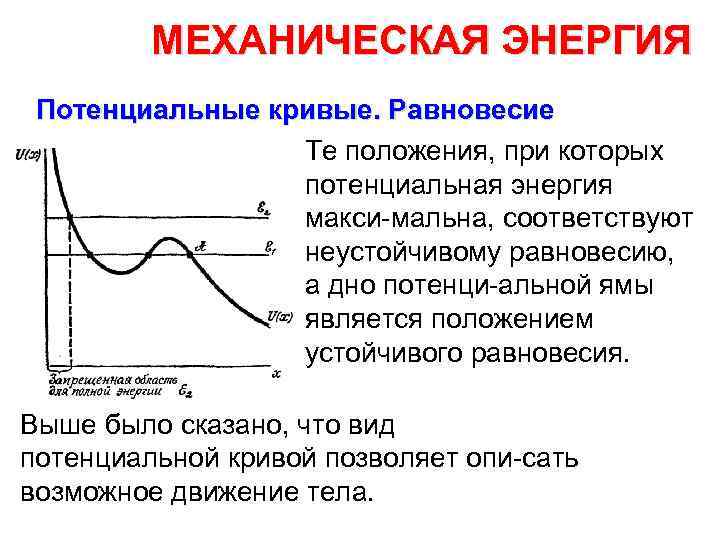
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Те положения, при которых потенциальная энергия макси мальна, соответствуют неустойчивому равновесию, а дно потенци альной ямы является положением устойчивого равновесия. Выше было сказано, что вид потенциальной кривой позволяет опи сать возможное движение тела.
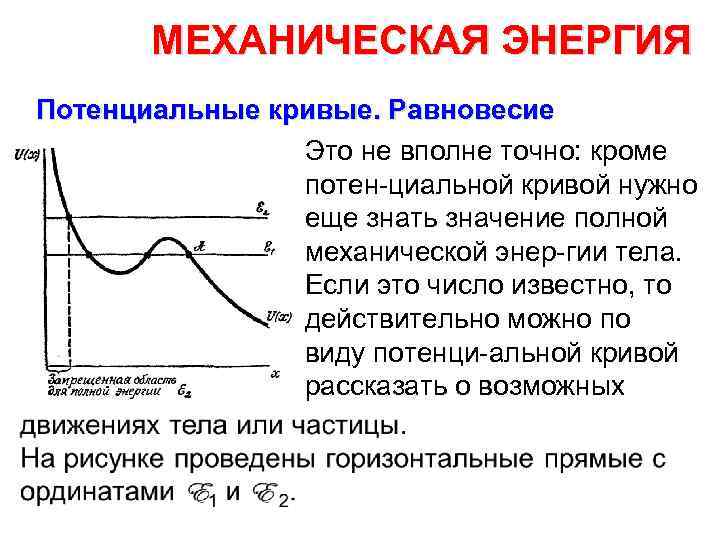
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Это не вполне точно: кроме потен циальной кривой нужно еще знать значение полной механической энер гии тела. Если это число известно, то действительно можно по виду потенци альной кривой рассказать о возможных
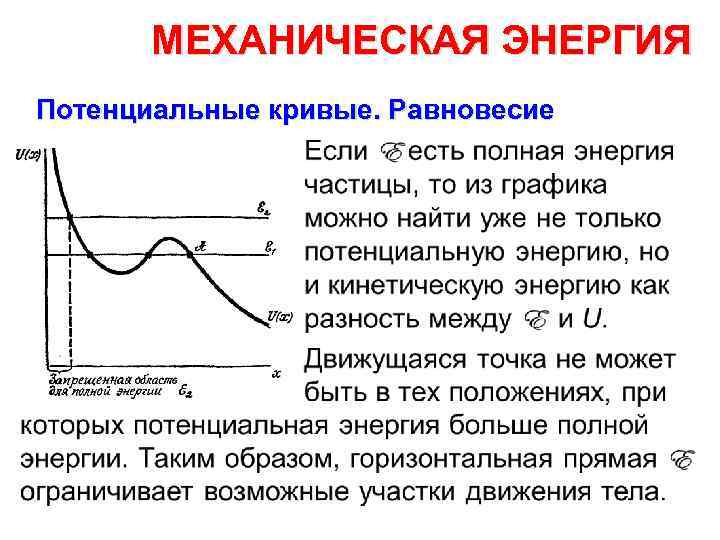
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие •
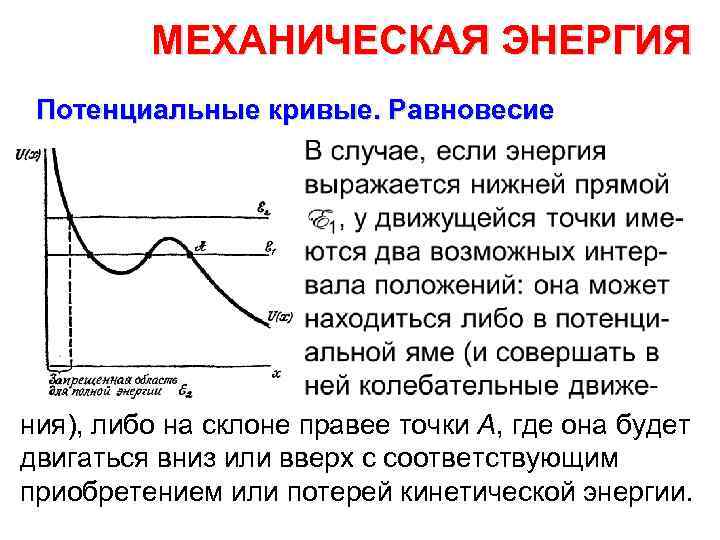
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие • ния), либо на склоне правее точки А, где она будет двигаться вниз или вверх с соответствующим приобретением или потерей кинетической энергии.
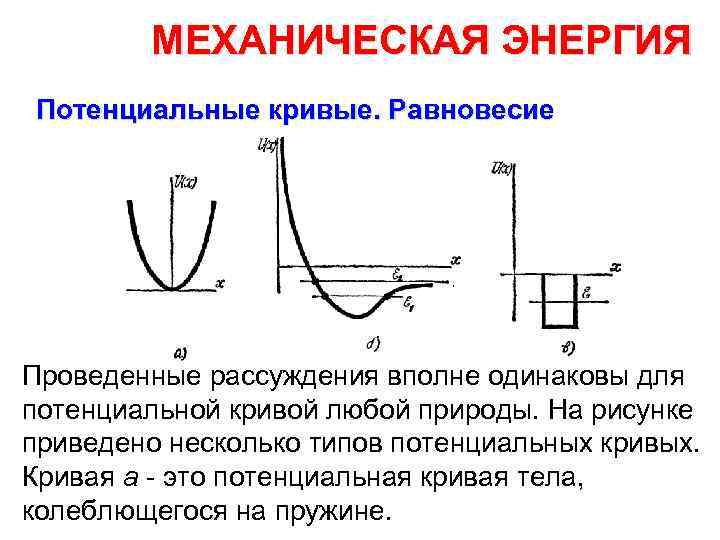
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Проведенные рассуждения вполне одинаковы для потенциальной кривой любой природы. На рисунке приведено несколько типов потенциальных кривых. Кривая а это потенциальная кривая тела, колеблющегося на пружине.
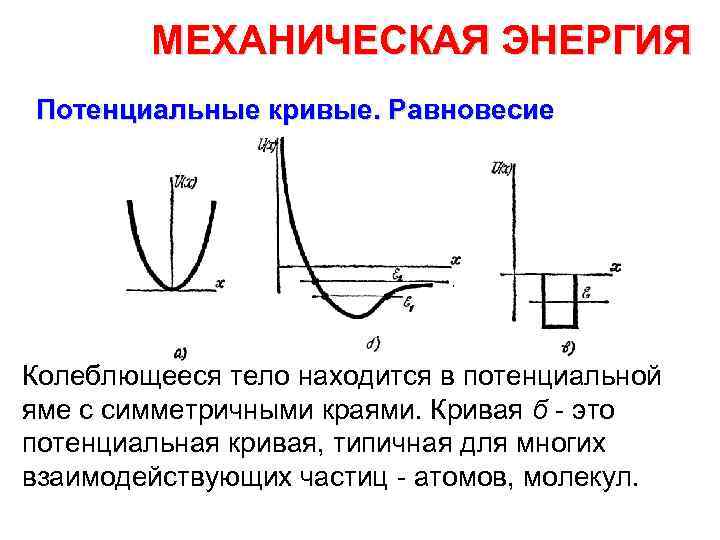
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Колеблющееся тело находится в потенциальной яме с симметричными краями. Кривая б это потенциальная кривая, типичная для многих взаимодействующих частиц атомов, молекул.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Кривая представляет собой потенци альную яму, один край которой очень крутой, а другой — пологий. По оси абсцисс отложено расстояние между частицами. Как видно из кривой, потенциальная энергия весьма велика на малых рассто яниях, увеличением расстояния она с падает, достигает минимума, затем медленно возрастает, стремясь к некоторому конечному пределу.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Характер движения и связи двух взаимодействующих частиц вполне детально описывается этой кри вой. Следует различать два случая: первый, когда полная механиче ская энергия этой пары частиц
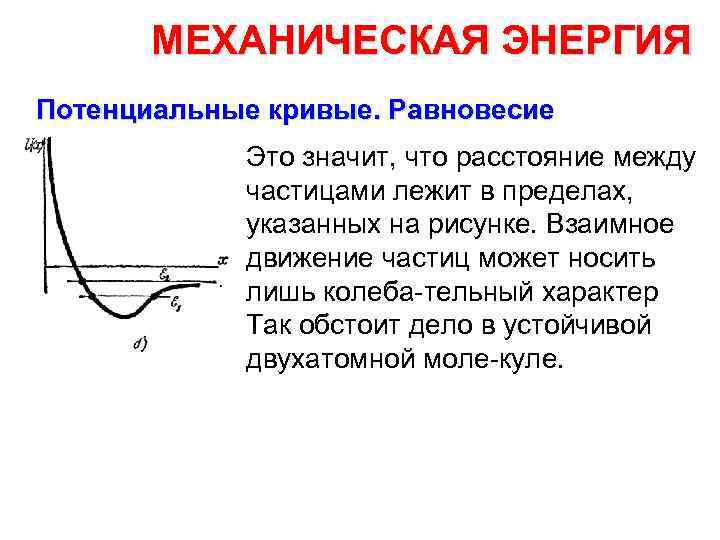
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Это значит, что расстояние между частицами лежит в пределах, указанных на рисунке. Взаимное движение частиц может носить лишь колеба тельный характер. Так обстоит дело в устойчивой двухатомной моле куле.
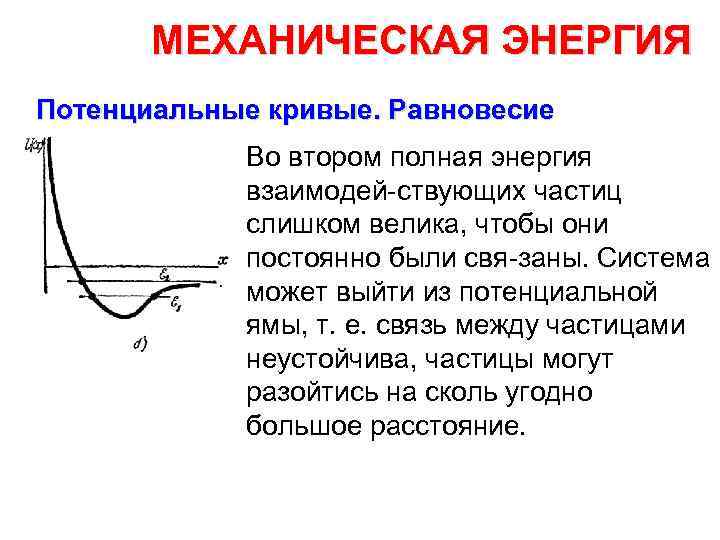
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Во втором полная энергия взаимодей ствующих частиц слишком велика, чтобы они постоянно были свя заны. Система может выйти из потенциальной ямы, т. е. связь между частицами неустойчива, частицы могут разойтись на сколь угодно большое расстояние.

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Потенциальные кривые. Равновесие Третья потенциальная кривая это так называемый потенциальный ящик. Поскольку сила характеризует ся тангенсом угла наклона касатель ной к потенциальной кривой, мы видим, что потенциальная энергия может быть представлена в виде ящика, если тело или частицы перемещаются свободно без действия сил, но не могут выйти за пределы заданного участка, пока полная энергия меньше высоты бортов ямы.
3 Механическая энергия.pptx