Метрика Хаусдорфа Выполнила: Магистрантка 2 года обучения, факультета МИФи. Т , Никифорова А. Г.
Феликс Хаусдорф Felix Hausdorff 8 ноября 1868, Бреслау — 26 января 1942, Бонн Ø Немецкий математик, один из основоположников современной топологии. Ø Окончил Лейпцигский университет (1891). Ø Стал профессором этого университета, Ø позже был профессором университетов в Грейфсвальде и Бонне.
Феликс Хаусдорф Felix Hausdorff 8 ноября 1868, Бреслау — 26 января 1942, Бонн Ø В 1935 году был отстранен от преподавательской деятельности как еврей, что было оформлено как отставка в звании почетного профессора. Ø В 1942 году, перед отправкой его и его семьи в нацистский концлагерь, покончил с собой вместе с женой и её сестрой, приняв смертельную дозу барбитала.
Научная деятельность ü ü Ø Ø Ввел и впервые исследовал важные топологические понятия: хаусдорфова пространства (1914), топологического предела, частично упорядоченного множества, хаусдорфовой размерности (1919). Внёс также большой вклад в: теорию множеств, функциональный анализ, теорию топологических групп, теорию чисел. Выступал также как писатель под псевдонимом: Поль Монгре (Paul Mongré ).
Научная деятельность С именем Хаусдорфа связаны многие математические понятия. q Теорема Хаусдорфа (Парадокс Хаусдорфа) q Хаусдорфово пространство q Метрика Хаусдорфа q Размерность Хаусдорфа
Метрика Хаусдорфа определяется на множестве K всех непустых компактных подмножеств полного метрического пространства (X, d) (как правило, в качестве X выступает евклидово пространство Rn). Таким образом, «точки» из K суть компактные множества из X.
Метрика Хаусдорфа Пусть E и F – два непустых компактных подмножества Rn Определение 1: Для произвольного множества E из пространства Rn и радиуса r>0 дилатацией (или расширением) E r>0 радиуса r (обозначается E+r), называется векторная E+r сумма E+Br(0), где Br(0) – замкнутый шар радиуса r с E+Br(0) центром в начале координат.
Метрика Хаусдорфа Пусть E и F – два непустых компактных подмножества Rn Определение 2: Расстояние Хаусдорфа между E и F
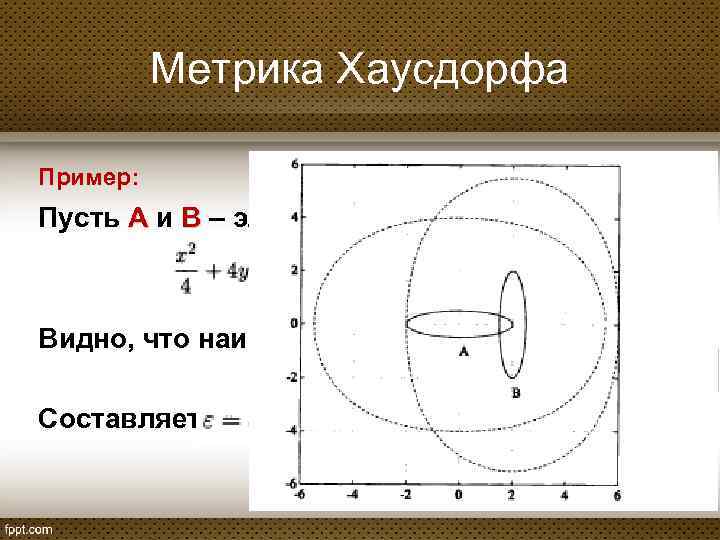
Метрика Хаусдорфа Пример: Пусть А и В – эллипсы: Видно, что наименьшее ε, при котором Составляет . Поэтому
Метрика Хаусдорфа
Метрика Хаусдорфа Пусть К – совокупность всех непустых компактных подмножеств Rn Определим расстояние между точкой х€ Rn и множеством E из Rn следующим образом: E
Метрика Хаусдорфа Пусть К – совокупность всех непустых компактных подмножеств Rn Определим расстояние между двумя компактными множествами E и F следующим образом:
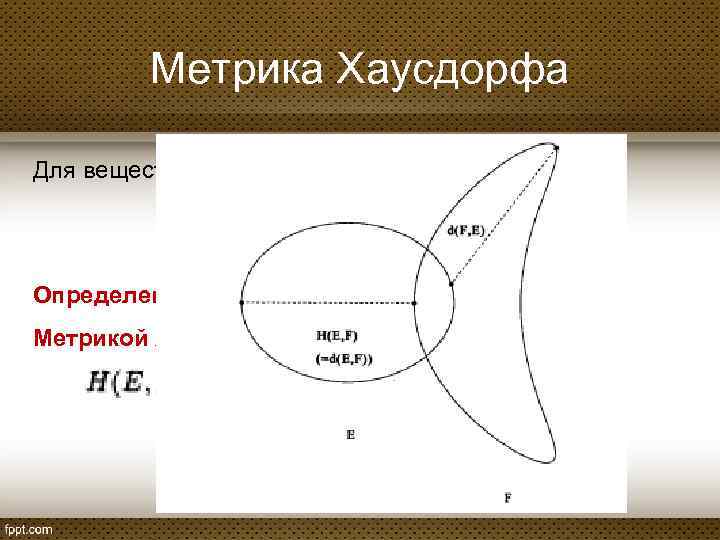
Метрика Хаусдорфа Для вещественных чисел a и b введем: Определение 2: Метрикой Хаусдорфа на К называют
Метрика Хаусдорфа
Метрика Хаусдорфа
Метрика Хаусдорфа
Метрика Хаусдорфа
Спасибо за внимание!
Скачать презентацию Метрика Хаусдорфа Выполнила Магистрантка 2 года обучения факультета
Хаусдорфова метрика (Никифорова).ppt