Метрические модели информационных процессов





05_Инфопроцессы. Метрические модели.ppt
- Количество слайдов: 9
 Метрические модели информационных процессов
Метрические модели информационных процессов
 СОДЕРЖАНИЕ 5. Метрические модели информационных процессов 5. 1. Вероятностные и вероятностно-временные характеристики информационных процессов 5. 2. Временная диаграмма выполнения информационного процесса 5. 3. ВВХ этапов доступа 5. 4. Модель процесса сохранения 5. 5. Модель процесса распространения 5. 6. Модель процесса обработки 5_Инфопроцессы. Метрические модели.
СОДЕРЖАНИЕ 5. Метрические модели информационных процессов 5. 1. Вероятностные и вероятностно-временные характеристики информационных процессов 5. 2. Временная диаграмма выполнения информационного процесса 5. 3. ВВХ этапов доступа 5. 4. Модель процесса сохранения 5. 5. Модель процесса распространения 5. 6. Модель процесса обработки 5_Инфопроцессы. Метрические модели.
 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ БАЗОВЫХ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ Характеристика – это совокупность отличительных свойств кого-либо или чего-либо. Информационные процессы носят стохастический характер, поэтому их характеризуют вероятностные и вероятностно-временные характеристики. Вероятностные характеристики задают вероятности тех или иных исходов информа- ционного процесса и его отдельных этапов. Исходы зависят от поведения коммуникан- тов, функционирования среды взаимодействия и сигнальных устройств, управляющих воздействий, помех и от других факторов, влияющих на логику процесса. Существуют желаемые и нежелательные исходы информационных процессов. Предположим, что в общем случае информационный процесс имеет K исходов, и k-й исход (k = 1, 2, …, K) достигается с вероятностью Pk. Тогда для повышения качества выполнения информаци- онного процесса при обслуживании коммуникантов надо стремиться организовать вы- полнение информационного процесса таким образом, чтобы увеличились вероятности достижения таких исходов, которые являются желаемыми. Вероятностно-временные характеристики задают время, которое требуется для дос- тижения тех или иных состояний информационного процесса. Отдельно следует рас- сматривать этапы доступа пользователей к среде взаимодействия и этапы преобразова- ния данных. Время реализации этапов является случайной величиной. 5_Инфопроцессы. Метрические модели.
ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ БАЗОВЫХ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ Характеристика – это совокупность отличительных свойств кого-либо или чего-либо. Информационные процессы носят стохастический характер, поэтому их характеризуют вероятностные и вероятностно-временные характеристики. Вероятностные характеристики задают вероятности тех или иных исходов информа- ционного процесса и его отдельных этапов. Исходы зависят от поведения коммуникан- тов, функционирования среды взаимодействия и сигнальных устройств, управляющих воздействий, помех и от других факторов, влияющих на логику процесса. Существуют желаемые и нежелательные исходы информационных процессов. Предположим, что в общем случае информационный процесс имеет K исходов, и k-й исход (k = 1, 2, …, K) достигается с вероятностью Pk. Тогда для повышения качества выполнения информаци- онного процесса при обслуживании коммуникантов надо стремиться организовать вы- полнение информационного процесса таким образом, чтобы увеличились вероятности достижения таких исходов, которые являются желаемыми. Вероятностно-временные характеристики задают время, которое требуется для дос- тижения тех или иных состояний информационного процесса. Отдельно следует рас- сматривать этапы доступа пользователей к среде взаимодействия и этапы преобразова- ния данных. Время реализации этапов является случайной величиной. 5_Инфопроцессы. Метрические модели.
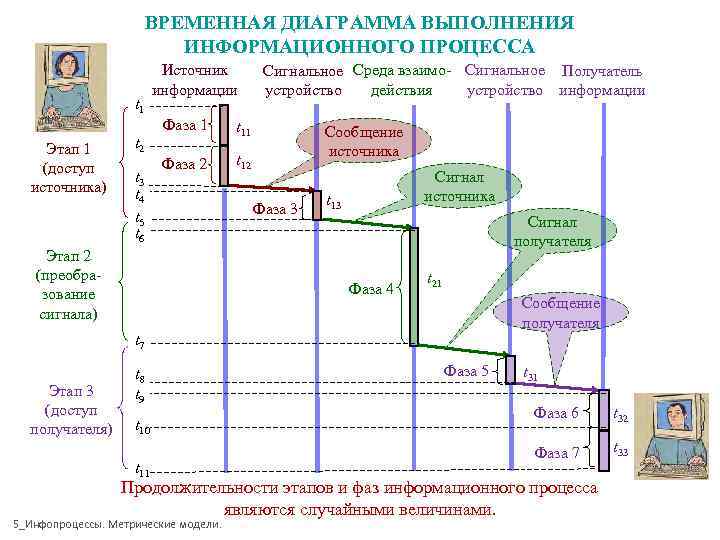
 ВРЕМЕННАЯ ДИАГРАММА ВЫПОЛНЕНИЯ ИНФОРМАЦИОННОГО ПРОЦЕССА Источник Сигнальное Среда взаимо- Сигнальное Получатель информации устройство действия устройство информации t 1 Фаза 1 t 11 Сообщение Этап 1 t 2 источника (доступ Фаза 2 t 12 t 3 Сигнал источника) t 4 t 13 источника t 5 Фаза 3 Сигнал t 6 получателя Этап 2 (преобра- t 21 зование Фаза 4 Сообщение сигнала) получателя t 7 t 8 Фаза 5 t 31 Этап 3 t 9 (доступ Фаза 6 t 32 получателя) t 10 Фаза 7 t 33 t 11 Продолжительности этапов и фаз информационного процесса являются случайными величинами. 5_Инфопроцессы. Метрические модели.
ВРЕМЕННАЯ ДИАГРАММА ВЫПОЛНЕНИЯ ИНФОРМАЦИОННОГО ПРОЦЕССА Источник Сигнальное Среда взаимо- Сигнальное Получатель информации устройство действия устройство информации t 1 Фаза 1 t 11 Сообщение Этап 1 t 2 источника (доступ Фаза 2 t 12 t 3 Сигнал источника) t 4 t 13 источника t 5 Фаза 3 Сигнал t 6 получателя Этап 2 (преобра- t 21 зование Фаза 4 Сообщение сигнала) получателя t 7 t 8 Фаза 5 t 31 Этап 3 t 9 (доступ Фаза 6 t 32 получателя) t 10 Фаза 7 t 33 t 11 Продолжительности этапов и фаз информационного процесса являются случайными величинами. 5_Инфопроцессы. Метрические модели.
 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ. ЭТАПОВ ДОСТУПА К СРЕДЕ ВЗАИМОДЕЙСТВИЯ N – количество разных этапов доступа при реализации информационных процессов, ni – количество последовательных фаз i-го этапа доступа (i = 1, 2, …, N), ti, j – время исполнения j-й фазы i-го этапа доступа (j = 1, 2, …, ni) Время реализации i-го этапа доступа информационного процесса является интег- ральной характеристикой: В общем случае время является случайной величиной и поэтому полностью харак- теризуется функцией распределения вероятностей . Тогда случайное время реализации этапа доступа информационного процесса можно определить при помощи операции свертки случайных величин: Коммуникант заинтересован в том, чтобы время выполнения этапов информационного процесса укладывалось в определенные рамки. Эти требования к продолжительности этапа можно задать интервалом времени Если полученное время выполнения этапа удовлетворяет соотношению то этап выполнен за допустимое время. 5_Инфопроцессы. Метрические модели.
ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ. ЭТАПОВ ДОСТУПА К СРЕДЕ ВЗАИМОДЕЙСТВИЯ N – количество разных этапов доступа при реализации информационных процессов, ni – количество последовательных фаз i-го этапа доступа (i = 1, 2, …, N), ti, j – время исполнения j-й фазы i-го этапа доступа (j = 1, 2, …, ni) Время реализации i-го этапа доступа информационного процесса является интег- ральной характеристикой: В общем случае время является случайной величиной и поэтому полностью харак- теризуется функцией распределения вероятностей . Тогда случайное время реализации этапа доступа информационного процесса можно определить при помощи операции свертки случайных величин: Коммуникант заинтересован в том, чтобы время выполнения этапов информационного процесса укладывалось в определенные рамки. Эти требования к продолжительности этапа можно задать интервалом времени Если полученное время выполнения этапа удовлетворяет соотношению то этап выполнен за допустимое время. 5_Инфопроцессы. Метрические модели.
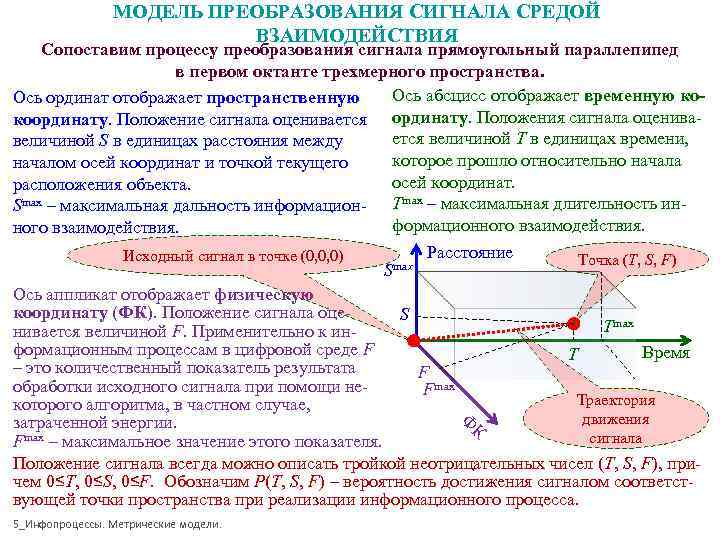
 МОДЕЛЬ ПРЕОБРАЗОВАНИЯ СИГНАЛА СРЕДОЙ ВЗАИМОДЕЙСТВИЯ Сопоставим процессу преобразования сигнала прямоугольный параллепипед в первом октанте трехмерного пространства. Ось ординат отображает пространственную Ось абсцисс отображает временную ко- координату. Положение сигнала оценивается ординату. Положения сигнала оценива- величиной S в единицах расстояния между ется величиной T в единицах времени, началом осей координат и точкой текущего которое прошло относительно начала расположения объекта. осей координат. Smax – максимальная дальность информацион- Tmax – максимальная длительность ин- ного взаимодействия. формационного взаимодействия. Исходный сигнал в точке (0, 0, 0) Расстояние Точка (T, S, F) Smax Ось аппликат отображает физическую координату (ФК). Положение сигнала оце- S нивается величиной F. Применительно к ин- Tmax формационным процессам в цифровой среде F T Время – это количественный показатель результата F обработки исходного сигнала при помощи не- Fmax которого алгоритма, в частном случае, Траектория затраченной энергии. Ф движения К Fmax – максимальное значение этого показателя. сигнала Положение сигнала всегда можно описать тройкой неотрицательных чисел (T, S, F), при- чем 0≤T, 0≤S, 0≤F. Обозначим P(T, S, F) – вероятность достижения сигналом соответст- вующей точки пространства при реализации информационного процесса. 5_Инфопроцессы. Метрические модели.
МОДЕЛЬ ПРЕОБРАЗОВАНИЯ СИГНАЛА СРЕДОЙ ВЗАИМОДЕЙСТВИЯ Сопоставим процессу преобразования сигнала прямоугольный параллепипед в первом октанте трехмерного пространства. Ось ординат отображает пространственную Ось абсцисс отображает временную ко- координату. Положение сигнала оценивается ординату. Положения сигнала оценива- величиной S в единицах расстояния между ется величиной T в единицах времени, началом осей координат и точкой текущего которое прошло относительно начала расположения объекта. осей координат. Smax – максимальная дальность информацион- Tmax – максимальная длительность ин- ного взаимодействия. формационного взаимодействия. Исходный сигнал в точке (0, 0, 0) Расстояние Точка (T, S, F) Smax Ось аппликат отображает физическую координату (ФК). Положение сигнала оце- S нивается величиной F. Применительно к ин- Tmax формационным процессам в цифровой среде F T Время – это количественный показатель результата F обработки исходного сигнала при помощи не- Fmax которого алгоритма, в частном случае, Траектория затраченной энергии. Ф движения К Fmax – максимальное значение этого показателя. сигнала Положение сигнала всегда можно описать тройкой неотрицательных чисел (T, S, F), при- чем 0≤T, 0≤S, 0≤F. Обозначим P(T, S, F) – вероятность достижения сигналом соответст- вующей точки пространства при реализации информационного процесса. 5_Инфопроцессы. Метрические модели.
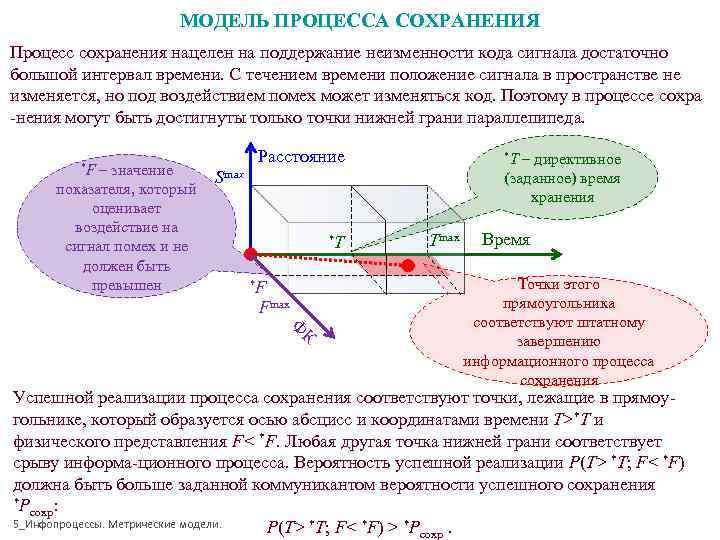
 МОДЕЛЬ ПРОЦЕССА СОХРАНЕНИЯ Процесс сохранения нацелен на поддержание неизменности кода сигнала достаточно большой интервал времени. С течением времени положение сигнала в пространстве не изменяется, но под воздействием помех может изменяться код. Поэтому в процессе сохра -нения могут быть достигнуты только точки нижней грани параллепипеда. *F Расстояние *T – директивное – значение Smax (заданное) время показателя, который хранения оценивает воздействие на сигнал помех и не *T Tmax Время должен быть превышен *F Точки этого Fmax прямоугольника Ф соответствуют штатному К завершению информационного процесса сохранения Успешной реализации процесса сохранения соответствуют точки, лежащие в прямоу- гольнике, который образуется осью абсцисс и координатами времени T>*T и физического представления F< *F. Любая другая точка нижней грани соответствует срыву информа-ционного процесса. Вероятность успешной реализации P(T> *T; F< *F) должна быть больше заданной коммуникантом вероятности успешного сохранения *P сохр: 5_Инфопроцессы. Метрические модели. P(T> *T; F< *F) > *Pсохр.
МОДЕЛЬ ПРОЦЕССА СОХРАНЕНИЯ Процесс сохранения нацелен на поддержание неизменности кода сигнала достаточно большой интервал времени. С течением времени положение сигнала в пространстве не изменяется, но под воздействием помех может изменяться код. Поэтому в процессе сохра -нения могут быть достигнуты только точки нижней грани параллепипеда. *F Расстояние *T – директивное – значение Smax (заданное) время показателя, который хранения оценивает воздействие на сигнал помех и не *T Tmax Время должен быть превышен *F Точки этого Fmax прямоугольника Ф соответствуют штатному К завершению информационного процесса сохранения Успешной реализации процесса сохранения соответствуют точки, лежащие в прямоу- гольнике, который образуется осью абсцисс и координатами времени T>*T и физического представления F< *F. Любая другая точка нижней грани соответствует срыву информа-ционного процесса. Вероятность успешной реализации P(T> *T; F< *F) должна быть больше заданной коммуникантом вероятности успешного сохранения *P сохр: 5_Инфопроцессы. Метрические модели. P(T> *T; F< *F) > *Pсохр.
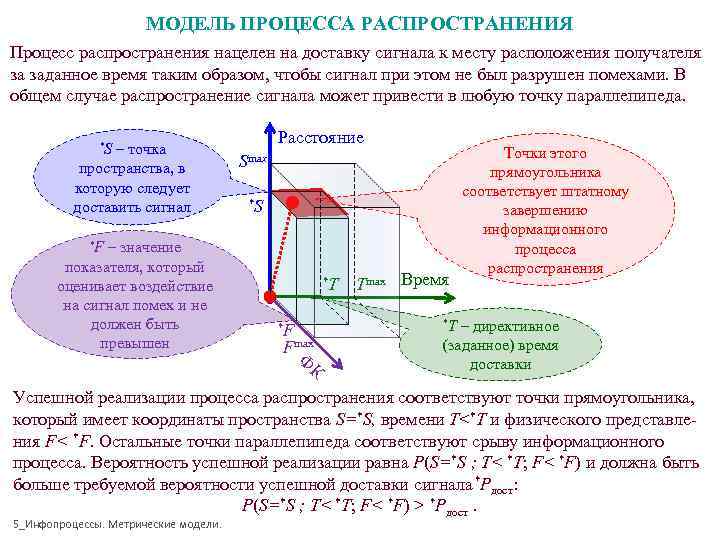
 МОДЕЛЬ ПРОЦЕССА РАСПРОСТРАНЕНИЯ Процесс распространения нацелен на доставку сигнала к месту расположения получателя за заданное время таким образом, чтобы сигнал при этом не был разрушен помехами. В общем случае распространение сигнала может привести в любую точку параллепипеда. *S Расстояние – точка Точки этого пространства, в Smax прямоугольника которую следует соответствует штатному доставить сигнал *S завершению информационного *F– значение процесса показателя, который распространения оценивает воздействие *T Tmax Время на сигнал помех и не должен быть *F *T – директивное превышен Fmax (заданное) время Ф доставки К Успешной реализации процесса распространения соответствуют точки прямоугольника, который имеет координаты пространства S=*S, времени T<*T и физического представле- ния F< *F. Остальные точки параллепипеда соответствуют срыву информационного процесса. Вероятность успешной реализации равна P(S=*S ; T< *T; F< *F) и должна быть больше требуемой вероятности успешной доставки сигнала*Pдост: P(S=*S ; T< *T; F< *F) > *Pдост. 5_Инфопроцессы. Метрические модели.
МОДЕЛЬ ПРОЦЕССА РАСПРОСТРАНЕНИЯ Процесс распространения нацелен на доставку сигнала к месту расположения получателя за заданное время таким образом, чтобы сигнал при этом не был разрушен помехами. В общем случае распространение сигнала может привести в любую точку параллепипеда. *S Расстояние – точка Точки этого пространства, в Smax прямоугольника которую следует соответствует штатному доставить сигнал *S завершению информационного *F– значение процесса показателя, который распространения оценивает воздействие *T Tmax Время на сигнал помех и не должен быть *F *T – директивное превышен Fmax (заданное) время Ф доставки К Успешной реализации процесса распространения соответствуют точки прямоугольника, который имеет координаты пространства S=*S, времени T<*T и физического представле- ния F< *F. Остальные точки параллепипеда соответствуют срыву информационного процесса. Вероятность успешной реализации равна P(S=*S ; T< *T; F< *F) и должна быть больше требуемой вероятности успешной доставки сигнала*Pдост: P(S=*S ; T< *T; F< *F) > *Pдост. 5_Инфопроцессы. Метрические модели.
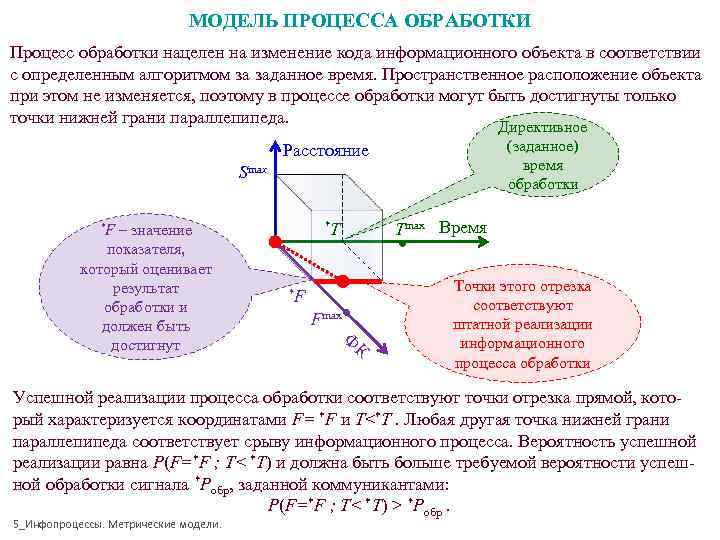
 МОДЕЛЬ ПРОЦЕССА ОБРАБОТКИ Процесс обработки нацелен на изменение кода информационного объекта в соответствии с определенным алгоритмом за заданное время. Пространственное расположение объекта при этом не изменяется, поэтому в процессе обработки могут быть достигнуты только точки нижней грани параллепипеда. Директивное Расстояние (заданное) время Smax обработки *F – значение показателя, который оценивает *T Tmax Время результат обработки и должен быть *F Fmax Ф Точки этого отрезка соответствуют штатной реализации достигнут К информационного процесса обработки Успешной реализации процесса обработки соответствуют точки отрезка прямой, кото- рый характеризуется координатами F= *F и T<*T. Любая другая точка нижней грани параллепипеда соответствует срыву информационного процесса. Вероятность успешной реализации равна P(F=*F ; T< *T) и должна быть больше требуемой вероятности успеш- ной обработки сигнала *Pобр, заданной коммуникантами: P(F=*F ; T< *T) > *Pобр. 5_Инфопроцессы. Метрические модели.
МОДЕЛЬ ПРОЦЕССА ОБРАБОТКИ Процесс обработки нацелен на изменение кода информационного объекта в соответствии с определенным алгоритмом за заданное время. Пространственное расположение объекта при этом не изменяется, поэтому в процессе обработки могут быть достигнуты только точки нижней грани параллепипеда. Директивное Расстояние (заданное) время Smax обработки *F – значение показателя, который оценивает *T Tmax Время результат обработки и должен быть *F Fmax Ф Точки этого отрезка соответствуют штатной реализации достигнут К информационного процесса обработки Успешной реализации процесса обработки соответствуют точки отрезка прямой, кото- рый характеризуется координатами F= *F и T<*T. Любая другая точка нижней грани параллепипеда соответствует срыву информационного процесса. Вероятность успешной реализации равна P(F=*F ; T< *T) и должна быть больше требуемой вероятности успеш- ной обработки сигнала *Pобр, заданной коммуникантами: P(F=*F ; T< *T) > *Pобр. 5_Инфопроцессы. Метрические модели.

