МВЭ - часть 1-2006.ppt
- Количество слайдов: 154
 Методы вычислительного эксперимента 1
Методы вычислительного эксперимента 1
 Введение 2
Введение 2
 0. Введение. Общие сведения. l Объем курса – 34 часа лекции 72 часа лабораторные занятия l Лабораторные занятия проводятся в классе ПЭВМ и выполняются в среде пакета Mathematica l Форма отчетности – экзамен (5 семестр) l Преподавание обеспечивает кафедра кибернетики l Лектор – Воротницкий Юрий Иосифович 3
0. Введение. Общие сведения. l Объем курса – 34 часа лекции 72 часа лабораторные занятия l Лабораторные занятия проводятся в классе ПЭВМ и выполняются в среде пакета Mathematica l Форма отчетности – экзамен (5 семестр) l Преподавание обеспечивает кафедра кибернетики l Лектор – Воротницкий Юрий Иосифович 3
 0. Введение. Цели и задачи дисциплины. Ознакомить с фундаментальными основами дисциплины «Методы вычислительного эксперимента» l Дать необходимые знания в области построения конструктивных вычислительных алгоритмов для решения типовых задач математического моделирования в радиофизике и электронике l Сформировать навыки формализации, разработки математических моделей и реализации вычислительных алгоритмов задач поиска оптимальных решений l 4
0. Введение. Цели и задачи дисциплины. Ознакомить с фундаментальными основами дисциплины «Методы вычислительного эксперимента» l Дать необходимые знания в области построения конструктивных вычислительных алгоритмов для решения типовых задач математического моделирования в радиофизике и электронике l Сформировать навыки формализации, разработки математических моделей и реализации вычислительных алгоритмов задач поиска оптимальных решений l 4
 0. Введение. Литература. Основная 1. Давыдов Э. Г. Исследование операций. – М. : Высшая школа, 1990. 2. Дегтярев Ю. И. Исследование операций. – М. : Высшая школа, 1986. 3. Базара М. , Шетти К. Нелинейное программирование. Теория и алгоритмы. – М. : Мир, 1982. Химмельблау Д. Прикладное нелинейное программирование. – М. : Мир, 1975 Дополнительная 1. Таха Х. Введение в исследование операций. : Пер. с англ. – М. : Издательский дом «Вильямс» , 2001. 2. Ахо А. В. , Хопкрофт Дж. Э. , Ульман Дж. Д. Структуры данных и алгоритмы. – М. : Издательский дом «Вильямс» , 2000. 3. Поляк Б. Т. Введение в оптимизацию. – М. : Наука, 1983. 5
0. Введение. Литература. Основная 1. Давыдов Э. Г. Исследование операций. – М. : Высшая школа, 1990. 2. Дегтярев Ю. И. Исследование операций. – М. : Высшая школа, 1986. 3. Базара М. , Шетти К. Нелинейное программирование. Теория и алгоритмы. – М. : Мир, 1982. Химмельблау Д. Прикладное нелинейное программирование. – М. : Мир, 1975 Дополнительная 1. Таха Х. Введение в исследование операций. : Пер. с англ. – М. : Издательский дом «Вильямс» , 2001. 2. Ахо А. В. , Хопкрофт Дж. Э. , Ульман Дж. Д. Структуры данных и алгоритмы. – М. : Издательский дом «Вильямс» , 2000. 3. Поляк Б. Т. Введение в оптимизацию. – М. : Наука, 1983. 5
 0. Введение. 0. 1. Предмет дисциплины. Вычислительный эксперимент – методология исследования сложных научных проблем, основанная на построении и анализе с помощью ЭВМ математических моделей изучаемых объектов. l Суть эксперимента: исследование объекта с целью изучения его характеристик в зависимости от условий эксперимента. l Цели эксперимента: l l l Проверка гипотез, установление новых законов и закономерностей окружающего нас мира. Целенаправленный поиск параметров объекта, обеспечивающих наилучшие (заданные) характеристики 6
0. Введение. 0. 1. Предмет дисциплины. Вычислительный эксперимент – методология исследования сложных научных проблем, основанная на построении и анализе с помощью ЭВМ математических моделей изучаемых объектов. l Суть эксперимента: исследование объекта с целью изучения его характеристик в зависимости от условий эксперимента. l Цели эксперимента: l l l Проверка гипотез, установление новых законов и закономерностей окружающего нас мира. Целенаправленный поиск параметров объекта, обеспечивающих наилучшие (заданные) характеристики 6
 0. Введение. 0. 1. Предмет дисциплины. l Что позволяет вычислительный эксперимент: l Расширение области экспериментальных исследований l l Исследование недоступных объектов Исследование несуществующих объектов Возможность изменения физических законов Расширение сферы теоретических исследований: l l Новые методы описания моделей (алгоритмическое описание) Применение методов оптимального проектирования для поиска параметров объекта исследования с наилучшими характеристиками 7
0. Введение. 0. 1. Предмет дисциплины. l Что позволяет вычислительный эксперимент: l Расширение области экспериментальных исследований l l Исследование недоступных объектов Исследование несуществующих объектов Возможность изменения физических законов Расширение сферы теоретических исследований: l l Новые методы описания моделей (алгоритмическое описание) Применение методов оптимального проектирования для поиска параметров объекта исследования с наилучшими характеристиками 7
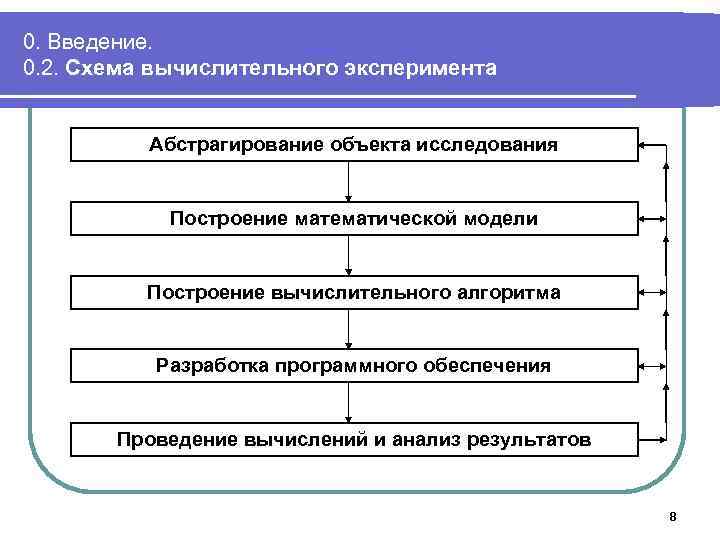 0. Введение. 0. 2. Схема вычислительного эксперимента Абстрагирование объекта исследования Построение математической модели Построение вычислительного алгоритма Разработка программного обеспечения Проведение вычислений и анализ результатов 8
0. Введение. 0. 2. Схема вычислительного эксперимента Абстрагирование объекта исследования Построение математической модели Построение вычислительного алгоритма Разработка программного обеспечения Проведение вычислений и анализ результатов 8
 0. Введение. 0. 2. Схема вычислительного эксперимента l Абстрагирование объекта исследования: l l l Определение главных (учитываемых) и второстепенных (отбрасываемых) факторов. Формулировка физических законов, на основании которых будет строиться модель. Оценка границ применимости модели. l Результат - физическая модель l Построение математической модели: l l Формализация – представление модели в математической форме Предварительное исследование математической модели (корректность, существование и единственность решения). Оценка границ применимости модели. Результат - математическая модель 9
0. Введение. 0. 2. Схема вычислительного эксперимента l Абстрагирование объекта исследования: l l l Определение главных (учитываемых) и второстепенных (отбрасываемых) факторов. Формулировка физических законов, на основании которых будет строиться модель. Оценка границ применимости модели. l Результат - физическая модель l Построение математической модели: l l Формализация – представление модели в математической форме Предварительное исследование математической модели (корректность, существование и единственность решения). Оценка границ применимости модели. Результат - математическая модель 9
 0. Введение. 0. 2. Схема вычислительного эксперимента l Построение вычислительного алгоритма: l l l Дискретизация математической модели Разработка алгоритма Предварительное исследование алгоритма (выполнимость, конечность, вычислительная сложность, устойчивость и др. ) l Результат – алгоритмическая модель l Разработка программного обеспечения: l l l Выбор технологий и средств проектирования и программирования Проектирование Кодирование (написание текста программы) Верификация, отладка, тестирование. Результат - программная модель 10
0. Введение. 0. 2. Схема вычислительного эксперимента l Построение вычислительного алгоритма: l l l Дискретизация математической модели Разработка алгоритма Предварительное исследование алгоритма (выполнимость, конечность, вычислительная сложность, устойчивость и др. ) l Результат – алгоритмическая модель l Разработка программного обеспечения: l l l Выбор технологий и средств проектирования и программирования Проектирование Кодирование (написание текста программы) Верификация, отладка, тестирование. Результат - программная модель 10
 0. Введение. 0. 2. Схема вычислительного эксперимента l Проведение вычислений и анализ результатов: l l l Планирование вычислительного эксперимента. Проведение расчётов на ЭВМ. Анализ расчётов с целью установления новых следствий из законов поведения объекта, оптимизация его параметров. Уточнение границ применимости физической и математической моделей, алгоритмов и программных средств Результат - завершение исследований, либо корректировка физической, математической, алгоритмической, программной моделей и повторение цикла вычислительного эксперимента 11
0. Введение. 0. 2. Схема вычислительного эксперимента l Проведение вычислений и анализ результатов: l l l Планирование вычислительного эксперимента. Проведение расчётов на ЭВМ. Анализ расчётов с целью установления новых следствий из законов поведения объекта, оптимизация его параметров. Уточнение границ применимости физической и математической моделей, алгоритмов и программных средств Результат - завершение исследований, либо корректировка физической, математической, алгоритмической, программной моделей и повторение цикла вычислительного эксперимента 11
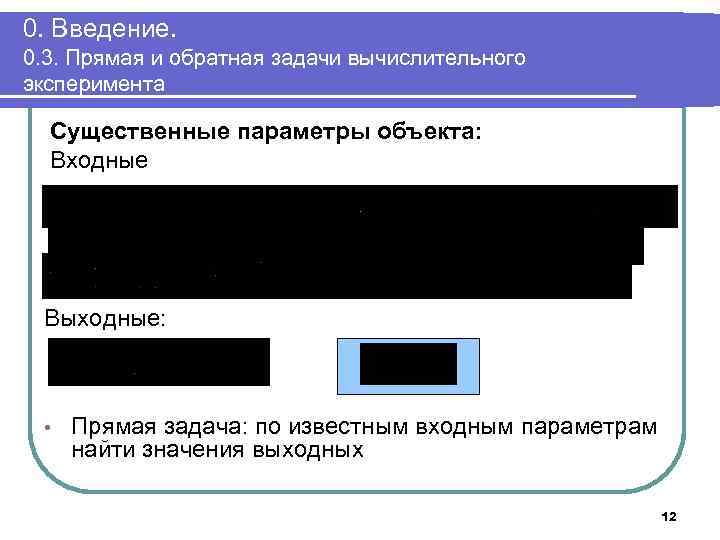 0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента Существенные параметры объекта: Входные Выходные: • Прямая задача: по известным входным параметрам найти значения выходных 12
0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента Существенные параметры объекта: Входные Выходные: • Прямая задача: по известным входным параметрам найти значения выходных 12
 0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента • Обратная задача: по известным выходным параметрам восстановить значения выходных - известны - полностью или частично неизвестны • При невозможности построения обратного оператора B -1 обычно строится итерационный процесс 13
0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента • Обратная задача: по известным выходным параметрам восстановить значения выходных - известны - полностью или частично неизвестны • При невозможности построения обратного оператора B -1 обычно строится итерационный процесс 13
 0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента • Задача оптимизации: найти значения независимых внутренних параметров, приближающих выходные характеристики к заданным - известны - заданы - требуется найти 14
0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента • Задача оптимизации: найти значения независимых внутренних параметров, приближающих выходные характеристики к заданным - известны - заданы - требуется найти 14
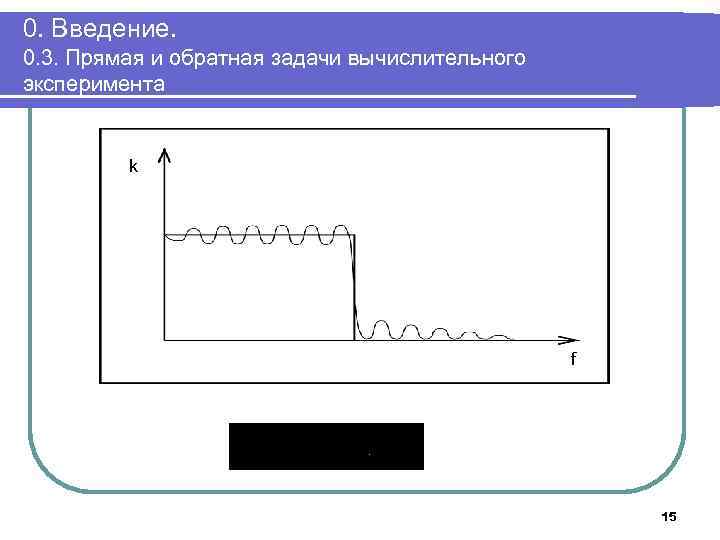 0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента k f 15
0. Введение. 0. 3. Прямая и обратная задачи вычислительного эксперимента k f 15
 Модели. Дискретизация 16
Модели. Дискретизация 16
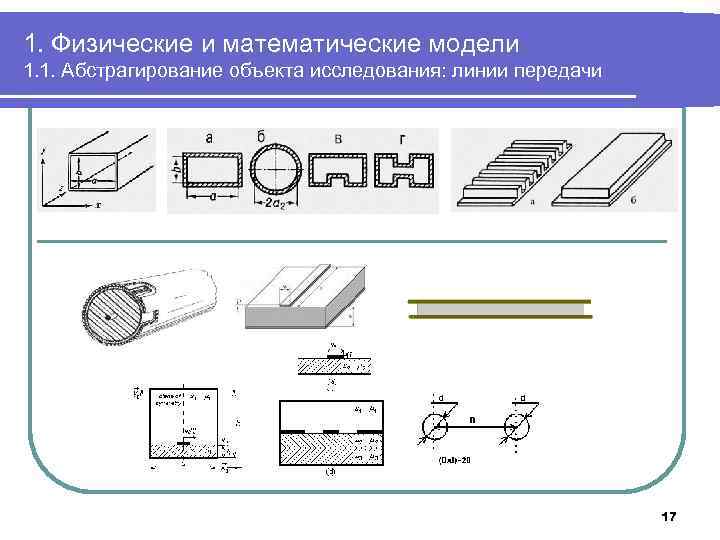 1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи 17
1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи 17
 1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи Будем рассматривать двухпроводные линии передачи l Ограничимся квазистатическим приближением (поперечная ТЕМ – волна) l l l Потерями на излучение пренебрегаем l l В качестве входных параметров модели можно использовать обобщенные параметры: погонные емкость, сопротивление, индуктивность, проводимость Модель линейная l l Описывать волновой процесс будем в терминах токов и напряжений в линии как функций координаты и времени Параметры линии не зависят от величин токов и напряжений Анализ границ применимости 18
1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи Будем рассматривать двухпроводные линии передачи l Ограничимся квазистатическим приближением (поперечная ТЕМ – волна) l l l Потерями на излучение пренебрегаем l l В качестве входных параметров модели можно использовать обобщенные параметры: погонные емкость, сопротивление, индуктивность, проводимость Модель линейная l l Описывать волновой процесс будем в терминах токов и напряжений в линии как функций координаты и времени Параметры линии не зависят от величин токов и напряжений Анализ границ применимости 18
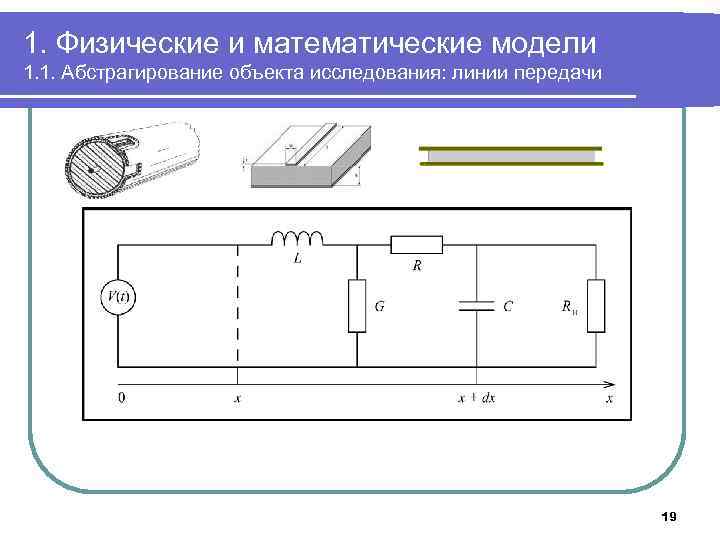 1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи 19
1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи 19
 1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи Существенные параметры объекта: Входные: Выходные: Независимые Внешние воздействия: Физические законы: Закон сохранения электрического заряда Закон Ома для участка цепи 20
1. Физические и математические модели 1. 1. Абстрагирование объекта исследования: линии передачи Существенные параметры объекта: Входные: Выходные: Независимые Внешние воздействия: Физические законы: Закон сохранения электрического заряда Закон Ома для участка цепи 20
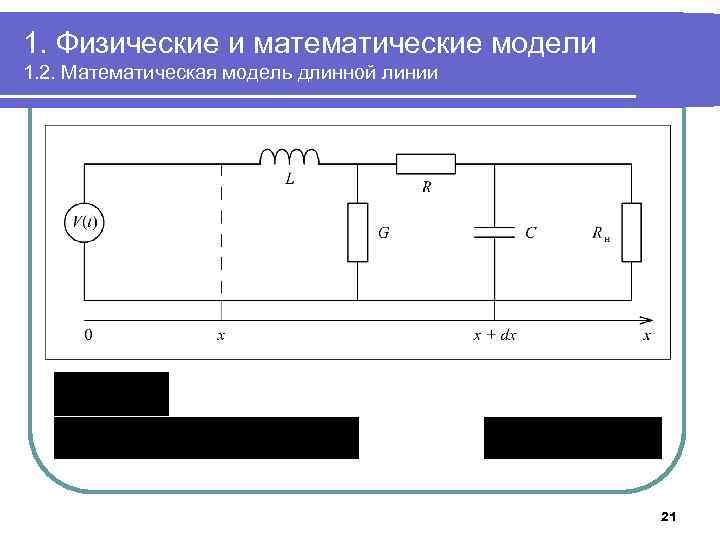 1. Физические и математические модели 1. 2. Математическая модель длинной линии 21
1. Физические и математические модели 1. 2. Математическая модель длинной линии 21
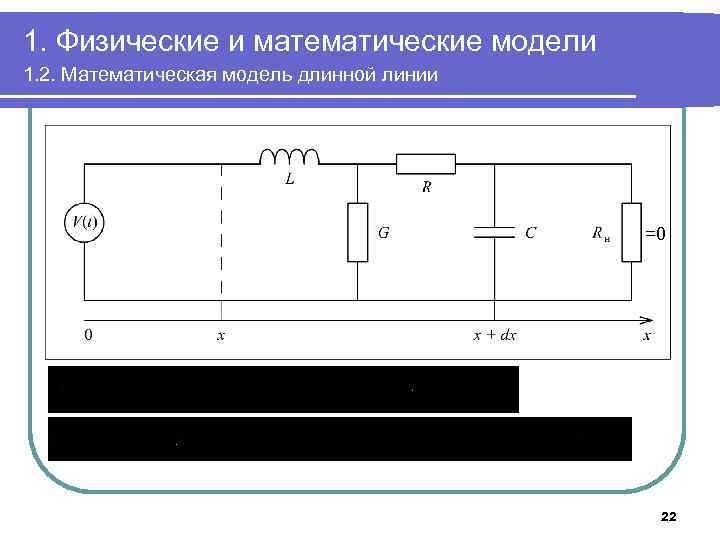 1. Физические и математические модели 1. 2. Математическая модель длинной линии =0 22
1. Физические и математические модели 1. 2. Математическая модель длинной линии =0 22
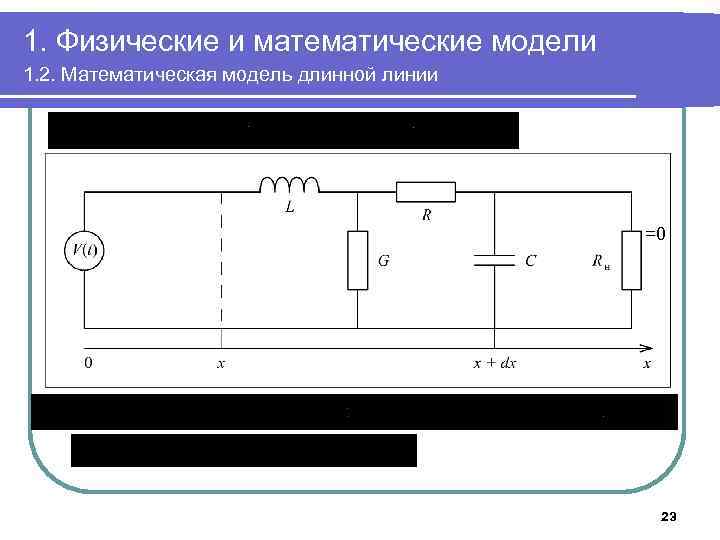 1. Физические и математические модели 1. 2. Математическая модель длинной линии =0 23
1. Физические и математические модели 1. 2. Математическая модель длинной линии =0 23
 1. Физические и математические модели 1. 2. Математическая модель длинной линии 24
1. Физические и математические модели 1. 2. Математическая модель длинной линии 24
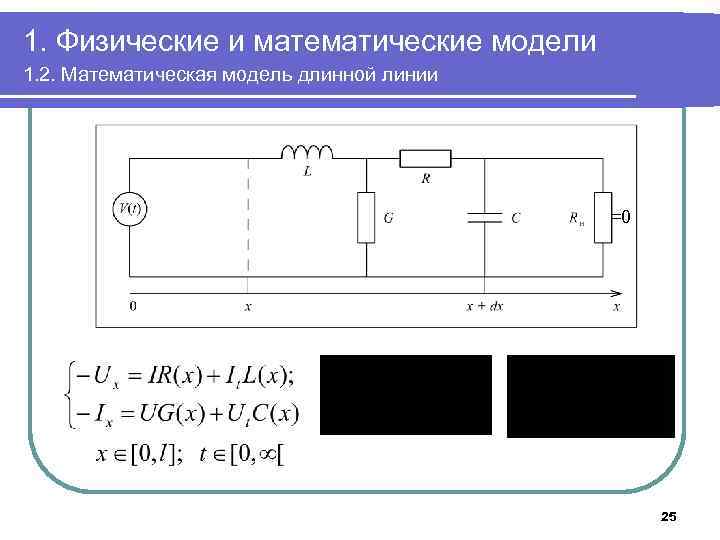 1. Физические и математические модели 1. 2. Математическая модель длинной линии =0 25
1. Физические и математические модели 1. 2. Математическая модель длинной линии =0 25
 1. Физические и математические модели 1. 2. Математическая модель длинной линии 26
1. Физические и математические модели 1. 2. Математическая модель длинной линии 26
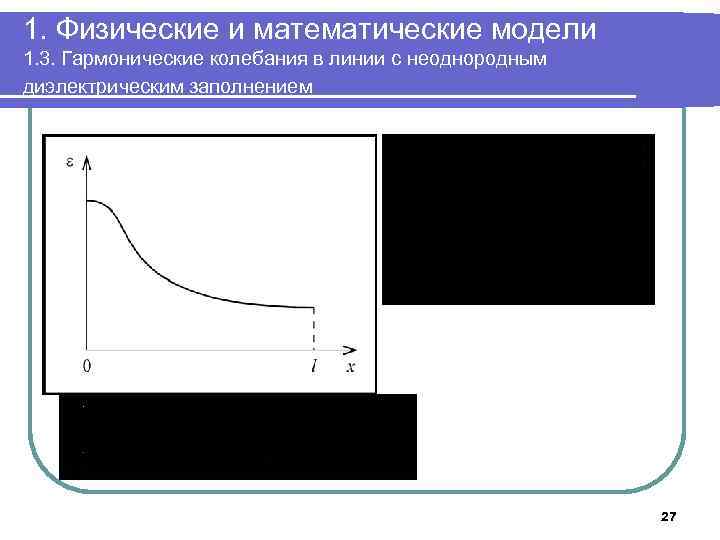 1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 27
1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 27
 1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 28
1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 28
 1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 29
1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 29
 1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 30
1. Физические и математические модели 1. 3. Гармонические колебания в линии с неоднородным диэлектрическим заполнением 30
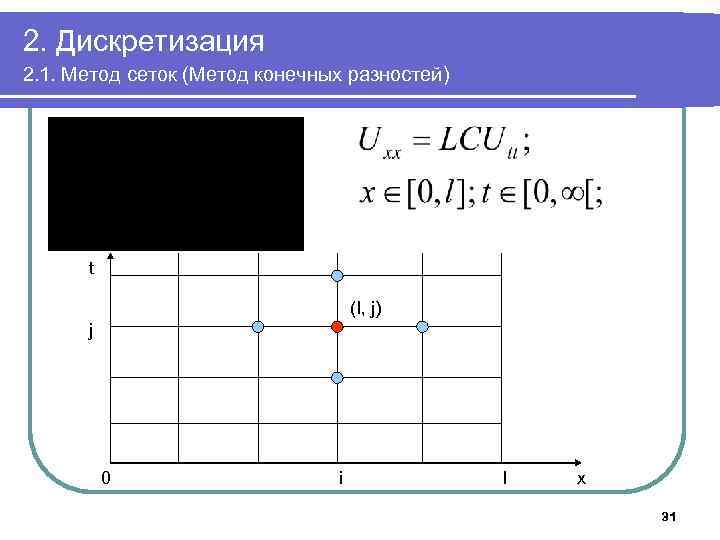 2. Дискретизация 2. 1. Метод сеток (Метод конечных разностей) t (I, j) j 0 i l x 31
2. Дискретизация 2. 1. Метод сеток (Метод конечных разностей) t (I, j) j 0 i l x 31
 2. Дискретизация 2. 2. Проекционные методы 32
2. Дискретизация 2. 2. Проекционные методы 32
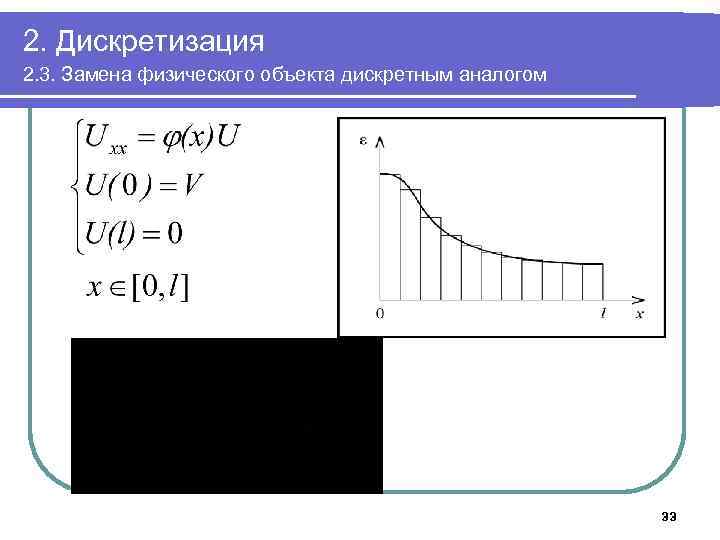 2. Дискретизация 2. 3. Замена физического объекта дискретным аналогом 33
2. Дискретизация 2. 3. Замена физического объекта дискретным аналогом 33
 3. Метод сеток 3. 1. Аппроксимация производных h=l/n x 0 X=0 x 1 … xk-1 xk xk+1 … xn x X=l 34
3. Метод сеток 3. 1. Аппроксимация производных h=l/n x 0 X=0 x 1 … xk-1 xk xk+1 … xn x X=l 34
 3. Метод сеток 3. 1. Аппроксимация производных 35
3. Метод сеток 3. 1. Аппроксимация производных 35
 3. Метод сеток 3. 1. Аппроксимация производных 36
3. Метод сеток 3. 1. Аппроксимация производных 36
 3. Метод сеток 3. 1. Аппроксимация производных - 37
3. Метод сеток 3. 1. Аппроксимация производных - 37
 3. Метод сеток 3. 1. Аппроксимация производных 38
3. Метод сеток 3. 1. Аппроксимация производных 38
 3. Метод сеток 3. 1. Аппроксимация производных 39
3. Метод сеток 3. 1. Аппроксимация производных 39
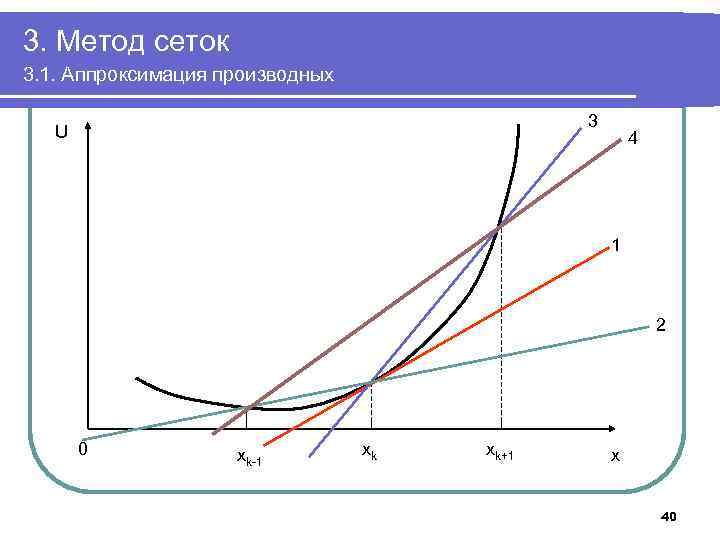 3. Метод сеток 3. 1. Аппроксимация производных 3 U 4 1 2 0 xk-1 xk xk+1 x 40
3. Метод сеток 3. 1. Аппроксимация производных 3 U 4 1 2 0 xk-1 xk xk+1 x 40
 3. Метод сеток 3. 1. Аппроксимация производных + 41
3. Метод сеток 3. 1. Аппроксимация производных + 41
 3. Метод сеток 3. 1. Аппроксимация производных 42
3. Метод сеток 3. 1. Аппроксимация производных 42
 3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток h=l/n x 0 X=0 x 1 … xk-1 xk xk+1 … xn x X=l 43
3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток h=l/n x 0 X=0 x 1 … xk-1 xk xk+1 … xn x X=l 43
 3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток h=l/n x 0 X=0 x 1 … xk-1 xk xk+1 … xn x X=l 44
3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток h=l/n x 0 X=0 x 1 … xk-1 xk xk+1 … xn x X=l 44
 3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток 45
3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток 45
 3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток 46
3. Метод сеток 3. 2. Решение краевой задачи для ОДУ методом сеток 46
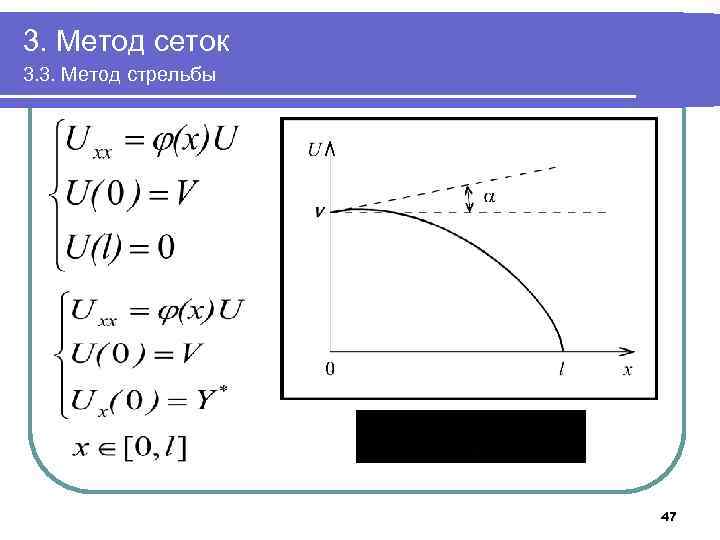 3. Метод сеток 3. 3. Метод стрельбы 47
3. Метод сеток 3. 3. Метод стрельбы 47
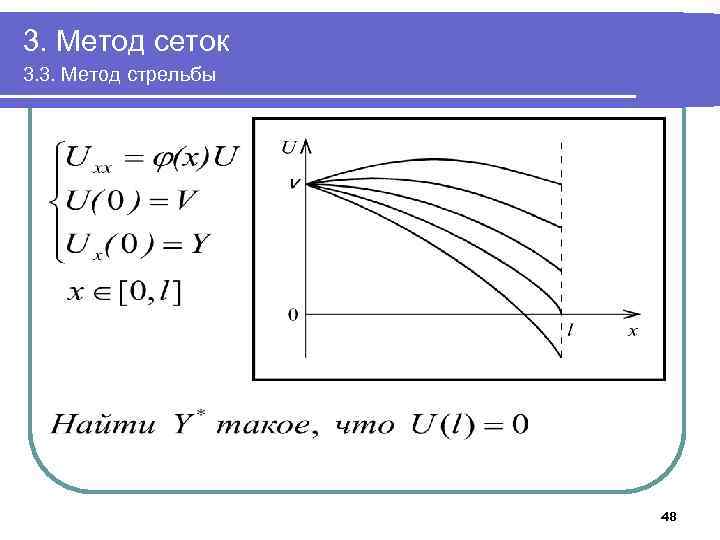 3. Метод сеток 3. 3. Метод стрельбы 48
3. Метод сеток 3. 3. Метод стрельбы 48
 3. Метод сеток 3. 3. Метод стрельбы Алгоритм метода стрельбы сводится к численному решению относительно Y нелинейного уравнения при этом значения функции U вычисляются путем численного решения задачи 49
3. Метод сеток 3. 3. Метод стрельбы Алгоритм метода стрельбы сводится к численному решению относительно Y нелинейного уравнения при этом значения функции U вычисляются путем численного решения задачи 49
 3. Метод сеток 3. 3. Метод стрельбы Найдя решение нелинейного уравнения Y=Y*, автоматически получают приближенное решение исходной задачи, так как решения задач совпадают (разумеется, с некоторой точностью, определяемой точностью решения нелинейного уравнения и точностью численного интегрирования 50
3. Метод сеток 3. 3. Метод стрельбы Найдя решение нелинейного уравнения Y=Y*, автоматически получают приближенное решение исходной задачи, так как решения задач совпадают (разумеется, с некоторой точностью, определяемой точностью решения нелинейного уравнения и точностью численного интегрирования 50
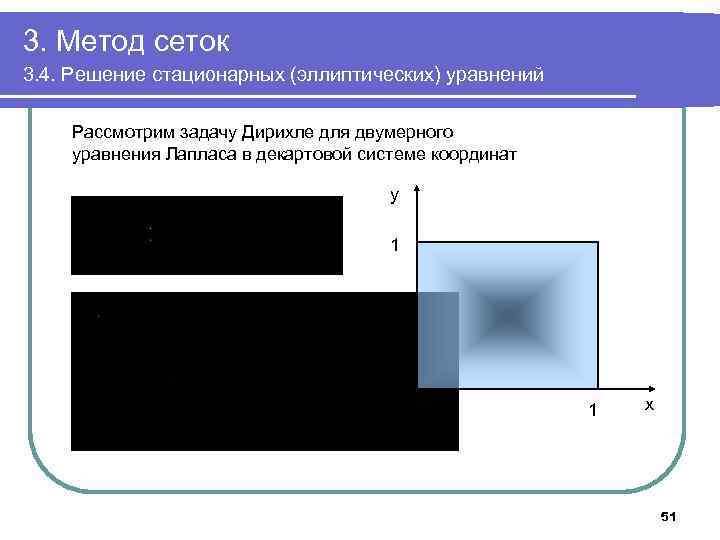 3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений Рассмотрим задачу Дирихле для двумерного уравнения Лапласа в декартовой системе координат y 1 1 х 51
3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений Рассмотрим задачу Дирихле для двумерного уравнения Лапласа в декартовой системе координат y 1 1 х 51
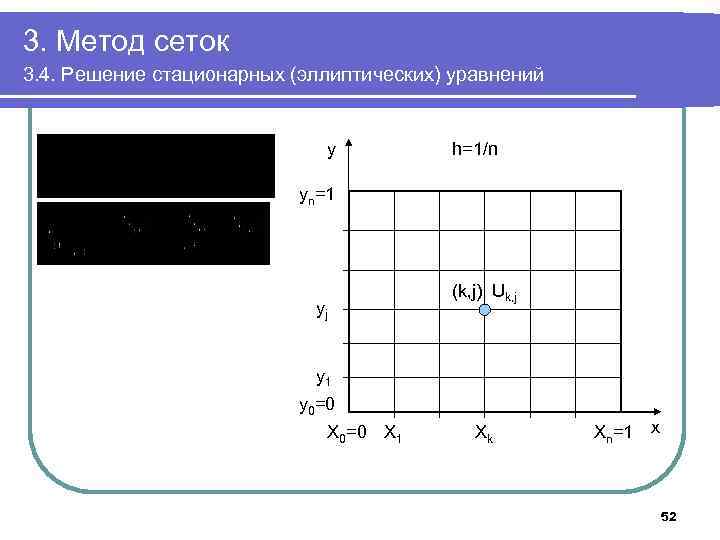 3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений y h=1/n yn=1 yj (k, j) Uk, j y 1 y 0=0 Х 1 Хk Хn=1 х 52
3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений y h=1/n yn=1 yj (k, j) Uk, j y 1 y 0=0 Х 1 Хk Хn=1 х 52
 3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений 53
3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений 53
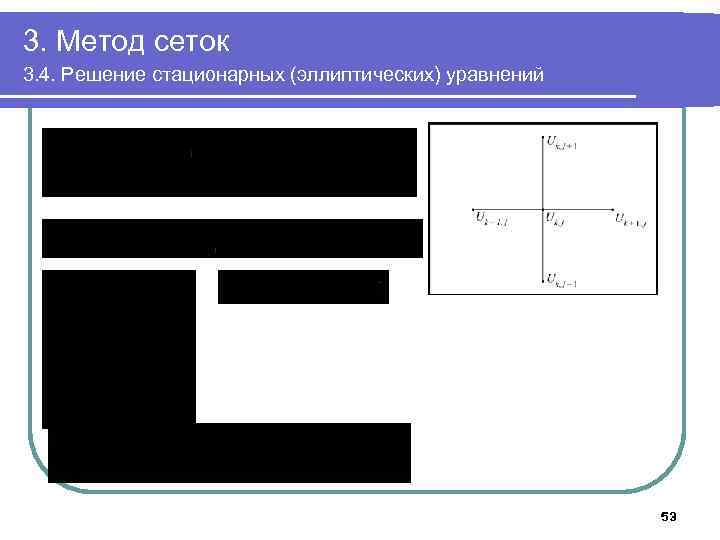
 3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений Разностное уравнение – уравнение, полученное путем замены производных в исходном ДУ конечно-разностными аппроксимациями Вычислительный шаблон – совокупность узлов сетки, участвующих в аппроксимации производных в одном из узлов Разностная схема – разностное уравнение + дискретные аналоги граничных (и начальных) условий 54
3. Метод сеток 3. 4. Решение стационарных (эллиптических) уравнений Разностное уравнение – уравнение, полученное путем замены производных в исходном ДУ конечно-разностными аппроксимациями Вычислительный шаблон – совокупность узлов сетки, участвующих в аппроксимации производных в одном из узлов Разностная схема – разностное уравнение + дискретные аналоги граничных (и начальных) условий 54
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Обозначим Ukj (s) - приближенное значение функции на s-й итерации в узле (k, j). Ukj (0) - начальное приближение в этом узле. Метод Якоби (метод одновременных смещений): Начальные значения на 0 -й итерации: 55
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Обозначим Ukj (s) - приближенное значение функции на s-й итерации в узле (k, j). Ukj (0) - начальное приближение в этом узле. Метод Якоби (метод одновременных смещений): Начальные значения на 0 -й итерации: 55
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 1. Задать n, ε, положить h=1/n. Разместить в памяти массивы Ua[0. . n, 0. . n], Ub[0. . n, 0. . n]. 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; Ua[0, i]: =g(0, y); Ua[n, i]: =g(1, y); Ua[i, 0]: =g(x, 0); Ua[i, 1]: =g(x, 1); Ub[0, i]: =g(0, y); Ub[n, i]: =g(1, y); Ub[i, 0]: =g(x, 0); Ub[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить Ua[k, j]: =v 56
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 1. Задать n, ε, положить h=1/n. Разместить в памяти массивы Ua[0. . n, 0. . n], Ub[0. . n, 0. . n]. 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; Ua[0, i]: =g(0, y); Ua[n, i]: =g(1, y); Ua[i, 0]: =g(x, 0); Ua[i, 1]: =g(x, 1); Ub[0, i]: =g(0, y); Ub[n, i]: =g(1, y); Ub[i, 0]: =g(x, 0); Ub[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить Ua[k, j]: =v 56
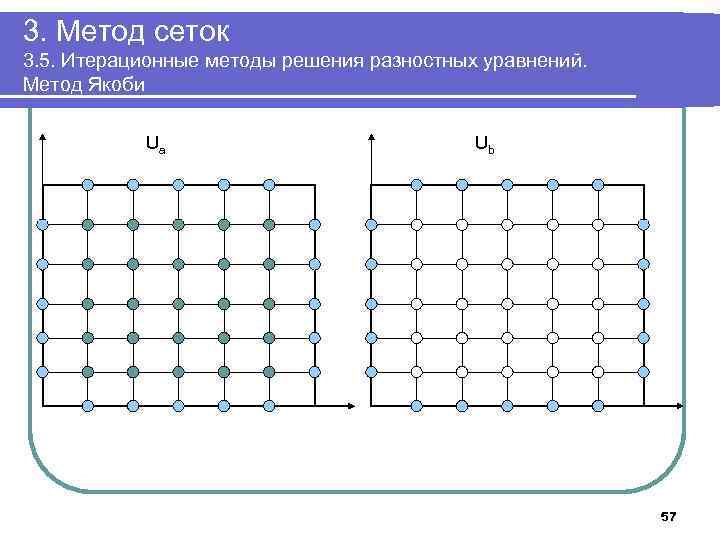 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 57
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 57
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 1. Задать n, ε, положить h=1/n. Разместить в памяти массивы Ua[0. . n, 0. . n], Ub[0. . n, 0. . n]. 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; Ua[0, i]: =g(0, y); Ua[n, i]: =g(1, y); Ua[i, 0]: =g(x, 0); Ua[i, 1]: =g(x, 1); Ub[0, i]: =g(0, y); Ub[n, i]: =g(1, y); Ub[i, 0]: =g(x, 0); Ub[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить Ua[k, j]: =v 58
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 1. Задать n, ε, положить h=1/n. Разместить в памяти массивы Ua[0. . n, 0. . n], Ub[0. . n, 0. . n]. 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; Ua[0, i]: =g(0, y); Ua[n, i]: =g(1, y); Ua[i, 0]: =g(x, 0); Ua[i, 1]: =g(x, 1); Ub[0, i]: =g(0, y); Ub[n, i]: =g(1, y); Ub[i, 0]: =g(x, 0); Ub[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить Ua[k, j]: =v 58
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 6. Выполнять в цикле Положить δ: =0; Для k=1. . n-1, j=1. . n-1 выполнить Ub[k, j]: =(Ua[k-1, j]+ Ua[k+1, j]+Ua[k, j-1]+ Ua[k, j+1])/4; Для k=1. . n-1, j=1. . n-1 выполнить Ua[k, j]: =(Ub[k-1, j]+ Ub[k+1, j]+Ub[k, , j-1]+ Ub[k, , j+1])/4. Если δ<| Ua[k, j]-Ub[k, j]|, положить δ: =| Ua[k, j]-Ub[k, j]| До тех пор, пока δ> ε 7. Вывести массив Ua 8. Завершить работу 59
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 6. Выполнять в цикле Положить δ: =0; Для k=1. . n-1, j=1. . n-1 выполнить Ub[k, j]: =(Ua[k-1, j]+ Ua[k+1, j]+Ua[k, j-1]+ Ua[k, j+1])/4; Для k=1. . n-1, j=1. . n-1 выполнить Ua[k, j]: =(Ub[k-1, j]+ Ub[k+1, j]+Ub[k, , j-1]+ Ub[k, , j+1])/4. Если δ<| Ua[k, j]-Ub[k, j]|, положить δ: =| Ua[k, j]-Ub[k, j]| До тех пор, пока δ> ε 7. Вывести массив Ua 8. Завершить работу 59
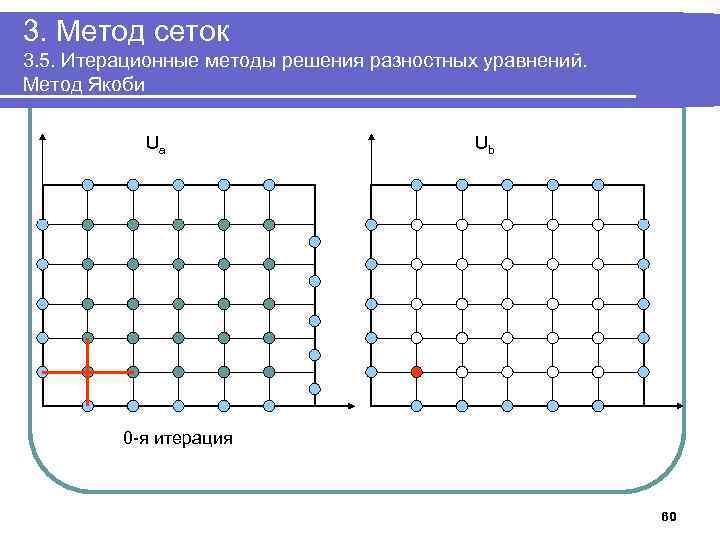 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 0 -я итерация 60
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 0 -я итерация 60
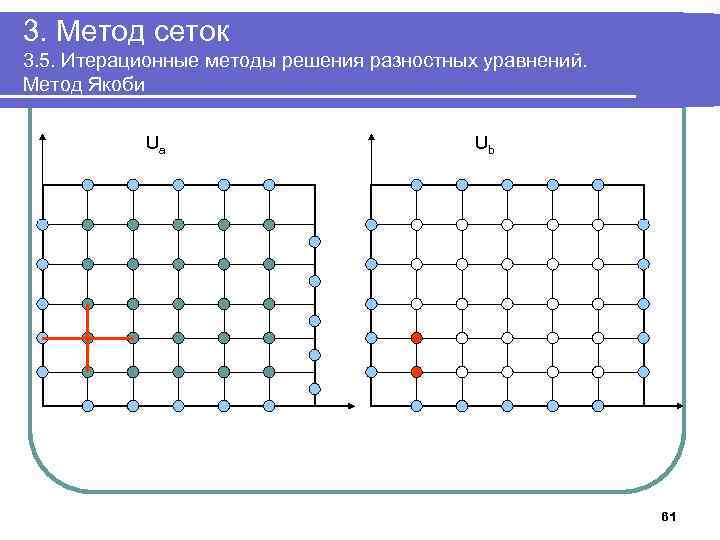 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 61
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 61
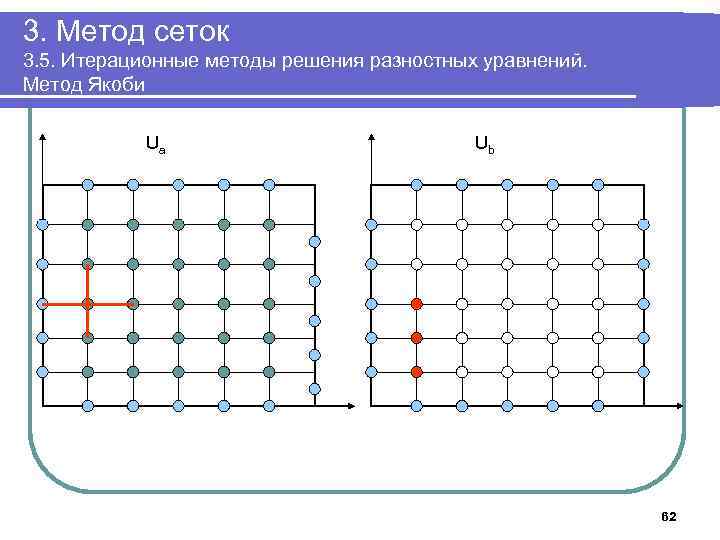 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 62
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 62
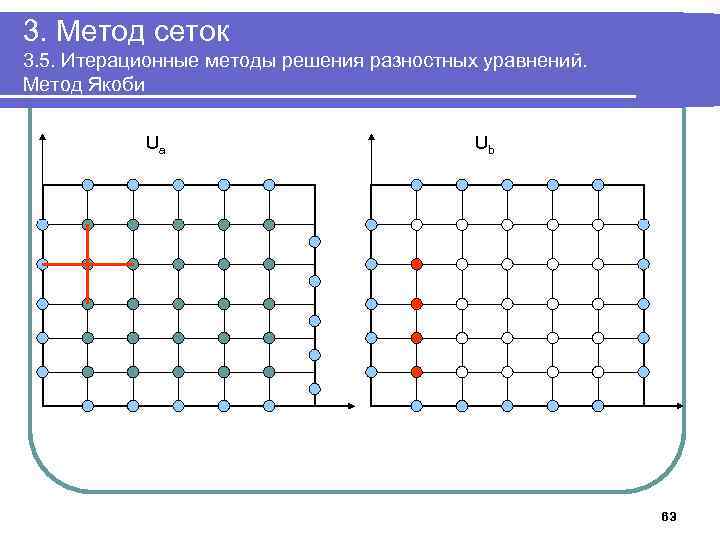 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 63
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 63
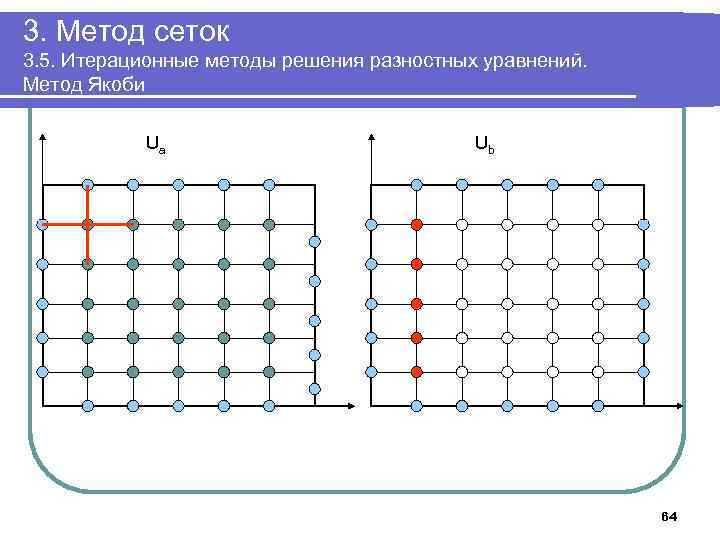 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 64
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 64
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 65
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 65
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 66
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 66
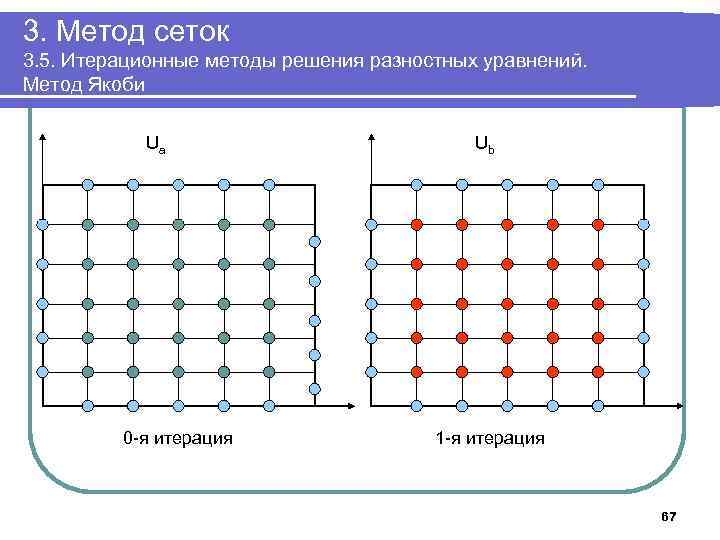 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua 0 -я итерация Ub 1 -я итерация 67
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua 0 -я итерация Ub 1 -я итерация 67
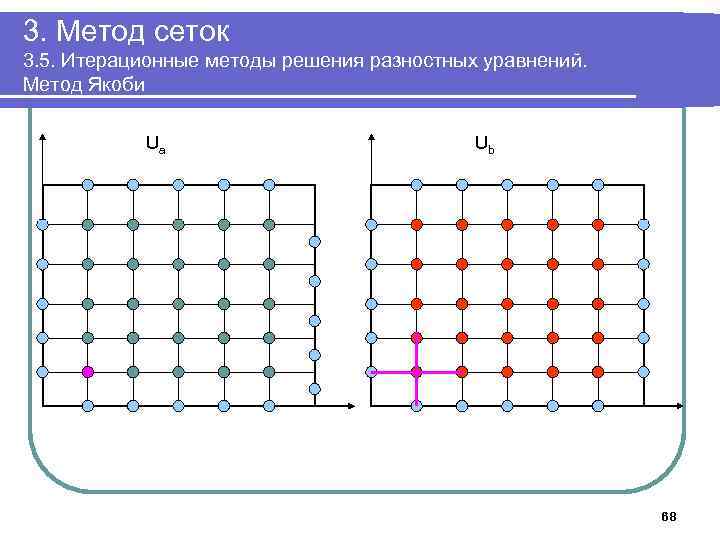 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 68
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 68
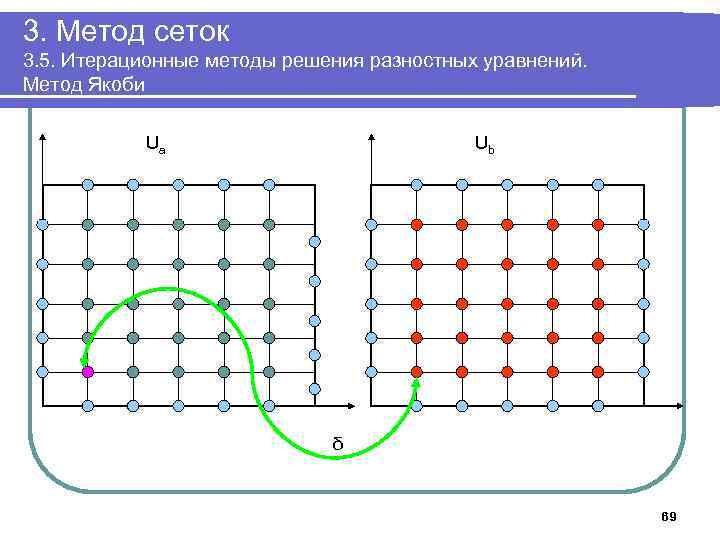 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub δ 69
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub δ 69
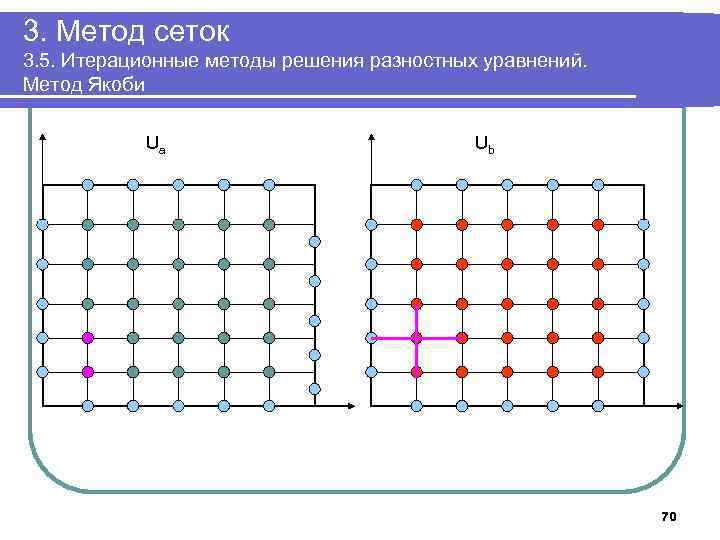 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 70
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua Ub 70
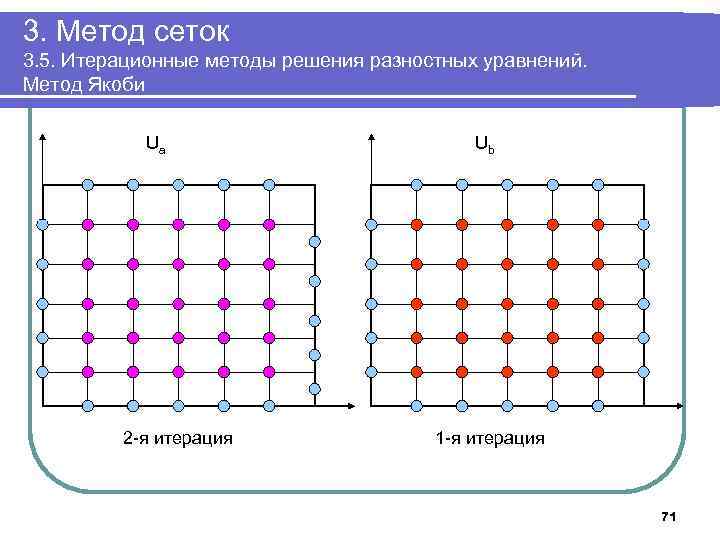 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua 2 -я итерация Ub 1 -я итерация 71
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби Ua 2 -я итерация Ub 1 -я итерация 71
 3. Метод сеток 3. 6. Итерационные методы решения разностных уравнений. Метод Либмана Обозначим Ukj (s) - приближенное значение функции на s-й итерации в узле (k, j). Ukj (0) - начальное приближение в этом узле. Метод Либмана (метод последовательных смещений): Начальные значения на 0 -й итерации: 72
3. Метод сеток 3. 6. Итерационные методы решения разностных уравнений. Метод Либмана Обозначим Ukj (s) - приближенное значение функции на s-й итерации в узле (k, j). Ukj (0) - начальное приближение в этом узле. Метод Либмана (метод последовательных смещений): Начальные значения на 0 -й итерации: 72
 3. Метод сеток 3. 6. Итерационные методы решения разностных уравнений. Метод Либмана 1. Задать n, ε, положить h=1/n. Разместить в памяти массив U[0. . n, 0. . n], 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; U[0, i]: =g(0, y); U[n, i]: =g(1, y); U[i, 0]: =g(x, 0); U[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить U[k, j]: =v 73
3. Метод сеток 3. 6. Итерационные методы решения разностных уравнений. Метод Либмана 1. Задать n, ε, положить h=1/n. Разместить в памяти массив U[0. . n, 0. . n], 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; U[0, i]: =g(0, y); U[n, i]: =g(1, y); U[i, 0]: =g(x, 0); U[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить U[k, j]: =v 73
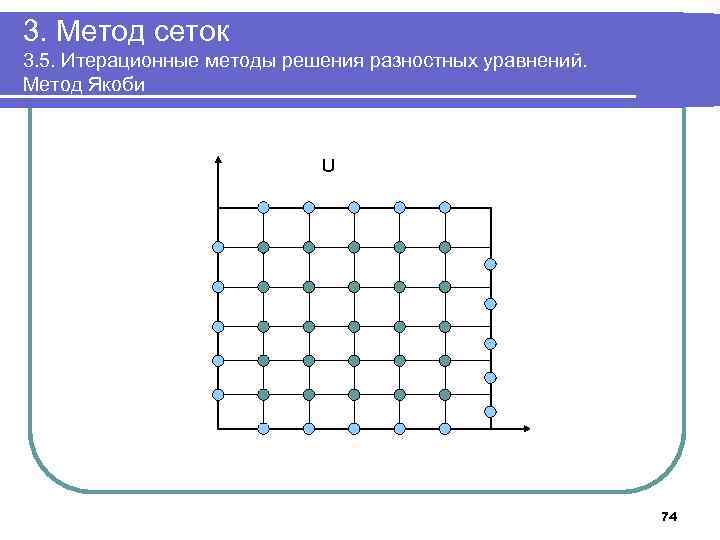 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 74
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 74
 3. Метод сеток 3. 6. Итерационные методы решения разностных уравнений. Метод Либмана 1. Задать n, ε, положить h=1/n. Разместить в памяти массив U[0. . n, 0. . n], 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; U[0, i]: =g(0, y); U[n, i]: =g(1, y); U[i, 0]: =g(x, 0); U[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить U[k, j]: =v 75
3. Метод сеток 3. 6. Итерационные методы решения разностных уравнений. Метод Либмана 1. Задать n, ε, положить h=1/n. Разместить в памяти массив U[0. . n, 0. . n], 2. Положить v: =0; 3. Для i=1. . n-1 выполнить x: =i*h; y: =i*h; U[0, i]: =g(0, y); U[n, i]: =g(1, y); U[i, 0]: =g(x, 0); U[i, 1]: =g(x, 1); v: =v+g(0, y)+g(1, y)+g(x, 0)+g(x, 1); 4. Положить v: = v/4/(n-1) 5. Для k=1. . n-1, j=1. . n-1 выполнить U[k, j]: =v 75
 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 6. Выполнять в цикле Положить δ: =0; Для k=1. . n-1, j=1. . n-1 выполнить Положить q: =U[k, j]: =(U[k-1, j]+ U[k+1, j]+U[k, j-1]+ U[k, j+1])/4 Если δ<| U[k, j]-q|, положить δ: =| U [k, j]-q]| До тех пор, пока δ> ε 7. Вывести массив U 8. Завершить работу. 76
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби 6. Выполнять в цикле Положить δ: =0; Для k=1. . n-1, j=1. . n-1 выполнить Положить q: =U[k, j]: =(U[k-1, j]+ U[k+1, j]+U[k, j-1]+ U[k, j+1])/4 Если δ<| U[k, j]-q|, положить δ: =| U [k, j]-q]| До тех пор, пока δ> ε 7. Вывести массив U 8. Завершить работу. 76
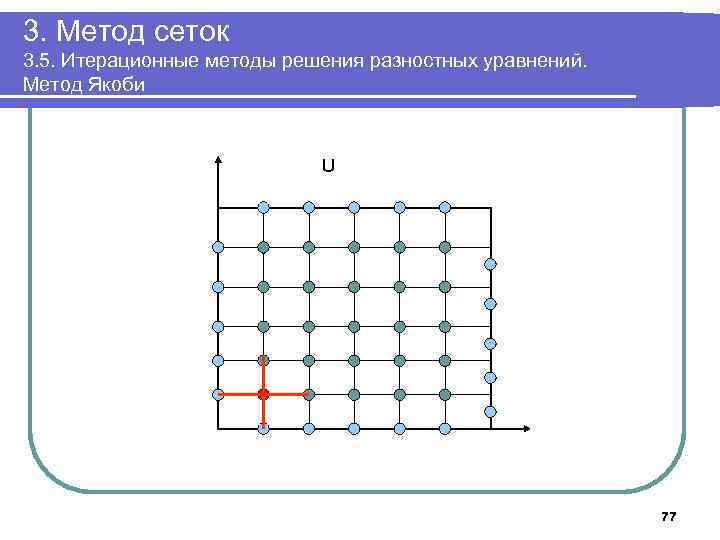 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 77
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 77
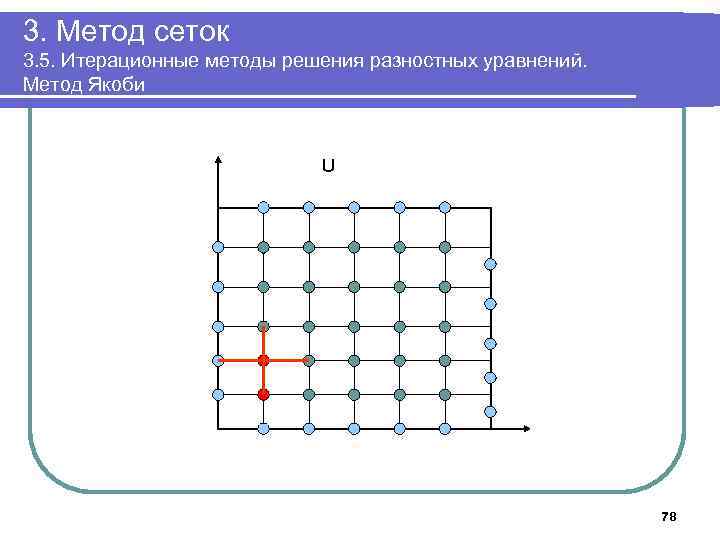 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 78
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 78
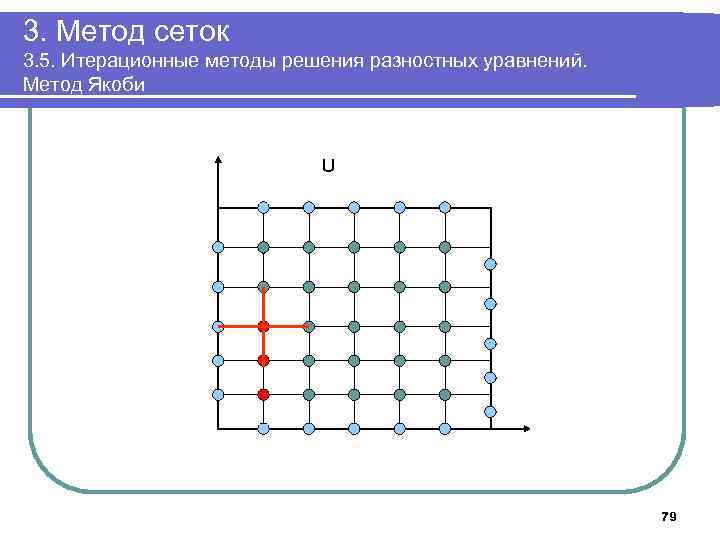 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 79
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 79
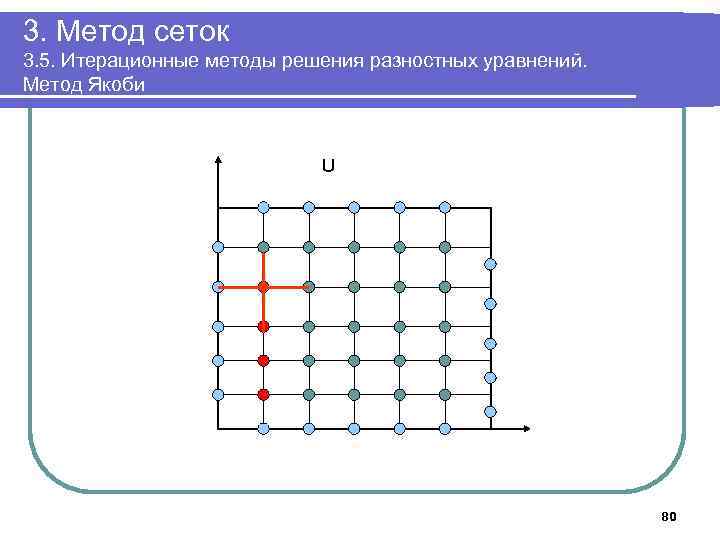 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 80
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 80
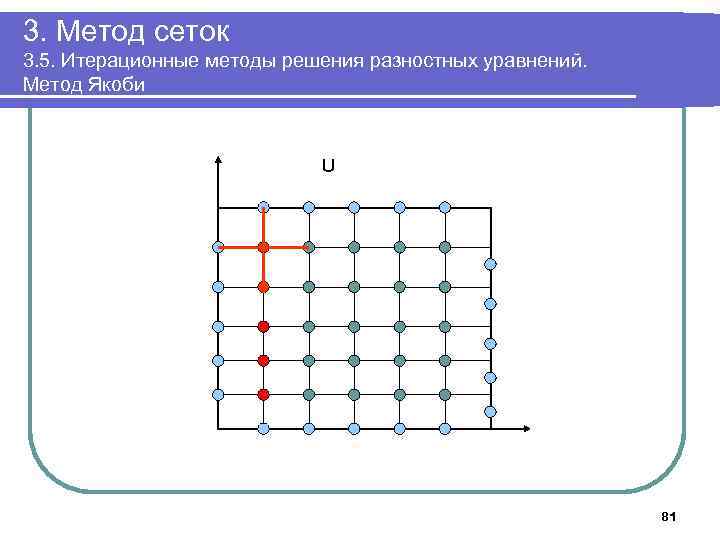 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 81
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 81
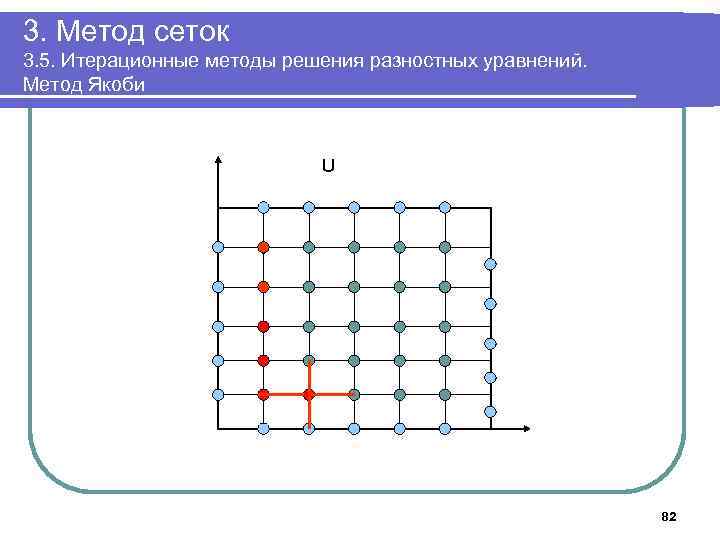 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 82
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 82
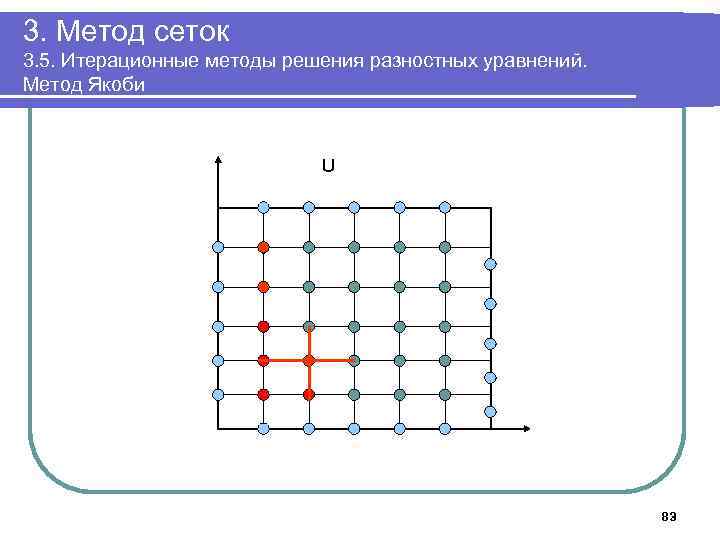 3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 83
3. Метод сеток 3. 5. Итерационные методы решения разностных уравнений. Метод Якоби U 83
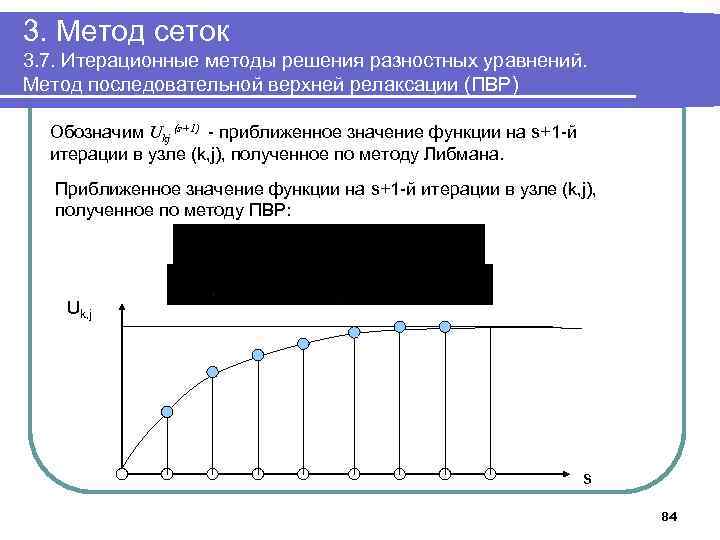 3. Метод сеток 3. 7. Итерационные методы решения разностных уравнений. Метод последовательной верхней релаксации (ПВР) Обозначим Ukj (s+1) - приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу Либмана. Приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу ПВР: Uk, j s 84
3. Метод сеток 3. 7. Итерационные методы решения разностных уравнений. Метод последовательной верхней релаксации (ПВР) Обозначим Ukj (s+1) - приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу Либмана. Приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу ПВР: Uk, j s 84
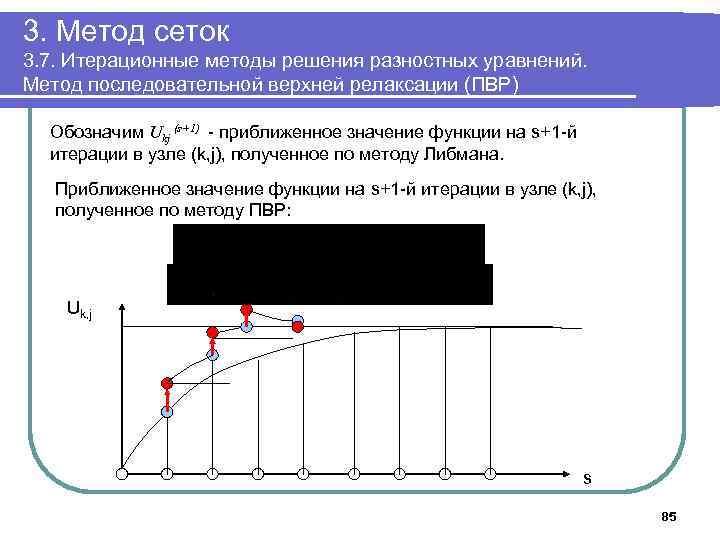 3. Метод сеток 3. 7. Итерационные методы решения разностных уравнений. Метод последовательной верхней релаксации (ПВР) Обозначим Ukj (s+1) - приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу Либмана. Приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу ПВР: Uk, j s 85
3. Метод сеток 3. 7. Итерационные методы решения разностных уравнений. Метод последовательной верхней релаксации (ПВР) Обозначим Ukj (s+1) - приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу Либмана. Приближенное значение функции на s+1 -й итерации в узле (k, j), полученное по методу ПВР: Uk, j s 85
 3. Метод сеток 3. 7. Экстраполяция по Ричардсону 86
3. Метод сеток 3. 7. Экстраполяция по Ричардсону 86
 3. Метод сеток 3. 8. Неоднородное стационарное уравнение и область решения произвольной формы y х 87
3. Метод сеток 3. 8. Неоднородное стационарное уравнение и область решения произвольной формы y х 87
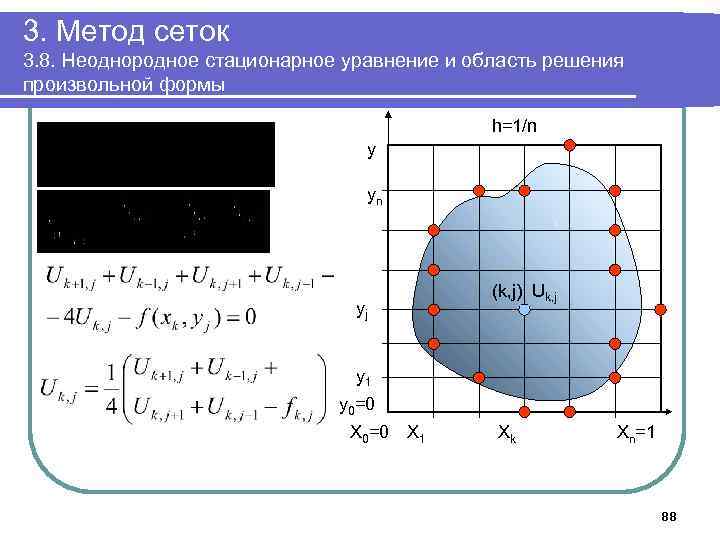 3. Метод сеток 3. 8. Неоднородное стационарное уравнение и область решения произвольной формы h=1/n y yn yj (k, j) Uk, j y 1 y 0=0 Х 1 Хk Хn=1 88
3. Метод сеток 3. 8. Неоднородное стационарное уравнение и область решения произвольной формы h=1/n y yn yj (k, j) Uk, j y 1 y 0=0 Х 1 Хk Хn=1 88
 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности t x 89
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности t x 89
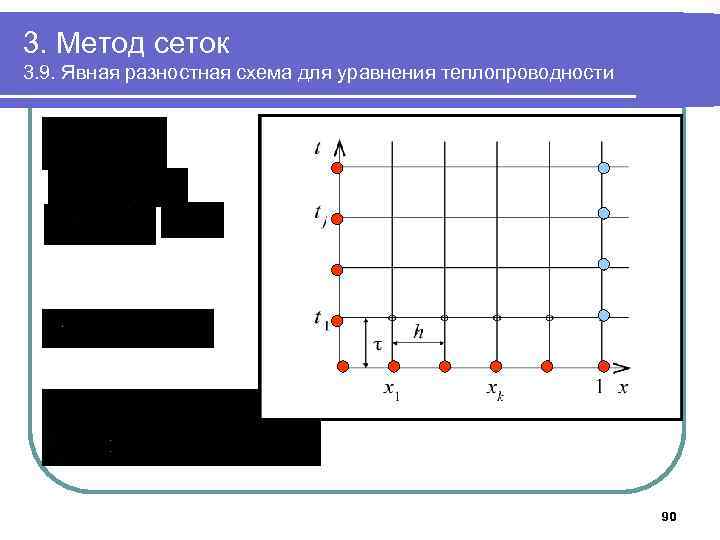 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 90
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 90
 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 91
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 91
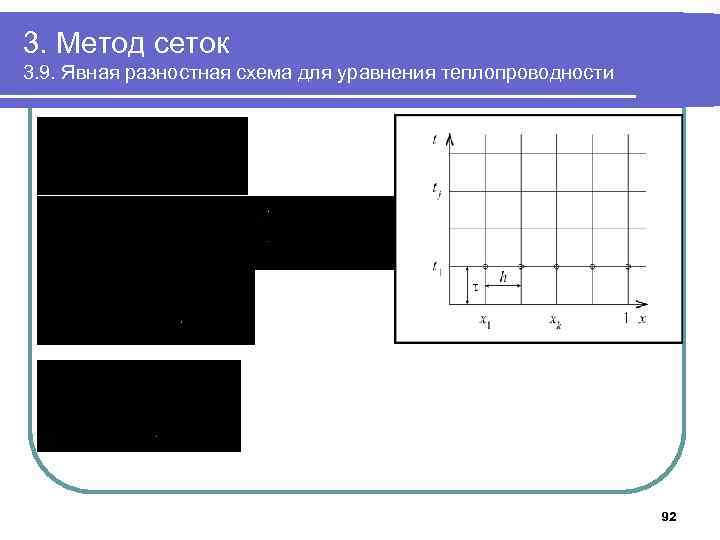 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 92
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 92
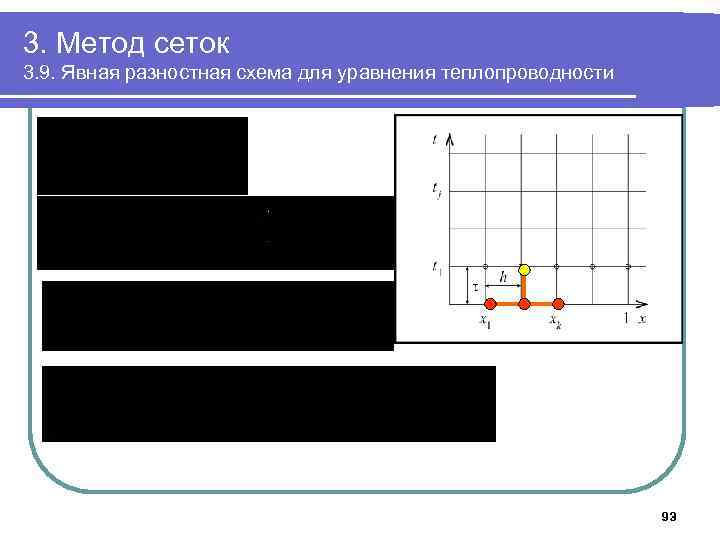 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 93
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 93
 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 94
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 94
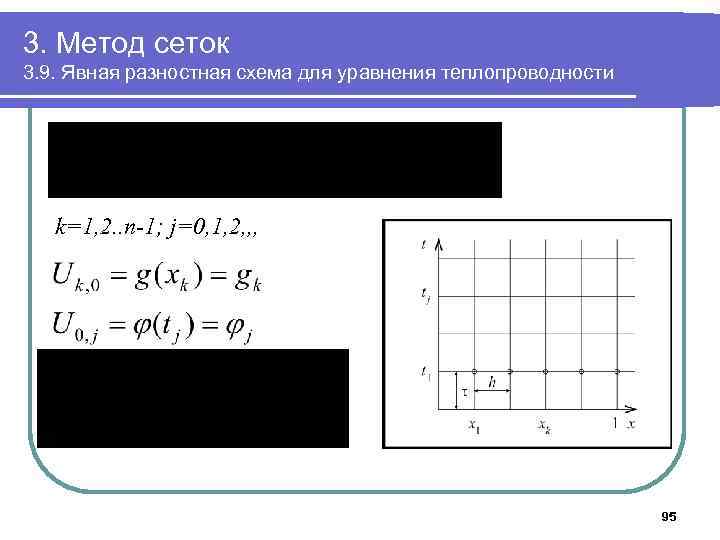 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности k=1, 2. . n-1; j=0, 1, 2, , , 95
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности k=1, 2. . n-1; j=0, 1, 2, , , 95
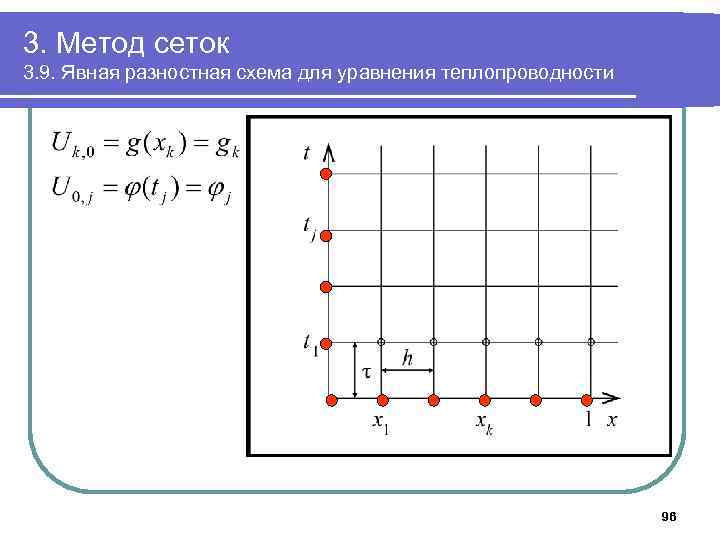 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 96
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 96
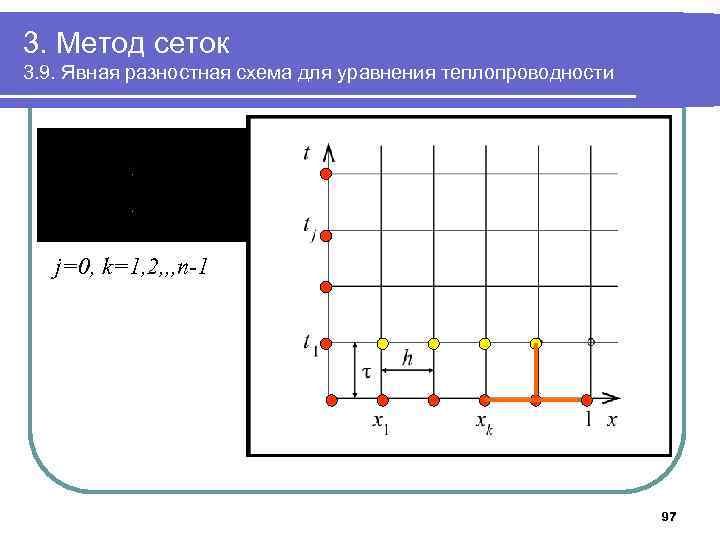 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности j=0, k=1, 2, , , n-1 97
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности j=0, k=1, 2, , , n-1 97
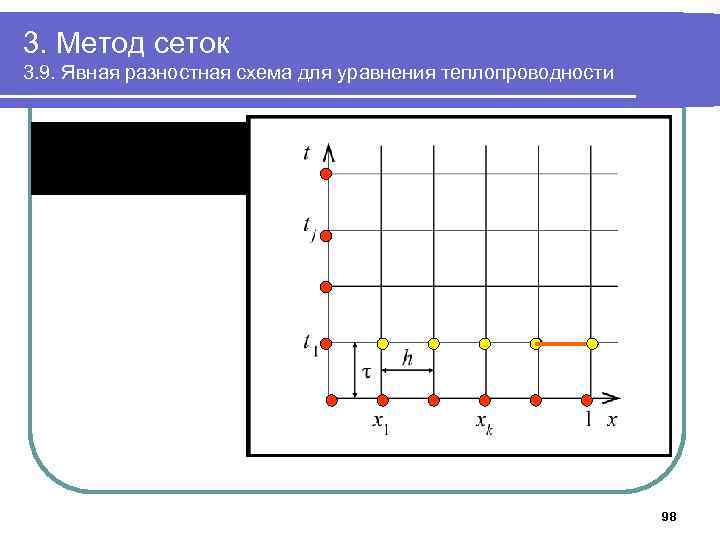 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 98
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 98
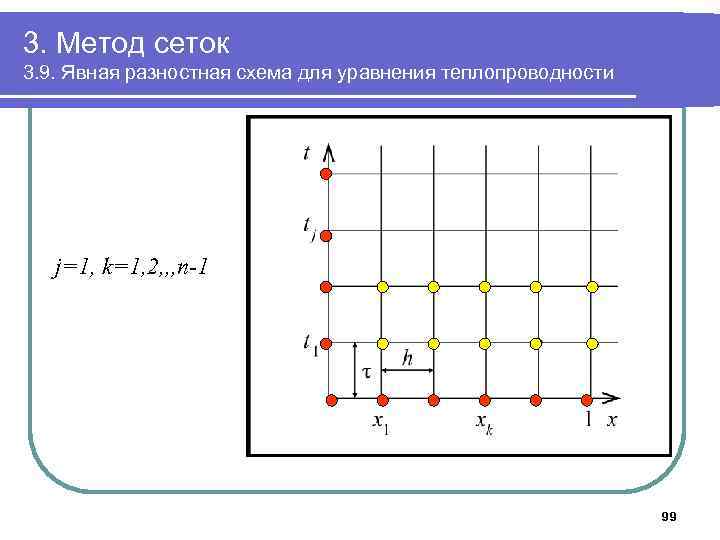 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности j=1, k=1, 2, , , n-1 99
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности j=1, k=1, 2, , , n-1 99
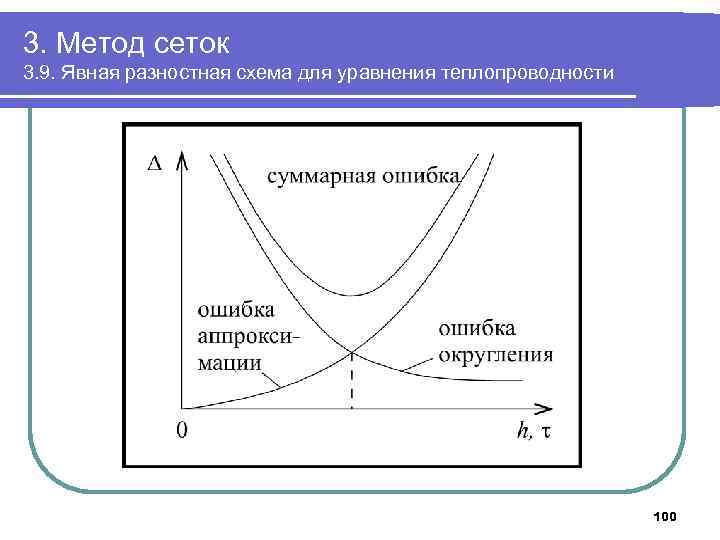 3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 100
3. Метод сеток 3. 9. Явная разностная схема для уравнения теплопроводности 100
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 101
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 101
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 102
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 102
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 103
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 103
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 104
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 104
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 105
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость 105
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Разностная схема называется корректной, если: 1. её решение существует и оно единственно при любых ограниченных правых частях. 2. такое m > 0, m m(h), что для любой 106
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Разностная схема называется корректной, если: 1. её решение существует и оно единственно при любых ограниченных правых частях. 2. такое m > 0, m m(h), что для любой 106
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Теорема: Пусть исходная задача поставлена корректно, разностная схема корректна, и аппроксимирует исходную задачу. Тогда решение разностной задачи сходится к решению исходной задачи (1), причём порядок малости погрешности совпадает с порядком аппроксимации (2). 107
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Теорема: Пусть исходная задача поставлена корректно, разностная схема корректна, и аппроксимирует исходную задачу. Тогда решение разностной задачи сходится к решению исходной задачи (1), причём порядок малости погрешности совпадает с порядком аппроксимации (2). 107
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Доказательство (1): 108
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Доказательство (1): 108
 3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Доказательство (2): 109
3. Метод сеток 3. 10. Аппроксимация, устойчивость, сходимость Доказательство (2): 109
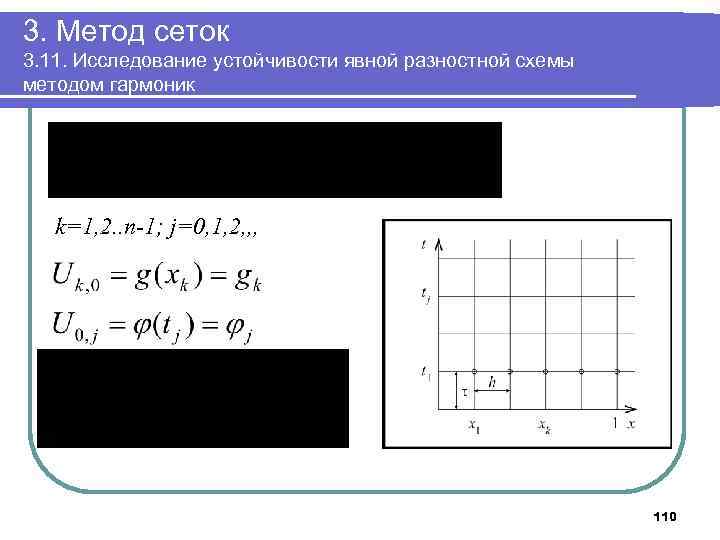 3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник k=1, 2. . n-1; j=0, 1, 2, , , 110
3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник k=1, 2. . n-1; j=0, 1, 2, , , 110
 3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник 111
3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник 111
 3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник Условие устойчивости: |ql| 1. 112
3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник Условие устойчивости: |ql| 1. 112
 3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник 113
3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник 113
 3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник 114
3. Метод сеток 3. 11. Исследование устойчивости явной разностной схемы методом гармоник 114
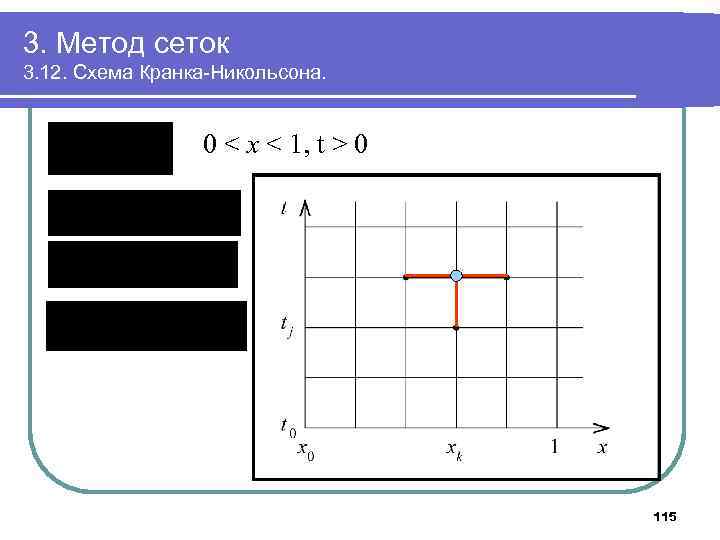 3. Метод сеток 3. 12. Схема Кранка-Никольсона. 0 < x < 1, t > 0 115
3. Метод сеток 3. 12. Схема Кранка-Никольсона. 0 < x < 1, t > 0 115
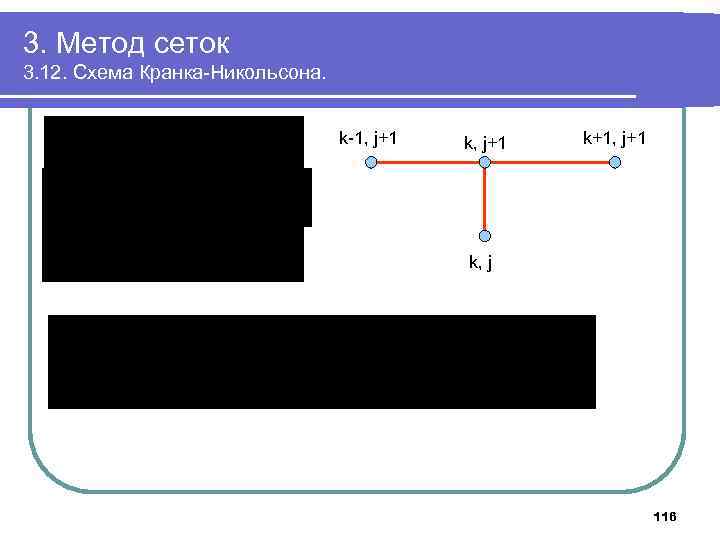 3. Метод сеток 3. 12. Схема Кранка-Никольсона. k-1, j+1 k+1, j+1 k, j 116
3. Метод сеток 3. 12. Схема Кранка-Никольсона. k-1, j+1 k+1, j+1 k, j 116
 3. Метод сеток 3. 12. Схема Кранка-Никольсона. 117
3. Метод сеток 3. 12. Схема Кранка-Никольсона. 117
 3. Метод сеток 3. 12. Схема Кранка-Никольсона. где 0 1 118
3. Метод сеток 3. 12. Схема Кранка-Никольсона. где 0 1 118
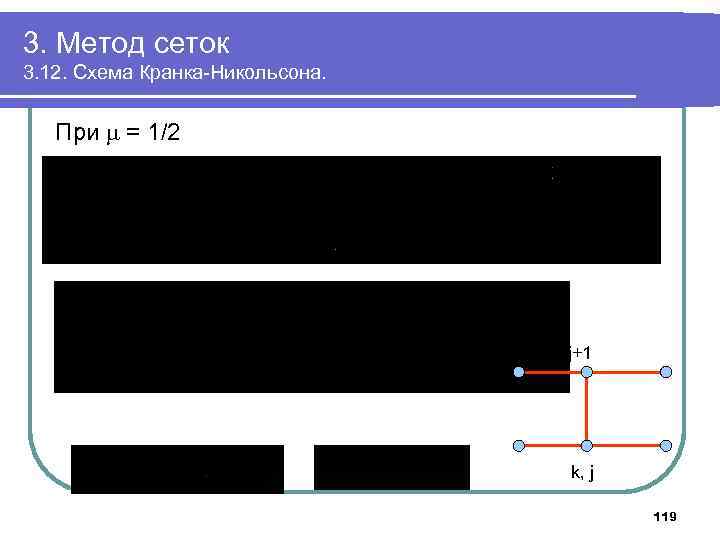 3. Метод сеток 3. 12. Схема Кранка-Никольсона. При = 1/2 k, j+1 k, j 119
3. Метод сеток 3. 12. Схема Кранка-Никольсона. При = 1/2 k, j+1 k, j 119
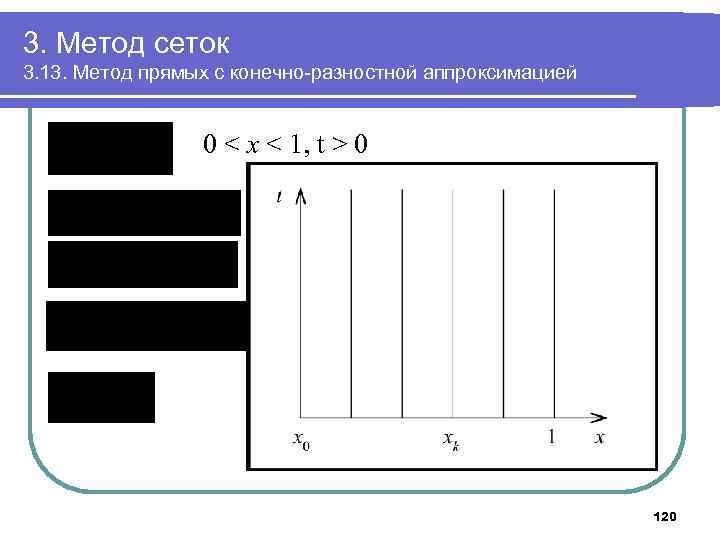 3. Метод сеток 3. 13. Метод прямых с конечно-разностной аппроксимацией 0 < x < 1, t > 0 120
3. Метод сеток 3. 13. Метод прямых с конечно-разностной аппроксимацией 0 < x < 1, t > 0 120
 3. Метод сеток 3. 13. Метод прямых с конечно-разностной аппроксимацией 121
3. Метод сеток 3. 13. Метод прямых с конечно-разностной аппроксимацией 121
 3. Метод сеток 3. 13. Метод прямых с конечно-разностной аппроксимацией 122
3. Метод сеток 3. 13. Метод прямых с конечно-разностной аппроксимацией 122
 4. Проекционные методы 4. 1. Аппроксимация и интерполяция 123
4. Проекционные методы 4. 1. Аппроксимация и интерполяция 123
 4. Проекционные методы 4. 1. Аппроксимация и интерполяция 124
4. Проекционные методы 4. 1. Аппроксимация и интерполяция 124
 4. Проекционные методы 4. 1. Аппроксимация и интерполяция 125
4. Проекционные методы 4. 1. Аппроксимация и интерполяция 125
 4. Проекционные методы 4. 1. Аппроксимация и интерполяция , 126
4. Проекционные методы 4. 1. Аппроксимация и интерполяция , 126
 4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 127
4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 127
 4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 128
4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 128
 4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 129
4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 129
 4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 130
4. Проекционные методы 4. 1. Аппроксимация с помощью взвешенных невязок 130
 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 131
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 131
 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 132
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 132
 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 133
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 133
 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 134
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 134
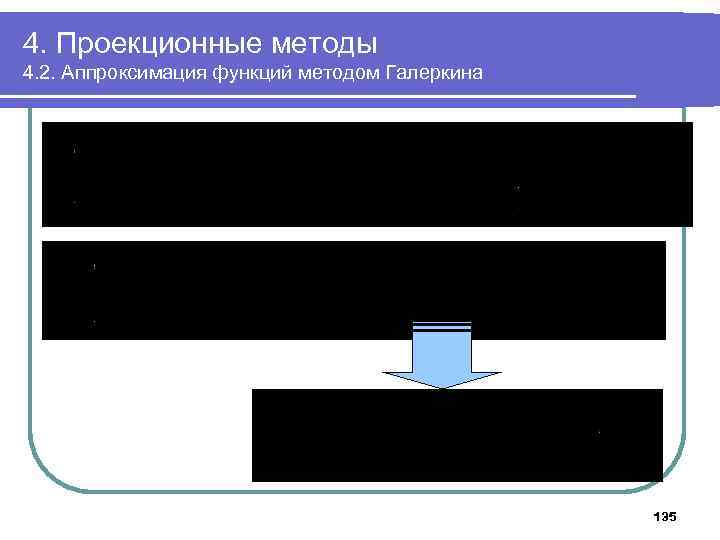 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 135
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 135
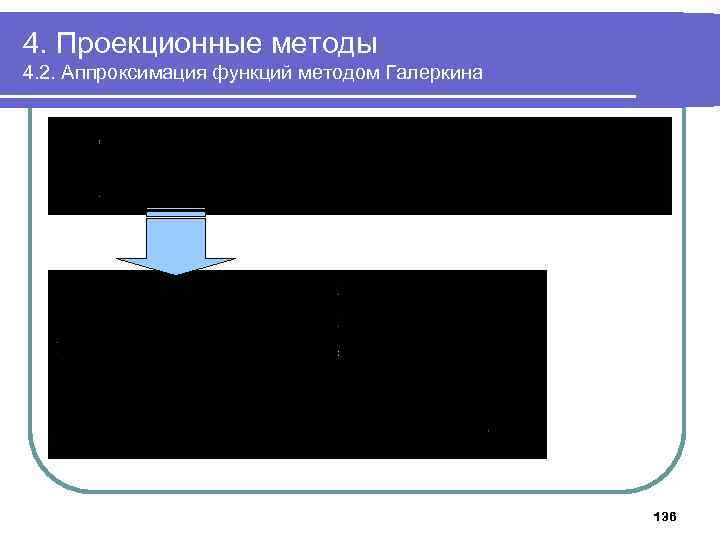 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 136
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 136
 4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 137
4. Проекционные методы 4. 2. Аппроксимация функций методом Галеркина 137
 4. Проекционные методы 4. 3. Аппроксимация функций методом коллокаций 138
4. Проекционные методы 4. 3. Аппроксимация функций методом коллокаций 138
 4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 139
4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 139
 4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 140
4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 140
 4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 141
4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 141
 4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 142
4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 142
 4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 143
4. Проекционные методы 4. 4. Аппроксимация решений дифференциальных уравнений 143
 4. Проекционные методы 4. 5. Кусочные аппроксимации U(x), 0 ≤ x ≤ l в N точках x 1, x 2, …, x. N, U(xj)=Uj. 144
4. Проекционные методы 4. 5. Кусочные аппроксимации U(x), 0 ≤ x ≤ l в N точках x 1, x 2, …, x. N, U(xj)=Uj. 144
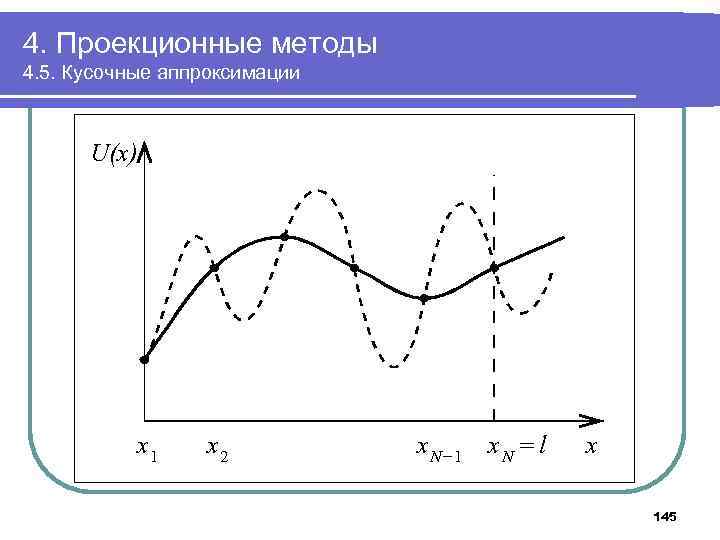 4. Проекционные методы 4. 5. Кусочные аппроксимации U(x) x 1 x 2 x N - 1 x l = N x 145
4. Проекционные методы 4. 5. Кусочные аппроксимации U(x) x 1 x 2 x N - 1 x l = N x 145
 4. Проекционные методы 4. 5. Кусочные аппроксимации 146
4. Проекционные методы 4. 5. Кусочные аппроксимации 146
 4. Проекционные методы 4. 5. Кусочные аппроксимации 147
4. Проекционные методы 4. 5. Кусочные аппроксимации 147
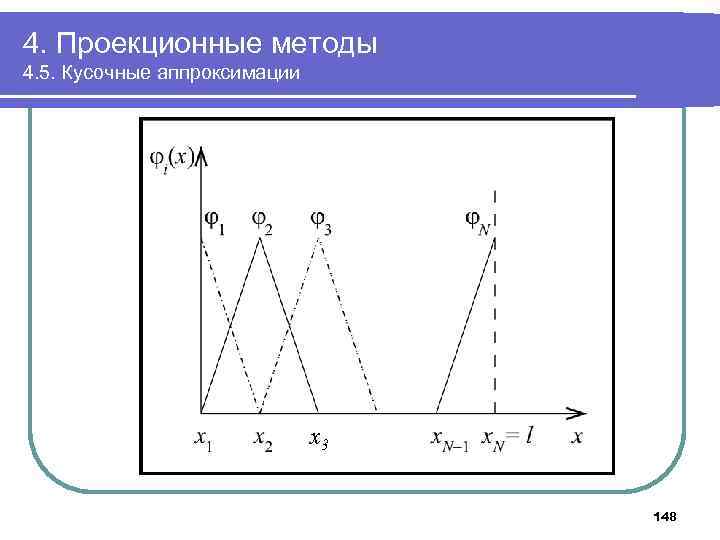 4. Проекционные методы 4. 5. Кусочные аппроксимации x 3 148
4. Проекционные методы 4. 5. Кусочные аппроксимации x 3 148
 4. Проекционные методы 4. 5. Кусочные аппроксимации В методе коллокаций 149
4. Проекционные методы 4. 5. Кусочные аппроксимации В методе коллокаций 149
 4. Проекционные методы 4. 5. Кусочные аппроксимации 150
4. Проекционные методы 4. 5. Кусочные аппроксимации 150
 4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 151
4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 151
 4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 152
4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 152
 4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 153
4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 153
 4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 154
4. Проекционные методы 4. 6. Вариационный подход к приближенному решению ДУ 154


