МЕТОДЫ СОРТИРОВКИ Сортировка упорядочение элементов множества в

МЕТОДЫ СОРТИРОВКИ Сортировка – упорядочение элементов множества в порядке возрастания или убывания некоторого ключа. Внутренняя С – сортировка элементов в оперативной памяти Внешняя С – сортировка элементов на носителях (файлы и т. д. ) Устойчивая С – не меняет относительный порядок элементов, имеющих одинаковые ключи

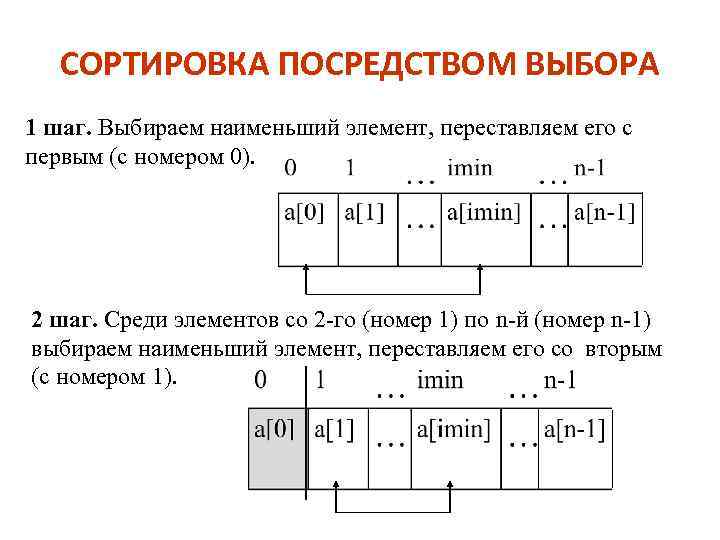СОРТИРОВКА ПОСРЕДСТВОМ ВЫБОРА 1 шаг. Выбираем наименьший элемент, переставляем его с первым (с номером 0). 2 шаг. Среди элементов со 2 -го (номер 1) по n-й (номер n-1) выбираем наименьший элемент, переставляем его со вторым (с номером 1).

СОРТИРОВКА ПОСРЕДСТВОМ ВЫБОРА k-й шаг. Среди элементов со k-го (номер k-1) по n-й (номер n-1) выбираем наименьший элемент, переставляем его с k-м (с номером k-1). (n-1)-й шаг. Среди элементов со (n-1)-го (номер n-2) по n-й (номер n-1) выбираем наименьший элемент, переставляем его с (n-1)-м (с номером n-2).

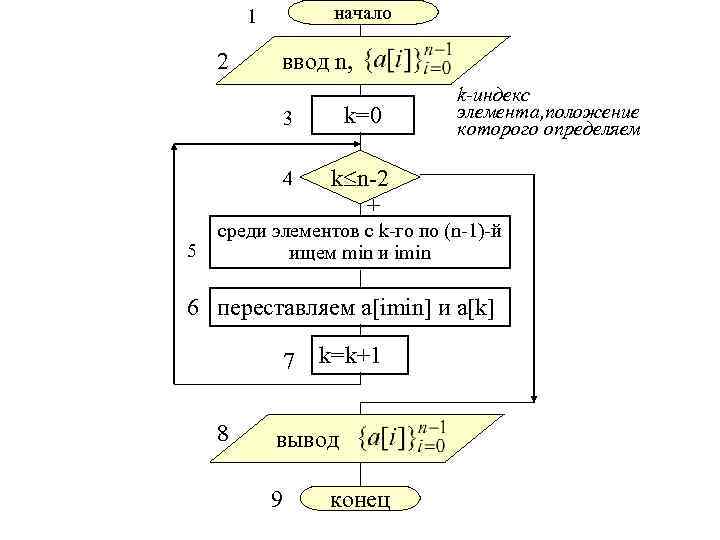начало 1 2 ввод n, 3 4 5 k=0 k-индекс элемента, положение которого определяем k n-2 + среди элементов с k-го по (n-1)-й ищем min и imin 6 переставляем a[imin] и a[k] 7 8 k=k+1 вывод 9 конец

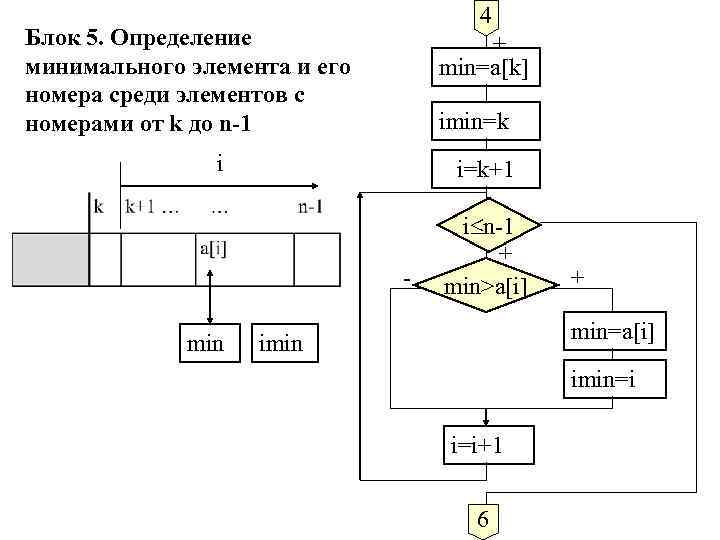4 Блок 5. Определение минимального элемента и его номера среди элементов с номерами от k до n-1 + min=a[k] imin=k i i=k+1 min i n-1 + min>a[i] + min=a[i] imin=i i=i+1 6

Блок 6. Перестановка элементов с номерами k и imin 5 5 -1 a[imin]=a[k] 5 -2 a[k]=min imin. . . 7 5 -1 5 -2 min imin

void main() //сортировка посредством выбора {int n, imin, k, i; float a[20], min; <ввод n, {a[i], i=0, …, n-1}> for (k=0; k<=n-2; k=k+1) {min=a[k]; imin=k; for (i=k+1; i<=n-1; i=i+1) if (min>a[i]) {min=a[i]; imin=i; } a[imin]=a[k]; a[k]=min; } <вывод {a[i], i=0, …, n-1}> }

ЧИСЛО СРАВНЕНИЙ ПРИ СОРТИРОВКЕ ПОСРЕДСТВОМ ВЫБОРА Итого: 1+2+…+(n-2)+(n-1) =

ОБМЕННАЯ СОРТИРОВКА Просмотр массива и сравнение соседних элементов. a[i]>a[i+1] - инверсия, элементы необходимо поменять местами. За один просмотр хотя бы один элемент занимает нужное место: максимальный элемент поднимается «наверх» «метод пузырька» Процесс повторяется, пока есть инверсии. Признак наличия инверсий (флажок): max

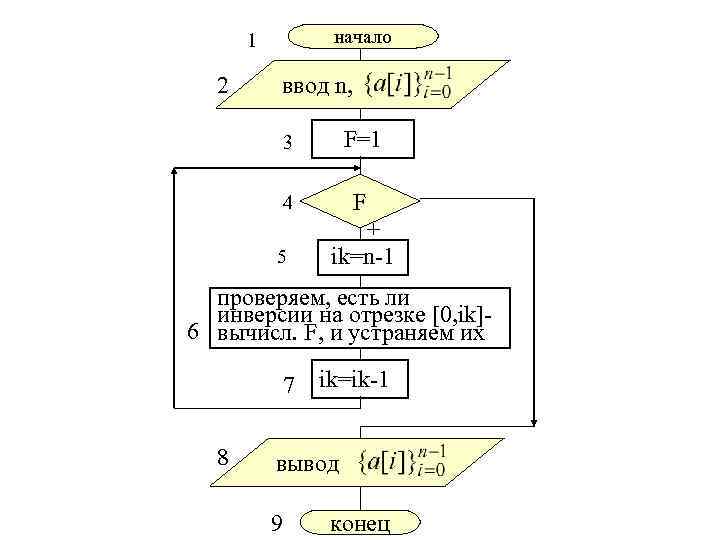начало 1 2 ввод n, 3 F=1 4 F 5 + ik=n-1 проверяем, есть ли инверсии на отрезке [0, ik]6 вычисл. F, и устраняем их 7 8 ik=ik-1 вывод 9 конец

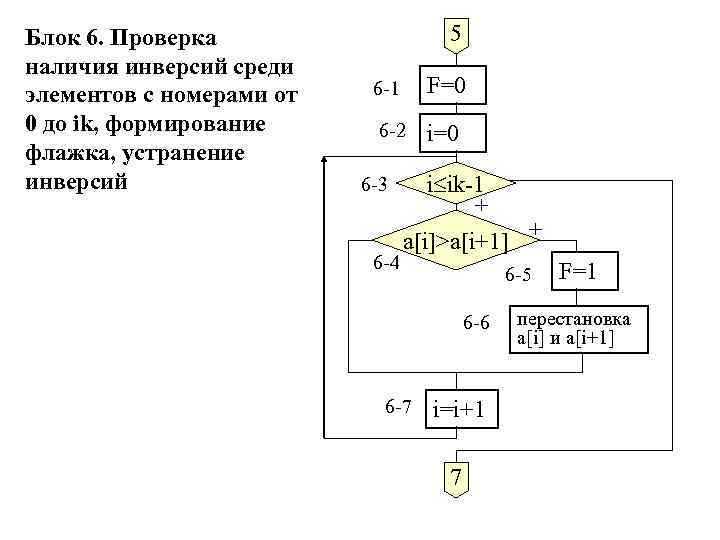Блок 6. Проверка наличия инверсий среди элементов с номерами от 0 до ik, формирование флажка, устранение инверсий 5 6 -1 F=0 6 -2 i=0 6 -3 6 -4 i ik-1 + a[i]>a[i+1] + 6 -5 6 -6 6 -7 i=i+1 7 F=1 перестановка a[i] и a[i+1]

Блок 6 -6. Перестановка соседних элементов 2 a[i] a[i+1] 3 1 b 6 -5 1 b=a[i] 2 a[i]=a[i+1] 3 a[i+1]=b 6 -7 b - буферная переменная

void main() //метод пузырька {int n, F, ik, i; float a[20], b; <ввод n, {a[i], i=0, …, n-1}> F=1; while(F) {ik=n-1; F=0; for (i=0; i<=ik-1; i=i+1) if (a[i]>a[i+1]) {F=1; b=a[i]; a[i]=a[i+1]; a[i+1]=b; } ik=ik-1; //один элемент встал на место } <вывод {a[i], i=0, …, n-1}> }

Число сравнений при обменной сортировке Если нет инверсий - один просмотр. Если массив упорядочен «наоборот» (по убыванию) - максимальное число просмотров (n-1). Обменную сортировку выгодно применять, если в исходном массиве мало инверсий Итого: 1+2+…+(n-2)+(n-1) = МАКСИМАЛЬНОЕ ЧИСЛО СРАВНЕНИЙ

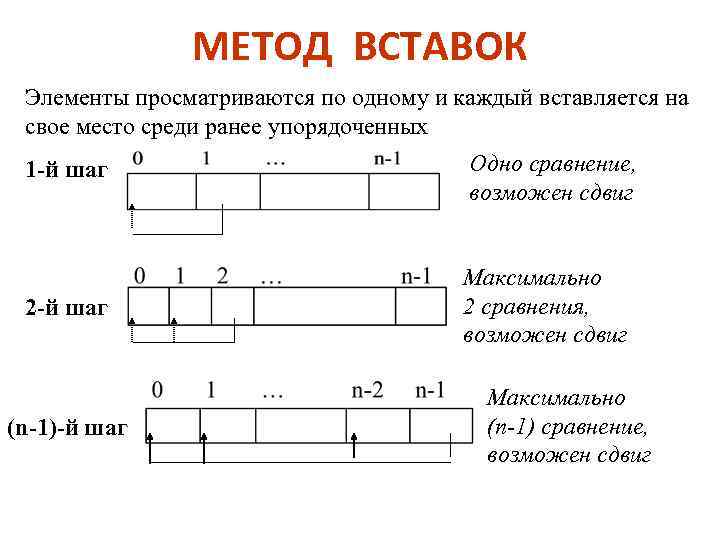МЕТОД ВСТАВОК Элементы просматриваются по одному и каждый вставляется на свое место среди ранее упорядоченных 1 -й шаг Одно сравнение, возможен сдвиг 2 -й шаг Максимально 2 сравнения, возможен сдвиг (n-1)-й шаг Максимально (n-1) сравнение, возможен сдвиг

МЕТОД ВСТАВОК МАКСИМАЛЬНОЕ ЧИСЛО СРАВНЕНИЙ 1+2+…+(n-2)+(n-1) = Основной недостаток: необходимость многократного сдвига элементов

МЕТОД ВСТАВОК unsigned int i, j, temp; for(i=1; i=0) { a[j+1] = a[j]; j = j-1; } a[j+1] = temp; }

СОРТИРОВКА С ПОМОЩЬЮ ПОДСЧЕТА Предполагается, что в исходном массиве нет равных элементов. Каждый элемент сравнивается с остальными. Для каждого элемента подсчитывается число элементов, меньших его (т. н. ключ). Значение ключа определяет место элемента в упорядоченном массиве. массив a массив k (ключи) в начале k заполнен нулями

СОРТИРОВКА С ПОМОЩЬЮ ПОДСЧЕТА На каждом сравнении (i

СОРТИРОВКА С ПОМОЩЬЮ ПОДСЧЕТА 1 -й проход a[0] сравнивается с a[1], a[2], …a[n-1] - (n-1) сравнений 2 -й проход a[1] сравнивается с a[2], a[3], …a[n-1] - (n-2) сравнений … (n-1)-й проход a[n-2] сравнивается с a[n-1] - 1 сравнение Всего сравнений: 1+2+…+(n-2)+(n-1) =

СОРТИРОВКА С ПОМОЩЬЮ ПОДСЧЕТА После всех проходов элементы переписываются в другой массив, причем индекс a[i] в новом массиве равен k[i]. Основной недостаток метода: необходимость переписывания элементов в другой массив.

ВЫВОД: ВСЕ ПРОСТЕЙШИЕ МЕТОДЫ СОРТИРОВКИ ЭКВИВАЛЕНТНЫ ПО КОЛИЧЕСТВУ СРАВНЕНИЙ ИМЕЮТ ПРАКТИЧЕСКИ ОДИНАКОВОЕ БЫСТРОДЕЙСТВИЕ КОЛИЧЕСТВО СРАВНЕНИЙ ДЛЯ ПРОСТЕЙШИХ МЕТОДОВ СОРТИРОВКИ ПРОПОРЦИОНАЛЬНО n 2/2 СУЩЕСТВУЮТ БОЛЕЕ БЫСТРОДЕЙСТВУЮЩИЕ И БОЛЕЕ СЛОЖНЫЕ МЕТОДЫ, ДЛЯ КОТОРЫХ ЧИСЛО СРАВНЕНИЙ ПРОПОРЦИОНАЛЬНО nlog 2 n В основе быстродействующих методов - алгоритм слияния двух упорядоченных массивов

ЗАДАЧА СЛИЯНИЯ ДВУХ УПОРЯДОЧЕННЫХ МАССИВОВ Имеется два упорядоченных массива: a[0] a[1] … a[m-1] b[0] b[1] … b[n-1], вообще говоря, n m. Требуется из элементов этих массивов получить упорядоченный массив c[0] c[1] . . . c[n+m-1].

ЗАДАЧА СЛИЯНИЯ ДВУХ УПОРЯДОЧЕННЫХ МАССИВОВ Два подхода 1. a[0], a[1], …, a[m-1], b[0], b[1], …, b[n-1], затем упорядочение порядка (n+m-1)2 сравнений. 2. Слияние: запись в массив с элементов a и b таким образом, чтобы сразу получился упорядоченный массив. пока не закончится один из b исходных массивов a цикл если a[i]

начало ввод k=0; i=0; j=0; i m-1&&j n-1 + a[i]

1 2 i m-1 + c[k]=a[i] j n-1 + c[k]=b[j] k=k+1 i=i+1 j=j+1 2 вывод Заполнение массива с оставшимися элементами одного из исходных массивов

void main() { int n, m, i, j, k; float a[20], b[20], c[40]; <ввод m, {a[i], i=0, …, m-1}> <ввод n, {b[j], j=0, …, n-1}> k=0; i=0; j=0; while (i<=m-1&&j<=n-1) if(a[i] }

БЫСТРАЯ СОРТИРОВКА ИДЕЯ: 1. Разбиение массива на подмассивы 2. Упорядочение подмассивов 3. Слияние подмассивов

1 уровень a[0] a[1] a[2] a[3] a[4] a[5] … a[n-3] a[n-2] a[n-1] Число отрезков =n/2 Длина отрезка=2 Число сравнений 1* n/2 2 уровень a[0] a[1] a[2] a[3] a[4] a[5] … a[n-4] a[n-3] a[n-2] a[n-1] Число отрезков =n/4 Длина отрезка=4 Число сравнений 3* n/4 3 уровень Последний k-й уровень Число отрезков =n/8 Длина отрезка=8 Число сравнений 7* n/4 Число отрезков =1 Длина отрезка=n Число сравнений n-1 (слияние n/2+n/2) 2 k=n k=log 2 n - число уровней, на каждом уровне n сравнений Число сравнений n log 2 n

МЕТОД ХОАРА Идея: выбор опорного элемента и разбиение относительно него массива на две части опорный элемент a[0] a[1]. . . a[k-1] a[k+1]… a[n-1] меньше a[k] больше a[k] Число сравнений n log 2 n Важно: выбор опорного элемента!