МЕТОДЫ СИСТЕМНОГО АНАЛИЗА В ЭКОНОМИКЕ И УПРАВЛЕНИИ

МЕТОДЫ СИСТЕМНОГО АНАЛИЗА В ЭКОНОМИКЕ И УПРАВЛЕНИИ

Пример решения задачи методами математического программирования В качестве примера применения методов математического программирования для решения задач управления в экономике рассмотрим решение следующей задачи. На предприятии работает три цеха, в которых выпускается два вида продукции. Известны следующие показатели работы цехов: загрузка каждого цеха в процентах по каждому виду продукции (aij); прибыль от реализации продукции в рублях (cj). Требуется определить, сколько изделий каждого вида необходимо производить при возможно полной загрузке цехов, чтобы получить максимальную прибыль за период. Условия задачи можно представить в виде табл. Форма записи условий в задаче математического программирования Математически задача формулируется в виде целевой функции, определяющей максимизацию прибыли Продукция Цех (участок) Цена изделия Ц 1 Ц 2 Ц 3 П 1 5 % 1, 6 % 2, 9 % 240 руб. П 2 4 % 6, 4 % 5, 8 % 320 руб. Максимальная загрузка цеха 100 %

Математически задача формулируется в виде целевой функции, определяющей максимизацию прибыли Ограничения по цехам, связанные с их 100% загрузкой, записываются в виде неравенств: Так как в нашем примере все ограничения однородны, то их можно записать в виде В задаче можно ввести несколько групп ограничений, например по имеющимся материалам, зарплате рабочих и пр. Решение задачи графически представлено на рис. 5. 3. Ограничения задают область допустимых решений, а наклон прямой определяет точку последнего ее пересечения с областью допустимых решений, которая и является наилучшим решением (оптимумом). В нашей задаче это . В случае большого числа ограничений графическая интерпретация задачи затруднена, поэтому используются специальные (симплекс метод) пакеты прикладных программ для их поиска, однако суть решения при этом не меняется.

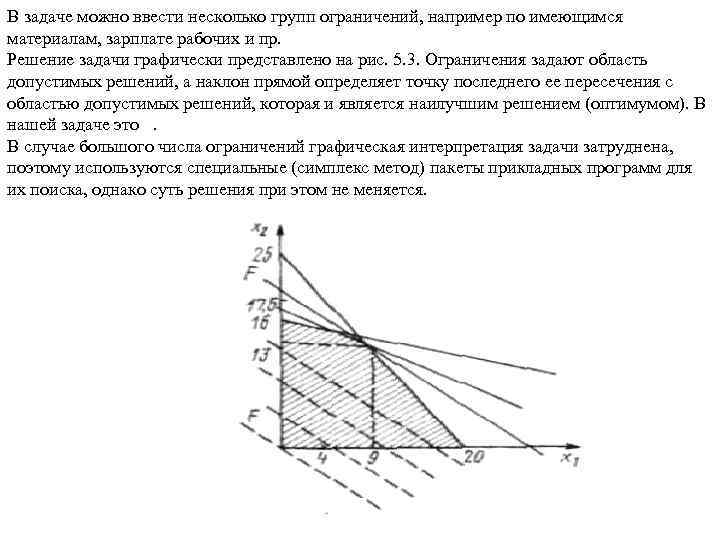В задаче можно ввести несколько групп ограничений, например по имеющимся материалам, зарплате рабочих и пр. Решение задачи графически представлено на рис. 5. 3. Ограничения задают область допустимых решений, а наклон прямой определяет точку последнего ее пересечения с областью допустимых решений, которая и является наилучшим решением (оптимумом). В нашей задаче это . В случае большого числа ограничений графическая интерпретация задачи затруднена, поэтому используются специальные (симплекс метод) пакеты прикладных программ для их поиска, однако суть решения при этом не меняется.

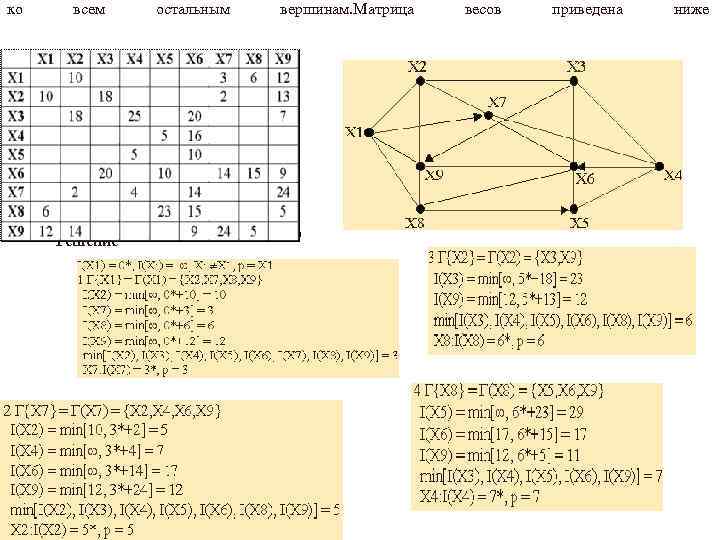ко всем остальным вершинам. Матрица весов приведена Решение рис. 2. 31 ниже

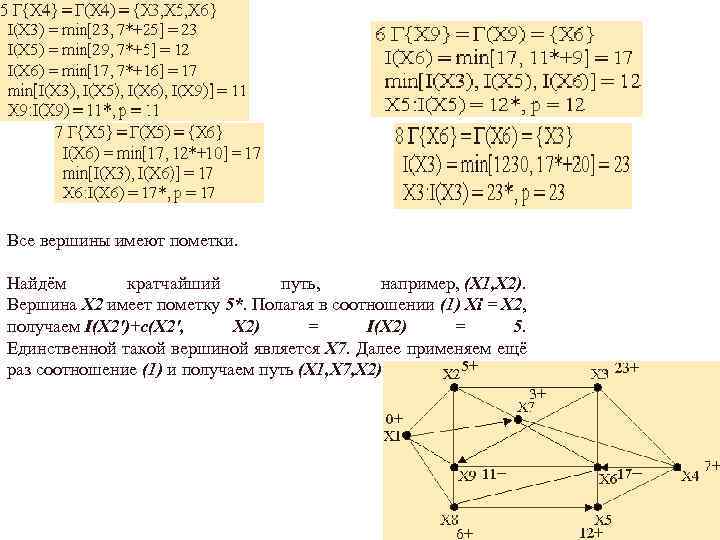Все вершины имеют пометки. Найдём кратчайший путь, например, (Х 1, Х 2). Вершина Х 2 имеет пометку 5*. Полагая в соотношении (1) Хi = Х 2, получаем I(X 2')+с(Х 2', Х 2) = I(X 2) = 5. Единственной такой вершиной является Х 7. Далее применяем ещё раз соотношение (1) и получаем путь (Х 1, Х 7, Х 2)

Матричный метод. Если матрица А системы линейных уравнений невырожденная, т. е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A-1 B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A -1 B называют матричным способом решения системы, или решением по методу обратной матрицы. Пример. Решить матричным способом систему уравнений x 1 - x 2 + x 3 = 6, 2 x 1 + x 2 + x 3 = 3, x 1 + x 2 +2 x 3 = 5. Решение. Обозначим Тогда данная система уравнений запишется матричным уравнением AX=B. Поскольку то матрица A невырождена и поэтому имеет обратную:

Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A-1 B. В данном случае и, следовательно, Выполняя действия над матрицами, получим: x 1 = 1/5(1× 6+3× 3 -2× 5) = 1/5 (6+9 -10) = 1, x 2 = 1/5 (-3× 6 +1× 3 - 1× 5) = 1/5 (- 18 + 3 + 5) = -2, x 3 = 1/5 (1× 6 - 2× 3 + 3× 5) = 1/5 (6 -6 + 15) = 3. Итак, X = (1, -2, 3)T.

Статистические модели Показатели Наличие товаров в розничных торговых предприятиях Сумма, тыс. руб. 590 Наличие товаров на распределенных складах 260 Товары в пути Тара ящичная свободная и под товаром 15 2 Наличие товаров на ответственном хранении у поставщика, закупленные и оплаченные данной торговой организацией 6 Товары сезонного накопления 14 Товары, принятые от населения и 5 кооперативов на комиссию Дополнительные сведения: план оборота на месяц Норматив товарных запасов в днях 960

Статистические модели Определите: Общую сумму товарных запасов, отражаемую в статистической отчетности; товарные запасы текущего хранения; товарные запасы в днях; отклонения товарных запасов от норматива в днях и в сумме. Сделайте выводы. Решение Согласно инструкции Госкомстата России по определению розничного товарооборота и товарных запасов общая сумма товарных запасов, отражаемая в статистической отчетности равна 590+260+15+2+6+14+5 = 892 тыс. руб. Товарные запасы текущего хранения: 892 -14+15 = 893 тыс. руб. Товарные запасы в днях вычисляются отношением суммы запасов текущего хранения на отчетную дату к однодневному плановому обороту. Однодневный товарооборот определяется делением оборота на число дней в периоде: 960/30 = 32 тыс. руб. Товарные запасы в днях: 893/32 = 27, 9 дн. То есть товарных запасов хватит на 27, 9 дней. 4. Отклонения товарных запасов от норматива в днях: 27, 9 -21 = 6, 9 дн.

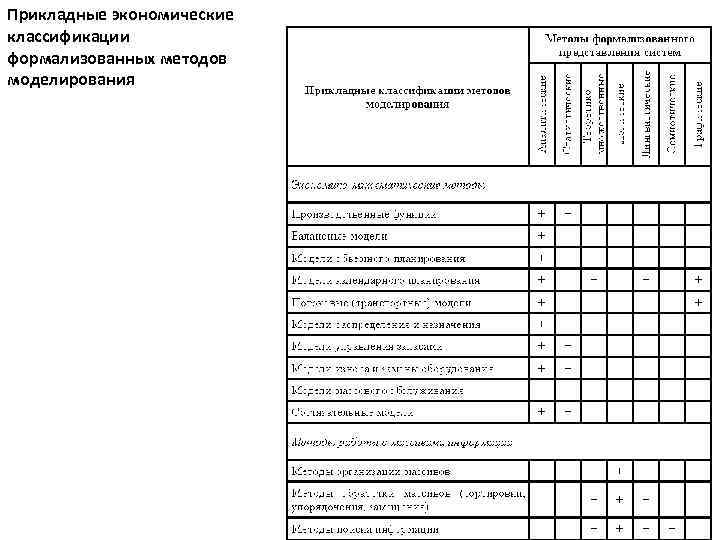Прикладные экономические классификации формализованных методов моделирования

Классификации, ориентированные на прикладные направления, должны пересекаться с классификациями, базирующимися на математических представлениях. Поэтому вырабатываемая для целей системного анализа классификация должна быть не одномерной. Так, например, приведенная в табл. 5. 3. классификация отражает взаимное соответствие классификации методов формализованного преставления систем (см. табл. 5. 1. ) – горизонтальная шкала и прикладных классификаций – вертикальная шкала. В таблице отражено, на каких методах формализованного представления систем может базироваться разработка моделей, выделяемых в прикладных классификациях.