Методы синтеза ЦФ СИНТЕЗ ФИЛЬТРОВ КИХ

Методы синтеза ЦФ

СИНТЕЗ ФИЛЬТРОВ КИХ

Синтез фильтров КИХ • При наличии импульсной характеристики ее достаточно оцифровать с нужной частотой дискретизации. • При наличии АЧХ используется два метода: метод окон (метод разложения в ряд Фурье) и оптимизационный.

Метод окон Этот метод имеет две реализации: • Аналитическая • Дискретная

Метод окон • Аналитический метод предполагает наличие частотной характеристики в виде формулы H(f): – Эта формула приводится к дискретной частотной характеристике H(m) – Полученное выражение H(m) подставляется в формулу ОДПФ – Полученная функция h(k) является импульсной характеристикой, а ее отсчеты – искомыми коэффициентами фильтра.

Метод окон • При отсутствии ЧХ, заданной аналитически, применяют второй способ: – Заданная ЧХ дискретизируется в частотной области в интервале [–fд /2; fд /2] – Полученные отсчеты подставляются в формулу ОДПФ – Полученная функция h(k) является импульсной характеристикой, а ее отсчеты – искомыми коэффициентами фильтра.

Метод окон: иллюстрации 1. Идеальная непрерывная ЧХ: H(f) 2. Ее дискретное представление: H(m)

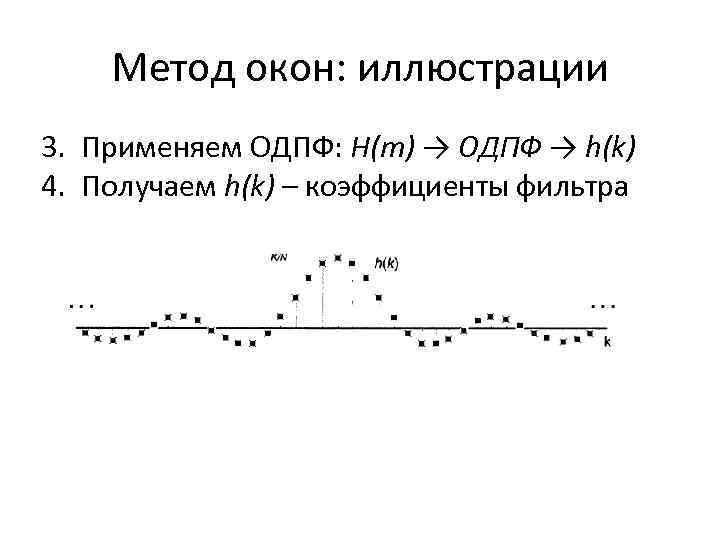Метод окон: иллюстрации 3. Применяем ОДПФ: H(m) → ОДПФ → h(k) 4. Получаем h(k) – коэффициенты фильтра

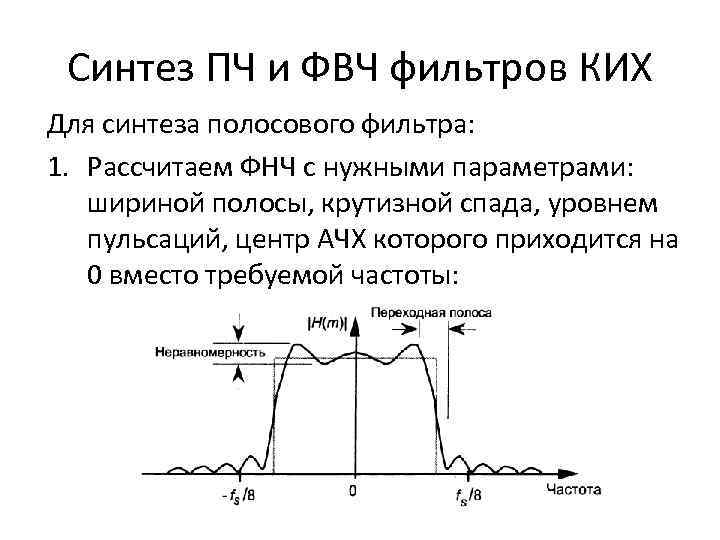Синтез ПЧ и ФВЧ фильтров КИХ Для синтеза полосового фильтра: 1. Рассчитаем ФНЧ с нужными параметрами: шириной полосы, крутизной спада, уровнем пульсаций, центр АЧХ которого приходится на 0 вместо требуемой частоты:

Синтез ПЧ и ФВЧ фильтров КИХ 2. Сместим полученную H(m) на нужную частоту, воспользовавшись свойством сдвига ДПФ: Пусть последовательность y получена путем сдвига последовательности x на n отсчетов: y(t) = x (t - n), тогда ДПФ(y) = ДПФ(x) exp(-j 2 nk/N) …перерассчитаем h(k) полосового фильтра: h. П(k) = h. НЧ(k) exp(-j 2 nk/N)

Синтез ПЧ и ФВЧ фильтров КИХ То есть, нужно умножить коэффициенты ФНЧ на дискретную синусоиду, частота которой равна нужной центральной частоте. В случае же ФВЧ эта частота равна половине частоты дискретизации. Тогда коэффициенты ФНЧ умножаются на последовательность (1, -1, 1, -1…).

СИНТЕЗ ФИЛЬТРОВ БИХ

Синтез фильтров БИХ Применяются следующие разновидности расчета фильтров: • Синтез по аналоговому прототипу 1. Метод инвариантной импульсной характеристики 2. Метод билинейного преобразования 3. Метод дискретизации дифференциального уравнения аналоговой цепи • Прямой метод синтеза • Эвристические методы (Алгоритм Герцеля)

Метод инвариантного преобразования импульсной характеристики Импульсная характеристика ЦФ получается путем дискретизации ИХ фильтра-прототипа. Значения импульсной характеристики ЦФ h(k ) должны быть равны значениям ИХ фильтра-прототипа в отсчетные моменты времени t=k.

Метод инвариантного преобразования импульсной характеристики Затем, применяя к ИХ ЦФ Z-преобразование, можно найти системную функцию и составить алгоритм ЦФ. Степень приближения ЧХ ЦФ к ЧХ прототипа зависит от выбора шага дискретизации. При необходимости можно вычислить ЧХ ЦФ, введя в системной функции замену Z=exp(j ), и сравнить ее с ЧХ прототипа.

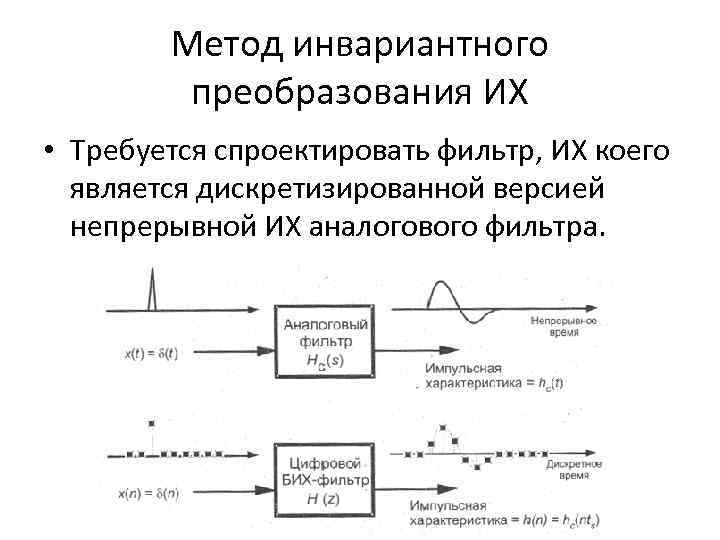Метод инвариантного преобразования ИХ • Требуется спроектировать фильтр, ИХ коего является дискретизированной версией непрерывной ИХ аналогового фильтра.

Метод инвариантного преобразования ИХ • Соответствие этих характеристик предполагает, что мы можем отобразить каждый полюс передаточной функции аналогового фильтра H(p) в р-плоскости на полюс передаточной функции дискретного фильтра в z-плоскости.

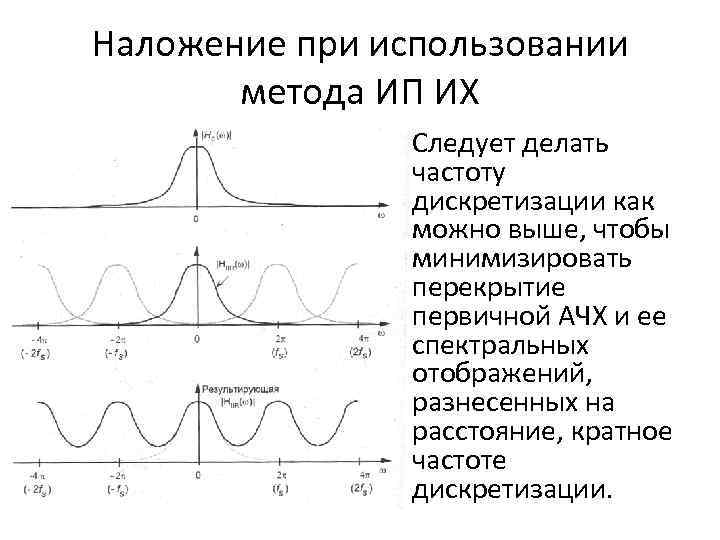Наложение при использовании метода ИП ИХ Следует делать частоту дискретизации как можно выше, чтобы минимизировать перекрытие первичной АЧХ и ее спектральных отображений, разнесенных на расстояние, кратное частоте дискретизации.

Метод инвариантного преобразования ИХ • Методы проектирования БИХ-фильтров на основе инвариантного преобразования импульсной характеристики больше всего подходят для проектирования узкополосных фильтров. • То есть, для ФНЧ, частоты среза коих намного меньше частоты дискретизации.

Метод инвариантного преобразования ИХ Первая методика: 1. Получить аналоговый фильтр с требуемой АЧХ, что означает наличие передаточной функции H(p). 2. По передаточной функции H(p) с помощью преобразования Лапласа определить непрерывную импульсную характеристику h(t).

Метод инвариантного преобразования ИХ 3. Определить частоту дискретизации, исходя из требований к сигналу и оборудованию. Частота дискретизации должна быть как можно выше. 4. Найти z-преобразование ИХ h(t) и получить передаточную функцию БИХ-фильтра H(z).

Метод инвариантного преобразования ИХ 5. Подставить значение интервала дискретизации в H(z). Этим обеспечивается равенство отсчетов дискретной ИХ значениям непрерывной ИХ в моменты времени t=kτ. 6. Записать разностное уравнение и тем самым получить коэффициенты фильтра.

Метод инвариантного преобразования ИХ Вторая методика: 1. Исходный фильтр математически разбивается на M фильтров с одним полюсом. 2. Каждый из этих фильтров аппроксимируется однополюсным цифровым. 3. Набор M однополюсных фильтров аналитически объединяется в БИХ-фильтр M-го порядка.

Оптимизационный метод проектирования БИХ-фильтров • В случае, если требуемая АЧХ сложна и не выражается формулой, применяется оптимизационный метод. • Суть его состоит в итерационном подборе коэффициентов фильтра и сравнении результирующей АЧХ с заданной. • Количество итераций ограничено либо напрямую, либо заданной величиной ошибки.

Прямой метод синтеза БИХ фильтров • Прямой синтез ЦФ сводится к нахождению функции, аппроксимирующей заданную ЧХ так, чтобы в результате получилось дробно -рациональное выражение для системной функции ЦФ. • Для того, чтобы H(Z) была дробнорациональной, необходимо, чтобы аппроксимирующая ЧХ была дробнорациональной относительно exp(j ).

Подводные камни проектировании БИХ-фильтров • Квантование коэффициентов (ограниченная точность) приводит к смещению нулей и полюсов и искажению АЧХ. • Переполнение на промежуточных этапах: результат сложения и умножения может сильно превышать величину входных и выходных сигналов.

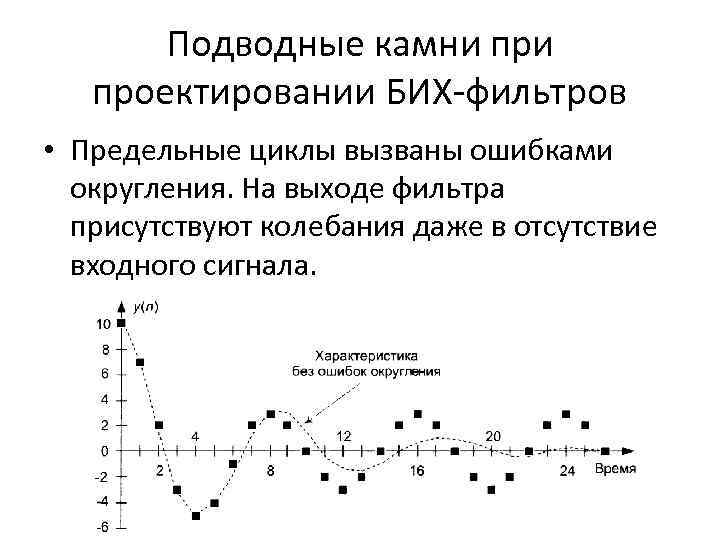Подводные камни проектировании БИХ-фильтров • Предельные циклы вызваны ошибками округления. На выходе фильтра присутствуют колебания даже в отсутствие входного сигнала.