Методы расчета электрических цепей Основные: 1. Непосредственное применение

Методы расчета электрических цепей Основные: 1. Непосредственное применение законов Кирхгофа 2. Метод контурных токов 3. Метод узловых потенциалов 4. Метод эквивалентного генератора 5. Метод наложения n-число узлов в электрической цепи m- число ветвей в электрической цепи K – число источников тока

Расчет цепи по законам Кирхгофа Исходные данные 1 R 1 = R 2 =100 Ом Е 3 =100 В Ik 1=1 A, Ik 2=2 A I 1 Н. о. I 3 2 Узлов – (n= 3) , ветвей- (m= 5), источников тока( k=2) Число уравнений по 1 З. К – (n-1)=3 -1=2 I 2 Число уравнений по 2 З. К – (m-n+1 -k) 3 (m-n+1 -k)=5 - 3+1 - 2 = 1 I 1 - Ik 2 + I 3=0 для узла 1 По первому закону Ik 2 - Ik 1 – I 2=0 для узла 2 Кирхгофа

I 1 R 1 = - E 3 по второму З. К. для большого контура. I 1 - Ik 2 + I 3=0 Ik 2 - Ik 1 – I 2=0 система I 1 R 1 = - E 3 Решение

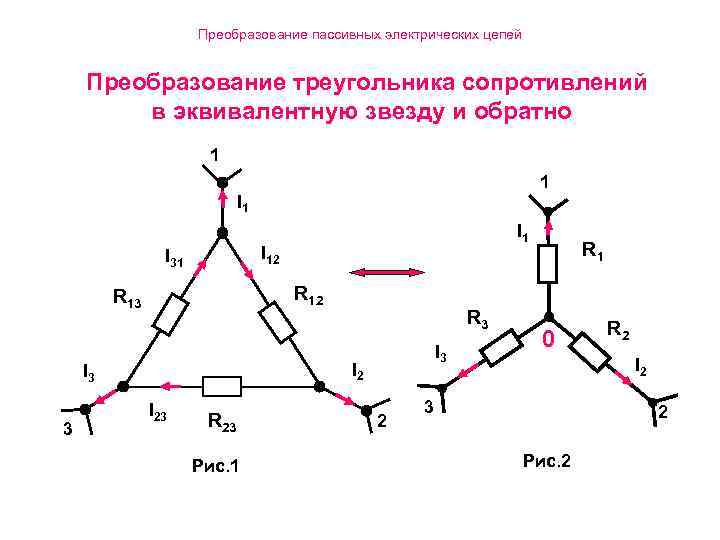Преобразование пассивных электрических цепей Преобразование треугольника сопротивлений в эквивалентную звезду и обратно 1 I 1 I 31 I 12 R 13 R 12 R 3 R 2 I 3 0 I 3 I 23 2 3 R 23 2 Рис. 1 Рис. 2

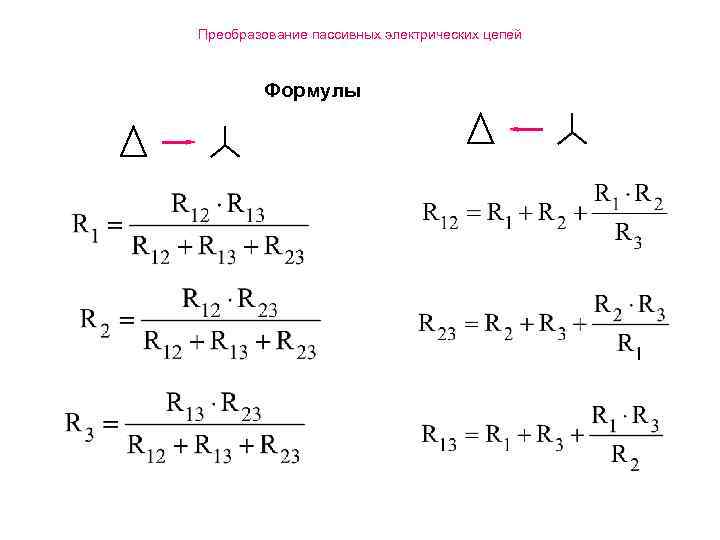Преобразование пассивных электрических цепей Формулы

Метод контурных токов Система уравнений для произвольной цепи I 11 R 11+I 22 R 12+I 33 R 13+ +Imm. R 1 m=E 11 I 11 R 21+I 22 R 22+I 33 R 23+ +Imm. R 2 m=E 22 I 11 R 31+I 22 R 32+I 33 R 33+ +Imm. R 3 m=E 33 I 11 Rm 1+I 22 Rm 2+I 33 Rm 3+ +Imm. Rmm=Emm Алгебраическое дополнение Электрические цепи постоянного тока

Порядок расчета задач методом контурных токов 1. Произвольно выбираются условно –положительные направления истинных токов в ветвях. 2. Выбираются (m+n-1 -k) взаимно – независимых контуров, в которых произвольно задаются направлениями контурных токов. 3. Для выбранных контуров составляется система контурных уравнений. ( 1). 4. Полученная система решается любым известным методом относительно неизвестных контурных токов. 5. Истинные токи в ветвях определяются как алгебраическая сумма контурных токов. 6. Производится проверка полученного решения с помощью уравнения баланса мощности , либо по второму закону Кирхгофа.

Некоторые замечания: • Решение по методу контурных токов невозможно проверить по первому закону Кирхгофа; • Наличие источников тока не увеличивает количества независимых контуров (неизвестных контурных токов); • Метод контурных токов рациональнее использовать, если число независимых контуров меньше числа узлов (т. е. (m-n+1)

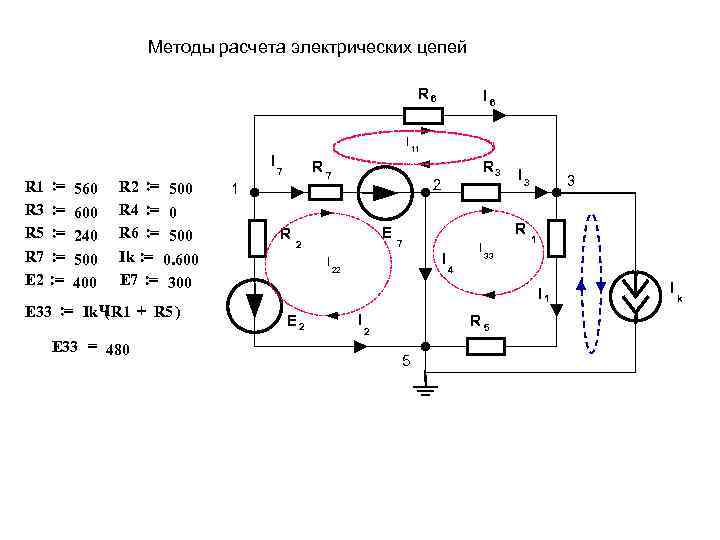Методы расчета электрических цепей R 6 I 6 I 11 I R 7 R 3 7 I 3 3 R 1 : = 560 R 2 : = 500 1 2 R 3 : = 600 R 4 : = 0 R 5 : = 240 R 6 : = 500 R E R 7 1 2 I R 7 : = 500 Ik : = 0. 600 I 33 22 4 E 2 : = 400 E 7 : = 300 I 1 I k E 33 : = Ik ЧR 1 + R 5 ) ( E 2 I R 5 2 E 33 = 480 5

Уравнения 1. 1. E 33 = = 480

й(R 7+ R 6+ R 3) -R 7 -R 3 щ к ъ D : = к -R 7 (R 2+ R 7) 0 ъ к ъ л -R 3 0 (R 3+ R 1+ R 5 ) ы 9 D = 1. 53 ґ 10 й ( - E 7 ) - R 7 - R 3 щ к ъ D 11 : = к( - E 2 + E 7 ) ( R 2 + R 7 ) 0 ъ к ъ л E 33 0 ( R 3 + R 1 + R 5)ы D 11 = - 2. 02 ґ 10 8

й( R 7 + R 6 + R 3) -E 7 -R 3 щ к ъ D 22 : = к -R 7 ( -E 2 + E 7) 0 ъ к л -R 3 E 33 ( R 3 + R 1 + R 5) ъ ы D 22 = - 2. 54 ґ 10 8 й( R 7 + R 6 + R 3) к - R 7 - E 7 щ ъ D 33 : = к - R 7 ( R 2 + R 7) ( - E 2 + E 7 ) ъ к ъ л - R 3 0 E 33 ы D 33 = 4. 38 ґ 10 8 D 11 D 22 D 33 I 11 : = I 22 : = I 33 : = D D

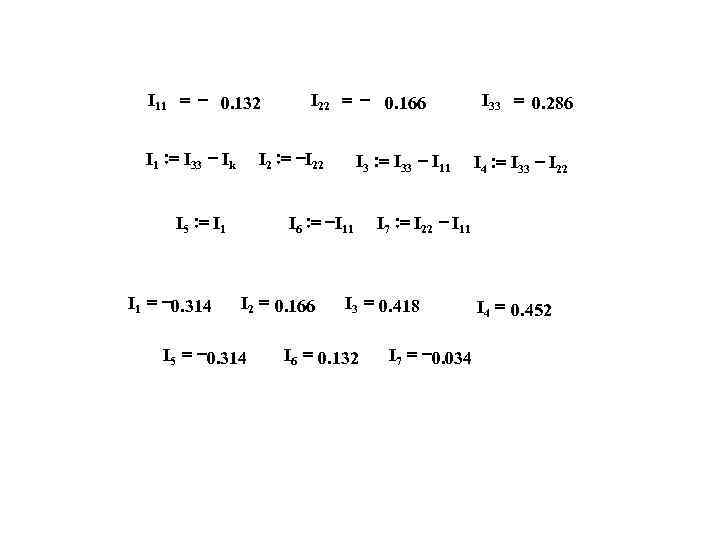I 11 = - 0. 132 I 22 = - 0. 166 I 33 = 0. 286 I 1 : = I 33 - Ik I 2 : = -I 22 I 3 : = I 33 - I 11 I 4 : = I 33 - I 22 I 5 : = I 1 I 6 : = -I 11 I 7 : = I 22 - I 11 I 1 = -0. 314 I 2 = 0. 166 I 3 = 0. 418 I 4 = 0. 452 I 5 = -0. 314 I 6 = 0. 132 I 7 = -0. 034

Метод узловых потенциалов Порядок расчета электрической цепи методом узловых потенциалов 1. Выбираем условно-положительные направления токов в цепи. 2. Выбираем узел, потенциал которого принимается равным нулю. 3. Записываем для остальных узлов уравнения по методу узловых потенциалов. 4. Решаем систему уравнений и определяем потенциалы узлов. 5. По закону Ома для участка цепи определяем токи в ветвях электрической цепи. 6. Осуществляем проверку полученного решения по законам Кирхгофа или по уравнению баланса мощности. Электрические цепи постоянного тока

Замечания к методу узловых потенциалов 1. Обязательно заземляется узел к которому присоединяется ветвь, не имеющая сопротивлений. В противном случае проводимость ветви становится равной бесконечности и задача не имеет решения по МУП. 2. Проводимость ветви с последовательно соединенными сопротивлениями определяется как величина обратная полному сопротивлению ветви. 3. Если заземлить узел к которому присоединена ветвь , имеющая ЭДС, но не имеющая сопротивлений, то потенциал второго узла будет равен . Е 1 2

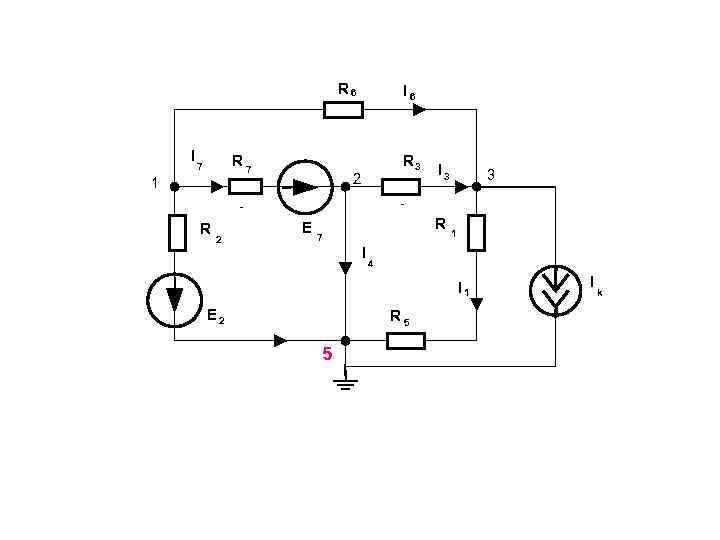R 6 I R 7 R 3 7 I 3 3 1 2 R E R 7 1 2 I 4 I 1 I k E 2 R 5 5

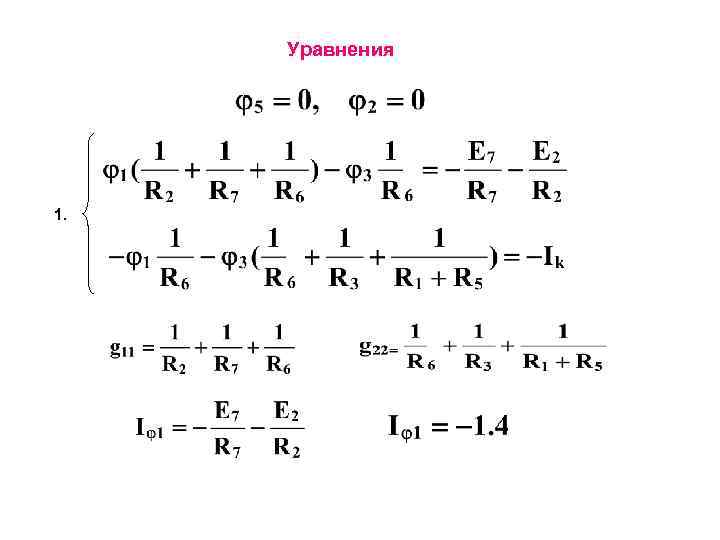Уравнения 1.

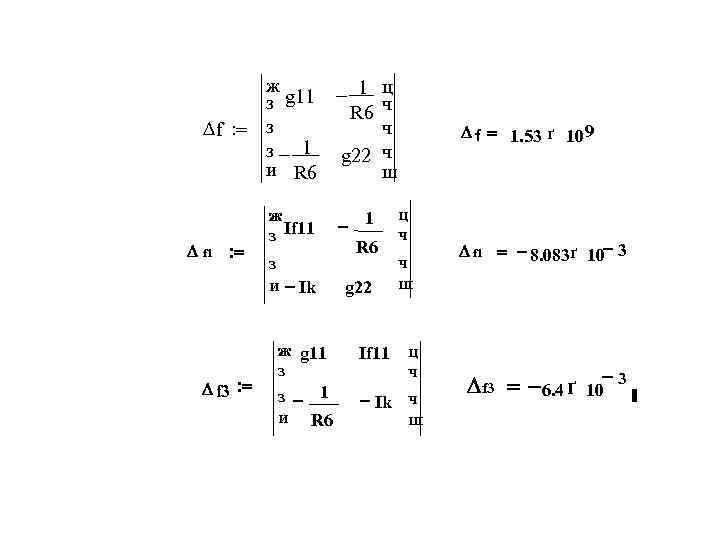ж з g 11 - 1 ц R 6 ч D f : = з ч D f = 1. 53 ґ 109 з - 1 g 22 ч и R 6 ш ж 1 ц з If 11 - ч D f 1 : = R 6 D f 1 = - 8. 083ґ 10 - 3 з ч и - Ik g 22 ш ж g 11 If 11 ц з ч -3 D f 3 : = з - 1 Df 3 = -6. 4 ґ 10 - Ik ч и R 6 ш

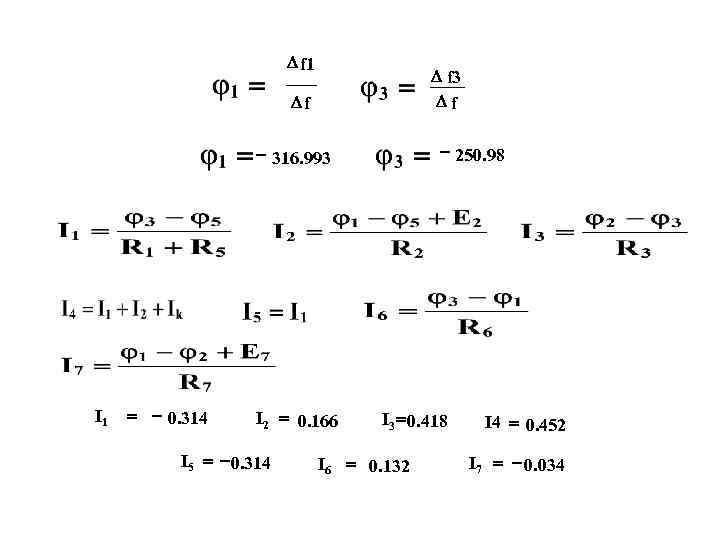D f 1 D f 3 Df - 316. 993 - 250. 98 I 1 = - 0. 314 I 2 = 0. 166 I 3 = 0. 418 I 4 = 0. 452 I 5 = - 0. 314 I 6 = 0. 132 I 7 = - 0. 034

Метод эквивалентного генератора

Порядок расчета электрических цепей методом эквивалентного генератора 1. Расставляем условно- положительные направления токов в электрической цепи. 2. Обрываем электрическую цепь в интересующей нас ветви. 3. Произвольно выбираем в месте обрыва направление вектора Uхх. 4. Любым известным методом расчета электрических цепей постоянного тока определяем величину Uхх( Еэг ). [При этом, во всех ветвях активного двухполюсника, кроме оборванной, протекают токи холостого хода]. 5. Полагая, что все источники питания в электрической цепи, равны нулю (Ек=0; Iк=0. ), отыщем полное сопротивление цепи относительно зажимов оборванной ветви. Это и есть внутреннее сопротивление эквивалентного генератора (Rвн) или входное сопротивление пассивного двухполюсника. 6. Ток в ветви с сопротивлением нагрузки определяем по формуле

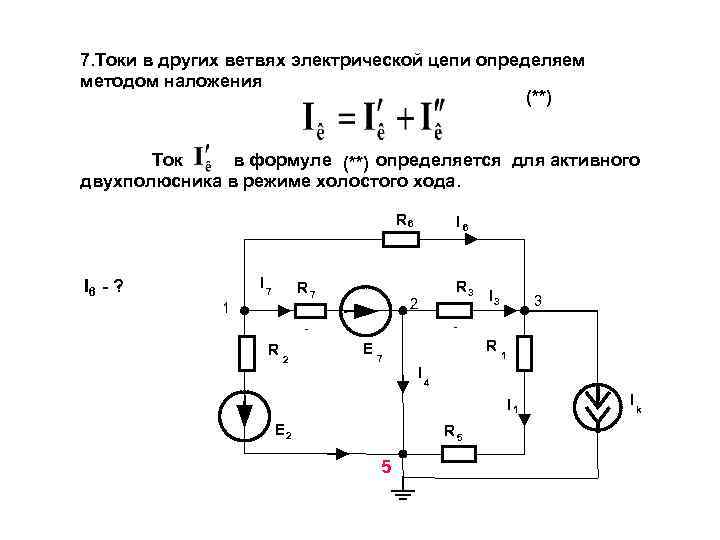7. Токи в других ветвях электрической цепи определяем методом наложения (**) Ток в формуле (**) определяется для активного двухполюсника в режиме холостого хода. R 6 I 6 - ? I R 7 R 3 7 I 3 3 1 2 R E R 2 7 1 I 4 I 1 I k E 2 R 5 5

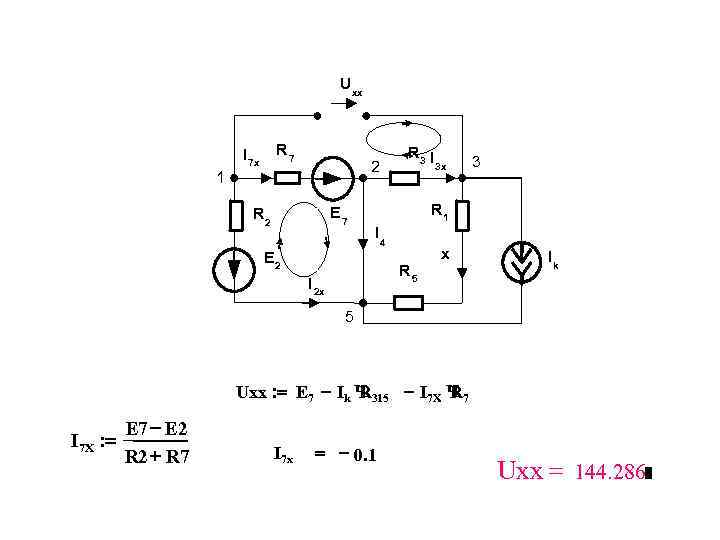Uхх I 7 х R 7 R 3 I 2 3 х 3 1 R 2 E 7 R 1 I 4 E 2 х Ik R 5 I 2 х 5 Uxx : = E 7 - Ik Ч 315 - I 7 Х Ч 7 R R E 7 - E 2 I 7 Х : = R 2 + R 7 I 7 x = - 0. 1 Uxx = 144. 286

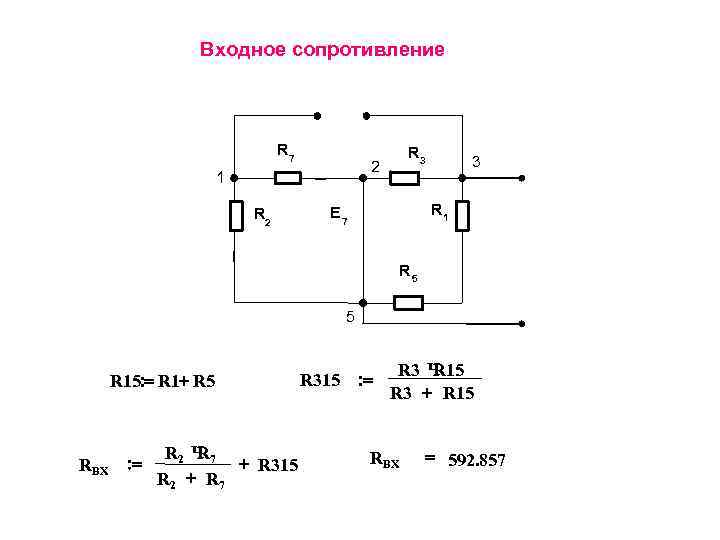Входное сопротивление R 7 R 3 2 3 1 R 2 E 7 R 1 R 5 R 3 Ч R 15: = R 1+ R 5 R 315 : = R 3 + R 15 R 2 Ч 7 R RBX = 592. 857 RBX : = + R 315 R 2 + R 7

Uxx I 6 = 0. 132 I 6 : = R 6 + RBX Метод наложения Порядок расчета цепи методом наложения 1. Расставляем положительные направления истинных токов в ветвях 2. Поочередно оставляем в цепи по одной ЭДС. Остальные ЭДС при этом равны нулю, но их внутренние сопротивления оставлены. 3. Находим частичные токи в ветвях цепи от каждой ЭДС в отдельности. Линейные электрические цепи постоянного тока

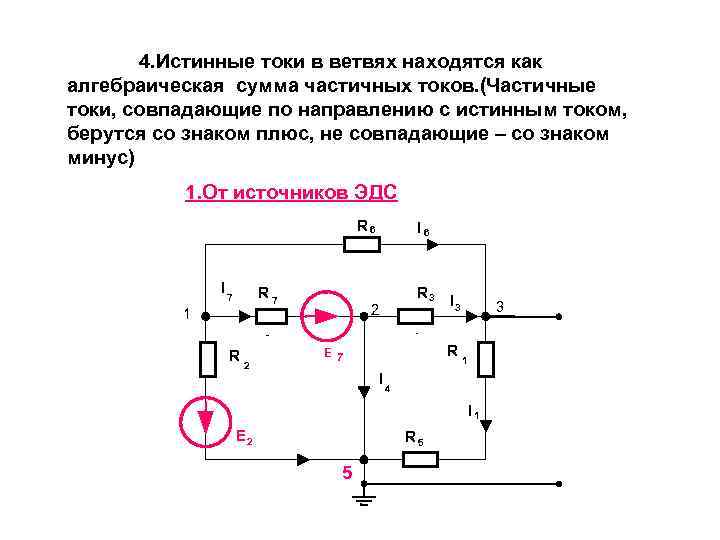4. Истинные токи в ветвях находятся как алгебраическая сумма частичных токов. (Частичные токи, совпадающие по направлению с истинным током, берутся со знаком плюс, не совпадающие – со знаком минус) 1. От источников ЭДС R 6 I 6 I R 7 R 3 7 I 3 3 1 2 R E 7 R 2 1 I 4 I 1 E 2 R 5 5

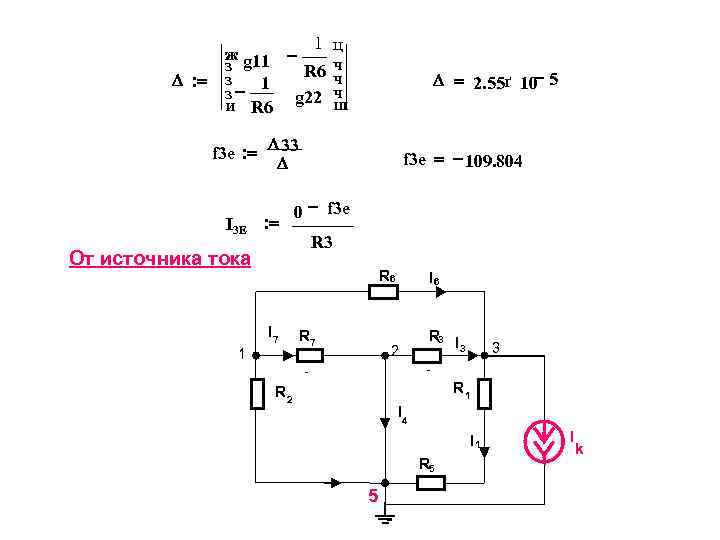1 ц ж g 11 - з R 6 ч D : = з 1 ч D = 2. 55ґ 10 - 5 з- ч и R 6 g 22 ш f 3 e : = D 33 f 3 e = - 109. 804 D 0 - f 3 e I 3 E : = R 3 От источника тока R 6 I 6 I 7 R 7 R 3 I 1 2 3 3 R 2 R 1 I 4 I 1 I k R 5 5

Ч Rek 1 R 15 Rek 2: = Rek 1= 750 Rek 1+ R 15 Rek 2= 387. 097 Rek 2 I 3 i: = Ik. Ч I 3 i = 0. 235 Rek 2+ R 3 I 3 : = I 3 i+ I 3 E I 3 = 0. 418

Баланс мощностей – равенство генерируемых и потребляемых в электрической цепи мощностей ( закон сохранения энергии в электрической цепи). Jk-ток источника тока Uk- напряжение на источнике тока

Рпот = I 1 2 Ч 1 + I 2 2 Ч 2 + I 3 2 Ч 3 + I 4 2 Ч + I 5 2 Ч 5 + I 6 2 Ч + I 7 2 Ч 7 = 206. 797 R R 0 R 6 R Pген : = E 2 Ч 2 + E 7 Ч 7 + ( f 5 - f 3 ) Чk I I Pген = 206. 797