Методы получения тонких пленок ВОПРОСЫ t t

Методы получения тонких пленок

ВОПРОСЫ t t t t t 1. Конденсация тонких пленок 2. Адатом 3. Кластер 4. Коэффициент конденсации 5. Коэффициент аккомодации 6. Две модели образования зародышей тонкой пленки 7. Среднее время релаксации и жизни адатома 8. Заполнение поверхности подложки 9. Средняя длина диффузионного пробега

Методы испарения (осаждения) - Вакуумное испарение - Ионная бомбардировка (ионное распыление) - Химическое осаждение - Электрохимическое осаждение - Ионное осаждение - Анодирование

Вакуумное термодиффузионное осаждение тонких пленок t t t t 1857 год Фарадей [Faraday M. , Phil. Trans. , 147, 145 (1857)] - взрыв металлических проволочек в инертной атмосфере 1887 год Нарволд [Nahrwold R. , Ann. Physik, 31, 467 (1887)] - осаждение тонких металлических пленок в вакууме 1888 год Кундт [Kundt A. , Ann. Physik, 34, 473 (1888)] – использование этих пленок в оптике для определения показ. преломления металлов Вакуумное осаждение тонких пленок есть совокупность нескольких процессов: - переход вещества из конденсированной фазы (твердой или жидкой) в газообразную; - перенос паров вещества в пространстве от испарителя до подложки при пониженном давлении газа; конденсация паров вещества при достижении подложки.

Вакуумное термодиффузионное напыление t t t Определения: 1. Адатомом называется атом находящийся в физически адсорбированном состоянии, но не успевший прийти в термодинамическое равновесие с поверхностью 2. Кластером называется устойчивое образование из нескольких провзаимодействовавших посредством Ван дер Ваальсовых сил друг с другом адатомов

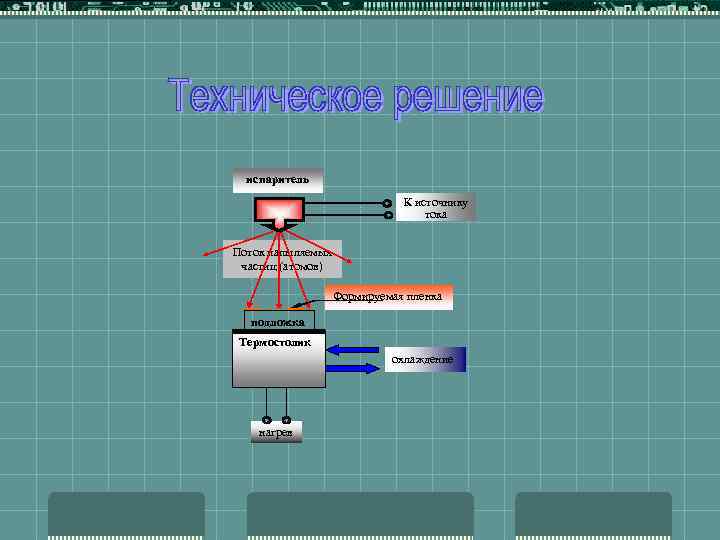испаритель К источнику тока Поток напыляемых частиц (атомов) Формируемая пленка подложка Термостолик охлаждение нагрев

t t t Вероятность того, что атом будет захвачен поверхностью называют коэффициентом конденсации или коэффициентом соударения. Его измеряют отношением числа атомов сконденсировавшегося на поверхности материала к общему числу атомов, ударившихся о поверхность. Степень термического равновесия описывают коэффициентом аккомодации Т, который определяется следующим образом: Т = (TI - TR)/(TI – TS) = (EI - ER)/(EI – ES), где T и E соответственно эквивалентные среднеквадратичные температуры и кинетические энергии падающих ( I ) и отраженных, вновь испарившихся, атомов пучка ( R ) и подложки ( S ).

t t t t Среднее время релаксации е, необходимое для того чтобы атом пришел в термическое равновесие с подложкой, должно быть меньше 2/ , где - частота колебаний адатома на поверхности. Среднее время жизни адатома на поверхности до десорбции определяется следующим образом: S = (1/ )exp(Qдес/k. T), следовательно е ~ 2 S exp(-Qдес/k. T).

t За период жизни в адсорбированном состоянии адатом мигрирует по поверхности со средней длиной диффузионного пробега Ā, определяемой броуновским движением по формуле Эйнштейна: t t Ā = (2 Ds s)1/2 = (2 s)1/2 a exp(-Qдес/2 k. T) = 21/2 a exp[(Qдес - Qдиф)/2 k. T], t t Где а – расстояние перескока между адсорбционными узлами поверхности, Qдиф – энергия активации перескока при поверхностной диффузии, а коэффициент поверхностной диффузии равен t а 2 exp(- Qдиф/k. T).

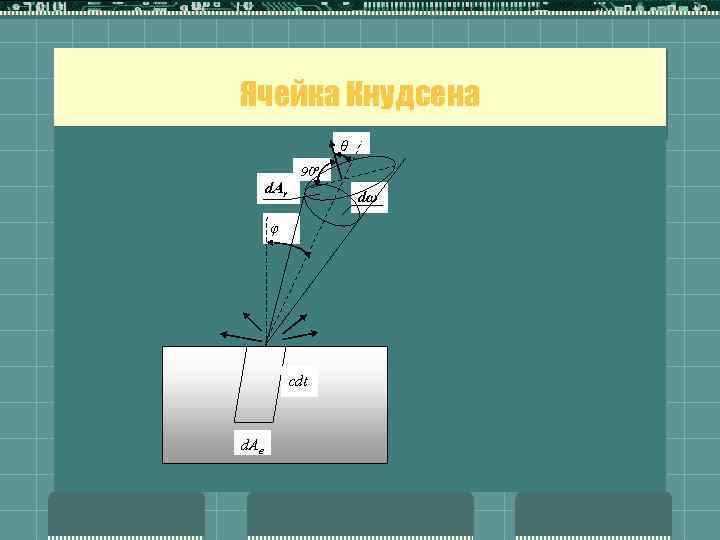Ячейка Кнудсена θ d. Ar 90 o dω φ cdt d. Ae

Допущения модели t 1. Ячейка Кнудсена состоит из изотермической оболочки с бесконечно малым отверстием d. Ae и с бесконечно тонкими стенками. t 2. В ячейке содержится N молекул, скорости которых распределены по Максвелловскому закону

t t t t 3. Молекулы сталкиваются со стенками оболочки и отражаются от них, причем характер распределения скоростей не изменяется. 4. Молекулы, движущиеся к отверстию, покидают ячейку в том же направлении и с той же скоростью, которую они имели непосредственно перед выходом 5. Общее число молекул внутри ячейки остается постоянным. 6. в потоке испаряемого вещества будет определяться распределением молекул по скоростям внутри эффузионной ячейки 7. Распределение скоростей молекул может быть описано выражением для числа молекул внутри малого пространственного угла dω при данном направлении движения. 8. Направление движения определяется углом φ по отношению к нормали к элементу поверхности d. Ae 9. Пусть молекулы обладают скоростью «c» .

t Полное число таких молекул внутри ячейки составляет t d. Nc = NΦ(c 2)dc. t За время dt смогут достигнуть элемента поверхности d. Ae и покинуть ячейку в направлении φ только те молекулы, которые заключены внутри наклонной призмы t Эти молекулы составляют часть общего числа молекул, равную cdt cosφAe/V t часть этих молекул равная t (dω/4π) t будет двигаться в направлении к d. Ae. Тогда число молекул, имеющих скорость с и покидающих ячейку в направлении φ, можно записать в виде t d 4 Ne, c(φ) = (N/V)c. Ф(c 2)dc d. Ae dt cosφ ,

t t t Интегрирование по всем скоростям даст полное число молекул, находящихся внутри угла dω t d 3 Ne(φ) = 0. 25(N/V)cd. Ae dt cosφ(dω/4π) Масса молекул равна t d 3 Me(φ) = md 3 Ne(φ) и, поскольку m(1/4)(N/V)c = Г, то можно записать t d 3 Me(φ) = Гd. Ae dt cosφ(dω/4π) или после подстановки величины общего количества испаренного вещества имеем t d. Me(φ) = Mecosφ(dω/4π) Последние два уравнения представляют собой косинусоидальный закон распределения, который эквивалентен закону Ламберта в оптике. В соответствии с этим законом испарение вещества происходит неравномерно во всех направлениях, а преимущественно в направлениях близких к нормали к испаряемой поверхности, где cosφ имеет максимальную величину.

t. Две tосновных модели образования зародышей из паровой фазы: t tкапиллярная и атомная модели t.

t Капиллярная модель постулирует: t для того, чтобы из пересыщенного пара образовалась конденсированная фаза (устойчивые островки конденсированной фазы) необходимы положительные флуктуации свободной энергии, приводящие к преодолению активационного барьера.

t. Предсказание модели: t изменение свободной энергии при образовании зародыша имеет МАКСИМУМ. t Т. е. зародыш по мере роста проходит через критический размер. Максимум свободной энергии получается в результате конкуренции двух параметров: очень большого отношения поверхности к объему в малых зародышах, изза которого их устойчивость уменьшается, и наличия энергии конденсации, увеличивающей устойчивость зародышей с увеличением их размеров (См. следующий слайд) t капиллярная модель даёт значения радиусов зародышей < 5 Å, а иногда и того меньше !?

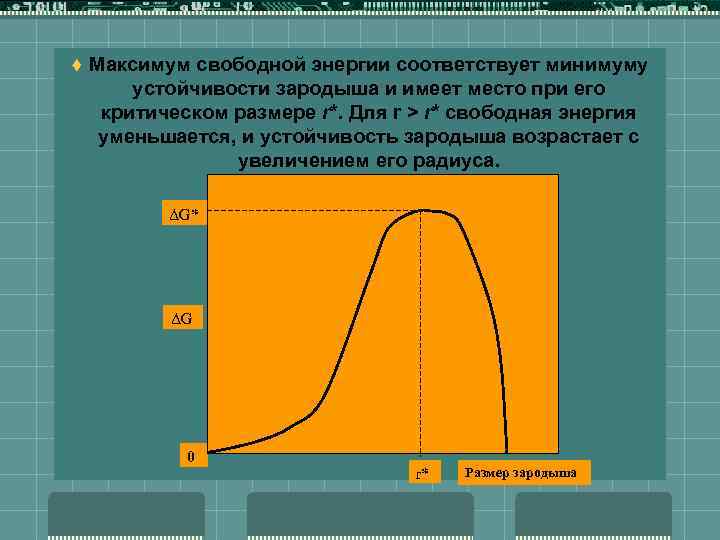t Максимум свободной энергии соответствует минимуму устойчивости зародыша и имеет место при его критическом размере r*. Для r > r* свободная энергия уменьшается, и устойчивость зародыша возрастает с увеличением его радиуса. ΔG* ΔG 0 r* Размер зародыша

Теория малых зародышей t Уолтон и Родин [Walton D. , J. Chem. Phys. 37, 2182 (1962)] описали метод, в котором противоречие капиллярной модели было снято. Они вместо изменения свободной энергии предложили использовать потенциальную энергию – энергию диссоциации зародыша, содержащего i атомов в n зародышах

[Sigsbee R. A. , Pound G. M. Advan. Coll. Interf. Sci. , 1, 335 (1967)] t Более поздние исследования показали, что обе теории основываются на одинаковых концепциях и они совпадают при определенном выборе поверхностной энергии конденсата и энергии адсорбата отдельного атома. Основная РАЗНИЦА между моделями состоит в том, что модель малых зародышей рассматривает только дискретное расположение атомов, в то время как капиллярная модель рассматривает простую идеализированную форму зародыша. При этом капиллярная модель предсказывает непрерывные изменения размера критического зародыша и скорости зародышеобразования. Согласно модели малых зародышей эти изменения происходят скачком.