МЕТОДЫ ОПТИМИЗАЦИИ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ МЕТОДЫ ОПТИМИЗАЦИИ

МЕТОДЫ ОПТИМИЗАЦИИ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ.

МЕТОДЫ ОПТИМИЗАЦИИ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ В конечном счете, целью моделирования ХТП является его лучшая реализация или его оптимизация. Человек всегда старался организовать свою деятельность так, чтобы результаты ее были наилучшими. Раньше задачи оптимизации отдельных производств решались изолированно друг от друга. И часто вопрос об оптимальном варианте производства решался интуитивно на основании опыта исследователя, проектировщика, технолога.

Частично это можно объяснить большой сложностью технологических процессов, множеством взаимосвязей в каждом процессе. Т. к. для эффективного решения задачи оптимизации необходимо оценить влияние всех этих факторов и сравнить громадное количество возможных вариантов организации технологии. На основании традиционных методов такая оценка отсутствовала, и оптимизация была неэффективной. И часто на стадии разработки выбирался далеко не самый лучший результат, и после пуска производства начинались переделки и поиски путей улучшения процессов. Только с развитием кибернетики и появлением быстродействующих ЭВМ начала формироваться оптимизация, как научное направление, с едиными методами, которые могут применяться в различных областях техники.

Оптимизация – это целенаправленная деятельность людей, которая заключается в получении наилучших результатов при соответствующих условиях. Оптимизация заключается в нахождении оптимума рассматриваемой функции или оптимальных условий проведения технологического процесса. Для оценки оптимума необходимо, прежде всего, выбрать критерий оптимизации. Критерием оптимальности (оптимизации) называется количественная оценка оптимизируемого качества объекта. Это главный признак, по которому судят о том, насколько хорошо функционирует данная система, работает данный процесс.

В зависимости от конкретных условий в качестве критерия оптимальности можно выбрать технологический критерий (например, максимальный выход продукции с единицы объема аппарата), а также экономический критерий (например, минимальная стоимость продукта при заданной производительности).

Требования к критерию оптимальности 1. Критерий оптимальности должен быть единственным. 2. Критерий оптимальности должен выражаться числом. Оптимизация по критерию красоты не может быть.

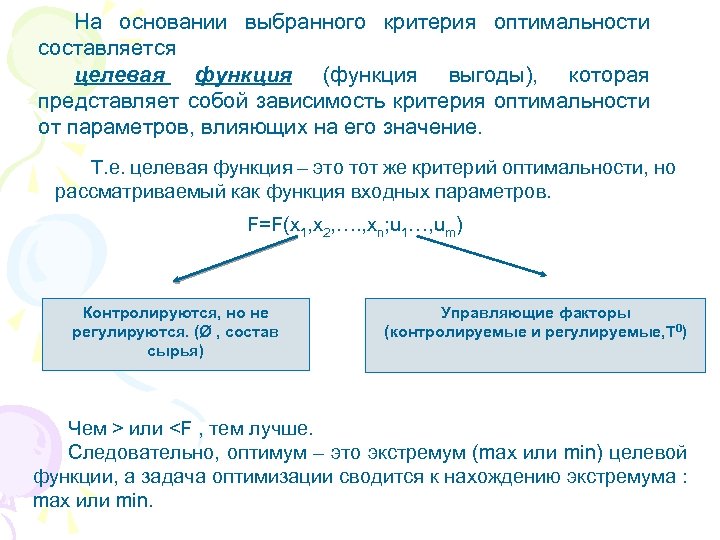На основании выбранного критерия оптимальности составляется целевая функция (функция выгоды), которая представляет собой зависимость критерия оптимальности от параметров, влияющих на его значение. Т. е. целевая функция – это тот же критерий оптимальности, но рассматриваемый как функция входных параметров. F=F(x 1, x 2, …. , xn; u 1…, um) Контролируются, но не регулируются. (Ø , состав сырья) Управляющие факторы (контролируемые и регулируемые, Т 0) Чем > или

Оптимизирующие параметры- это те из входных параметров системы, которые в процессе оптимизации относят к управляющим и которые применяются для оптимизации процесса. Ограничения - это условия, которые необходимо соблюдать независимо от того, как их соблюдение повлияет на величину критерия оптимальности. Примеры возможных ограничений: • • По количеству и качеству сырья и продукции. По условиям технологии: а) например, в качестве управляющего параметра выбрана t 0. Она не может быть выше той, при которой портится катализатор. б) не можем менять размер аппарата.

• По экономическим соображениям (капитальные затраты не должны превышать выделенной суммы). • По вопросам охраны труда и окружающей среды. По математическим признакам ограничения разделяют на: ограничения типа равенств, которые устанавливают определенные значения того или иного фактора xi=ai (например, задаются значения по составу сырья, размеры аппарата и т. д. ) ограничения типа неравенств, которые пределы изменения параметров процесса. определяют Например: fi ai (производительность не ниже заданной). al fl bl (температура в пределах); fk bk (t 0 не выше той, которая выдержит материал)

Постановка задачи оптимизации состоит в следующем: 1. Необходимо создать математическую модель объекта оптимизации. 2. Выбрать критерий оптимальности, оптимизирующие параметры и сформировать функцию цели. 3. Установить возможные ограничения, которые должны накладываться на переменные. 4. Выбрать метод оптимизации, который позволит найти экстремальное значение искомых величин.

СИСТЕМАТИЗАЦИЯ МЕТОДОВ ОПТИМИЗАЦИИ Выбор того или иного метода в значительной степени определяется постановкой задачи оптимизации, а также математической моделью объекта оптимизации. Методы оптимизации: • Аналитические. а) Методы исследования функций классического анализа. Применяются для детерминированных процессов с критерием оптимальности в виде дифференцируемых функций. б) Метод множителей Лагранжа – для задач с ограничениями типа равенств с критерием оптимальности в виде дифференцируемых функций. в) Вариационные методы – для задач с критерием оптимальности в виде функционала. г) Принцип максимума.

• Методы математического программирования. а) динамическое программирование; б) нелинейное программирование; в) линейное программирование; • • Градиентные. Статистические. При составлении программ с использованием методов оптимизации нужно придерживаться модульного принципа, т. к. требуется многократное обращение к расчету целевой функции.

СТАТИСТИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ. Наиболее сложен для оптимизации случай, когда неизвестен вид целевой функции. В этом случае оптимум находят экспериментально. Существует 2 области изменения выходного параметра y: Область, удаленная от оптимума, в которой происходит значительное изменение y. Почти стационарная область, в которой практически не происходит изменения y. После того как область, удаленная от оптимума, описана адекватным линейным уравнением, используем его для оптимизации. Рассмотрим метод Бокса-Уилсона • •

МЕТОД БОКСА-УИЛСОНА. (крутое восхождение по поверхности отклика) Используя факторное планирование, в 1951 году Бокс и Уилсон предложили метод поиска оптимальных условий для сложных процессов. Постановка задачи оптимизации: Определить координаты оптимальной (экстремальной) точки (x 1 опт. , x 2 опт. , …xnопт. ) поверхности отклика y=f(x 1…xn).

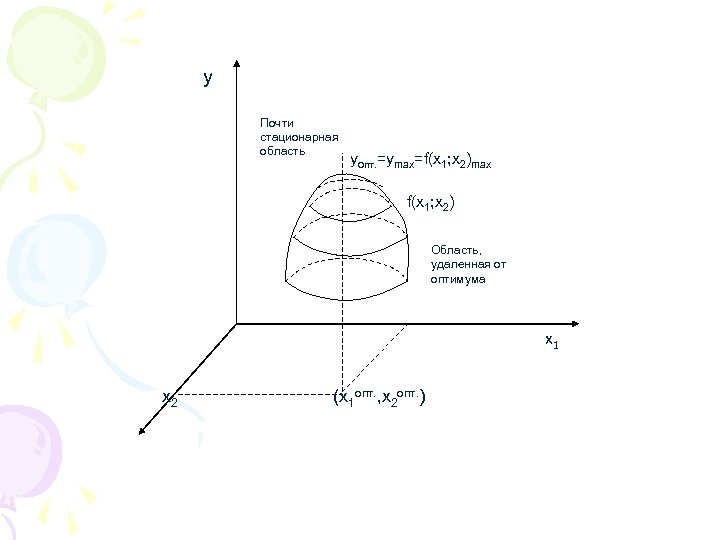y Почти стационарная область yопт. =ymax=f(x 1; x 2)max f(x 1; x 2) Область, удаленная от оптимума x 1 x 2 (x 1 опт. , x 2 опт. )

Метод градиента предусматривает движение к оптимуму по наикратчайшему пути, т. е. это движение к экстремуму по градиенту. Градиент – это вектор, который направлен в сторону наибыстрейшего изменения функции. . Пусть находимся в т. М. В этой точке ставится эксперимент по схеме ПФЭ или ДФЭ планирования для локального описания поверхности отклика в окрестности т. М, линейным уравнением регрессии.

Далее по этой поверхности отклика движемся по градиенту к экстремуму до тех пор, пока движение по этой плоскости обеспечивает рост y. Как только y перестает расти, переносят центр планирования в эту точку (до которой дошли по градиенту), выполняют эксперимент и опять строят плоскость. Все это (эта процедура) продолжается до тех пор, пока не попадем в почти стационарную область, т. е. близкую к экстремуму. В этой области ставится большой эксперимент для описания этой области полиномом 2 -ого порядка, а затем, полученная поверхность исследуется для локализации экстремума.

Шаг по каждой оси дает нам частная производная по переменным x 1 и x 2. т. к. то, следовательно, для того, чтобы двигаться по плоскости в направлении градиента, необходимо делать шаги пропорционально коэффициентам. При постановке опытов величина шага должна быть приблизительно равна произведению коэффициентов bi на интервал варьирования xi. grad f=b 1 x 1+b 2 xi – интервал варьирования по каждой переменной. bi xi – шаг по соответствующей оси.

Расчет «шагов» при движении по градиенту: 1. Вычисляют произведение коэффициентов регрессии на соответствующие интервалы варьирования факторов bi xi и фактор, для которого это произведение максимально, принимают за базовый. (bi xi)max=a 2. Для базового фактора выбирают шаг варьирования крутого восхождения ha, оставляя старый интервал варьирования xi, либо вводя новый – более мелкий. 3. Производят расчет шага для каждого фактора по уравнению: где коэффициенты берутся со своими знаками. Таким образом, знак шага по каждому фактору совпадает со знаком соответствующего коэффициента. Рассчитанные шаги по каждому фактору округляются.

Движение начинают от основного уровня. При первом шаге, т. е. опыте, факторы получают значения равные основному уровню плюс, рассчитанные шаги варьирования При каждом последующем шаге значения факторов изменяют на величину шага варьирования. Движение продолжают до тех пор, пока наблюдается увеличение (или уменьшение) функции отклика (улучшение). xi =x 0 +hi Пример: Методом крутого восхождения максимальный выход продукта D по реакции A K 1 получить D K 2 В качестве независимых параметров выбираются концентрация A - x 1 и температура – x 2.

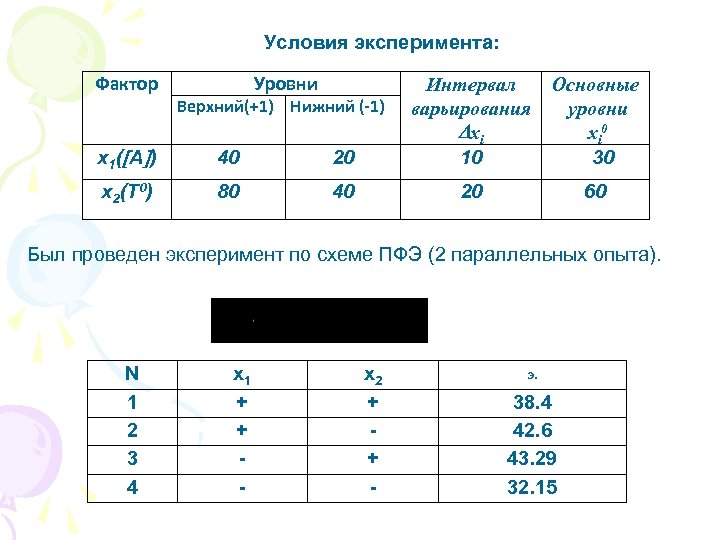Условия эксперимента: Фактор Уровни x 1 ( А ) 40 20 Интервал варьирования xi 10 x 2(T 0) 80 40 20 Верхний(+1) Нижний (-1) Основные уровни xi 0 30 60 Был проведен эксперимент по схеме ПФЭ (2 параллельных опыта). N 1 2 3 4 x 1 + + - x 2 + + - э. 38. 4 42. 6 43. 29 32. 15

1. По критерию Кохрена проверялась дисперсия на однородность. 2. Определялась дисперсия воспроизводимости. 3. Определялись коэффициенты уравнения регрессии и проверялись на значимость по критерию Стьюдента. Уравнение запишется: 4. Проверка на адекватность по критерию Фишера и показала, что уравнение адекватно, а, следовательно, может быть использовано для оптимизации

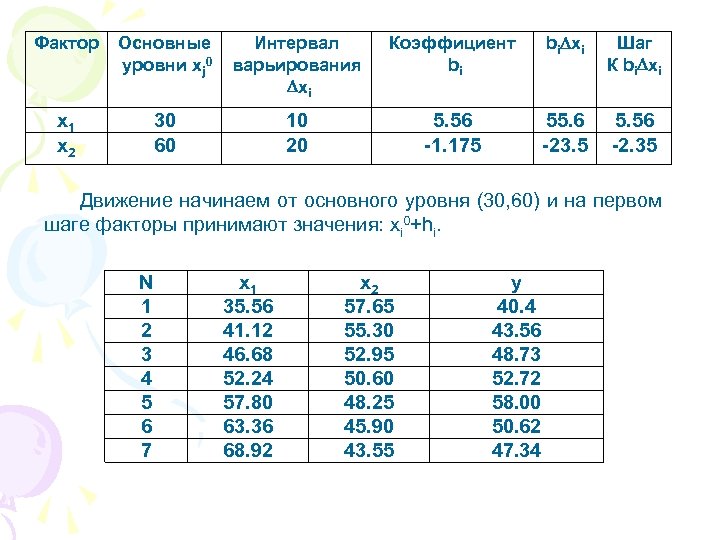Фактор Основные уровни xj 0 Интервал варьирования xi Коэффициент bi bi xi Шаг К bi xi x 1 x 2 30 60 10 20 5. 56 -1. 175 55. 6 -23. 5 5. 56 -2. 35 Движение начинаем от основного уровня (30, 60) и на первом шаге факторы принимают значения: xi 0+hi. N 1 2 3 4 5 6 7 x 1 35. 56 41. 12 46. 68 52. 24 57. 80 63. 36 68. 92 x 2 57. 65 55. 30 52. 95 50. 60 48. 25 45. 90 43. 55 y 40. 4 43. 56 48. 73 52. 72 58. 00 50. 62 47. 34

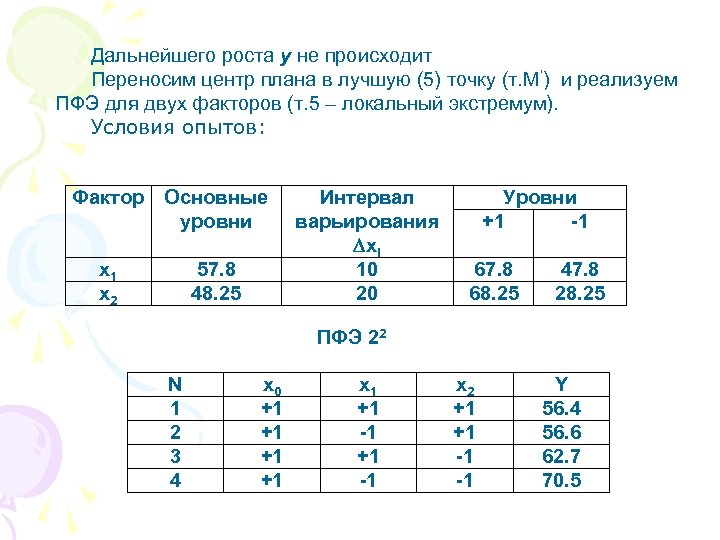Дальнейшего роста y не происходит Переносим центр плана в лучшую (5) точку (т. М’) и реализуем ПФЭ для двух факторов (т. 5 – локальный экстремум). Условия опытов: Фактор Основные уровни x 1 x 2 57. 8 48. 25 Интервал варьирования xi 10 20 Уровни +1 -1 67. 8 68. 25 47. 8 28. 25 ПФЭ 22 N 1 2 3 4 x 0 +1 +1 x 1 +1 -1 x 2 +1 +1 -1 -1 Y 56. 4 56. 6 62. 7 70. 5

Вновь проводим регрессионный анализ. В результате получаем, что уравнение регрессии неадекватно эксперименту. Следовательно, достигли области близкой к экстремуму (почти стационарная область). Если бы уравнение вновь было адекватным, то от основного уровня вновь бы продолжали двигаться по градиенту (но шаги в этом случае делаются меньшими, т. к. приближении к оптимуму кривизна поверхности возрастает).