Методы оптимизации в теории управления Глава 1

Методы оптимизации в теории управления

Глава 1. Задачи конечномерной оптимизации в теории управления 1. 1. Основные понятия теории управления

Обычно в учебных курсах по теории управления рассматриваются некоторые специальные разделы этой теории, такие как теория автоматического управления или математическая теория оптимальных процессов, основанная на принципе максимума Понтрягина или принципе оптимальности Беллмана. В данном же случае нас будет интересовать управляемая система как некая общая концепция кибернетики — науки об управлении.

Под управлением будем понимать процесс такого воздействия на некоторую систему или объект (объект управления), при котором состояние системы или объекта изменяется «в нужную сторону» . Объектами управления, очевидно, могут быть: техническое устройство (например, автомобиль), экономическая ситуация на предприятии или фирме, экосистема региона, процесс разработки программного проекта, сам программный проект и его характеристики и т. п. Предполагается, что мы можем не только оказывать воздействие на объект, но и оценивать результаты этого воздействия по некоторым заданным критериям. Например, критериями качества процесса разработки программного проекта могут служить время завершения проекта и его бюджет (стоимость разработки). Влиять на эти характеристики (управлять ими) мы можем, например, с помощью перераспределения ресурсов между отдельными работами, составляющими данный программный проект.

Общая схема процесса управления приведена на рис. 1. 1. Объект управления рассматривается как сколь угодно сложная система, преобразующая входные управляющие воздействия U(t) в выходные сигналы (траектории) V(t) , характеризующие состояние объекта управления в момент времени t. Очевидно, что реальный объект управления может иметь множество входов и выходов, определяющих его функциональное взаимодействие с внешней средой. Все эти каналы связи со средой на рис. 1. 1 не показаны. Изображены лишь те входы и выходы, которые являются существенными для формулирования задачи управления. Объект управления и воздействующее на него устройство управления образуют систему управления. Предполагается, что на объект управления действуют также возмущения ξ(t), изменяющие, как правило, в непредсказуемом направлении основные характеристики объекта управления.

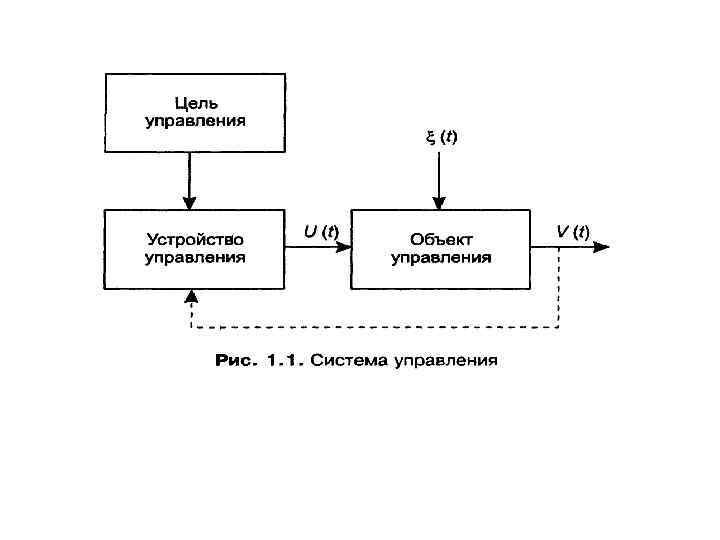
Мы здесь для определенности будем предполагать, что все функции времени, изображенные на рис. 1. 1, являются вектор-функциями с вещественными компонентами и заданными размерностями. Сигнал управления вырабатывается в соответствии с некоторой заданной целью управления, определяемой теми задачами, которые поставлены перед системой управления. Довольно часто в системах управления для выработки управляющих воздействий оказывается необходимой информация о действительном состоянии объекта управления. Эта информация поступает по цепи обратной связи, показанной на рис. 1. 1 пунктирной стрелкой.

В качестве примера объекта управления может выступать некоторый завод, перерабатывающий сырье в готовую продукцию. Здесь под управлением может пониматься вся система мероприятий и нововведений, направленная на достижение определенной цели или целей, связанных, например, с качеством и количеством выпускаемой продукции, а также, возможно, с определенными требованиями к срокам выпуска этой продукции.

Как справедливо указывается в литературе, описание некоторого объекта как объекта управления и выявление каналов воздействия на него может производиться только исходя из заданной цели управления. Так, например, тот же завод с точки зрения служб санэпиднадзора или иных экологических служб является объектом управления, перерабатывающим сырье в промышленные отходы, загрязняющие окружающую среду. В этом случае управление со стороны этих служб будет направлено на снижение влияния вредных техногенных факторов, а вовсе не на интенсификацию производства, как в первом случае.

Основные задачи, решаемые большинством систем управления и отражающие главные цели управления, могут быть отнесены к одному из следующих типов: стабилизация, выполнение программы, слежение, экстремальное управление, оптимизация.

Задача стабилизации заключается в поддержании некоторых выходных (управляемых) характеристик объекта управления на заданных уровнях несмотря на постоянно действующие возмущения ξ(t) : V(t) = const. Задачи стабилизации возникают и решаются в живой природе (поддержание стабильной температуры тела у теплокровных животных), в технических системах (например, стабилизация напряжения и частоты в энергосистемах вне зависимости от нагрузки) и т. д.

Задача выполнения программы, или задача программного управления, возникает, когда необходимо обеспечить наперед заданные траектории V(t). Иначе говоря, необходимо «заставить» объект управления изменять свои управляемые характеристики во времени по заданному закону, по определенной программе V*(t). Например, процесс разработки некоторого технического изделия на заводе должен протекать в соответствии с заранее разработанным временным графиком. Метаморфоза насекомых в живой природе также происходит в соответствии с некоторыми биологическими программами развития. Запускаемый космический аппарат обычно выводится на траекторию в соответствии с заранее заданной расчетной траекторией. Легко видеть, что задача стабилизации является частным случаем задачи программного управления.

В задачах слежения основная проблема сводится к формированию такой выходной траектории V(t). управляемого объекта, которая как можно более точно аппроксимировала бы другую, заранее не известную траекторию V*(t). Например, при управлении пушечной турелью оператор (наводчик орудия) при наводке на цель вращает легкие маховички (задавая траекторию V*(t)), а тяжелая пушечная турель отслеживает движение маховичков, изменяя, ориентацию ствола по углу и по азимуту (реализуя соответствующую траекторию V(t)). Аналогичные задачи слежения возникают, когда антенна радиолокатора отслеживает непредвиденные движения какого-либо летящего объекта. Число подобных примеров легко может быть увеличено.

Задачи экстремального управления, или, как иногда говорят, задачи настройки, возникают довольно часто. Они заключаются в достижении некоторой экстремальной цели, которая к тому же может эволюционировать во времени. Предполагается, что на траекториях объекта управления задан некоторый функционал, отражающий эту цель (обычно его экстремум соответствует некоторому нормальному, благоприятному или наилучшему режиму работы) и зависящий как от управляемых, так и от неуправляемых параметров объекта. Требуется с помощью соответствующих управляющих воздействий добиваться того, чтобы значение целевого функционала в любой момент времени находилось в достаточно малой окрестности экстремума (максимума или минимума — в зависимости от смысловой интерпретации).

Например, при настройке радиоприемника на какую-либо радиостанцию добиваются достижения максимальной громкости. Автоматические системы экстремального управления часто называются системами автоматической оптимизации, или самонастраивающимися системами. Задачи экстремального управления являются в определенном смысле более сложными, чем ранее перечисленные. Действительно, если, например, в задаче стабилизации достаточно одного измерения стабилизируемой величины для определения направления ее корректировки, то в данном случае для синтеза управляющего воздействия необходимо как минимум два поисковых измерения целевого функционала как основного выхода объекта. При настройке путем поиска — специальным образом организованных пробных движений — находится заранее не известное состояние объекта, соответствующее некоторому оптимальному режиму.

Важно отметить, что задачи экстремального управления являются не только более сложными, но и более общими. При необходимости практически любую задачу управления можно сформулировать на языке экстремального управления. Например, задачи стабилизации и программного управления могут быть сформулированы как задачи минимизации невязки (ошибки) между заданными и действительными выходными траекториями объекта. Другое дело — всегда ли оправданы такие формулировки? Это отдельный вопрос, и ответ на него однозначный — не всегда.

Когда мы говорим о задачах оптимизации в теории управления, то подразумеваем задачи реализации некоторых оптимальных (по заданному критерию) выходных траекторий управляемой системы. В частности, может ставиться задача перевода объекта управления из одной точки фазового пространства в другую, например, за минимальное время при соблюдении заданных ограничений, в том числе фазовых. Очевидно, такие задачи непосредственно не могут быть отнесены ни к одному из ранее рассмотренных типов задач (стабилизация, выполнение программы, слежение, настройка).

В качестве примера можно рассмотреть теперь уже ставший классическим пример задачи об оптимальном в смысле расхода горючего режиме набора высоты и скорости летательным аппаратом, например, самолетом [14]. На рис. 1. 2 показано фазовое пространство самолета как объекта управления. Ось абсцисс является осью высот H, а ось ординат — осью скоростей v. Состояние самолета изображается точкой фазового пространства — плоскости v 0 H.

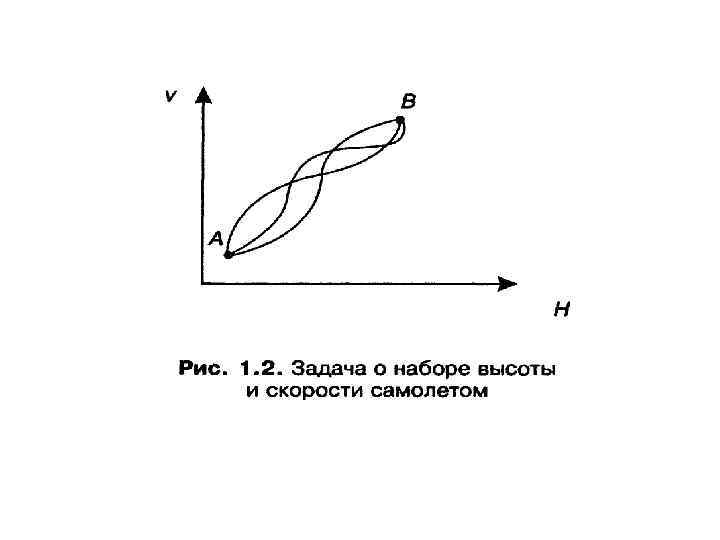
Существует множество траекторий в фазовом пространстве, соединяющих начальную (А) и конечную — целевую — точки (В). Требуется выбрать такое управление самолетом, чтобы набор высоты и скорости проходил в соответствии с некоторой оптимальной траекторией. Под критерием оптимальности в данном примере понимается суммарный расход горючего. Если такая оптимальная траектория рассчитана заранее, то она, в принципе, может выступать в качестве программы при последующем решении задачи программного управления. Однако обычно ситуация оказывается несколько сложнее. Может ставиться задача построения оптимального поведения объекта независимо от того, в какой точке фазового пространства он оказался в процессе реального движения в условиях возмущений. Собственно задача выполнения программы здесь уже не является определяющей.

Нужно ясно понимать, что все перечисленные задачи теории управления могут находиться в определенной иерархической взаимосвязи и присутствовать одновременно при проектировании той или иной системы управления. Например, на одном из иерархических уровней мы можем решать задачу стабилизации, строя соответствующую систему управления. В то же время (на более высоком уровне) может ставиться задача экстремального управления этой системой стабилизации в соответствии с некоторым критерием качества стабилизации и т. д. Число таких «вложений» теоретически не ограничено.

Еще раз отметим, что мы сейчас рассматривали основные задачи теории управления, а не методы их решения. Методы решения сформулированных задач и их реализация в виде конкретных систем управления могут быть различными, и они связаны с основными принципами управления.

Жесткое управление. Принцип жесткого (разомкнутого) управления предполагает отсутствие обратной связи в общей схеме управления (см. рис. 1. 1). Такие системы управления без обратной связи называются разомкнутыми. Чаще всего они применяются для целей программного управления. Принцип жесткого управления проиллюстрирован на рис. 1. 3, где представлена система жесткого управления, решающая задачу программного управления (задачу выполнения заданной программы). Здесь цель управления задает желаемую программу изменения состояния объекта во времени. Эта программа передается управляющему устройству для построения необходимого управления. В результате такого управления состояние объекта должно изменяться по закону. Система управления стремится обеспечить равенство для любого момента времени. Рассмотрим данный процесс жесткого управления подробнее.

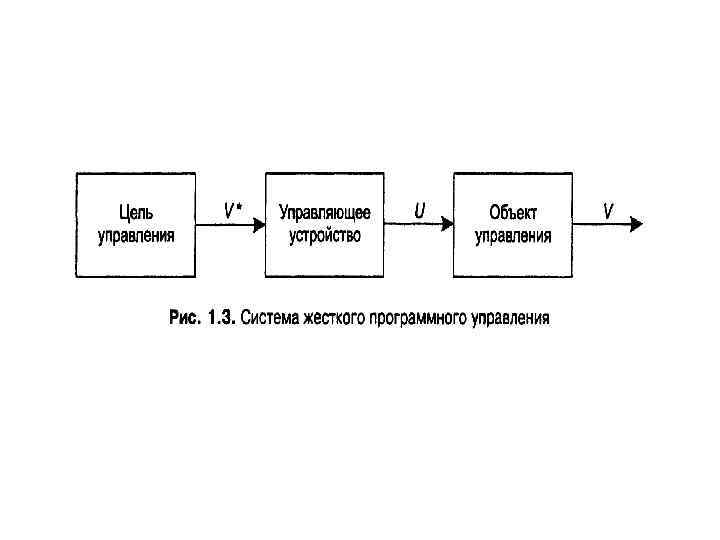
Здесь цель управления V*(t) задает желаемую программу изменения состояния объекта во времени. Эта программа передается управляющему устройству для построения необходимого управления U(t). В результате такого управления состояние объекта должно изменяться по закону V(t). Система управления стремится обеспечить равенство V(t) ≈ V*(t) для любого момента времени. Рассмотрим данный процесс жесткого управления подробнее.

Предположим, что объект управления является безынерционным и описывается оператором F: V(t) = F (U(t)) Предполагаем, что данное равенство справедливо для любого момента времени t. Управляющее устройство вырабатывает управляющее воздействие по закону U(t) = G (G (V*(t)) где G — оператор устройства управления. Очевидно, для достижения равенства V(t) = F (U(t)) = F(G (V*(t))) = V*(t) необходимо обеспечить закон управления G в виде G = F-1 Таким образом, оператор, характеризующий закон управления, является обратным к оператору объекта.

Существенные моменты в процессе жесткого управления сводятся к следующему. Во-первых, для построения закона управления необходимо иметь полную информацию об операторе объекта (математической модели объекта). Во-вторых, предполагается стабильность характеристик объекта, то есть неизменность его оператора. При малейших изменениях в объекте точность жесткого управления может быть нарушена.

Примером системы жесткого управления является система радиосвязи, когда акустические колебания V*(t) , создаваемые, например, диктором в студии, поступают с микрофона в управляющее устройство, где преобразуются в радиоволны U(t)(рис. 1. 4). После прохождения канала связи радиоволны попадают в приемник, детектируются, усиливаются и при помощи динамика преобразуются снова в акустические колебания. Здесь мы имеем факт управления на расстоянии колебаниями диффузора динамика таким образом, чтобы они копировали колебания в микрофонной цепи передатчика.

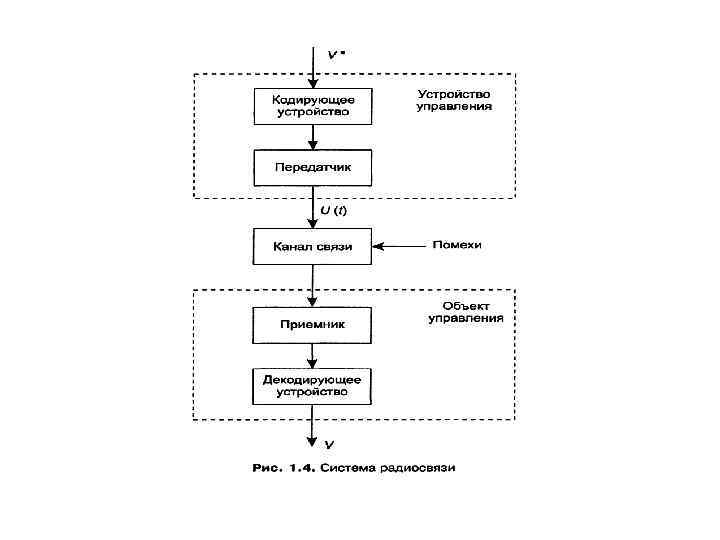
Таким образом, в системах жесткого управления управляющему устройству недоступна информация о действительном состоянии объекта управления — какая-либо обратная связь отсутствует. В гораздо большем числе случаев необходимо прибегать к более гибким принципам управления, оказывающимся более эффективными при наличии различных помех, возмущений и изменяющихся параметрах объекта управления.

Регулирование. В системах регулирования, в отличие от жесткого управления, управляющие воздействия строятся в зависимости от фактического текущего состояния объекта управления. Информация о состоянии объекта поступает по специально организованным каналам обратной связи. В этом случае говорят, что реализуется принцип замкнутого управления, а сама система управления называется замкнутой. Здесь так же, как и в предыдущем случае, для эффективного функционирования системы управления часто необходимо иметь модель (оператор) объекта управления. В противном случае построение управляющих воздействий оказывается невозможным или малоэффективным. Основное преимущество замкнутых систем перед разомкнутыми состоит в том, что они оказываются существенно менее зависимыми от неизмеримых возмущений и помех, особенно когда механизм влияния помех на объект управления неизвестен. Пример замкнутой системы программного управления представлен на рис. 1. 5.

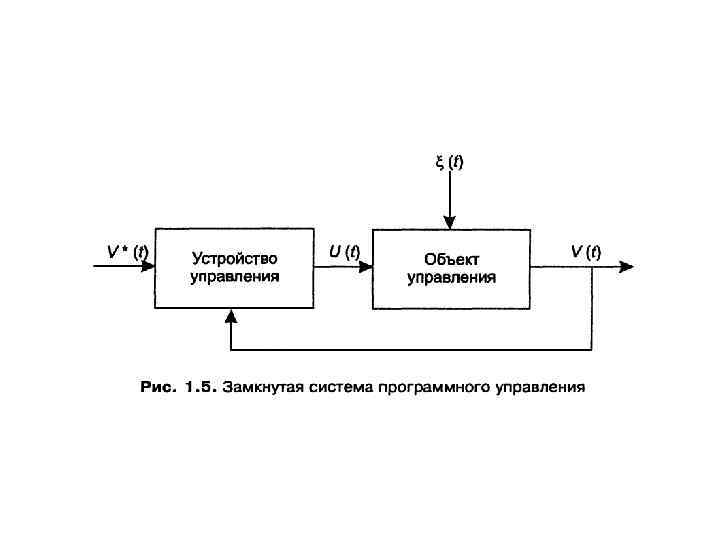
В устройстве управления сравнивается желаемое V*(t) и действительное значения функции V(t). Это позволяет определить, насколько состояние объекта отличается от требуемого (задаваемого программой V*(t) ). В результате управление строится как функция невязки: U(t) = f(V(t) – V*(t) Наличие обратной связи обычно позволяет существенно расширить возможности управления и ослабить требования к знанию структуры и свойств объекта управления.

Отметим, что все сложности управления начинаются при попытке управления сложным объектом. Управление простыми объектами обычно не вызывает каких-либо проблем. Например, система управления подогревательными приборами в помещении (или в аквариуме) может быть основана на очень простом принципе: включить подогрев, если температура ниже заданной, и выключить его, если температура выше или равна заданной. В этом случае не нужна никакая модель объекта управления.

Другое дело, что даже в этом простом примере нас могут интересовать возникающие при таком управлении колебания температуры. Для уменьшения этих колебаний мы можем начинать интересоваться мощностью нагревательного прибора, его инерционными свойствами, а также свойствами нагреваемой среды — в данном случае воды или воздуха. Например, существенным может оказаться учет нагреваемого объема воздуха или воды и т. д. Таким образом, нас уже интересует модель объекта управления.

Вообще, под сложной системой или объектом часто понимается система с антиинтуитивным поведением, то есть такая система, реакция которой на заданное входное воздействие или сигнал управления не может быть предсказана на основе «здравого смысла» . Мы, следовательно, отличаем сложную систему от большой системы, характеризуемой, например, числовыми массивами или файлами высокой размерности. В этом смысле большая система может быть и простой по поведению. Схема взаимодействия объекта управления с окружающей средой представлена на рис. 1. 6.

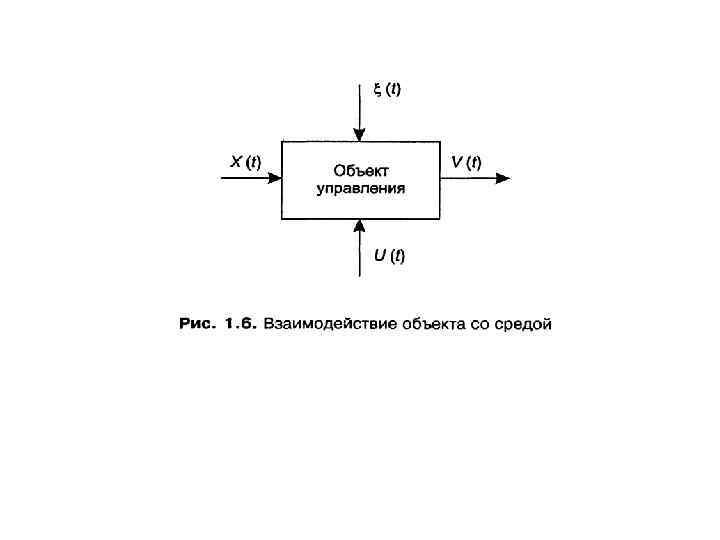
Здесь появился новый канал связи объекта со средой — X(t). Он означает неуправляемое, но наблюдаемое воздействие среды на объект. ξ(t) попрежнему означает вектор неуправляемых и ненаблюдаемых возмущений (как внутренних, так и внешних). Под оператором объекта управления F* будем понимать оператор , связывающий входы объекта с его выходом: V = F*(X, U, ξ )

Перечислим теперь характерные признаки сложности объекта управления. К ним в первую очередь относятся: • Отсутствие описания (в том числе алгоритмического) оператора F *. В то же время, как уже говорилось, для целей управления сложным объектом оно совершенно необходимо. • Неожиданное, антиинтуитивное поведение объекта. Иногда это поведение моделируется и объясняется с помощью введения фактора стохастичности. Поэтому для построения систем управления сложными объектами привлекается аппарат статистической или стохастической теории управления. • Нестационарность оператора F *. (изменчивость во времени)