Методы оптимизации Чернов Владимир Георгиевич

Методы оптимизации Чернов Владимир Георгиевич

• • • Лицо, принимающее решение (ЛПР), в сложных технических, экономических, социальных системах должно учитывать множество разнообразных факторов и уметь оценивать последствия их изменения. Важно, чтобы эти изменения не только приводили к лучшему результату, но и давали максимально полезный эффект. Целью оптимизации является выбор среди некоторого множества допустимых решений таких, которые можно было бы в том или ином смысле квалифицировать как оптимальные. При этом допустимост ь каждого решения понимается как возможность его фактического осуществления, а оптимальность как его целесообразность. Следует подчеркнуть, что оптимальное решение показывает предельные возможности системы и служит советом для ЛПР, а решение он может принять и другое, с учетом иного рода факторов, например политических, влияющих на экономическую ситуацию. Указанная проблема решается с помощью синтеза многих научных направлений, таких, как системный анализ и исследование операций, моделирование экономических систем, методы оптимизации функций и теории оптимального управления, теории игр и др.

• • • Сущность задач поясним, вводя основные определения и рассматривая простой пример принятия решения. Основные определения и постановка задачи: • система совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое для достижения доставленной цели; • операция способ достижения поставленной цели; оперирующая сторона участник операции, стремящийся к достижению поставленной цели; хi = 1, 2, … , хєХ, управляемые переменные, выбираемые из разрешенных способов действия оперирующей стороны Х; yj, =1, . . . , т, у є Y, неуправляемые переменные, относительно которых известно только множество Y (обычно это способы действия противоборствующей стороны); zk , к = 1, 2, …p, z є Z, случайные переменные, относительно которых известны только вероятностные характеристики со значениями, принимаемыми из области Z (например, плотность вероятности f(z)); критерий эффективности функция F(x, y, z), характеризующая степень достижения поставленной цели; стратегия операции х разрешенные способы действия оперирующей стороны; прямая задача исследования операций вычисление функции F(x, y, z) при конкретной стратегии ; обратная задача определение наилучшей стратегий х°, доставляющей минимум или максимум критерию эффективности операции При решении этих задач переменные y и z оказываются неопределенными. Наиболее часто для преодоления этой трудности используют следующие принципы: • максимального правдоподобия принимают такое значение переменных z, которое соответствует • наиболее вероятному, определяемому по плотности f(z).

• Байеса вычисляют математическое ожидание критерия эффективности • гарантированных оценок определяют наихудшую для оперирующей стороны оценку критерия эффективности: нижнюю для задачи максимизации критерия и верхнюю для задачи минимизации: Пример. Объединение ведет строительство завода. Необходимо выполнить следующие работы: А строительство корпусов; В разработка модели изделия; С наем и обучение рабочей силы; D монтаж оборудования; Е - отладка модели изделия. Время выполнения работ t. A = 2, t. B = 1, a tc, t. D, t. E принимают значения 2, 3, 4 с равной вероятностью. В зависимости от времени ввода завода в строй определяется прибыль (табл. В. 1). Таблица В. 1 Прибыль по годам ВРЕМЯ, Т 3 4 5 6 7 ПРИБЫЛЬ, F 120 ПО 100 50 0 В распоряжении оперирующей стороны имеется денежный резерв R = 20, который позволяет ускорить строительство завода на 1 год. Стоит ли использовать резерв?

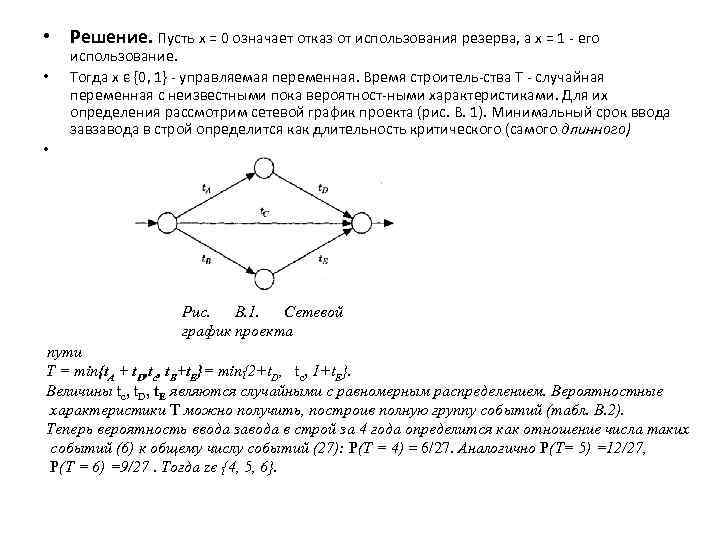• Решение. Пусть х = 0 означает отказ от использования резерва, а х = 1 его • использование. Тогда х є {0, 1} управляемая переменная. Время строитель ства Т случайная переменная с неизвестными пока вероятност ными характеристиками. Для их определения рассмотрим сетевой график проекта (рис. В. 1). Минимальный срок ввода завзавода в строй определится как длительность критического (самого длинного) • Рис. В. 1. Сетевой график проекта пути T = min{t. A + t. D, tc, t. B+t. E}= min{2+t. D, tc, 1+t. E}. Величины tc, t. D, t. E являются случайными с равномерным распределением. Вероятностные характеристики Т можно получить, построив полную группу событий (табл. В. 2). Теперь вероятность ввода завода в строй за 4 года определится как отношение числа таких событий (6) к общему числу событий (27): Р(T = 4) = 6/27. Аналогично Р(T= 5) =12/27, Р(T = 6) =9/27. Тогда zє {4, 5, 6}.

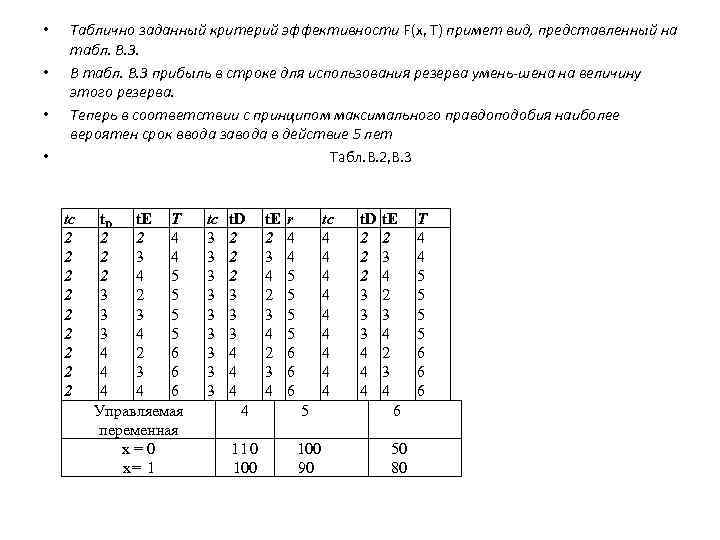• • Таблично заданный критерий эффективности F(x, Т) примет вид, представленный на табл. В. З. В табл. В. З прибыль в строке для использования резерва умень шена на величину этого резерва. Теперь в соответствии с принципом максимального правдоподобия наиболее вероятен срок ввода завода в действие 5 лет Табл. В. 2, В. 3 tc 2 2 2 2 2 t. D t. E Т 2 2 4 2 3 4 2 4 5 3 2 5 3 3 5 3 4 5 4 2 6 4 3 6 4 4 6 Управляемая переменная х = 0 х= 1 tc 3 3 3 3 3 t. D 2 2 2 3 3 3 4 4 110 100 t. E 2 3 4 r 4 4 5 5 6 6 6 tc 4 4 4 4 4 5 100 90 t. D 2 2 2 3 3 3 4 4 4 t. E 2 3 4 6 50 80 T 4 4 5 5 6 6 6

• • • F(0, 5) = 100, что больше, чем F(l, 5) = 90, использовать резерв не целесообразно. Средняя прибыль в соответствии с принципом Байеса для х = О составит MF(x, T) = 6/27*110+12/27*100+9/27*. 50 = 2310/27. Средняя прибыль для х = 1 составит MF(X, Т) = 6/27*100+12/27 * 90+9/27* 80 =2400/27 следовательно, в этом случае использовать резерв целесообразно. Гарантированная оценка ввод завода в строй за максимальный срок 6 лет. В этом случае использовать резерв также целесообразно. Глава 1 ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Термин «линейное программирование» связывается с исследованием и решением следующей задачи Дана система т линейно независимых уравнений с n неизвестными х1, . . хn, называемая системой ограничений задачи линейного программирования: (1 1) Характерной особенностью данной задачи является то, что число уравнений меньше числа неизвестных, т. е. m<п: Требуется найти неотрицательные значения переменных хi>0, (i=1, . . . , n), которые удовлетворяют уравнениям (1 1) и обращают в минимум целевую функцию (1 2) часто называемую линейной формой.

• • Сделаем несколько пояснений по поводу этой задачи. Система уравнений (1 1) для случая, когда число уравнений равно числу неизвестных (т = п) рассматривается в обычной алгебре. Если при этом определитель системы не равен нулю, то система имеет одно единственное решение, для нахождения которого имеются хорошо разработанные приемы. Если же число уравнений меньше числа неизвестных (т<п), то система уравнений (1 1) имеет бесчисленное множество решений, т. е. имеется бесчисленное множество наборов переменных xi (i = 1, . . . , п), которые удовлетворяют уравнениям (1 1). Каждый набор переменных xi (i=1, …, п), удовлетворяющий системе уравнений (1 1), будем называть решением. Однако на переменные хi наложено добавочное ограничение, состоящее в том, что эти переменные должны быть неотрицательны (х>0). В общем случае имеется бесчисленное множество решений, удовлетворяющих этому добавочному условию. Любое решение системы (1 1) с неотрицательными значениями переменных будем называть допустимым решением. Таким образом, суть задачи линейного программирования состоит в том, чтобы из множества допустимых решений выбрать одно, а именно такое, которое обращает в минимум линейную форму (1 2).

• • • • Иногда в задаче линейного программирования все или некоторые из уравнений вида (1 1) имеют вид неравенств. Так, вместо уравнения (1 3) используют неравенство (1 4) или (1 5) Однако такие неравенства легко превратить в урав нения, вводя добавочную переменную n+j≥ 0 так, x чтобы в зависимости от знака неравенства имело место одно из двух выражений (1 6) Такое изменение приводит просто к увеличению числа переменных, что не меняет существа задачи. Иногда стоит задача не минимизации линейной формы (1 2), а максимизации ее. Эта задача сводится к предыдущей путем перемены знака у выражения для q. Поскольку в дальнейшем будут встречаться задачи обоих типов, то условимся значение целевой функции обозначать через q, если требуется ее минимизировать, и через q', если она должна быть максимизирована. Прежде чем искать решение уравнений (1 1), удовлетворяющее всем наложенным требованиям (х i ≥ 0, i=1, . . . , n; q= min), попробуем найти какое либо решение уравнений (1 1). Поскольку число переменных n в этой системе больше числа уравнений т, то одно из возможных решений можно найти, если n—т каких либо переменных положить равными нулю. Полученную при этом систему т уравнений с т неизвестными можно решать обычными методами алгебры. Правда, для того чтобы система т уравнений с т неизвестными имела решение, необходимо, чтобы определитель, составленный из коэффициентов при неизвестных, не обращался в нуль. Если это условие не выполняется, то можно приравнять нулю другие n—т переменных. Полученное при этом решение называется базисным решением. Мы можем ввести теперь некоторую терминологию, широко употребляемую в задачах линейного программирования.

• • • Базисом называется любой набор т переменных, таких, что определитель, составленный из коэффициентов при этих переменных не равен нулю. Эти т переменных называются базисными переменными (по отношению к данному базису). Остальные n—т переменных называются небазисными или свободными переменными. В каждой конкретной системе уравнений (1 1) может существовать несколько различных базисов с различными базисными переменными. Если положить все свободные переменные равными нулю и решить полученную систему т уравнений с т неизвестными, то получим базисное решение. Однако среди различных базисных решений будут такие, которые дают отрицательные значения некоторых переменных. Эти базисные решения противоречат условию задачи и являются недопустимыми. Допустимым базисным решением является такое базисное решение, которое одновременно допустимо, т. е. которое дает неотрицательные значения базисных переменных. Допустимые базисные решения являются наиболее простыми из допустимых решений системы (1 1). Однако на решение задачи накладывается добавочное условие: линейная форма (1 2) должна при найденном решении принимать минимальное значение. Решение задачи при этом добавочном условии усложняется, однако понятие допустимого базисного решения играет очень важную роль и при нахождении полного решения задачи.

• • Примеры задач линейного программирования Линейное программирование возникло в связи с рассмотрением вопросов о нахождении наивыгоднейших вариантов при решении различных планово производственных задач. В этих задачах имеются большая свобода изменения различных параметров и ряд ограничивающих условий. Требуется найти такие значения параметров, которые с некоторой точки зрения были бы наилучшими. К таким задачам относятся задачи нахождения наиболее рационального способа использования сырья и материалов, определения наивыгоднейших производственных режимов, повышения эффективности работы транспорта и т. п. Пример 7 -1. Задача об использовании ресурсов. Для осуществления l различных технологических процессов Т 1, . . . , Тl заводу требуется m видов ресурсов S 1 • • • , Sm (сырье, топливо, материалы, инструмент и т. п. ). Запасы ресурсов каждого вида ограничены и равны b 1, . . . , bm. Известен расход ресурсов на единицу продукции по каждому технологическому процессу. Требуется определить, в каком количестве требуется выпускать продукцию каждого вида, чтобы доход от реализации этой продукции был максимальным. Обозначим через аi расход ресурсов вида Si на единицу продукции вида Tj, а через Cj — доход от реализации единицы продукции вида Tj. Все имеющиеся данные представим в виде табл. 1 1, положив для конкретности 1 = 3, m=4.

• Все имеющиеся данные представим в виде табл. 1 1, положив для конкретности 1 = 3, m=4. Виды ресурсов Расход'рес урсов на единицу продукции Запасы ресурсов T 1 S 2 S 3 S 4 Доход от реализации единицы продукции T 2 T 3 а 11 a 12 a 13 a 23 а 21 a 31 a 41 c 1 а 22 a 32 a 42 b 1 b 2 b 3 b 4 а 33 a 43 c 2 c 3 — Обозначим через xj количество единиц выпускаемой продукции вида Tj. Ограничениями в этой задаче являются требования, чтобы расход ресурсов вида Si (i=1, …, m) на выпуск всех видов продукции не превышал имеющихся запасов: (1 7)

Эти ограничения легко превратить в уравнения, введя переменные xl+i≥ 0, означающие неиспользованные ресурсы вида Si. При этом вместо (1 7) получим: (1 8) Величина дохода от реализации выпущенной продукции будет равна (1 9) Оптимальным планом выпуска продукции будет такое неотрицательное решение системы уравнений (1 8), при котором целевая функция (1 9) будет максимальна. Пример 2 2. Задача о распределении выпуска продукции по предприятиям. План отрасли предусматривает за время Т выпуск следующих видов продукции: A 1 в количестве Ni штук; A 2 в количестве N 2 штук; Al в количестве Nl штук. Эти виды продукции могут выпускаться на r однородных предприятиях П 1. . . , П r. Предполагаем, что ни одно предприятие не может одновременно выпускать несколько видов продукции.

Кроме того, задано: aij — количество продукции Ai выпускаемой на предприятии Пj в единицу времени; bij — стоимость единицы продукции вида Ai выпущенной на предприятии П j xij — время работы предприятия П j по выпуску продукции Ai. Требуется найти такие значения хij, при которых стоимость выпускаемой продукции будет минимальной. Ограничения: 1)время работы каждого предприятия не должно превышать T (1 10) 2) количество выпускаемой продукции должно соответствовать номенклатуре (1 11) Целевая функция будет представлять собой общую стоимость выпущенной продукции. Если принять во внимание, что величина aiibijxij представляет собой стоимость части продукции Ai , выпускаемой предприятием П j, то общая стоимость выпускаемой продукции (1 12)

Согласно условиям задачи эта величина должна быть миними зирована при выполнении ограничений (1 10) и (1 11). Пример 1 -3. Транспортная задача В пунктах Р 1. . . , Pl имеется однородный груз в количествах а 1, …, аl. Его необходимо перевезти в пункты Q 1, . . . , Qr в количествах b 1, . . . , br так, чтобы общая стоимость перевозок была минимальна. При этом предполагается, что количество требуемого груза равно имеющимся запасам (1 13) Обозначим через xij количество груза, перевозимого из пункта Qi в пункт Qj, а через сij — стоимость перевозки единицы этого груза. В задаче имеются следующие ограничения: 1) количество груза, отправляемого из пункта Qi на все пункты назначения, должно быть равно имеющимся запасам аi (1 14) 2) количество груза, прибываемое в Qj со всех пунктов отправления, должно равняться потребности bj. (1 15)

Геометрическая интерпретация задачи линейного программирования Графический метод решения задач линейного программирования (ЗЛП) имеет область применения, так как этот метод используется для ЗЛП с двумя переменными, в которой ограничения выражены неравенствами. Графический метод довольно прост и нагляден, он основан на геометрическом представлении допустимых решений и целевой функции задачи. Рассмотрим следующую задачу: Каждое из неравенств в системе ограничений ЗЛП определяет на координатной плоскости( Х 1, 0, Х 2) некоторую полуплоскость, а система неравенств в целом — пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР, многоугольник решений). ОДР всегда представляет собой выпуклую фигуру, т. е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок А В принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством. Алгоритм решения ЗЛП графическим методом. Шаг 1. Строят многоугольник решений (ОДР): а) на плоскости( Х 1, 0, Х 2) строятся прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки равенств, т. е.

б) находят полуплоскости, определяемые каждым из ограничений задачи. Для этого в конкретное неравенство подставляются координаты какой либо точки (например, (0; 0)) и проверяется истинность полученного неравенства. Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку; в противном случае (неравенство ложное) надо заштриховать полуплоскость, не содержащую данной точки. Замечание. Так как x 1 и х2 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси х1 и правее оси х2, т. е. в I квадранте; в) определяют ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделяют ее. При отсутствии ОДР задача не имеет решений. Шаг 2. Строят вектор N = (c 1, c 2), который указывает направление возрастания целевой функции. Шаг 3. Строят линию уровня (опорную линию) целевой функции перпендикулярно вектору N = {с1, с2). Шаг 4. При поиске максимума целевой функции линия уровня передвигается в направлении вектора N = (с1, с2), при поиске минимума целевой функции — против направления вектора N = (c 1, c 2). Последняя по ходу движения вершина ОДР (или сторона многоугольника решений) будет точкой максимума или минимума целевой функции (бесконечное число решений). Если такой точки (точек) не существует, то делается вывод о неограниченности целевой функции на 'множестве решений сверху (при поиске максимума) или снизу (при поиске минимума). Шаг 5. Определяют координаты точки максимума (минимума) целевой функции: Xmax = (x 1 max x 2 max) или Xmin = (x 1 min, x 2 min) и вычисляют значение целевой функции. Для вычисления координат оптимальной точки решают систему уравнений прямых, на которых находится оптимальное решение. Рассмотрим данный алгоритм на конкретном примере.

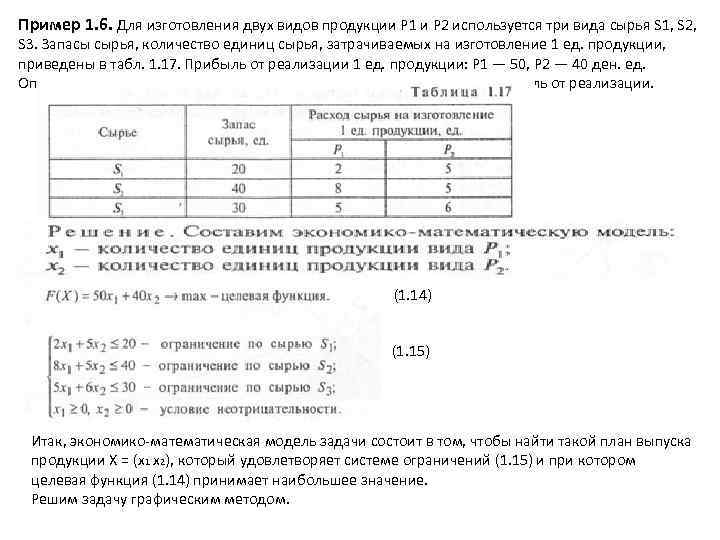Пример 1. 6. Для изготовления двух видов продукции Р 1 и Р 2 используется три вида сырья S 1, S 2, S 3. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление 1 ед. продукции, приведены в табл. 1. 17. Прибыль от реализации 1 ед. продукции: Р 1 — 50, Р 2 — 40 ден. ед. Определить план выпуска продукции Р 1 и P 2, дающий наибольшую прибыль от реализации. (1. 14) (1. 15) Итак, экономико математическая модель задачи состоит в том, чтобы найти такой план выпуска продукции X = (х1 х2), который удовлетворяет системе ограничений (1. 15) и при котором целевая функция (1. 14) принимает наибольшее значение. Решим задачу графическим методом.

Шаг 1. На плоскости (Х 1, 0, Х 2) строим прямые (рис. 1. 1) Шаг 2. Неравенства х1>0, х2>0 означают, что область допустимых решений задачи будет расположена в первой координатной четверти. Шаг 3. Находим полуплоскости, определенные каждым из ограничений задачи. Затем находим их пересечение — это и будет область допустимых решений (ОДР) задачи. 0 ABCD — область допустимых решений задачи (многоугольник решений). Шаг 4. Строим вектор N = (50; 40) или N = (5; 4). Шаг 5. Перпендикулярно вектору N строим линию уровня (опорную линию). Шаг 6. Линию уровня перемещаем вдоль вектора N для нахождения наибольшего значения до самой удаленной точки ОДР. В нашей задаче самая удаленная точка — точка С. Шаг 7. Определяем координаты точки С. Она находится на пересечении (2) и (3) прямых. Записав систему уравнений этих прямых, найдем координаты: В результате получаем оптимальное решение X = (3, 9; 1. 7)Подставляя найденный результат в целевую функцию, на оптимальное значение: Для того чтобы прибыль от реализации продукции была бы наибольшей и составляла 265, 1 ден. ед. , необходимо выпускать продукцию вида Р 1 в количестве 3, 9 ед. , продукцию вида Р 2 1, 7 ед

В зависимости от вида области ограничений и типа целевой функции возможны различные ситуации. Очевидно, что решение будет отсутствовать в случае несовместности ограничений, когда область допустимых решений является пустым множеством (рис. а). Кроме того, оптимальное решение может отсутствовать в том случае, когда область допустимых решений задана бесконечной полуплоскостью. Если она не ограничена сверху, то для нее невозможно отыскать максимум, а если снизу — минимум(рис. б) б неограниченна сверху и снизу в На рис. в)опорная прямая проходит через сторону АВ многоугольника решений и, следовательно, в любой точке отрезка AВ существует решение, которое формально можно считать оптимальным. Однако на отрезке АВ может быть найдена единственная точка, которая обеспечить максимальное значение целевой функции

• • • 1 2. РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ а) Алгебра симплекс метода Существо симплекс метода состоит в следующем. Прежде всего находится какое либо допустимое базисное решение. Его можно найти, приняв какие либо n—m переменных за свободные, приравняв их нулю и решив получившуюся систему уравнений (1 1). Если при этом некоторые из базисных переменных окажутся отрицательными, то нужно выбрать другие свободные переменные, т. е. перейти к новому базису. После того, как найдено допустимое базисное решение, проверяется, не достигнут ли уже максимум целевой функции q’. Если нет, то ищут новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение целевой функции q’. Затем процедура повторяется. Поскольку в качестве нового допустимого базисного ре шения выбирается лишь такое, которое увеличивает значение целевой функции, данный метод дает возможность рассматривать минимум допустимых базисных решений и довольно быстро приводит к цели. Разберем этот метод более подробно на рассмотренном ранее примере. Обратимся к системе уравнений (1 20), для которой требуется найти неотрицательное решение, обращающее в максимум целевую функцию (1 19). Поскольку n—m = 2, то в качестве свободных можно взять любые две переменные, например x 1 и х2. Положив их равными нулю, из (1 20) находим базисное решение x 1 = x 2 = 0, xз = 2, x 4 = 2, x 5=5, которое является допустимым и при котором q’=x 1—х2=0.

• • Проверку того, не достигнут ли при найденном решении максимум целевой функции, можно сделать путем поиска нового базисного решения, при котором целевая функция будет больше. Для перехода к новому допустимому базисному решению одну из свободных переменных x 1 или х2 следует сделать базисной. При этом она будет отличной от нуля, т. е. возрастет. Следовательно, если какая либо из свободных переменных входит в выражение для целевой функции со знаком « + » , а значит при ее увеличении целевая функция увеличивается, то максимум целевой функции не достигнут и данную переменную следует превратить в базисную, сделав ее отличной от нуля. Однако при возрастании свободной переменной некоторые из базисных переменных начнут уменьшаться. Так как отрицательные значения переменных недопустимы, в качестве новой свободной переменной следует взять ту из базисных, которая раньше других обратится при этом в нуль,

• В рассматриваемом примере в выражение для целевой функции (1 22) со знаком « + » входит свободная переменная х1. Значит, максимум целевой функции не достигнут и переменную x 1 следует сделать базисной. Для определения новой свободной переменной выразим базисные переменные х3, x 4 х5 через свободные, приведя уравнения (1 20) к виду (1 23). Из этих уравнений, видим, что при х2 = 0 увеличение х1 не приводит к уменьшению х3, но уменьшает x 4 и х5, при этом x 4 уменьшается быстрее чем х5 , так что при x 1 = 2 получаем x 4=0, x 5 = 3>0. Таким образом, переменную х4 следует сделать свободной переменной, что приводит нас к новому базису x 4 х3, х5. • (1 (1 23) • Для продолжения решения разрешим систему исходную систему относительно новых базисных переменных, приведя ее к виду • Целевую функцию также выразим через новые свободные переменные х2 и х4;

Повторяя проведенные ранее рассуждения, приходим к выводу, что максимум целевой функции не достигнут и следует свободную переменную х2 перевести в базисную, а базисную переменную х5 — в свободную. Новый базис образуют при этом переменные x 1 х2, х3. Разрешая исходные уравнения (1 17) относительно новых базисных переменных, получаем: (1 24) Целевая функция при этом принимает вид: (1 25) Рассмотренный метод решения задачи линейного программирования обладает тем недостатком, что связан с громоздкими преобразованиями системы линейных уравнений из одной формы в другую. Значительного упрощения преобразований можно добиться, если представлять уравнения в виде таблиц, содержащих коэффи циенты при переменных. Переход от одной системы уравнений к другой при этом сводится к пересчету коэффициентов в таблицах, что осуществляется по чисто формальным правилам, хорошо приспособленным к тому же, для компьютерного решения.

Табличный метод нахождения оптимального решения При пользовании табличным методом удобно ввести специальную форму записи для уравнений (1 1) и целевой функции (1 2). Обозначим через xi’, i=1, . . . , т базисные переменные, а через x"j, j=1, (n—т) — свободные переменные. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу линейного программирования в следующем виде: Максимизировать (1 26) при условиях (1 27) При такой форме записи задача может быть представлена следующей матрицей коэффициентов при переменных: (1 28) По виду коэффициентов матрицы (1 28) легко судить, является ли найденное базисное решение допустимым и, если оно допустимо, то будет ли оптимальным. Действительно, замечая, что столбец коэффициентов ai 0, i≠ 0 представляет собой базисное решение, соответствующее базису х'и. . . , х'т, , а строка коэффициентов α 0 j, j≠ 0 представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении для q’, приходим к выводу, что базисное решение, соответствующее базису х’ 1, . . . , х'т допустимо, если αi 0≥ 0, i≠ 0.

Если, кроме того, α 0 j>0, j≠ 0, то это базисное решение является и оптимальным. Очевидно также, что при оптимальном базисном решении коэффициент α 00 дает значение q' = q’макс = —qmin. Начнем решение задачи с нахождения какого либо допустимого базисного решения, которое в общем случае не является оптимальным, Это базисное решение представим таблицей коэффициентов, составленной по типу матрицы (1 28). Для перехода к лучшему базисному решению необходимо преобразовать матрицу коэффициентов. Способ такого преобразования сформулируем в виде системы правил, которые проиллюстрируем на примере задачи, решенной в предыдущем параграфе. Мы не будем давать строгое обоснование этим правилам. Отметим только, что они в точности соответствуют тем преобразованиям системы уравнений, которые осуществлялись в предыдущем примере и могут быть легко проверены путем сопоставления соответствующих преобразований. Пусть задача линейного программирования дана в виде уравнений и целевой функции , которую надо максимизировать. Принимая x 1 и х2 за свободные переменные, приведем эту систему уравнений и целевую функцию к следующему виду. ( 1 29)

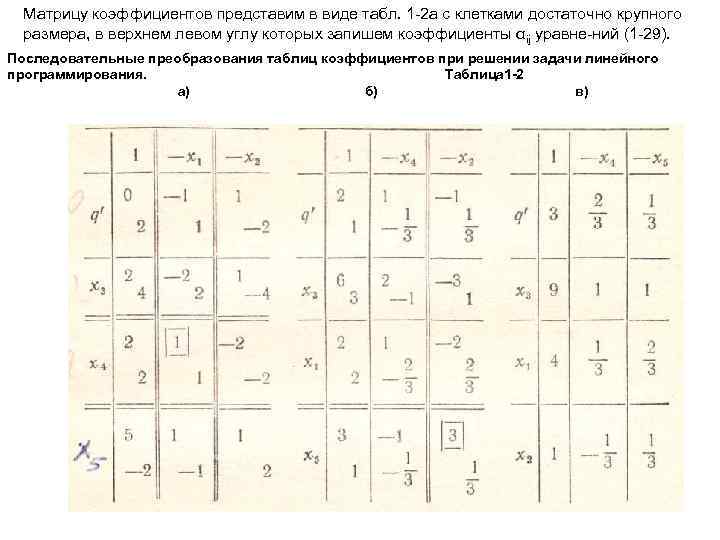Матрицу коэффициентов представим в виде табл. 1 2 а с клетками достаточно крупного размера, в верхнем левом углу которых запишем коэффициенты αij уравне ний (1 29). Последовательные преобразования таблиц коэффициентов при решении задачи линейного программирования. Таблица 1 -2 а) б) в)

Проверим, не найдено ли уже оптимальное решение, условием которого является α 0 j≥ 0, j≠ 0. Поскольку αo 1 (коэффициент при—x 1 в выражении для q’) отрицателен, то оптимальное решение не найдено и переменную x 1 следует сделать базисной. Выделим столбец, соответствующий переменной х1 сдвоенными линейками. Если отрицательными окажутся коэффициенты a 0 j при нескольких свободных переменных, то в базисную можно переводить любую из них. Определим теперь, какую же из базисных переменных следует сделать свободной. Очевидно ту, которая быстрее обратится в нуль при увеличении х1, Это будет та базис ная переменная xi , для которой коэффициент в отмеченном столбце αi 1>0 и отношение αiо/αi 1 наименьшее. Такой переменной является базисная переменная x 4 с α 4 о = 2 и α 41=l. Строку, соответствующую базисной пе ременнойx 4 также отмечаем двойными линейками. Коэффициент λ = α 41 , стоящий в левом верхнем углу клетки на пересечении отмеченных строки, и столбца, назовем генеральным коэффициентом. В нашем случае λ= 1 (взят в рамку). Теперь следует заполнить нижние углы каждой клетки. Это делаем по следующим правилам: 1)в клетку на пересечении отмеченных строки и столбца записываем 1/λ; 2)в клетках отмеченной строки записываем верхние коэффициенты, умноженные на 1/λ (верхние коэффициенты за исключением генерального коэффициента выделены жирным шрифтом);

3) в клетках отмеченного столбца записываем верхние коэффициенты, умноженные на 1/λ (нижние коэффициенты за исключением клетки с генеральным коэффициентом выделены жирным шрифтом); 4) в остальных клетках записываем произведение выделенных жирным шрифтом коэффициентов, на пересечении которых стоит данная клетка. Затем переходим к заполнению табл. 1 2 б, которая отличается от табл. 1 2 а тем, что отмеченная свободная переменная x 1 стала базисной, а отмеченная базисная переменная , x 4. стала свободной, Верхние левые углы клеток табл. 71 2 б заполняются по следующим правилам: 1) строка и столбец, соответствующие новым свободной и базисной переменным, заполняются нижними коэф фициентами отмеченных строки и столбца табл. 1 2 а; 2) в остальные клетки записываются суммы коэффициентов, стоящих в соответствующих клетках табл. 1 2 а. Заполненная таким образом табл. 1 2 б соответствует матрице коэффициентов при новом базисе x 1 xз, х5. Далее вся процедура повторяется. Поскольку в табл. 1 2 б. коэффициент α 02<0, то оптимальное решение не найдено. Следовательно, нужно согласно приведенным правилам заполнить нижние левые углы табл. 1 2 б и перейти к новой табл. 1 2 в, соответствующей базису x 1 х2, х3. В этой таблице коэффициенты aoj, j≠ 0 положительны, и она дает оптимальное решение задачи, которое находим по столбцу свободных членов:

ВЗАИМНО ДВОЙСТВЕННЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В различных разделах математики встречаются так называемые теоремы двойственности. Каждая из них позволяет из любого утверждения данной теории построить по определенному стандартному правилу—другое утверждение таким образом, что из справедливости первого автоматически следует справедливость второго. замечательный пример теоремы двойственности мы встречаем и в линейном программировании. Помимо того, что эта теорема удваивает число решенных задач, она имеет также и важные принципиальные следствия. Начнем с описания взаимно двойственных задач. Пусть дана некоторая задача линейного программирования, которую мы будем в дальнейшем называть исходной задачей или задачей 1. При этом ограничения заданы в форме неравенств; нам известно, что любая задача может быть приведена к такому виду. Итак, дана система (1 -30) т линейных неравенств с n неизвестными и линейная форма (1 31) Требуется из всех неотрицательных решений системы (1 30) выбрать такое, которое минимизирует форму (1 31)

С данной задачей мы сейчас свяжем другую задачу, которую назовем двойственной по отношению к исходной или задачей 1’. Вот ее формулировка: дана система (1 32) n линейных неравенств с m неизвестными и линейная форма (1 33) Требуется из всех неотрицательных решений системы (1 32) выбрать такое, которое максимизирует форму (1 33). Сравнивая обе задачи, мы замечаем, что: 1. Матрица из коэффициентов при неизвестных в исходной задаче и аналогичная матрица в двойственной задаче получаются друг из друга „транспонированием" (т. е. заменой строк столбцами, с сохранением их порядка). 2. В правых частях системы ограничений каждой задачи стоят коэффициенты формы, взятой из другой задачи. 3. В системе ограничений исходной задачи все неравенства типа ≥, причем в этой задаче требуется достичь минимума формы f. В системе ограничений двойственной задачи все неравенства типа ≤ причем в этой задаче необходимо достичь максимума формы φ.

Представим теперь, что за исходную принимается не первая, а вторая задача. Разумеется, для этого необходимо сделать так, чтобы все неравенства этой задачи стали неравенствами типа ≥, что достигается умножением обеих, частей каждого неравенства на — 1; далее, задачу разыскания максимума φ следует заменить эквивалентной задачей разыскания минимума — φ (очевидно, maxφ= —min( —φ)). Тогда, как нетрудно понять, двойственная задача будет совпадать с первой из рассмотреныx, хотя и окажется записанной по другому: вместо неравенств (1 31)будут фигурировать неравенства, полученные из них умножением на — 1 (с изменением знаков неравенств на противоположные), а вместо минимума f будет разыскиваться максимум — f. Таким образом, двойственная задача для второй совпадает с первой, и тем самым отношение двойственности оказывается взаимным. Поэтому две указанные выше задачи называют взаимно двойственными. Теорема двойственности. Если исходная задача имеет решение, то и двойственная ей также имеет решение. При этом минимум формы f равен максимуму формы φ: min f= maxφ. Если в исходной задаче линейная форма не ограничена снизу, то в двойственной задаче система ограничений не имеет ни одного неотрицательного решения. По поводу последнего утверждения теоремы сразу же заметим, что оно не допускает обращения. Иными словами, если в одной из задач система ограничений противоречива (в области неотрицательных значений неизвестных), то отсюда вовсе не следует, что в двойственной задаче линейная форма не ограничена; может оказаться, что и в ней система ограничений также противоречива,

Понятие о целочисленном программировании Во многих задачах линейного программирования переменные являются неделимыми на части величинами. Так, предприятие не может выпустить 7, 5 самолета, 4, 8 турбины и т. п. В таких задачах к условиям (1 1) и (1 2) добавляется требование, чтобы переменные xi выражались целыми числами или бы элементами конечного множества. Геометрически это означает, что допустимыми решениями будет не вся область допустимых решений, определяемая ограничениями (1 1), а лишь отдельные дискретные точки этой области, как показано на рис. 1 3. Рис. 1 3. Множество допустимых решений в задаче целочисленного программирования. Можно, конечно, попытаться решить подобную задачу, не считаясь с условием целочисленности, и найти решение, определяемое на рис. 1 3 точкой 1, а затем округлить это решение до ближайших целых чисел, получив, таким образом, в качестве целочисленного решения точку 2. Однако при этом может получиться решение, далекое от оптимального. Так, на рис. 1 3 оптимальным целочисленным решением будет служить точка 3.

• • • Существует ряд методов решения задачи целочисленного программирования, из которых наиболее распространенным является метод Гомори. Не останавливаясь на вычислительной стороне метода Гомори укажем лишь общую идею этого метода. Метод Гомори основан на применении симплекс метода, с помощью которого ищется оптимальное решение, не учитывающее целочисленности или дискретности переменных. Если это решение оказалось нецелочисленным, то вводится добавочное ограничение, геометрически предcтавляющее собой линию ab на рис. 3, которая отсекает часть области допустимых решений вместе с полученным оптимальным решением, не содержащую ни одной целочисленной допустимой точки. При этом добавочном ограничении найденное оптимальное решение окажется вне новой области допустимых решений, т. е. будет недопустимым. Поэтому задача решается снова симплекс методом и находится оптимальное решение уже для новой области допустимых решений. Если это новое решение опять не является целочисленным, то процедура повторяется. За последнее время для решения задачи целочислен ного программирования успешно применяются комбина торные методы, среди которых важнейшим является метод ветвей и границ.

• • Транспортная задача Есть п пунктов отправления, в которых имеются запасы произведенной продукции в количествах ai i= 1, …, n, есть т пунктов назначения с заявками на произведенную продукцию в количествах bj Если ∑ ai= ∑b j то имеем задачу с правильным балансом. При невыполнении этого условия вводим дополнительный фиктивный пункт отправления или назначения, емкость которого равна поло жительной разности между этими суммами. Стоимость доставки единицы грузов из i го пункта отправления в j й пункт назначения составляет величину сij причем затраты, связанные с фиктивными пунктами, должны быть нулевыми. Тогда минимальные затраты на выполнение плана перевозок определятся минимизацией суммарных затрат на перевозки • (1. 34) •

• при условиях: (1. 35) В (1. 20) п первых условий предусматривают, что все грузы из всех пунктов отправления должны быть вывезены, а последние т условий что все заявки во всех пунктах назначения должны быть выполнены. Матрица ограничений в транспортной задаче состоит только из нулей и единиц. Это обстоятельство позволяет модифицировать симплекс метод к более экономному алгоритму решения, получившему название метод потенциалов. Суть этого метода рассмотрим на простых примерах. Пусть есть три пункта отправления ai = (10, 20, 30) и три пункта назначения bj = (12, 17, 31), причем с матрицей затрат

• Представим исходные данные в виде табл. 1. 1. Исходные данные к транспортной задаче В первом столбце этой таблицы отражены запасы в пунктах отправления, в первой строке потребности пунктов назначения, остальные клетки таблицы содержат путь из пункта i в пункт j, стоимость транспортировки задана в правом верхнем углу каждой клетки. Первый этап решения состоит в генерации допустимого решения. Число неизвестных тп = 3 • 3 = 9, число условий в ограничениях т + п— 1 =3 + 3 — 1 = 5. В соответствии с теоремой 2 число небазисных переменных, т. е. переменных, заведомо равных нулю, составляет 4. Допустимое решение наиболее часто генерируют, максимально загружая в первую очередь наиболее дешевые пути.

• • • Стоимость сij = 2 минимальна. Перевезем по этому пути самое большое количество груза min(ai, bj) = min(10, 12) = 10 единиц. Заявку первого пункта мы удовлетворили не полностью, осталось еще 2 единицы. Следующее минимальное значение в матрице сij = 3, но из первого пункта мы уже все вывезли, поэтому перевезем из пункта аз в пункт b 2 17 единиц со стоимостью сij = 3, тем самым удовлетворяя заявку второго пункта. Последовательно определяя все базисные переменные, получим допустимое решение, претендующее на оптимальность (табл. 1. 2). Таблица 1. 2 В этом решении все грузы вывезены и все заявки выполнены, однако решение получено попыткой минимизировать каждое слагаемое в критерии, что не может гарантировать минимальную величину всей суммы. Для проверки оптимальности используется метод потенциалов, позволяющий определит возможность улучшения решения. Для этого определяются числа (потенциалы) αi и βj из условия αi + βj = сij для хij > 0. Таких чисел т + п = 6, а базисных переменных на единицу меньше, поэтому значение одного из потенциалов выбирают произвольно. Пусть α 1= 0, тогда α 1+β 1 = с11, отсюда β 1= 2. Последовательно используя условие, в котором один из потенциалов уже определен, получим табл. 1. 3.

Таблица 1. 3 Потенциалы псевдостоимости Таблица 1. 4 Проверка оптимальности для задачи с правильным балансом Далее вычисляются псевдостоимости с'ij = αi + βj для хij = 0. Псевдостоимости отражены в левом углу каждой пустой клетки. Если выполняется условие с'ij < сij, решение оптимально. Так как это условие выполнено, план перевозок, отраженный в табл. 1. 4, оптимален. В этом алгоритме предполагается, что все базисные переменные отличны от нуля. Однако в процессе расчетов может оказаться, что некоторые переменные в базисе нулевые. В этом случае имеем дело с вырожденным решением.

Пример 1. 20. По данным о запасах груза на трех складах, потребностях в грузе у четырех магазинов и тарифах на перевозки, приведенных в табл. 1. 5, определить оптимальный план перевозок груза с наименьшей стоимостью. Таблица 1. 5

Решение. Обозначим через Xij количество груза, перевозимого из пункта i в пункт j, где Балансовое равенство выполняется (суммарная потребность в грузе равняется суммарным запасам: 3 + 6 + 7 + 5 = 7 + 8 + 6), значит, транспортная задача – с правильным балансом (закрытая). Тогда экономико математическая модель задачи выглядит следующим образом:

Построим первоначальный опорный план методом наименьшего тарифа. На первом шаге заполняется клетка с наименьшим тарифом 1. Заметим, что клеток с наименьшим тарифом две, но, так как максимальные объемы поставок в обе клетки одинаковы, заполнение таблицы можно начать как с той, так и с другой клетки. Будем осуществлять перевозку с первого склада ко второму потребителю: Тем самым на первом складе осталась 1 ед. груза, а потреб ности второго магазина удовлетворены полностью. Поэтому далее выбираем клетку с наименьшим тарифом из второго, чет вертого и пятого столбцов таблицы. Это клетка с тарифом 2: Далее заполнение таблицы происходит следующим образом:

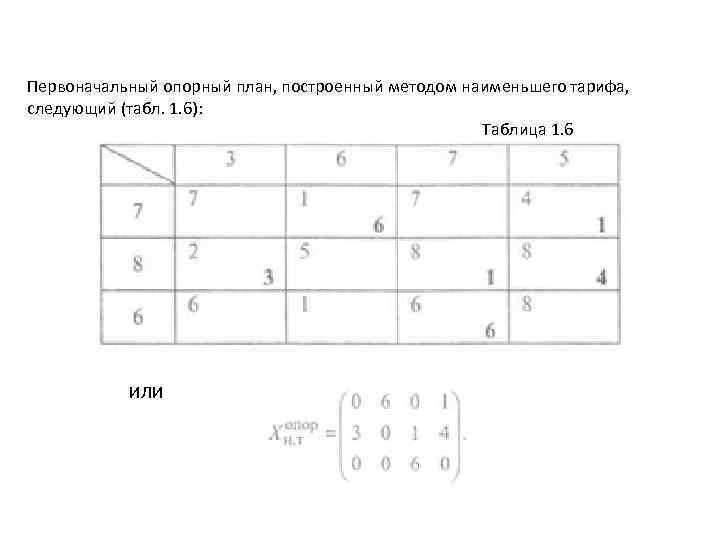Первоначальный опорный план, построенный методом наименьшего тарифа, следующий (табл. 1. 6): Таблица 1. 6 ИЛИ

Проверим найденный опорный план на вырожденностъ. Вычислим m + n— 1: m + n— 1 = 3 + 4— 1 =6, т. е. число занятых клеток равно 6. Так как эти значения совпадают, то найденный опорный план является невырожденным. Стоимость перевозки: Fmin = 92 ден. ед. Практически всегда метод наименьшего тарифа дает более приближенный к оптимальному опорный план, чем метод северо западного угла. Проверим план, построенный методом наи¬меньшего тарифа, на оптимальность. Для этого по занятым объемами перевозок клеткам составим систему уравнений для расчета потенциалов :

Неизвестные потенциалы u 1 и 2, u 3, v 1 , v 2, v 3, v 4, находим из этой системы уравнений, полагая u 1=0. Тогда из первого и второго уравнений: v 2=l, v 4=4; далее из предпоследнего: u 2=4; затем из третьего и четвертого уравнений: v 1= — 1, v 3=4; и, наконец, из последнего: u 3=2. Перепишем матрицу перевозок, добавив справа столбец с потенциалами а внизу — строку с потенциалами V. (табл. 1. 7). Таблица 1. 7 3 6 7 7 1 6 8 5 6 Ui 0 7 4 1 2 3 6 5 8 4 8 1 4 1 8 2 6 Vj 1 1 6 4 4

Посчитаем оценки свободных клеток по формуле Δij=ui+vj+Сij : Δ=ui+vj cij>0 Таблица 1. 8

Контур может иметь только повороты на 900 и содержать только одну вершину, соответствующую свободной переменной. Все остальные вершины должны соответствовать базисным переменным. Число вершин обязательно должно быть четным. С вершинами связаны чередующиеся знаки «+» или « » . Первый знак «+» ставится у вершины, соответствующей свободной переменной. Величину, на которую надо перераспределить поставки для улучшения плана перевозок, определяем по формуле d=min{xij” “} по значениям i и j, соответствующим базисным вершинам, имеющим знак « » в цикле. В нашем случае d=4. В клетках цикла, помеченных знаком «+» объем перевозок увеличивается на эту величину, знаком « » уменьшается. 7 8 6 3 7 6 7 5 4 1 7 1 « 5» 6 « 2» 5 8 2 8 4 « 0» 3 1 « 5» 6 1 8 6 « 4» 6 « 2» 3 6 7 5 7 0 2 0 5 8 3 0 5 0 6 0 4 2 0

или Проверим план, построенный методом наименьшего тарифа, на оптимальность.

Решив систему, получаем новые значения для потенциалов uj, vj, которые заносим в таблицу перевозок. Проверяя план на оптимальность, замечаем, что все оценки свободных клеток не положительны, т. е. полученный план перевозок является оптимальным Стоимость перевозки = 84 ден. ед. Замечание. Если среди оценок свободных клеток нет нулевых оценок, то найденный оптимальный план является единственным. Если же среди оценок свободных клеток есть нулевая оценка: Δ 14=0, то задача имеет множество оптимальных планов (множество решений). Для клетки с нулевой оценкой можно построить цикл и перераспределить груз. В результате полученный оптимальный план будет иметь то же значение целевой функции.

Транспортная задача с неправильным балансом. ( открытая транспортная задача) Такую транспортную задачу можно преобразовать в задачу с правильным балансом путем введения фиктивного пункта производства или потребления. В случае если суммарный запас груза превышает суммарные потребности на S ед. , добавляется фиктивный потребитель с потребностью, равной S ед. Если же суммарные по требности превышают суммарный запас груза, то добавляют фиктивного поставщика. Тарифы перевозок в строке (столбце! фиктивного поставщика (потребителя) полагают равными 0. Пример. Для задачи оптимального планирования перевозок груза тарифы перевозок, запасы груза и потребности в грузе такие же, как в предыдущем примере, за исключением потребности третьего магазина, которая составляет 9 ед. Найти оптимальный план перевозок. Решение. Балансное равенство не выполняется, поэтому задача с неправильным балансом, так как суммарная потребность в грузе превышает суммарный запас на 2 ед. Для решения этой задачи вводим фиктивного поставщика с запасом груза 2 ед. (табл. 1. 10).

Таблица. 1. 10 Модель задачи запишется следующим образом: хij количество груза, перевозимого с i склада в j магазин,

Построение первоначального опорного плана, проверка плана на оптимальность и переход в случае неоптимального плана к новому для открытой транспортной задачи осуществляются точно так же, как и для закрытой. Решая закрытую задачу, находим ее оптимальный план

Чтобы получить оптимальный план исходной задачи, нужно отбросить последнюю строку, соответствующую фиктивному поставщику: Отброшенная строка плана х* означает, сколько единиц груза i недополучат потребители, а именно третий магазин недополучит 2 ед. груза.

• • • Резюме Многие экономические задачи формулируются в терминах линейного программирования, поскольку функции прибыли, стоимости, затрат суть линейные функции переменных, связанных с объемами выпуска, продаж и других подобных факторов. Градиент функции (вектор цен) не может быть нулевым, что вынуждает искать решение на границе области допустимых решений. Используемый с этой целью симплекс метод позволяет перебирать крайние точки множества допустимых решений с монотонно улучшаемым значением критерия оптимальности. Программная реализация симплекс метода имеется в большинстве пакетов прикладных программ.

• • ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ Задача динамического программирования (ДП) формулируется следующим образом: найти минимум (максимум) функции • (2. 1) • (2. 2) Эта задача имеет следующую геометрическую интерпретацию. Введем семейство прямых, каждая из которых соответствует переменной х, (рис. 2. 1). Теперь задача минимизации аддитивной функции свелась к поиску ломаной кратчайшей длины, соединяющей прямые x 0 и х1. Каждая дуга этой ломаной, соединяющей некоторые точки Рис. 2. 1. Геометрическая интерпретация задачи динамического программирования представляет собой одно из слагаемых в сумме (2. 1).

• • Идея метода динамического программирования и более общего метода последовательного анализа вариантов состоит в возможности минимизировать не всю сумму (2. 2) по всем переменным, а только пару слагаемых из нее по одной переменной. Цена за эту возможность необходимость ее решения n+1 раз. Другая интерпретация метода динамического программирования состоит в возможности находить оптимальные решения в задачах минимизации функционалов вида встречающихся в теории оптимального управления. Для них Р. Беллманом и был разработан метод динамического программирования. В дискретном варианте интервал интегрирования разбивается на N шагов с достаточно малым интервалом h = T/N, дискретным временем ti = ih, i = 0, … N— 1, и величина интеграла может быть представлена формулой трапеций в виде что представляет собой аддитивную функцию от переменных ui

• • Методы динамического программирования основаны на возможности представления процесса принятия управляющих решений в виде цепочки последовательных действий или шагов, что позволяет находить оптимальное решение путем разложения исходной задачи на несколько небольших и менее сложных задач. Алгоритм пошаговой оптимизации опирается на сформулированный Р. Беллманом принцип оптимальности: неважно, каким было первоначальное состояние системы и какие ранее применялись управления; на текущем шаге нужно выбрать такое управление, чтобы оно в совокупности с оптимальными управлениями на последующих шагах приводило к наилучшему результату. С помощью методов динамического программирования решаются задачи календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию, распределения инвестиций между возможными на правлениями их использования, составления календарных пла нов ремонта или замены оборудования, поиска кратчайших рас стояний на транспортной сети, разработки правил управления спросом или запасами и др.

• Каждая задача имеет свои особенности и требует разработки собственного подхода к ее решению. Приведем общую постановку задачи динамического программирования. Рассматривается некая система S, которая под воздействием управления переводится из состояния S 0 в состояние Sn. Предполагается, что управление можно разбить на п шагов, тогда переход из состояния S 0 в состояние Sn можно представить в виде графа (рис. 4. 1), где Хк— управление на к ом шаге (k=1, 2, . . . , и), Sk — состояние системы после к то шага управления. В общем виде задачу динамического программирования можно сформулировать следующим образом: необходимо определить такое управление X* = (X*1 Х*2, . . . , Х*п), переводящее систему из состояния S 0 в состояние Sn, при котором целевая функция Z=F(S 0, X*) принимает максимальное (минимальное) значение. Особенности модели задачи динамического программирования следующие: 1) задача оптимизации формулируется как конечный многошаговый процесс управления; 2) выбор управления Хк на каждом шаге зависит только от состояния системы, сложившегося к этому шагу Sk 1; 3) состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk 1 и управляющего воздействия на к ом шаге Хк и может быть записано в виде уравнения состояния системы:

4)целевая функция является аддитивной от показателей эффективности каждого шага. Обозначим показатель эффективности к го шага через Zk =φ(Sk 1, , Хк), тогда Рассмотрим алгоритм решения задач динамического программирования. Шаг 1. Выбираем способ деления процесса управления на шаги. Шаг 2. Выбираем параметры, характеризующие состояние системы Sk, и переменные управления Хк на каждом шаге. Шаг 3. Составляем уравнения состояний. Шаг 4. Вводим целевые функции для каждого шага Zk и суммарную целевую функцию Z. Шаг 5. Записываем уравнение Беллмана для Zn и Zk , к = n l, n 2, . . . , 2, 1.

Шаг 6. При движении от шага п к шагу 1 (условная оптимизация), делая предположения о возможных вариантах значений переменных, характеризующих состояние системы, и возможных вариантах управления, решаем предварительно уравнения Беллмана и получаем две последовательности функций{Z* k} и {X*k} Шаг 7. При движении от шага 1 к шагу n (безусловная оптимизация), используя результаты условной оптимизации, получаем оптимальное решение для конкретного начального состояния S 0: 4. 2. Задача об оптимальном распределении инвестиций Требуется распределить имеющиеся С ден. ед. среди n предприятий таким образом, чтобы после освоения инвестиций суммарная прибыль всех предприятий была максимальной. Прибыль предприятий в зависимости от количества вложенных в них средств х(. определяется функциями φк, к = 1, … , n, представленными в табл. 4. 1.

Таблица 4. 1 Математическая модель задачи выглядит следующим образом: Представим эту задачу как задачу динамического программирования

В качестве системы S здесь выступает п предприятий. Состояние системы определяется количеством денежных средств, выделенных каждому предприятию — хк*. Управление системой заключается в распределении инвестиций в объеме С ден. ед. среди n предприятий. Разобьем процесс распределения инвестиций на несколько шагов. Шаг 1. Выделяем инвестиции только одному предприятию (например, последнему или первому — последовательность не имеет значения). Шаг 2. Выделяем инвестиции двум предприятиям (например, последнему и предпоследнему, первому и второму), и т. д. ………………………………. Шаг n. Выделяем инвестиции всем n предприятиям. Составим уравнение Беллмана для вычисления суммарной прибыли на каждом шаге: где Сn — возможный объем инвестиций, который может быть выделен на шаге n (т. е. n му предприятию); где Ск — возможный объем инвестиций, который может быть выделен на к м шаге (т. е. n му, (n 1) му, . . . , (n к+1) му предприятиям);

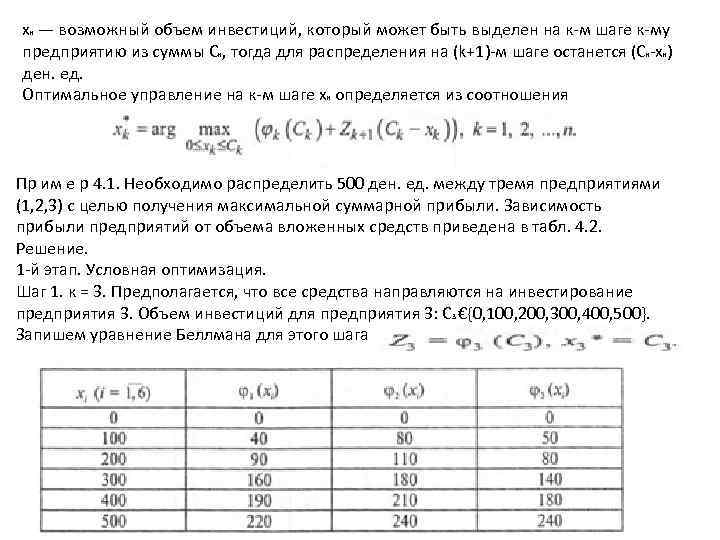хк — возможный объем инвестиций, который может быть выделен на к м шаге к му предприятию из суммы Ск, тогда для распределения на (k+1) м шаге останется (Ск хк) ден. ед. Оптимальное управление на к м шаге хк определяется из соотношения Пр им е р 4. 1. Необходимо распределить 500 ден. ед. между тремя предприятиями (1, 2, 3) с целью получения максимальной суммарной прибыли. Зависимость прибыли предприятий от объема вложенных средств приведена в табл. 4. 2. Решение. 1 й этап. Условная оптимизация. Шаг 1. к = 3. Предполагается, что все средства направляются на инвестирование предприятия 3. Объем инвестиций для предприятия 3: С 3 €{0, 100, 200, 300, 400, 500}. Запишем уравнение Беллмана для этого шага:

Результаты расчетов на данном шаге представлены в табл. 4. 3. Шаг 2. к = 2. Предполагается, что все средства направляются на инвестирование предприятий 2 и 3. Объем инвестиций для двух предприятий может составить: С 2 € {0, 100, 200, 300, 400, 500}; при этом предприятию 2 из этой суммы можно выделить любое количество х2 ≤ С 2. Запишем уравнение Беллмана для шага 2:

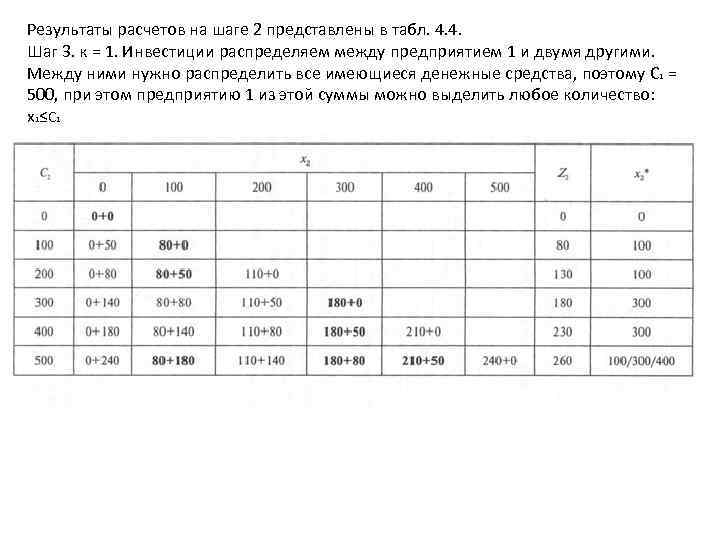Результаты расчетов на шаге 2 представлены в табл. 4. 4. Шаг 3. к = 1. Инвестиции распределяем между предприятием 1 и двумя другими. Между ними нужно распределить все имеющиеся денежные средства, поэтому С 1 = 500, при этом предприятию 1 из этой суммы можно выделить любое количество: x 1≤С 1

Уравнение Беллмана для шага 3 запишется следующим образом: Результаты расчетов на шаге 3 представлены в табл. 4. 5.

2 й этап. Безусловная оптимизация. Шаг 1. По данным табл. 4. 5 максимальная прибыль при распределении 500 ден. ед. между тремя предприятиями составит Z 1=290 ден. ед. , при этом предприятию 1 нужно выделить x 1*= 300 ден. ед. Ш а г 2. Определим величину оставшихся денежных средств, приходящихся на долю предприятий 2 и 3: С 2 = С, Х 1* = 500 300 = 200 ден. ед. По данным табл. 4. 4 находим, что при С 2 = 200 Z 2 = 130, х2* = 100. Это означает, что предприятию 2 следует выделить 100 ден. ед. , максимальная прибыль предприятия 1 составит: Z Z 2 = 290 130 = 160 = φ1(300) ден. ед. Шаг 3. Определим величину оставшихся денежных средств, приходящихся на долю предприятия 3: С 3 = С 2 – х2* = 200 100 = 100 ден. ед. При этом максимальная прибыль предприятия 2 составит: Z 2 Z 3= 130 50 = 80 = φ2( 100) ден. ед. , а предприятия 3 соответственно: Z 3 = 50 = φ3(100) ден. ед. Таким образом, оптимальная стратегия распределения инвестиций: х* = (300, 100) дает возможность получить максимальную суммарную прибыль: Z* = φ1(300) + φ2 (100) + φ 3 (100) = 160 + 80 + 50 = 290 ден. ед.

• Динамическое программирование является эффективным способом решения задач оптимального управления. В непрерывном случае оно используется сравнительно редко ввиду сложности решения уравнения Беллмана в частных производных, осложненных опе рацией максимизации. Применительно к дискретным многошаговым процессам уравнение Беллмана позволяет вместо оптимизации функции по всем переменным оптимизировать по шагам функцию одной переменной. Это требует меньшего количества операций по сравнению с прямой оптимизацией функции, но расходует больше памяти ЭВМ для хранения промежуточных результатов функций Беллмана.

Сетевое планирование • • 5. 1. Сетевая модель и ее основные элементы Сетевая модель представляет собой комплекс графических, логических и расчетных методов, позволяющих решать задачи, когда достижение конечной цели связано с осуществлением ряда взаимосвязанных работ (действий, мероприятий, операций), одни из которых можно выполнять одновременно, параллельно, а другие в определенной последовательности. Основным элементом модели является сетевой график. Сетевой график — это ориентированный граф без контуров, ребра которого имеют одну или несколько числовых характеристик. Он графически изображает последовательность выполнения комплекса взаимосвязанных достижение конечной цели. Наибольшее распространение способ задания сетевых графиков получил в следующих терминах: дуги графа — операции (работы), а вершины графа — события. Работа характеризует материальное действие, требующее использования ресурсов, или логическое действие, требующее лишь взаимосвязи событий. При графическом представлении изображается стрелкой, которая соединяет два события и обозначается парой упорядоченных чисел, заключенных в скобки (i, j), где i — номер события из которого стрелка, обозначающая работу, выходит, a j — номер события, в которое она входит. Работа представляет собой процесс, происходящий во времени, и имеет определенную продолжительность.

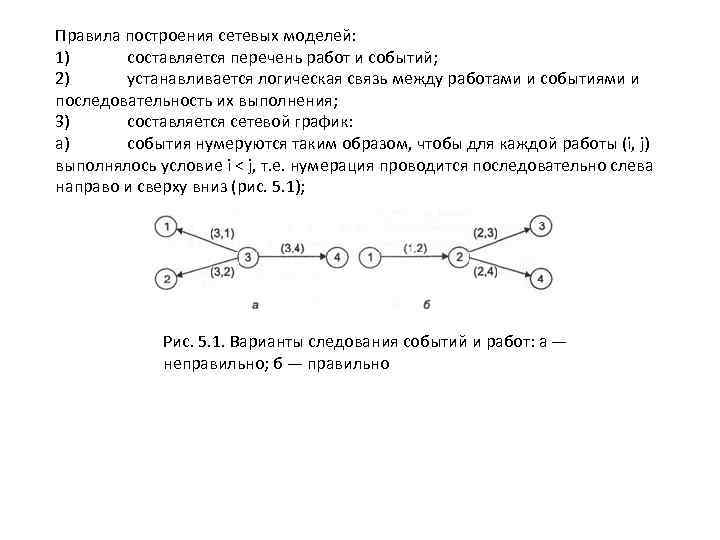Правила построения сетевых моделей: 1) составляется перечень работ и событий; 2) устанавливается логическая связь между работами и событиями и последовательность их выполнения; 3) составляется сетевой график: а) события нумеруются таким образом, чтобы для каждой работы (i, j) выполнялось условие i < j, т. е. нумерация проводится последовательно слева направо и сверху вниз (рис. 5. 1); Рис. 5. 1. Варианты следования событий и работ: а — неправильно; б — правильно

б) в сетевом графике не должно быть тупиковых событий, кроме завершающего, и событий, которым не предшествует хотя бы одна работа, кроме исходного; в) в сетевом графике не должно быть циклов; г) между одной парой событий можно изобразить только одну работу; д) всем стрелкам сетевого графика задают общее направление слева на право; е) при необходимости изображения двух параллельно выполняемых работ между двумя событиями вводят дополнительное промежуточное событие и фиктивную работу с нулевой продолжительностью (рис. 5. 2); Рис. 5. 2. Варианты изображения работ: а — неправильно; б — правильно 4) рассчитываются параметры событий и работ, определяются резервы времени и критический путь; 5) проводится анализ коэффициентов напряженности работ и оптимизации сетевого графика.

5. 2. Параметры сетевой модели и методы их расчета Введем следующие обозначения: i, j — номера событий; N — количество событий; (i, j) работа, соединяющая события i, j; t (i, j) — продолжительность работы, соединяющей события i и j; LKp — критический путь; tкр — продолжительность критического пути; Lп путь; tп — продолжительность пути Lп. Для каждого события сетевой модели рассчитывается следующие три показателя. 1. Ранний срок свершения j го события t п(j). Определяется величиной наиболее длинного пути, соединяющего исходное и j е событие. (5. 1)

2. Поздний срок свершения i го события tп(i). Характеризуется самый поздний срок, к которому должно совершиться i е событие, при котором все последующие события, в том числе завершающее, завершаются в установленные сроки: (5. 2) Этот показатель определяется методом «обратного хода» , начиная с завершающего события, с учетом соотношения tп(N) =tp(N). 3. Резерв i го события R(i) показывает, на какой максимально допустимый срок можно задержать наступление i го события, не нарушая сроков завершения всего комплекса работ: (5. 3) События, лежащие на критическом пути, имеют нулевой резерв времени. Для всех работ (i, j) на основе показателей событий сетевой модели (5. 1)—(5. 2) рассчитывается следующая группа параметров сетевой модели: 1. Ранний срок начала работы (i, j): (5. 4) 2. Ранний срок окончания работы (i, j): (5. 5)

3. Поздний срок начала работы (i, j): (5. 6) 4. Поздний срок окончания работы (i, j): (5. 7) 5. Полный резерв времени работы (i, j) Rn(i, j) показывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится: (5. 8) (5. 9) 6. Частный резерв времени первого вида: или (5. 10) R(i, j) часть полного резерва времени (увеличения продолжительности работы), на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее исходного события. 7. Частный резерв времени второго вида (свободный резерв) Rc(i, j) это часть полного резерва времени, на которую можно увеличить продолжительность работы или отсрочить ее начало, не изменив при этом ранних сроков начала последующих работ: или (5. 11)

8. Независимый резерв времени RH(i, j) соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки: RH(i, j)=max{0; tp(j) tп(i) t(i, j)}=max{0, Rп(i, j) R(i) R(j)} (5. 12)

Использование этого резерва не влияет на величину резервов времени других работ. Путь сетевой модели характеризуется двумя показателями: 1. Продолжительность пути tп определяется суммой продолжительностей составляющих его работ. 2. Резерв времени пути Rп показывает, на сколько может увеличиться продолжительность работ, составляющих путь Lп, без изменения продолжительности общего срока выполнения всех работ: Работы, лежащие на критическом пути, резервов времени не имеют. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ KH(i, j). Если совпадающую с критическим путем величину отрезка пути обозначить как t'Kр, а протяженность максимального из некритических путей, проходящих через данную работу, tmax(i, j), то (5. 14) Коэффициент напряженности работы можно рассчитать и через резерв времени: (5. 15)

Коэффициент напряженности изменяется от 0 до 1, причем он ближе к 1, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых он равен 1. На основе этого коэффициента все работы разделяются на три группы: 1) напряженные, когда Kн(i, j) > 0, 8; 2) подкритические, когда 0, 6 < Kн(i, j) < 0, 8; 3) резервные, когда Kн(i, j) < 0, 6. Оптимизация сетевой модели заключается в перераспределении ресурсов с напряженных работ на критические, в результате чего максимально уменьшается общая продолжительность работ и все переводится в первую группу.

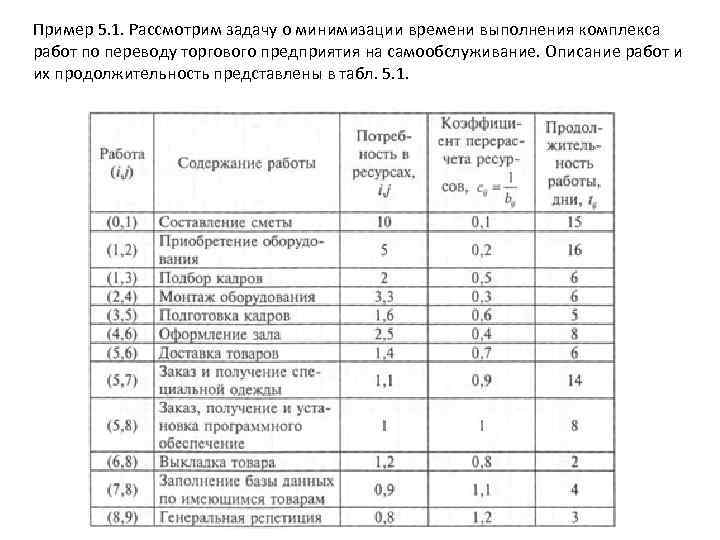Пример 5. 1. Рассмотрим задачу о минимизации времени выполнения комплекса работ по переводу торгового предприятия на самообслуживание. Описание работ и их продолжительность представлены в табл. 5. 1.

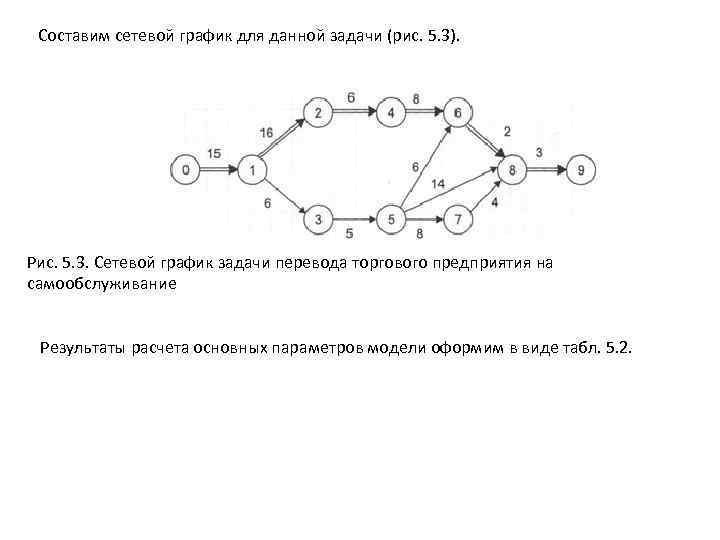Составим сетевой график для данной задачи (рис. 5. 3). Рис. 5. 3. Сетевой график задачи перевода торгового предприятия на самообслуживание Результаты расчета основных параметров модели оформим в виде табл. 5. 2.

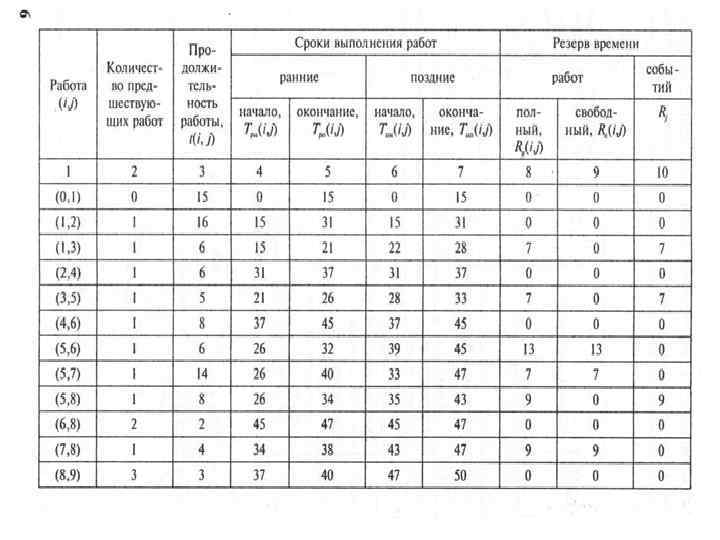
Правила заполнения табл. 5. 2: • столбцы 1 и 3 заполняются на основе исходных данных, представленных в табл. 5. 1; • в столбце 2 записывается количество предшествующих работ, которое определяется либо по сетевому графику рис. 5. 3, либо из столбца 1: определяем число работ, имеющих одинаковый номер завершения среди всех пар (i, j), например (4, 6) и (5, 6), и записываем это число (т. е. 2) в столбце 2 против работы (6, 8), т. е. количества предшествующих работ; • в столбце 4 раннее начало работ, выходящих из исходного состояния, равно 0. Раннее начало последующих работ равно максимальному сроку раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ в столбце 2. Расчет показателей этого столбца проводится после расчета раннего окончания предшествующих работ, т. е. заполнения предшествующих строк столбца 5; • в столбце 5 раннее окончание работ, выходящих из исходного события, равно их продолжительности. Ранее окончание последующих работ равно сумме величин раннего начала и продолжительности данной работы, т. е. значение столбца 5 равно сумме значений столбцов 3 и 4; • перед заполнением столбца 7 необходимо рассчитать продолжительность критического пути как максимум из сроков раннего окончания работ, ведущих к завершающему событию 9 (в нашем случае это шах{40+3; 47+3; 38+3} = 50 дн. );

• заполнение столбца 7 ведется снизу вверх. Для всех работ, ведущих к завершающему событию, позднее окончание равно продолжительности критического пути (T по(8, 9) = 50). Затем находятся предшествующие работы; поздний срок их окончания будет равен разности позднего срока окончания текущей работы и продолжительности текущей работы (например, Тпо(7, 8) = = Тпо(8, 9) t 89 = 50 3 = 47); • столбец 6 заполняется после столбца 7. Позднее начало работы определяется как разность между поздним сроком окончания работы и ее продолжительностью, т. е. значение столбца 6 равно разности значений столбцов 7 и 3; • в столбце 8 полный резерв времени работы определяется как разность между значениями столбцов 7 и 5. Если эта разность равна 0, то работа является критической; • в столбце 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося собы¬тием j столбца 7, и поздним началом работы, начинающейся событием j столбца 4 (например, R 9 = Tпн(8, 9)— Tпо(5, 8) = = Tпн(8, 9) Tпо(6, 8) = Tпн(8, 9) TП 0(7, 8) = 47 47 = 0); • в столбце 9 свободный резерв времени работы определяется как разность значений столбцов 10 и 8 и указывает на расположения резервов, необходимых для оптимизации. Для определения резервов времени составим все возможные пути перехода из исходного события (0) к завершающему (9).

Таких путей четыре: Определим длительность этих путей:

Найдем длину критического пути: Определим полные резервы времени по всем путям, используя формулу (5. 13):

Рассчитаем коэффициенты напряженности. Для работ критического пути L 1 они будут равны 1, для других работ определим их значение, используя формулу (5. 15), в результате получим: (5. 15) В соответствии с полученным значением коэффициентов напряженности можно утверждать, что оптимизация в сетевой мо¬дели возможна за счет свободных резервов работ (5, 6), (5, 8) и (7, 8), а также за счет остальных резервов работ (1, 3), (3, 5) и (5, 7).

КОМБИНАТОРНЫЕ ЗАДАЧИ • Сложность вычислений минимума функции от п переменных f(x 1, x 2, . . xn) оценивают как Cn 3. Такая оценка связана с тем, что для решения эквивалентной задачи решения уравнения f(x 1, x 2, …Xп) = 0 требуется именно это количество операций. Однако если вектор х может принимать только целочисленные значе ния, то для функции отсутствует понятие градиента и основанные на нем методы оптимизации не работают. Можно попытаться погрузить дискретную задачу в непрерывную с некоторым прибли жением и полученное решение округлить до ближайшего целого. Однако функция при этом подходе может не принимать оптимального значения, а вектор х не удовлетворять ограничениям. В общем случае приходится прибегать к перебору вариантов, сложность решения подобных задач растет экспоненциально с ростом размерности вектора х9 и такие задачи называют неполиномиально сложными задачами. Примером является задача коммивояжера.

Постановка задачи коммивояжера • • Имеется п городов а 1. . . , ап. Задана матрица затрат с = {сij}, i, j = 1, …, n. Коммивояжеру нужно выехать из городаа 1 объехать все пункты и вернуться в начальный город так, чтобы где хij (3. 1) • где х неизвестные величины, формирующие маршрут: ij (3. 2) В город можно въехать и выехать только один раз, поэтому (3. 3)

• Геометрическая интерпретация задачи коммивояжера дана на рис. 3. 1. Рис. 3. 1. Графическое представление задачи коммивояжера Здесь по оси у номера городов, по оси х номера шагов коммивояжера. Так же как в задаче ДП об инвестициях, в зада че коммивояжера необходимо найти ломаную оптимальной длины, соединяющую точку на начальной прямой с заданной точкой на конечной прямой. Однако применить метод последовательного ана лиза вариантов здесь невозможно. Пусть коммивояжер находится в 4 м городе. Его дальнейшее поведение зависит от способа, которым он попал в данный город. Если из города 1 в город 3 он двигался по сплошной линии, ему запрещено в дальнейшем заходить в 3 й город, если по пунктирной линии, то во 2 й город. Таким образом, путь коммивояжера зависит не только от текущего состояния, как в задаче динамического программирования, но и от предыстории то го, каким образом он попал в это состояние. Подсчитаем количество вариантов при прямом переборе.

• • • Подсчитаем количество вариантов при прямом переборе. Если рассматривать конкретную задачу, проще будет подсчитать, сколько требуется операций: на 1 м шаге существует п — 1 вариантов перехода в остальные города, на первых двух шагах количество вариантов равно (п — 1)(n — 2), а на п шагах получаем (п — 1)! вариантов. Для таких задач используется метод ветвей и границ (попытка упорядочить перебор). Метод ветвей и границ Пусть Mo множество всех вариантов решения задачи перебо ра. Разобьем это множество на подмножества Mi так, чтобы эти подмножества охватывали все варианты, и чтобы каждый вариант входил только в одно подмножество, т. е. чтобы выполнялись условия Если продолжить такое разбиение для каждого из подмножеств, то в итоге построим дерево, корень которого содержит все варианты, а конечные ветви содержат единственный вариант. Если можно оценить снизу или сверху решения, содержащиеся в каждом подмножестве (определить функцию оценки соответственно), то для сокращения перебора можно применить метод ветвей и границ.

• • Метод содержит три этапа: ветвление, оценку и отбрасывание вариантов. Если удалось ввести функцию оценки, то после ветвления множества MQ оцениваем решения во множествах. Mi и дальнейшее ветв ление производится для наиболее перспективного множества с максимальной или минимальной оценкой в надежде, что именно там содер жится оптимальное решение. Так Рис. 2. Дерево вариантов 3 продолжаем до тех пор, пока в мнокомбинаторной задачи в множестве не окажется единственное решение (рис. 3. 2). • Процедура отбрасывания вариантов в задаче минимизации основана на следующих принципах. По уже достигнутому значению функцииf 0, полученному на некотором этапе расчетов. Пусть имеем вариант решения со значением функции f =f°. Тогда все множества, для которых оценка , не могут содержать лучших значений функции и должны быть отброшены. По предельному значению функции. В этом случае если достигнута граница значений функции, например, нулевая ошибка, то • •

• • лучшего решения не может быть. Часто отбрасывают остальные решения, если полученное решение удовлетворяет ЛПР. 3. По сравнению оценок. Пусть для двух множеств М 1 и М 2 получены оценки Если выполняется неравенство , то во множестве М 1 нет лучших решений, чем во множестве M 2 Рассмотрим применение метода ветвей и границ для задачи коммивояжера на конкретном примере. 3. 3. Решение задачи коммивояжера Коммивояжеру нужно посетить 5 городов, затраты на переход из города i в город j заданы матрицей, изображенной на рис. 3. 3 (знак # означает запрещение перехода). Рис. 3. 3. Матрица затрат в задаче коммивояжера

• Алгоритм метода ветвей и границ применительно к задаче коммивояжера 1. Оценка вариантов. Пусть G(0) множество всех вариантов задачи. Вычислим оценку этого множества. Рассмотрим конкретный цикл с номерами городов i 1, i 2, . . . , in. Затраты в таком цикле будут следующими: Определим числа Эти числа представляют собой минимальные затраты на переход из города i во все другие города (рис. 3. 4). Рис. 3. 4. Минимальные затраты на выход из каждого города

• • Так как из каждого города нужно выйти, суммарные затраты составят не меньше чем h = ∑hi Вычтем эти числа из каждого элемента матрицы затрат Очевидно, что теперь суммарные затраты составят Матрица затрат показана на рис. 3. 5. Рассмотрим минимальные величины по столбцам Эти числа представляют собой минимальные затраты на вход в город j. Так как в каждый город нужно войти есть минимальные затраты на всем пути (рис 3, 6),

• • Матрица называется приведенной матрицей, и значение функции через элементы этой матрицы будет следующее: Очевидно, что оценка Матрица представлена на рис. 3. 7. Здесь Рис. 3. 7. Приведенная матрица затрат

• • Зададим множество где v номер шага, к варианты множеств решений в задаче коммивояжера: k = 1, i →j множество всех маршрутов, содержащих путь из города i в город j; k = 2, i ≠ →j множество всех маршрутов, не содержащих путь из города i в город j. В группу 1 включаем такой переход, который характеризуется минимальными (нулевыми) затратами. Поскольку таких переходов несколько (в данном случае 8), то среди нулевых элементов приведенной матрицы затрат выбираем такой путь, чтобы в группу 2 попали варианты с наибольшими затратами. Тогда для этих двух множеств будут получены оценки, максимально отличающиеся друг от друга Выбираем пару городов (r, m), для которых Если таких пар несколько, определяем числа = αr + βm. Первое слагаемое в сумме характеризует минимальные затраты на выход из города r (переход из r в т запрещен), второе слагаемое минимальные затраты на вход в город т при этом же условии. Сумма этих чисел дает минимальные затраты для множества маршрутов, не содержащих переход из r в т. Приведем результаты вычислений этих затрат (рис. 3. 8).

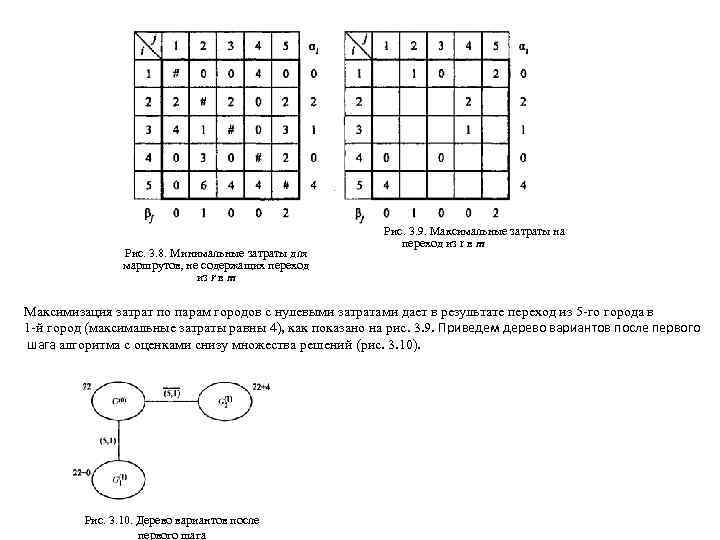Рис. 3. 8. Минимальные затраты для маршрутов, не содержащих переход из r в т Рис. 3. 9. Максимальные затраты на переход из r в т Максимизация затрат по парам городов с нулевыми затратами дает в результате переход из 5 го города в 1 й город (максимальные затраты равны 4), как показано на рис. 3. 9. Приведем дерево вариантов после первого шага алгоритма с оценками снизу множества решений (рис. 3. 10). Рис. 3. 10. Дерево вариантов после первого шага

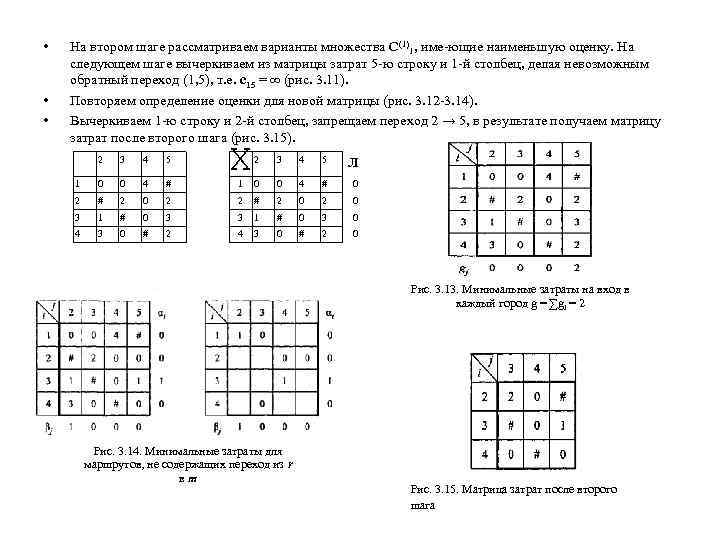• • • На втором шаге рассматриваем варианты множества C(1)1, име ющие наименьшую оценку. На следующем шаге вычеркиваем из матрицы затрат 5 ю строку и 1 й столбец, делая невозможным обратный переход (1, 5), т. е. c 15 = ∞ (рис. 3. 11). Повторяем определение оценки для новой матрицы (рис. 3. 12 3. 14). Вычеркиваем 1 ю строку и 2 й столбец, запрещаем переход 2 → 5, в результате получаем матрицу затрат после второго шага (рис. 3. 15). X 2 3 4 5 Л 1 0 0 4 # 0 2 2 # 2 0 0 3 3 1 # 0 3 0 # 2 4 3 0 # 2 0 2 3 4 5 1 0 0 4 # 2 0 3 1 # 4 3 0 Рис. 3. 13. Минимальные затраты на вход в каждый город g = ∑gi = 2 Рис. 3. 14. Минимальные затраты для маршрутов, не содержащих переход из r в т Рис. 3. 15. Матрица затрат после второго шага

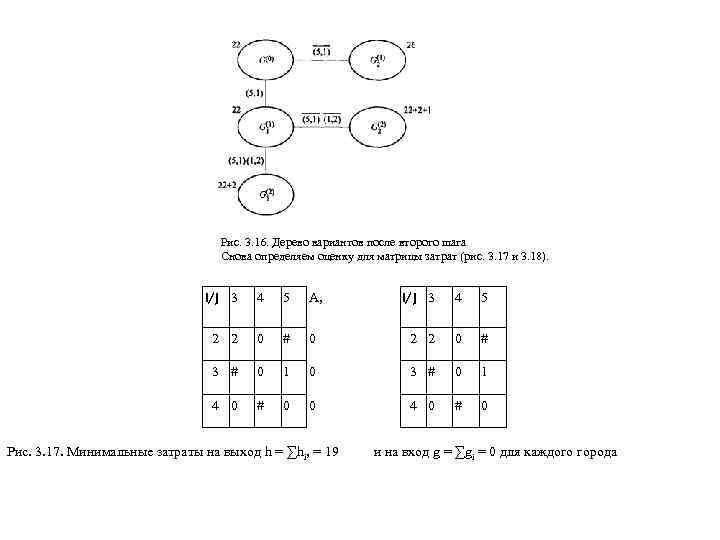Рис. 3. 16. Дерево вариантов после второго шага Снова определяем оценку для матрицы затрат (рис. 3. 17 и 3. 18). i/j 3 4 5 А, i/j 3 4 5 2 2 0 # 0 2 2 0 # 3 # 0 1 0 3 # 0 1 4 0 # 0 0 4 0 # 0 Рис. 3. 17. Минимальные затраты на выход h = ∑hi, = 19 и на вход g = ∑gi = 0 для каждого города

• • Вычеркиваем 2 ю строку, 4 й столбец, запрещаем переход 4 —► 5 и получаем матрицу затрат на последнем шаге (рис. 3. 19). Остается единственный вариант 4 —► 3 —► 5 —► 1 (стоимость равна 1). Полный замкнутый путь: 5+1—>2—>4—>3+5 с затратами 3+3 + 4 + 5 + 10 = 25. Сравнивая полученное решение с оценками множеств G(v)2 приходим к выводу, что лучшего решения в этих множествах нет, и они могут быть отброшены (рис. 3. 20). i/j 3 5 3 4 5 2 2 0 # 2 3 # 1 3 # 0 1 1 4 0 # 0 0 h 2 0 1 Рис. 3. 18. Минимальные затраты для маршрутов, не содержащих переход из r в т Рис. 3. 19. Матрица затрат на последнем шаге

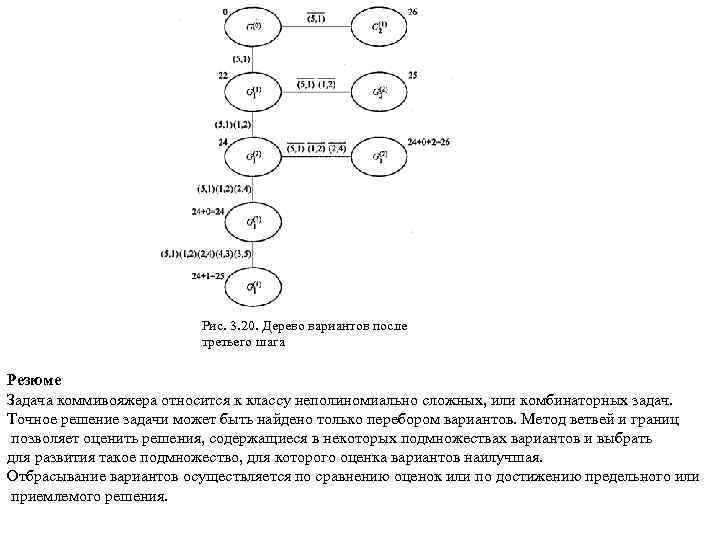Рис. 3. 20. Дерево вариантов после третьего шага Резюме Задача коммивояжера относится к классу неполиномиально сложных, или комбинаторных задач. Точное решение задачи может быть найдено только перебором вариантов. Метод ветвей и границ позволяет оценить решения, содержащиеся в некоторых подмножествах вариантов и выбрать для развития такое подмножество, для которого оценка вариантов наилучшая. Отбрасывание вариантов осуществляется по сравнению оценок или по достижению предельного или приемлемого решения.