Методы обоснования реальных инвестиций Лекция 15 1

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕГИСТРАЦИЯ

Методы обоснования реальных инвестиций Лекция 15 1

Вопросы: 1. Критерии и методы оценки инвестиционных проектов 2. Противоречивость критериев оценки 2

Рекомендуемая литература Финансовый менеджмент: теория и практика. В. В. Ковалёв. Издательство «Проспект» . М. , 2008 – 1024 с. l Стр. 605 – 623 l Финансовый менеджмент. Ю. М. Бахрамов, В. В. Глухов. Издательство «Лань» . СПб – М – Краснодар, 2006 – 734 с. l Стр. 177 – 212 l 3

1. Критерии и методы оценки инвестиционных проектов В основе принятия управленческих решений инвестиционного характера – оценка и сравнение объёмов инвестиций и будущих денежных поступлений Сравниваемые показатели относятся к разным моментам времени => ключевой проблемой является их сопоставимость Под критериями оценки инвестиционных проектов понимаются показатели, используемые для: а) для отбора и б) оптимизации в) формирования ранжирования эксплуатации оптимальной инвестиционной проекта программы В анализе инвестиционной деятельности используются: Критерии, основанные на дисконтированных оценках учётных оценках (фактор времени учитывается) (фактор времени не учитывается) 4

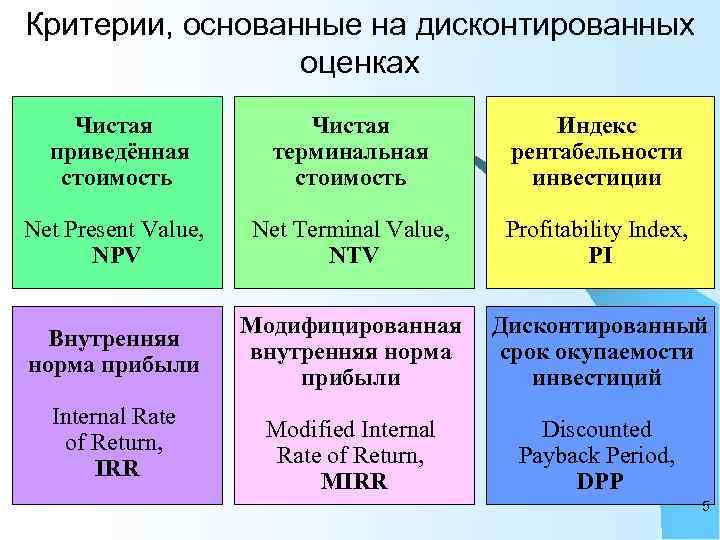
Критерии, основанные на дисконтированных оценках Чистая приведённая стоимость Чистая терминальная стоимость Индекс рентабельности инвестиции Net Present Value, NPV Net Terminal Value, NTV Profitability Index, PI Внутренняя норма прибыли Модифицированная внутренняя норма прибыли Дисконтированный срок окупаемости инвестиций Modified Internal Rate of Return, MIRR Discounted Payback Period, DPP Internal Rate of Return, IRR 5

Критерии, основанные на учётных оценках Срок окупаемости инвестиции Payback Period, PP Учётная норма прибыли Accounting Rate of Return, ARR 6

Важные замечания 1. Ни один критерий не может рассматриваться как безусловный и неоспоримый аргумент => Принятие решения в отношении такого сложного явления, как инвестиционный проект, должно основываться на комплексе доводов, в числе которых могут быть один или несколько формализованных критериев 2. Русскоязычная терминология в разделе управления инвестиционными проектами, не устоялась => В литературе встречаются и другие наименования критериев: NPV «чистая дисконтированная стоимость» , «чистый приведённый эффект» , «чистая настоящая стоимость» , IRR «внутренняя норма доходности» , «внутренняя норма рентабельности» , «внутренняя норма окупаемости» , ARR «расчётная норма прибыли» и др. 7

Метод расчёта чистой приведённой стоимости Чистая приведённая стоимость (NPV) – разность суммы элементов возвратного потока и исходной инвестиции, дисконтированных к началу действия ожидаемого проекта Разовое инвестирование n NPV = ∑[CFk / (1 + r)k] – IC k=1 Последовательное инвестирование в течение m лет n m k=1 j=1 NPV = ∑[CFk / (1 + r)k] – ∑[ICj/(1 + i)j] CFk – годовые доходы (чистые денежные поступления); k, j – порядковый номер года; r – ставка дисконтирования; 8 IC – исходная инвестиция

Метод расчёта чистой приведённой стоимости NPV < 0, ценность компании уменьшится => проект следует отклонить NPV > 0, ценность компании увеличится => проект следует принять NPV = 0, ценность компании не изменится => нужны дополнительные аргументы для принятия Обычно r постоянна, но может изменяться по годам Для менеджмента проект с NPV = 0 может быть привлекателен, поскольку ведёт к увеличению масштаба компании При прогнозировании доходов по годам необходимо учитывать все виды поступлений (ликвидационная стоимость оборудования, высвобождение части оборотных средств и т. п. ) Необходимо также учитывать оттоки средств в соответствующем году (затраты по ликвидации связанных с проектом последствий: восстановление экологии, затраты на вывоз оборудования и т. п. ) 9

Метод расчёта чистой приведённой стоимости Пример. Проанализировать проект со следующими характеристиками: – 150, 30, 70, 45 млн. руб. Возможны два случая: 1) стоимость капитала постоянна и равна 12%; 2) стоимость капитала меняется по годам: 12%, 13%, 14% Воспользуемся формулой: n NPV = ∑[CFk / (1 + k] r) – IC k=1 1) NPV = – 150 + 30/1, 12 + 70/1, 123 + + 45/1, 124 = 11, 0 NPV > 0, т. е. проект является приемлемым 2) NPV = – 150 + 30/1, 12 + 70/1, 12· 1, 13· 1, 14 + 45/1, 12· 1, 13· 1, 142 = – 12, 0 NPV < 0, т. е. проект не приемлем 10

Метод расчёта чистой терминальной стоимости Чистая терминальная стоимость (NTV) – разность суммы элементов возвратного потока и исходной инвестиции, наращённых к моменту окончания оцениваемого проекта n n-k NTV= ∑[CFk • (1 + r) ] – IC • (1 + r) n k=1 NTV < 0, проект следует отклонить NTV > 0, проект следует принять NTV = 0, нужны дополнительные аргументы Критерии NPV и NTV взаимообратны: NTV = NPV(1 + r)n NPV = NTV/(1 + r)n В условиях предыдущего примера имеем: NTV = – 150· 1, 124 + 30· 1, 123 + 70· 1, 122 + 70· 1, 12 + 45=17, 33 млн. руб. 11 n = 17, 33 · 0, 6355 = 11, 0 млн. руб. NPV = NTV · 1/(1 + r)

Метод расчёта индекса рентабельности инвестиции Индекс рентабельности инвестиции (PI) – это отношение суммы дисконтированных элементов возвратного потока к исходной инвестиции n PI ={∑[CFk / (1 + r)k]} / IC k=1 PI < 1, проект является убыточным, следует отклонить PI > 1, проект является прибыльным, следует принять PI = 1, проект не является ни прибыльным, ни убыточным PI относительный показатель: характеризует уровень доходов на единицу затрат, т. е. эффективность вложений 12

Метод расчёта индекса рентабельности инвестиции Критерий PI очень удобен при выборе: - одного проекта из альтернативных, имеющих примерно одинаковое значение NPV (например, одинаковые NPV, но разные объёмы требуемых инвестиций) - при комплектовании портфеля инвестиций с целью максимизации суммарного значения NPV - при комплектовании портфеля инвестиций в случае ограничения по объёму источников финансирования Последовательность действий : 1) независимые проекты упорядочивают по убыванию PI; 2) в портфель последовательно включают проекты с наибольшими значениями PI; 3) подтверждают расчётом оптимальность полученного портфеля 13 (с позиции максимизации совокупного NPV)

Метод расчёта внутренней нормы прибыли инвестиции Внутренняя норма прибыли (IRR) используется для оценки инвестиции и численно равна значению ставки дисконтирования, при которой чистая приведённая стоимость инвестиционного проекта (NPV) равна нулю Доходность инвестиций через один год определяется легко: NPV = CF 1/(1 + r) – IC = 0 => r = (CF 1/IC) – 1 Величина IRR инвестиционного проекта продолжительностью n лет вычисляется из следующего выражения: NPV = C 1/(1 + IRR) + C 2/(1 + IRR)2 + … + Cn/(1 + IRR)n – IC = 0 Для уравнений пятой степени и выше, как доказал Н. Абель в 1824, нет общей формулы, которая выражала бы корни уравнения через его коэффициенты, => алгебраические методы 14

Метод расчёта внутренней нормы прибыли инвестиции n NPV=f(r)=∑[CFk/(1 + r)k] – IC=0 k=1 n или NPV = f(r) = ∑[CFk / (1 + r)k] k=0 y = f(r) = NPV n y = ∑CFk k=0 IRR – 1 r График функции y = f(r) = NPV для наиболее типовой ситуации, когда единовременный отток (IC) сменяется серией притоков (CFk), в сумме превосходящих IC (классический проект) Классический проект – однократное пересечение графиком оси абсцисс Ввиду нелинейности функции и возможных комбинаций знаков элементов денежного 15 потока функция может иметь несколько точек пересечения с осью абсцисс

Метод расчёта внутренней нормы прибыли инвестиции IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом IRR сравнивается со стоимостью капитала, CC (конкретного источника финансирования, WACC) а) если IRR > CC, то проект следует принять; б) если IRR < CC, то проект следует отвергнуть; в) если IRR = CC, то нужны дополнительные аргументы Показатель IRR даёт характеристику резерва безопасности. Большее значение IRR считается предпочтительным Если значения ожидаемых доходов (особенно последних периодов) были завышены, значение IRR может снизиться (например, с 60% до 45%), но всё ещё оставаться высоким для нормального уровня 16 процентных ставок

Расчёт IRR методом линейной аппроксимации IRR находят путём последовательных итераций с использованием различных значений дисконтирующих множителей 1/(1 + r)n Для этого рассчитывают (выбирают по финансовым таблицам) два значения r 1 < r 2 так, чтобы в интервале (r 1, r 2) функция NPV для данной ставки r, меняла своё значение с «+» на «– » , или с «– » на «+» Далее применяют формулу: IRR' = r 1 + {NPV(r 1)/[NPV(r 1) – NPV(r 2)]}(r 1 – r 2) r 1 - значение ставки дисконтирования, при которой NPV(r 1) > 0 (NPV(r 1) < 0), r 2 - значение ставки дисконтирования, при которой NPV(r 2) < 0 (NPV(r 2) > 0) 17

Расчёт IRR методом линейной аппроксимации Пример. Проект рассчитан на 3 года, требует инвестиций в размере 10 млн. руб. , имеет предполагаемые денежные поступления в размере 3 млн. руб. , 4 млн. руб. , 7 млн. руб. Определить значение IRR Решение. Возьмём два произвольных значения ставки дисконтирования: r 1 = 10%, r 2 = 20% Соответствующие расчёты с использованием значений, найденных по финансовой таблице 2 Приложения 3 (Ковалёв В. В. Финансовый менеджмент) приведены в таблице Для уточнения значения IRR выполняется вторая аппроксимация для значений ставки дисконтирования r 1 = 16%, r 2 = 17% 18

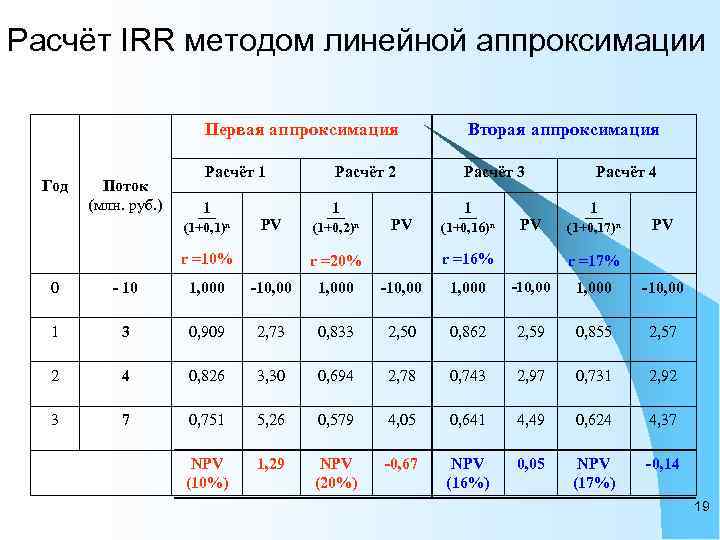
Расчёт IRR методом линейной аппроксимации Первая аппроксимация Год Поток (млн. руб. ) Вторая аппроксимация Расчёт 1 Расчёт 3 1 — (1+0, 1)n PV r =10% Расчёт 2 1 — (1+0, 2)n PV 1 — (1+0, 16)n PV r =16% r =20% Расчёт 4 1 — (1+0, 17)n PV r =17% 0 - 10 1, 000 -10, 00 1 3 0, 909 2, 73 0, 833 2, 50 0, 862 2, 59 0, 855 2, 57 2 4 0, 826 3, 30 0, 694 2, 78 0, 743 2, 97 0, 731 2, 92 3 7 0, 751 5, 26 0, 579 4, 05 0, 641 4, 49 0, 624 4, 37 NPV (10%) 1, 29 NPV (20%) -0, 67 NPV (16%) 0, 05 NPV (17%) -0, 14 19

Расчёт IRR методом линейной аппроксимации Вычисляем значение IRR в первом приближении по формуле: IRR' = r 1 + {NPV(r 1)/[NPV(r 1)–NPV(r 2)]}(r 1 – r 2)= 0, 1 + {1, 29/[1, 29 – (– 0, 67)]}·(0, 2 – 0, 1)= 0, 166 = 16, 6% По данным второй аппроксимации уточняем значение IRR: IRR' = r 1 + {NPV(r 1)/[NPV(r 1)–NPV(r 2)]}(r 1 – r 2)= 0, 16 + {0, 05/[0, 05 – (– 0, 14)]}·(0, 17 – 0, 16)=0, 1626=16, 26% Истинное значение показателя IRR в данном случае равно 16, 23% С практической точки зрения такая точность является излишней 20

Метод определения срока окупаемости инвестиций Срок окупаемости инвестиции (PP) предусматривает расчёт числа базисных периодов, за которое произойдёт возмещение сделанных инвестиционных расходов без учёта фактора времени Один из самых распространённых методов в мировой учётно-аналитической практике Если доход распределён по годам равномерно, то PP находится делением единовременных затрат на величину годового дохода Если прибыль распределена неравномерно, то срок окупаемости рассчитывается прямым подсчётом числа лет, в течение которых инвестиция будет погашена кумулятивным доходом Общая формула подсчёта показателя PP имеет вид: n PP = min n, при котором ∑CFk ≥ IC k=1 где CFk – поступления по годам, n ≤ m; m – срок продолжительности проекта Нередко показатель рассчитывается более точно, т. е. с дробной частью года Например, для потока – 100, 40, 40, 30, 20 млн. руб. PP = 3 года (расчёт до целого года) 21 PP = 2, 5 года (точный расчёт)

Метод определения дисконтированного срока окупаемости инвестиций Дисконтированный срок окупаемости инвестиций (DPP) – расчёт числа базисных периодов, за которое произойдёт возмещение сделанных инвестиционных расходов с учётом фактора времени n DPP = min n, при котором ∑[CFk / (1 + r)k] ≥ IC k=1 В качестве ставки дисконтирования r может использоваться средневзвешенная стоимость капитала WACC Всегда DPP ≥ PP Проект приемлемый по РР может оказаться неприемлемым по DPP Критерии PP и DPP могут использоваться двояко: 1) проект принимается, если окупаемость имеет место 2) проект принимается, если срок окупаемости меньше, чем некоторый плановый срок Как правило, проекты со сроком погашения, превышающим 4 года, не принимаются 22

Недостатки показателя срока окупаемости 1) Не учитывает влияние доходов последних периодов Например, два проекта с одинаковыми капитальными затратами (10 млн. руб. ), но разными прогнозируемыми годовыми доходами: - проект А генерирует 4, 2 млн. руб. в год в течение 3 лет, - проект В генерирует 3, 8 млн. руб. в год в течение 10 лет Оба проекта обеспечивают окупаемость в течение 3 лет => с позиции данного критерия они равноправны. Однако очевидно, что проект В более выгоден 2) Поскольку метод РР основан на недисконтированных оценках, он не делает различия между проектами с одинаковой суммой кумулятивных доходов, но разным распределением по годам Например, проект А с годовыми доходами 40, 60, 20 млн. руб. проект В с годовыми доходами 20, 40, 60 млн. руб. С позиции данного критерия проекты равноправны, но очевидно, что проект А предпочтителен, поскольку обеспечивает, 23 большую сумму доходов в первые два года

Преимущества показателя срока окупаемости В отличие от критериев NPV, IRR, PI, критерий срока окупаемости инвестиций позволяет получить оценки (хотя и грубые) о ликвидности и рисковости проекта Понятие ликвидности здесь условно означает как можно более быстрое возмещение сделанных капиталовложений Менее рисков тот проект, у которого меньше срок окупаемости, поскольку денежные поступления удалённых от начала проекта лет трудно прогнозируемы, т. е. более рисковы по сравнению с поступлениями первых лет 24

Метод расчёта учётной нормы прибыли Учётная норма прибыли (ARR), называемая также коэффициентом эффективности инвестиции, предусматривает сопоставление средних значений прибыли и инвестиции Особенности метода: 1) он не предполагает дисконтирования показателей дохода; 2) доход характеризуется показателем чистой прибыли 3) показатель чаще всего сравнивается с некоторой модификацией коэффициента рентабельности активов ROA = PN/A, Возможно установление специального порогового значения ROA с которым будет сравниваться ARR, или даже системы пороговых значений, дифференцированной по - видам проектов, - степени риска, 25 - центрам ответственности и др.

Метод расчёта учётной нормы прибыли Существуют разные алгоритмы исчисления ARR, наиболее распространённый: ARR = PN/[1/2·(IC + RV)] PN – среднегодовая величина чистой прибыли; IC – величина инвестиции; RV – остаточная (ликвидационная) стоимость проекта Алгоритм расчёта показателя исключительно прост => широкое применение на практике Пример использования описанных критериев (В. В. Ковалёв, стр. 619)26

Недостатки показателя учётной нормы прибыли Метод не делает различия между проектами с одинаковой суммой среднегодовой прибыли, но варьирующей суммой прибыли по годам Метод не делает различия между проектами, имеющими одинаковую среднегодовую прибыль, но генерируемую в течение разного количества лет 27

2. Противоречивость критериев оценки В зависимости от выбора критериев эффективности проекта могут быть сделаны диаметрально противоположные выводы Например, согласно критериям NPV, PI и IRR проект надо отвергнуть; согласно двум другим критериям PP, ARR – принять Расхождения могут возникнуть не только между критериями разных групп (основанных на дисконтированных и недисконтированных оценках), но и внутри группы однородных критериев Необходимо ориентироваться на какой-то один или несколько критериев (наиболее важных по мнению руководства компании), => либо принять во внимание дополнительные объективные и субъективные факторы Исследования показали, что в случае противоречия между критериями более предпочтительно использование критерия NPV (исходя из максимизации благосостояния владельцев бизнеса) 28

Противоречивость критериев оценки Но на практике рекомендация о предпочтении NPV не является доминирующей: менеджеры американских компаний предпочитают критерий IRR критерию NPV в отношении 3: 1 Предположения, объясняющее эту ситуацию: - решения в области инвестиций легче принимать, основываясь на относительных, а не абсолютных оценках -применение IRR изначально не требует знания стоимости капитала (безусловно на конечном этапе она нужна для выбора проекта), которая может меняться - критерий IRR даёт возможность получить довольно быструю оценку степени рисковости проекта 29

Противоречивость критериев оценки Распространённая ошибка: выбирается тот проект, у которого выше показатель IRR Рассмотрим пример: Стоимость капитала для компании составляет 12% Имеется возможность инвестировать средства в проекты А и B, основные параметры этих проектов приведены в таблице Проект Денежные потоки по проектам, руб. I CF 1 CF 2 А - 1 000 305 000 B - 500 000 160 000 A–B - 500 000 145 000 CF 3 NPV, руб. IRR % 305 000 100 906 16 160 000 76 768 18 145 000 23 138 13, 9 CF 4 CF 5 305 000 160 000 145 000 Предпочтение следует отдать проекту А, т. к. это означает принятие проекта В с инвестициями в сумме 500 000 руб. и IRR = 18% и проекта (А – В) с инвестициями 500 000 руб. и IRR = 13, 9%, т. е. в дополнение к проекту В мы реализуем ещё один проект (А – В) 30 Средняя IRR полной корзины проектов A = B + (A – B) равна 16%

Скачать презентацию Методы обоснования реальных инвестиций Лекция 15 1

15. Методы обоснования реальных инвестиций.ppt

Количество слайдов: 30