Методы математической физики в геофизике Литература 1 Арамович

Методы математической физики в геофизике Литература: 1. Арамович И. Г. , Левин В. И. Уравнения математической физики. 2. Тихонов А. Н. , Самарский А. А. Уравнения математической физики. 3. Шамолин М. В. Высшая математика, Раздел XIV Уравнения математической физики. 4. Кудрявцев Л. Д. Математический анализ. Глава 7. Ряды фурье. Интеграл Фурье. 5. Данко П. Е. , Попов А. Г. Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Глава VI. Понятие об уравнениях в частных производных. 6. Демидович Б. П. Кудрявцев В. А. Краткий курс высшей математики. Глава XXI Ряды. Параграфы: 17, 18, 19. Глава XXII. Дифференциальные уравнения. Параграфы: 15, 16, 17. 7. Писменный Д. Конспект лекций по высшей математике. Глава XV Ряды Фурье. Интеграл Фурье. 8. Смирнов М. М. Задачи по уравнениям математической физики

Уравнение Пуассона: ΔU = ρ(M), где U(M) - гравитационный или магнитный потенциал, ρ(M) - избыточная плотность или фиктивные магнитные заряды, grad U(М) Δg ρ(M) E U div [σ(М) grad U] = - div j 0 где j 0 - плотность тока заданного источника, σ(M) - распределение удельной проводимости в Земле. σ(М) Пусть p = (p 1, р2, . . . , pn) - параметры модели, причем р ∈ Р, где P - множество допустимых значений параметров модели. U(x, p) х U(х, p) = Аx[p], Uэ(х) p = pmin p где Аx U(х, p) от Uэ(х)

Дифференциальные уравнения с частными производными. у' = f(x, у) у" = f(х, у, у') у = φ(х, С) y = φ(x, C 1, C 2) у|х=х0 = y 0, y'|х=x 0 = y'0 y// + a(x)y/ + b(x)y = 0 y 1(x) и у2(х): y = C 1 y 1 + C 2 y 2 y// + a(x)y/ + b(x)y = f(x) u(х, у, z):

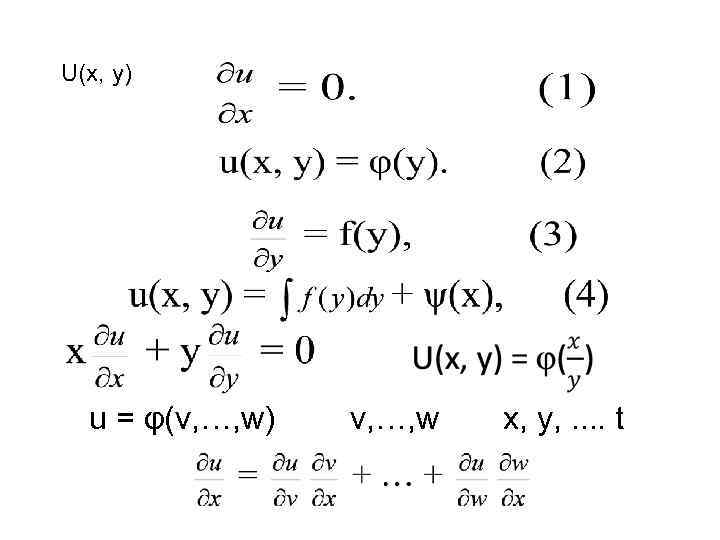U(x, y) u = φ(v, …, w) v, …, w х, у, . . t

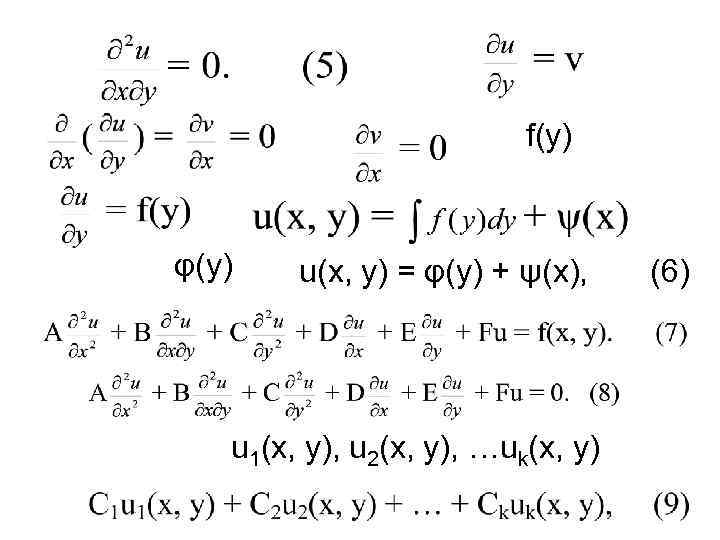f(у) φ(у) u(x, y) = φ(у) + ψ(x), u 1(х, у), u 2(x, y), …uk(x, y) (6)

u 1(х, у), u 2(х, y), …un(x, y) u(х, у, λ) (λ 0, λ 1) Оператор Лапласа в полярных, цилиндрических и сферических координатах. u(х, у, z) u(х, у) x = r cos φ, y = r sin φ. (3)

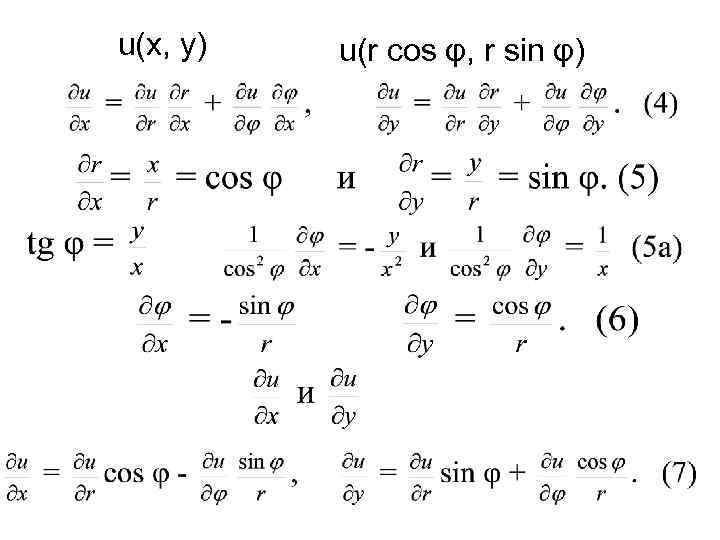u(х, у) u(r cos φ, r sin φ)

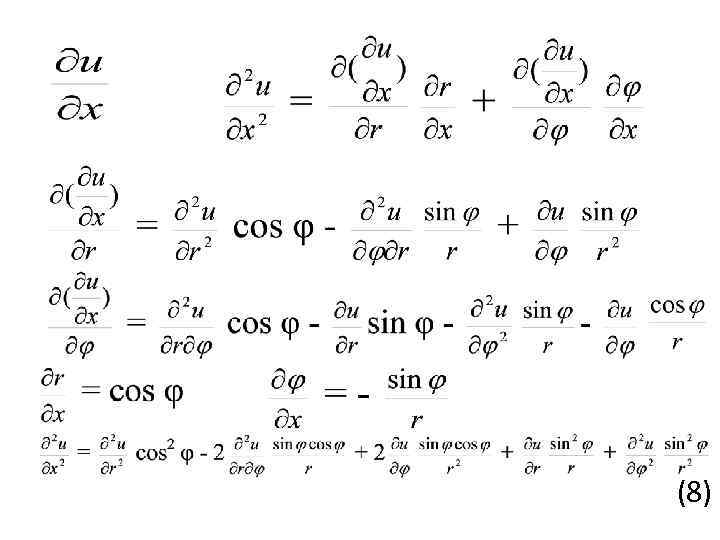(8)

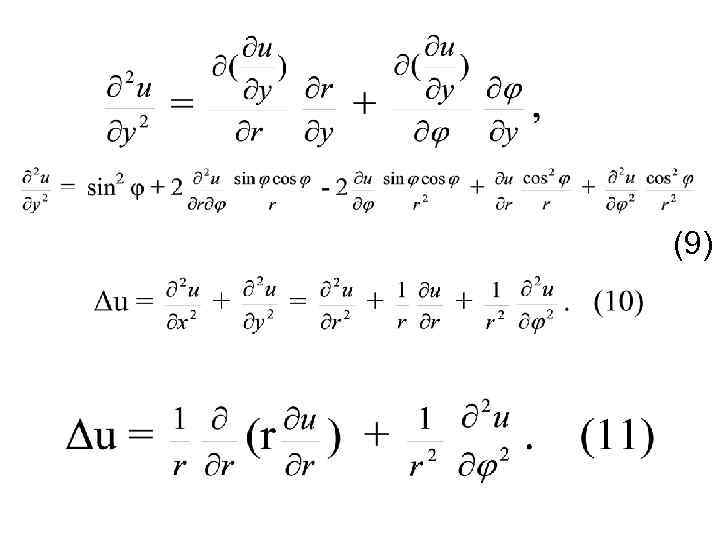(9)

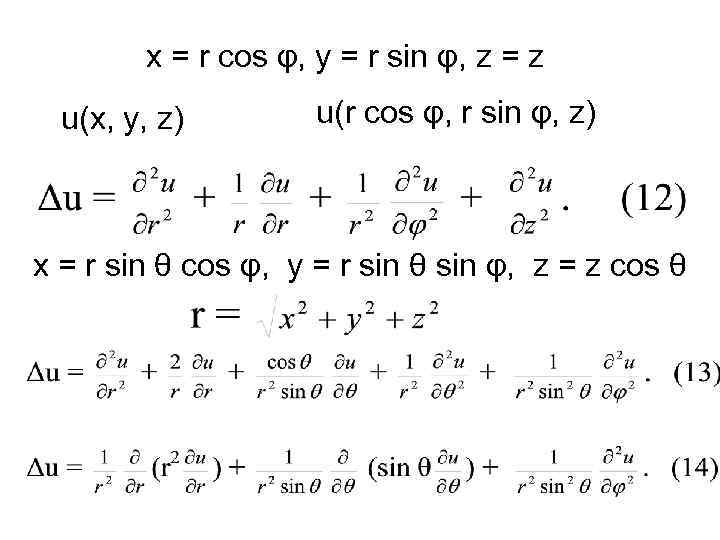x = r cos φ, y = r sin φ, z = z u(х, у, z) u(r cos φ, r sin φ, z) x = r sin θ cos φ, y = r sin θ sin φ, z = z cos θ

Ряды Фурье у = sin x, у = cos x, (Т = 2π ) и у = tg x, у = ctg x (Т = π ) у = А·sin(ωt + φ0) Т= у = Asin(ωt + φ0) = Asin φ0 cos ωt + Acos φ0 sin ωt (4. 1) a = Asin φ0, b = Acos φ0 у = acos ωt + bsin ωt cos ωt и sin ωt (4. 2) φ(t) = А 0 + А 1 sin(t + φ1) + А 2 sin(2 t + φ2) +. . . + А 30 sin(30 t + φ30) = = A 0 + An sin(nt + φn) = А 0 + (ancos nt + bnsin nt) (4. 3)

Т 1 = 2π у = Ао Т 2 = φ(t) Т 3 = Т 30 = 2π + а 1 cos x + b 1 sin x +. . . + ancos nx + bnsin nx +. . . или + ancos nx + bnsin nx , (4. 4) а 0, аn, bn (n = 1, 2, . . . ) (4. 6)

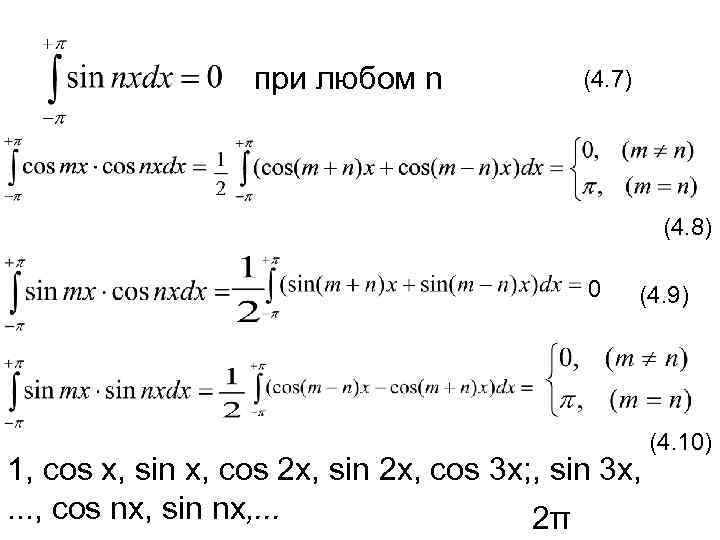при любом n (4. 7) (4. 8) 0 (4. 9) 1, cos x, sin х, cos 2 x, sin 2 x, cos 3 x; , sin 3 x, . . . , cos nx, sin nx, . . . 2π (4. 10)

[0; 2π] Пусть f(x) 2π f [-π; π] а 0, аn bn

соs mx от -π до +π m=n sin mx [-π; π]

[-π; π] f(x) ~ S(x) 2π – периодические f(x) Теорема Дирихле [-π; π] условия Дирихле S(x) = f(x) х = -π и х = π