МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ Модель Объект Алгоритм Программа

МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Модель Объект Алгоритм Программа

Обыкновенные дифференциальные уравнения и задача Коши T, C 100 Задача Температура хлеба вынутого из печи падает от 100 до 60 С за 20 мин. Температура окружающего воздуха 25 С. Через какое время температура хлеба понизится до 30 С? 60 30 25 t, мин 0 20 t = ? Решение Скорость охлаждения тела выражается производной По закону Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Этот процесс неравномерный. С изменением разности температур меняется и скорость охлаждения тела.

Уравнение которое описывает дифференциальное уравнение: данный процесс есть обыкновенное - температура хлеба - температура окружающего воздуха - коэффициент пропорциональности - скорость охлаждения хлеба Учитывая дополнительные условия получаем следующую задачу Коши

Решая задачу Коши получаем неизвестную функцию остывания хлеба 100 T ( t) 50 следовательно при t 0 50 100 При решении данной задачи мы рассматривали батон хлеба, как точку которая остывает равномерно по объёму. Однако хорошо известно, что внутри тела температура понижается медленнее чем на краях. Таким образом если мы хотим моделировать процесс остывания, то будем иметь дело с функцией .

Методы математической физики применяются для изучения математических моделей физических явлений, связанных с различными физическими полями и волновыми процессами в теории упругости, гидрои аэродинамике, электродинамике, акустике и ряде других направлений исследования физических явлений в сплошных средах.

Математические модели этого класса явлений, как правило, описываются при помощи дифференциальных уравнений в частных производных (ДУЧП).

Рассматриваются: основные типы дифференциальных уравнений в частных производных; постановки задач для уравнений в частных производных; классические методы решения уравнений в частных производных; основные сведения о численных методах решения задач математической физики.

Большинство физических законов формулируются на языке уравнений с частными производными. Так, в основе электродинамики лежат уравнения Максвелла, в квантовой механике – уравнение Шредингера, уравнения Навье-Стокса – в гидродинамике.

При рассмотрении функций зависящих от двух и более переменных, приходится работать с частными производными В таком случае процесс распространения тепла будет описываться не обыкновенным дифференциальным уравнением, а уравнением в частных производных.

Основные уравнения математической физики

Уравнение теплопроводности описывает процессы распространения тепла в однородном изотропном теле, процессы диффузии. - коэффициент температуропроводности

Волновое уравнение позволяет изучать упругие, звуковые, электромагнитные волны и другие колебательные явления. - скорость распространения волны в данной среде.

Уравнение Пуассона рассматривает установившееся тепловое состояние в однородном изотропном теле

Уравнение Лапласа описывает установившееся тепловое состояние в однородном изотропном теле

КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Порядок уравнения (наибольший порядок частных производных, входящих в уравнение) уравнение 1 -го порядка уравнение 2 -го порядка

Число независимых переменных 2 независимые переменные: x, y 4 независимые переменные: x, y, z , t

Линейность В линейных уравнениях неизвестная функция и ее частные производные не могут умножаться друг на друга, возводиться в степень. линейное уравнение нелинейное уравнение

Наличие производной по времени стационарное уравнение нестационарное уравнение

Линейные уравнения второго порядка с постоянными коэффициентами а) , параболический тип б) , гиперболический тип в) , эллиптический тип

Начальные и граничные условия

НАЧАЛЬНЫЕ УСЛОВИЯ Определяют значения искомой функции или ее частные производные во всем рассматриваемом объёме, в начальный момент времени. В уравнении присутствует первая производная по времени

В уравнении присутствует вторая производная по времени

Если в уравнении отсутствуют производные по времени, то процесс стационарный, т. е. не зависит от времени. В этом случае начальные условия не используются.

ГРАНИЧНЫЕ УСЛОВИЯ Определяют значения искомой функции или ее частных производных на границе рассматриваемой области в любой момент времени.

Г У 1 -го рода На границе области задают значения искомой функции:

Г У 2 -го рода На границе области задают значения нормальной производной искомой функции:

Г У 3 -го рода На границе области задают линейную комбинацию искомой функции и ее производной по нормали к границе

Кроме начальных и граничных условий к условиям однозначности относятся : физические условия определяемые как правило из эксперимента, например для уравнения теплопроводности необходимо задать коэффициент температуропроводности, для волнового уравнения скорость распространения волны. геометрические условия - размеры и уравнения области, в которой ищется решение задачи.

Математическая задача, является корректно поставленной если: решение существует решение единственно решение устойчиво

МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Аналитические методы Позволяют находить решение уравнения в виде формул. метод разделения переменных, метод интегральных преобразований, и др.

Численные методы Позволяют получать приближенное решение, методом итераций. Подавляющее большинство всех современных инженерных расчетов производятся с использованием приближенных или численных методов. Их широкое использование стало возможным благодаря развитию высокопроизводительных ЭВМ, способных хранить в памяти большие массивы данных и производить над ними арифметические действия с большой скоростью.

Численные методы Позволяют получать приближенное решение, методом итераций.

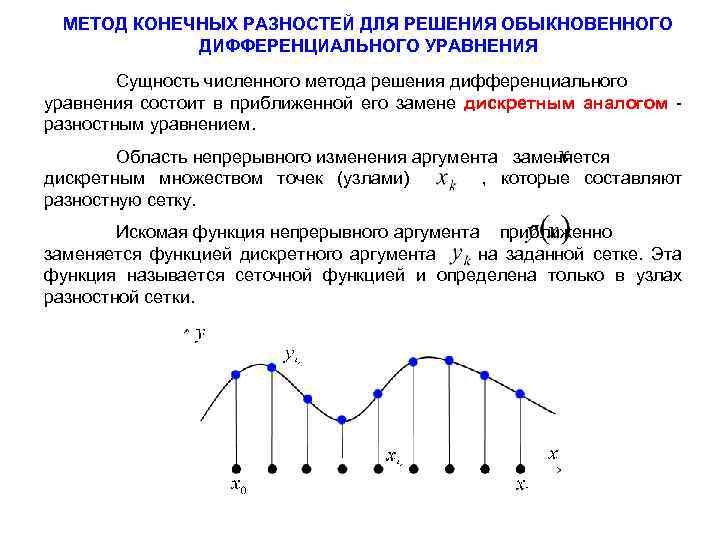
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ РЕШЕНИЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Сущность численного метода решения дифференциального уравнения состоит в приближенной его замене дискретным аналогом разностным уравнением. Область непрерывного изменения аргумента заменяется дискретным множеством точек (узлами) , которые составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной функцией и определена только в узлах разностной сетки.

Для получения разностного аналога для производной первого порядка привлекают определение производной (1) Так как в ЭВМ невозможно осуществить операцию нахождения предела отношения бесконечно малых чисел, то точное соотношение (1) заменяют приближенным: (2) формула правых разностей Если вместо взять , то формула примет вид: (3) формула левых разностей

Из формул (2) и (3) легко получить: (4) формула центральных разностей Разностный аналог для производной второго порядка: (5) формула центральных разностей

Какова степень приближения полученных формул? Рассмотрим формулу правых разностей. Разложим функцию в ряд Тейлора в окрестности точки погрешность главный член погрешности порядок аппроксимации

1 -й порядок аппроксимации формула правых разностей формула левых разностей 2 -й порядок аппроксимации формулы центральных разностей

Пример. Требуется найти численное решение задачи Коши на отрезке Решение. Разобьем область изменения аргумента на отрезков длиной - количество отрезков - шаг разностной сетки - координаты узлов

В качестве каждой точки выберем шаг разностной сетки , тогда уравнение для запишется в виде : Так как полученное уравнение есть приближение уравнения, то результатом его решения будет не точное значение функции , а приближенное, которое обозначим как.

Выразим через где (5) Множество уравнений (5) есть система алгебраических уравнений, которая вместе с начальным условием образуют разностную схему для дифференциального уравнения.

Получим решение данной системы

Пусть Тогда y 1 0. 5 0 2 Численное решение задачи Коши. x

Решим задачу аналитическим методом (метод разделения переменных). Общее решение Используем начальное условие

Сравним аналитическое и численное решения на отрезке y 1 y (x ) = e , -x x = 2, y ( 2) = e. -2 0. 5 0 2 x

Однако не всякая разностная схема дает удовлетворительное решение. К разностной схеме предъявляют требования относительно их аппроксимации, устойчивости и сходимости. ПОГРЕШНОСТЬЮ АППРОКСИМАЦИИ (погрешностью приближения) называют разность между дифференциальным уравнением и его разностным аналогом. Разностная схема называется УСТОЙЧИВОЙ, если на каждом шаге вычислений любая ошибка (погрешность аппроксимации, погрешность округления и т. д. ) не возрастает при переходе от одного шага к другому. Если обозначить через разность между значением сеточной функции и искомой функции в точке , то говорят, что разностная схема СХОДИТСЯ, если при , т. е. решение разностной задачи сходится к решению дифференциальной задачи.

теорема Лакса Если имеется корректно поставленная линейная задача с начальными условиями, и конечно-разностная схема аппроксимирует исходное дифференциальное уравнение, то устойчивость является необходимым и достаточным условием сходимости АППРОКСИМАЦИЯ + УСТОЙЧИВОСТЬ = СХОДИМОСТЬ

РЕШЕНИЕ УРАВНЕНИЯ ЛАПЛАСА МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ a a с 9 с d 10 b a b c d = = 1. 0 1. 5 2. 5 0. 2

ЗАПИСЬ ГРАНИЧНЫХ УСЛОВИЙ 5 -я стенка 1 -го рода 2 -го рода 6 -я стенка 2 -го рода 1 -го рода 7 -я стенка 3 -я стенка 2 -го рода 1 -го рода 8 -я стенка 4 -я стенка 2 -го рода 1 -го рода

ПОСТРОЕНИЕ РАСЧЁТНОЙ СЕТКИ Сетка размером Mi x Mj, dx=(a+c)/(Mi-1) dy=(a+b)/(Mj-1) Mi=41, (Mi-1, Mj-1) (0, Mj-1) a (Mi 1, Mj-1) Mj=41 a (Mi 1, Mj 1) (Mi 2, Mj 3) (Mi 2, Mj 2) (0, 0) с (Mi-1, Mj 1) (Mi 3, Mj 3) b (Mi 3, Mj 2) (Mi-1, 0) Mi 1=a/dx Mj 1=b/dy Mi 2=a/2/dx Mi 3=(a/2+c)/dx Mj 2=(b/2 -d/2)/dy Mj 3=(b/2+d/2)/dy

2 -я стенка for (i=0; i<=Mi 1; i++) { T[i][Mj-1]=100; } 1 -я стенка for (j=0; j<=Mj-1; j++) { T[0][j]=T[1][j]; } (0, Mj-1) (Mi 1, Mj 1) (Mi-1, Mj-1) (Mi-1, Mj 1) (Mi 3, Mj 2+1) (Mi 2, Mj 2) (0, 0) (Mi 2, Mj 2+1) (Mi 3, Mj 2) (Mi-1, 0)

3 -я стенка for (j=Mj 1; j<=Mj-1; j++) { T[Mi 1][j]=T[Mi 1 -1][j]; } (0, Mj-1) (Mi 1, Mj 1) (Mi-1, Mj-1) (Mi 1, Mj-1) 4 -я стенка for (i=Mi 1; i<=Mi-1; i++) { T[i][Mj 1]=T[i][Mj 1 -1]; } (Mi-1, Mj 1) (Mi 3, Mj 2+1) (Mi 2, Mj 2) (0, 0) (Mi 2, Mj 2+1) (Mi 3, Mj 2) (Mi-1, 0)

6 -я стенка for (i=0; i<=Mi-1; i++) { T[i][0]=T[i][1]; } 5 -я стенка for (j=0; j<=Mj 1; j++) { T[Mi-1][j]=100; } (0, Mj-1) (Mi 1, Mj 1) (Mi-1, Mj-1) (Mi-1, Mj 1) (Mi 3, Mj 2+1) (Mi 2, Mj 2) (0, 0) (Mi 2, Mj 2+1) (Mi 3, Mj 2) (Mi-1, 0)

8 -я стенка for (i=Mi 2; i<=Mi 3; i++) { T[i][Mj 2+1]=0; } 7 -я стенка for (i=Mi 2; i<=Mi 3; i++) { T[i][Mj 2]=0; // 7 -я } (0, Mj-1) (Mi 1, Mj 1) (Mi-1, Mj-1) (Mi-1, Mj 1) (Mi 3, Mj 2+1) (Mi 2, Mj 2) (0, 0) (Mi 2, Mj 2+1) (Mi 3, Mj 2) (Mi-1, 0)

Заменим частные производные разностными аналогами, используя разностную схему «крест» . i, j+1 i, j i-1, j i+1, j i, j-1 i=1, Mi-2 j=1, Mj-2

(0, 3) (1, 3) (2, 3) (3, 3) (0, 2) (1, 2) (2, 2) (3, 2) (0, 1) (1, 1) (2, 1) (3, 1) (0, 0) (1, 0) (2, 0) (3, 0) i=1 j=1

Получили систему линейных алгебраических уравнений: Таким образом, уравнение в частных производных заменяется на систему линейных алгебраических уравнений.

Для решения системы линейных уравнений применим итерационный метод Гаусса-Зейделя. i=1, Mi-2 j=1, Mj-2 Для увеличения скорости сходимости итерационного процесса воспользуемся методом верхней релаксации. i=1, Mi-2 j=1, Mj-2

Если i=1, Mi-2 и j=1, Mj-2, то область изменения i и j – прямоугольник. В нашем случае имеется выступ и стержень с постоянной температурой. Запишем условие обхода: (0, Mj-1) (Mi 1, Mj-1) (Mi-1, Mj-1) Mi 1<i<Mi-1 (Mi 1, Mj 1) (Mi 2, Mj 2+1) (Mi 2, Mj 2) (0, 0) (Mi-1, Mj 1) (Mi 3, Mj 3) (Mi 3, Mj 2) (Mi-1, 0) Mj 1<j<Mj-1 Mi 2<i<Mi 3 Mj 2<j<Mj 3

АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА построение расчетной сетки (вычисление шагов, узлов) задание Г. У. 1 -го рода расчет уравнения Лапласа во внутренних точках Расчет Г. У. 2 -го рода достигнута сходимость ? Вывод данных в файл, рисование поля температуры

СОСТАВЛЕНИЕ ПРОГРАММЫ НА ЯЗЫКЕ С/С++ #include <conio. h> #include <math. h> #include <stdio. h> int main(void) { int const Mi=80, Mj=80; // размер сетки int Mi 1, Mj 2, Mi 3; // координаты узлов float T[Mi][Mj]={0}, TK, Tzv; a, b, c, dx, dy; // размеры области, шаг сетки relax=1. 5; E=1; // сумарная погрешность float shod; int iter=0; int i, j; // сходимость // текущая итерация // для организации цикла

a=1. 0; b=1. 5; c=0. 5; dx=(a+c)/(Mi-1); //---расчёт шагов dy=(a+b)/(Mj-1); Mi 1=a/dx; //---расчёт узлов Mj 1=b/dy; Mi 2=a/2/dx; Mi 3=(a/2+c)/dx; Mj 2=b/2/dy; printf("Control points. . n"); //проверка узлов printf(" Mi 1=%d n Mi 2=%d n Mi 3=%d n", Mi 1, Mi 2, Mi 3); printf(" Mj 1=%d n Mj 2=%d n", Mj 1, Mj 2); getch(); //====== Граничные for (i=0; i<=Mi 1; i++) for (j=0; j<=Mj 1; j++) for (i=0; i<=Mi-1; i++) for (i=Mi 2; i<=Mi 3; i++) условия 1 рода===== T[i][Mj-1]=100; // 2 стенка T[Mi-1][j]=100; // 5 стенка T[i][0]=0; // 6 стенка T[i][Mj 2]=0; // 7 стенка T[i][Mj 2+1]=0; // 8 стенка

//======Расчёт во внутренних точках======= do { shod=0. 0; for(i=1; i<=Mi-2; i++) { for(j=1; j<=Mj-2; j++) { if ((i>=Mi 1)&&(j>=Mj 1) || (i>=Mi 2)&&(i<=Mi 3) && (j>=Mj 2)&&(j<=Mj 2+1)) continue; TK=T[i][j]; Tzv=((T[i+1][j]+T[i-1][j])/(dx*dx)+ (T[i][j+1]+T[i][j-1])/(dy*dy))/ (2/(dx*dx)+2/(dy*dy)); T[i][j]=Tzv*relax+TK*(1 -relax); //вычисление суммарной погрешности shod=shod+fabs(TK-T[i][j]); } }

//====Граничные условия 2 рода======= for (j=0; j<=Mj-1; j++) T[0][j]=T[1][j]; // 1 for (j=Mj 1; j<=Mj-1; j++) T[Mi 1][j]=T[Mi 1 -1][j]; // 3 for (i=Mi 1; i<=Mi-1; i++) T[i][Mj 1]=T[i][Mj 1 -1]; // 4 printf("n shod = %f } while(shod>E); iter=%d", shod, iter++); //======вывод в файл====== FILE *fp; // ----- открываем файл if ((fp=fopen("C: \teplo. txt", "w"))!=NULL) { // ---- записываем данные fprintf(fp, "%dt%dn", Mi, Mj); for(i=0; i<=Mi-1; i++) { for(j=0; j<=Mj-1; j++) {

if ((i>=Mi 1)&&(j>=Mj 1)|| (i>=Mi 2)&&(i<=Mi 3)&& (j>=Mj 2)&&(j<=Mj 2+1)) continue; fprintf(fp, "%dt%fn", i, j, T[i][j]); } } fclose(fp); // ------ закрываем файл printf("nnn. Data is Ok!"); getch(); } else printf("nnn. Error while creating file. . "); getch(); return 0; }