Скачать презентацию МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЛЕКЦИЯ 10 НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ Скачать презентацию МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЛЕКЦИЯ 10 НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ

Презентация 8_простейшие ММ_Q схемы.ppt

  • Количество слайдов: 92

МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЛЕКЦИЯ № 10 «НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Q-СХЕМЫ)» 1 МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЛЕКЦИЯ № 10 «НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Q-СХЕМЫ)» 1

Модель –- объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала. » (Советов Б. Я. , Модель –- объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала. » (Советов Б. Я. , Яковлев С. А. ) Математическая модель - математическое представление реальности Алексей Андреевич Ляпунов 1911 -1973 2 Моделирование (по А. А. Ляпунову)- опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель): - находящаяся в некотором объективном соответствии с познаваемым объектом; - способная замещать его в определенных отношениях; - дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте

Система - целостное множество взаимосвязанных элементов, которое нельзя расчленить на независимые подмножества. «Правильно заданный Система - целостное множество взаимосвязанных элементов, которое нельзя расчленить на независимые подмножества. «Правильно заданный вопрос — половина ответа» модели массового обслуживания (ММО) - математические объекты, описываемые в терминах соответствующего математического аппарата. базовые модели в виде систем массового обслуживания 3 сетевые модели в виде сетей массового обслуживания,

Агнер Краруп Эрланг 4 Агнер Краруп Эрланг 4

Системы массового обслуживания (СМО) - системы специального вида, реализующие многократное выполнение однотипных задач. 5 Системы массового обслуживания (СМО) - системы специального вида, реализующие многократное выполнение однотипных задач. 5

Задача: Какое количество телефонисток (при условии их полной занятости) должно работать на станции для Задача: Какое количество телефонисток (при условии их полной занятости) должно работать на станции для того, чтобы потери требований были минимальными. Задача: Определить количество врачей, вспомогательного персонала, автомашин, для того чтобы время ожидания вызова было для больных оптимальным при условии минимизации затрат на эксплуатацию системы и максимизации качества обслуживания. 6 Задача: Обеспечить определенный объем перевозок при минимальных расходах. При этом сократить простои судов при погрузочно-разгрузочных работах. Задача: Обеспечить ускорение обработки сигналов при заданной суммарной длине очереди.

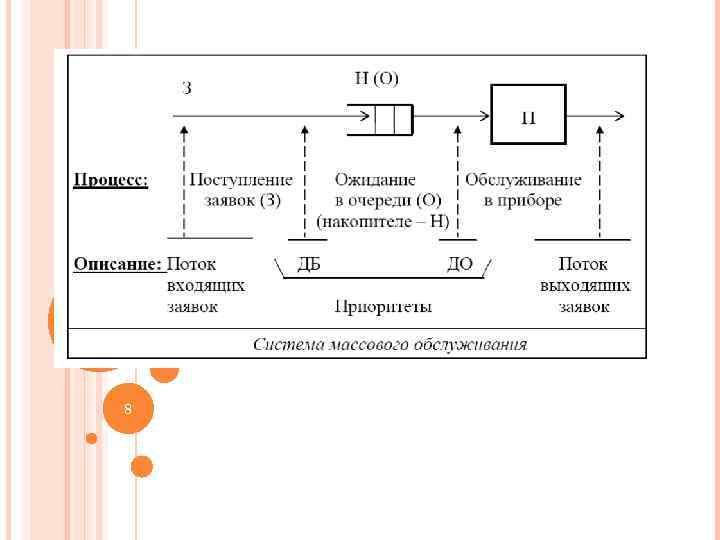
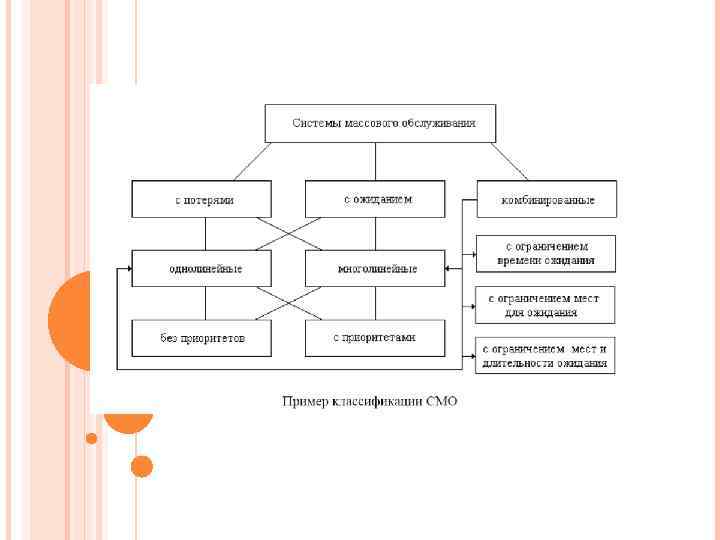
Системы с ожиданием – заявка, поступившая на вход системы “ждет” очереди на выполнение Системы Системы с ожиданием – заявка, поступившая на вход системы “ждет” очереди на выполнение Системы с потерями– заявка из-за занятости канала обслуживания получает отказ и теряется для СМО. üтребования на обслуживание принимаются до тех пор, пока очередь не достигнет заданного размера; üтребования остаются в очереди, но ожидают обслуживания не более заданного времени, после чего из очереди исключаются; üвремя ожидания обслуживания и время самого обслуживания ограничивается некоторой величиной 7

8 8

9 9

10 10

11 11 11 11

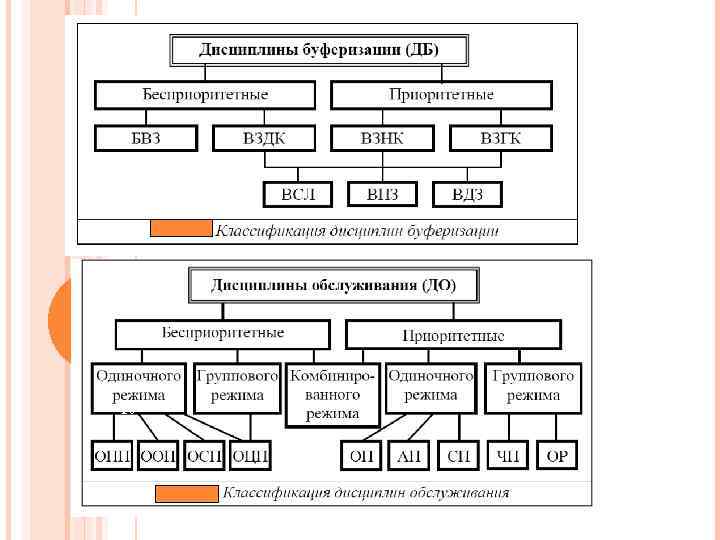
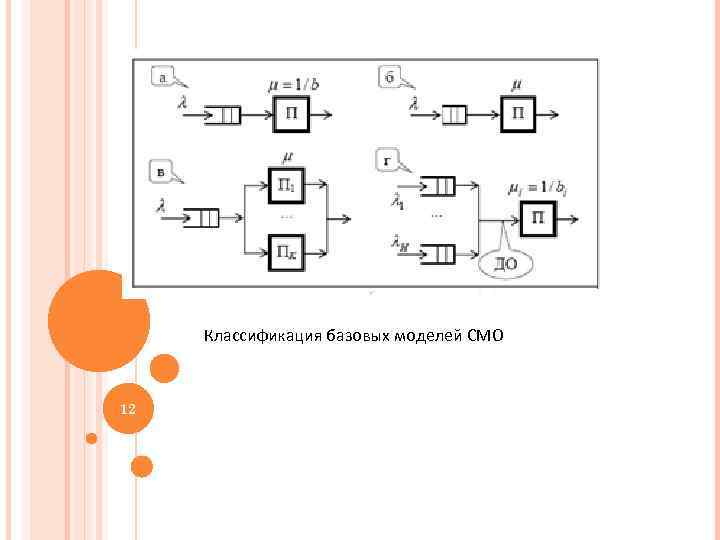Классификация базовых моделей СМО 12 12 Классификация базовых моделей СМО 12 12

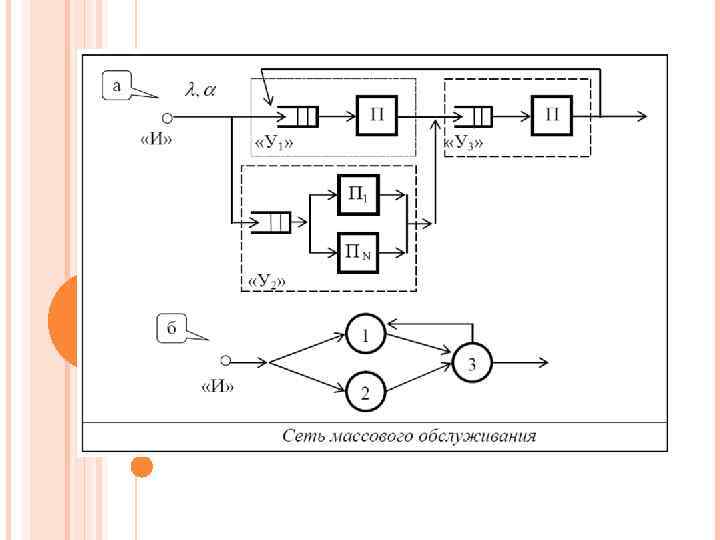
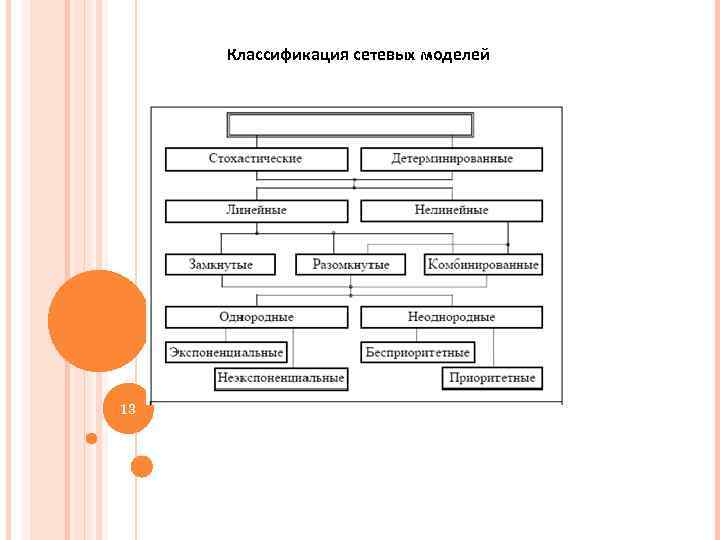Классификация сетевых моделей 13 13 Классификация сетевых моделей 13 13

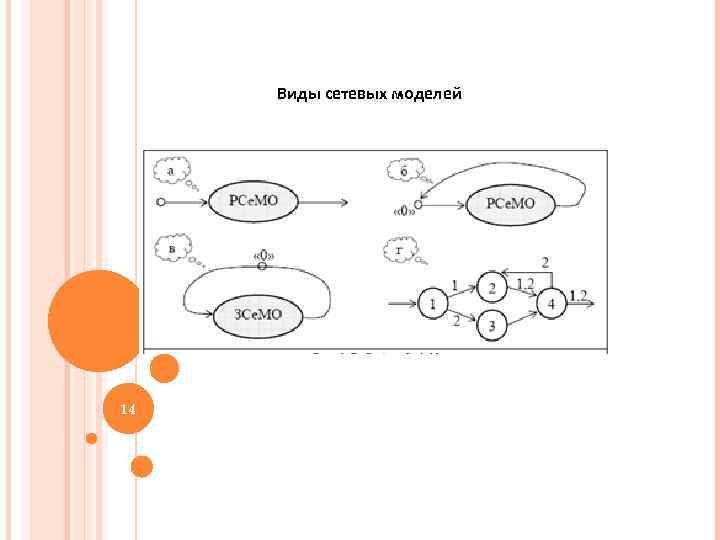Виды сетевых моделей 14 14 Виды сетевых моделей 14 14

«МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТОКОВ СОБЫТИЙ» 15 1. 2. 3. 4. 5. Поток заявок Свойства «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТОКОВ СОБЫТИЙ» 15 1. 2. 3. 4. 5. Поток заявок Свойства простейшего пуассоновского потока Длительность обслуживания заявок Стратегии управления потоками заявок Простейший поток и решение практических задач.

1. Вероятность – численная мера степени объективной возможности некоторого события. Вероятность может принимать только 1. Вероятность – численная мера степени объективной возможности некоторого события. Вероятность может принимать только положительные значения из интервала [0; 1]. Величина, принимающая значение, неизвестное заранее, называется случайной. Различают дискретные (прерывные) и непрерывные (аналоговые) случайные величины. 2. Закон распределения случайной величины – соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения дискретной случайной величины может быть задан: · аналитически в виде математического выражения; · таблично в виде ряда распределения; · графически в виде многоугольника распределения. Закон распределения непрерывной случайной величины может быть задан в виде: · функции распределения F(x) случайной величины X, представляю16 щей собой вероятность того, что случайная величина X примет значение меньшее, чем некоторое заданное значение x: F(x) = P(X < x); · плотности распределения f(x), определяемой как производная от функции распределения F(x) по x: f (x) = F¢(x).

Функция распределения однозначно определяется через плотность распределения как Свойства функции распределения: · F(x) – Функция распределения однозначно определяется через плотность распределения как Свойства функции распределения: · F(x) – неубывающая функция: ------ · функция распределения принимает значения от 0 до 1 , причём: Свойства плотности распределения: · плотность распределения принимает только неотрицательные значения: · площадь на графике, ограниченная плотностью распределения и осью абсцисс, всегда равна единице: 17 3. Числовые характеристики – начальные и центральные моменты – позволяют выразить в сжатой форме наиболее существенные особенности распределения случайной величины

4. В моделях дискретных систем наиболее широко применяются следующие законы распределений случайных величин: · 4. В моделях дискретных систем наиболее широко применяются следующие законы распределений случайных величин: · распределение Пуассона (дискретный закон): ------ где a – параметр распределения (a > 0); · геометрическое распределение (дискретный закон): где r – параметр распределения (0 < r <1); · равномерное распределение (непрерывный закон) с плотностью 18 · экспоненциальное распределение (непрерывный закон) с функцией и плотностью где a > 0 - параметр распределения;

· распределение Эрланга k-го порядка (непрерывный закон) с функцией и плотностью: ------ математическое ожидание · распределение Эрланга k-го порядка (непрерывный закон) с функцией и плотностью: ------ математическое ожидание распределения Эрланга зависит от значения параметра k; · нормированное распределение Эрланга (непрерывный закон) с функцией и плотностью: 19 коэффициент вариации нормированного распределения Эрланга также меньше или равен единице: но математическое ожидание не зависит от значения параметра k;

· гиперэкспоненциальное распределение (непрерывный закон): ------ · гиперэрланговское распределение представляет собой аддитивную смесь нормированных · гиперэкспоненциальное распределение (непрерывный закон): ------ · гиперэрланговское распределение представляет собой аддитивную смесь нормированных распределений Эрланга и является наиболее общим распределением неотрицательных непрерывных случайных величин, поскольку имеет коэффициент вариации в интервале от 0 до плотность гиперэкспоненциального распределения: 20

«Цепь Маркова с конечным числом состояний и дискретным временем» 21 «Цепь Маркова с конечным числом состояний и дискретным временем» 21

1. Понятие случайного процесса. Случайный процесс находится в некотором состоянии, если он полностью описывается 1. Понятие случайного процесса. Случайный процесс находится в некотором состоянии, если он полностью описывается значениями переменных, которые задают это состояние S Процесс совершает переход из одного состояния в другое, если описывающие ее переменные изменяются от значений, задающих одно состояние, на значения, которые определяют другое состояние. Если множество состояний, в которых может находиться процесс счётное, то есть все возможные состояния могут быть пронумерованы, то 22 соответствующий процесс называется случайным процессом с дискретными состояниями или просто дискретным случайным процессом. Если множество состояний не может быть пронумеровано, то имеем случайный процесс с непрерывными состояниями или просто непрерывный случайный процесс, для которого характерен плавный переход из состояния в состояние и который 22 задаётся в виде непрерывной функции времени:

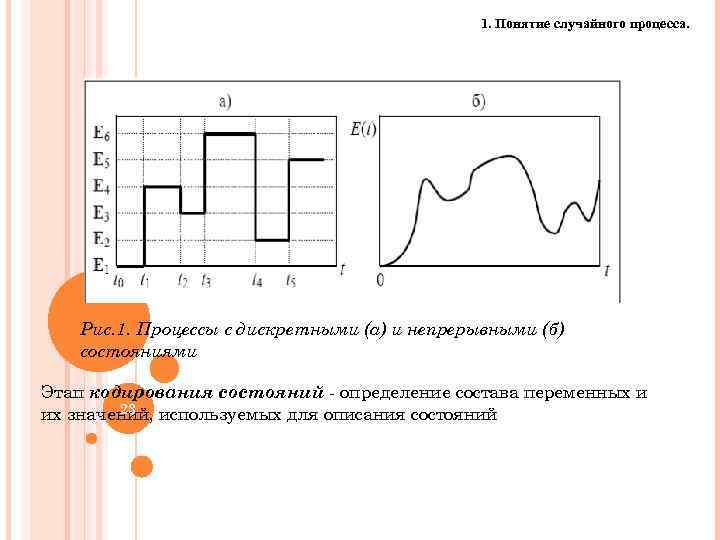1. Понятие случайного процесса. Рис. 1. Процессы с дискретными (а) и непрерывными (б) состояниями 1. Понятие случайного процесса. Рис. 1. Процессы с дискретными (а) и непрерывными (б) состояниями Этап кодирования состояний - определение состава переменных и 23 их значений, используемых для описания состояний 23

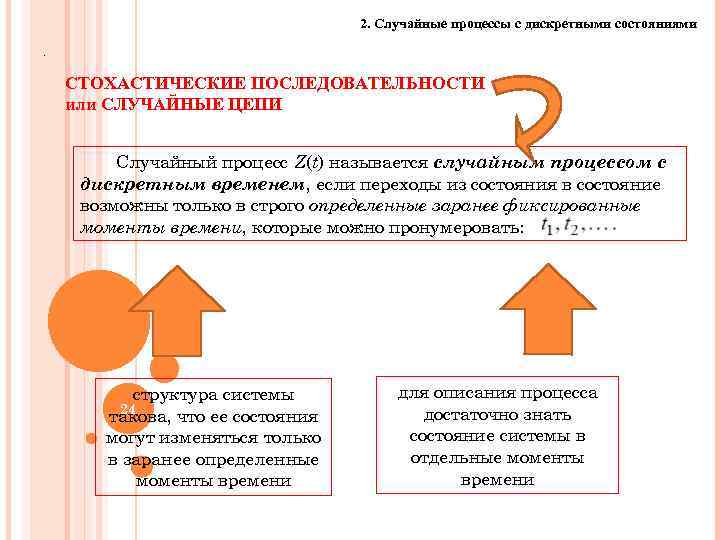2. Случайные процессы с дискретными состояниями. СТОХАСТИЧЕСКИЕ ПОСЛЕДОВАТЕЛЬНОСТИ или СЛУЧАЙНЫЕ ЦЕПИ Случайный процесс Z(t) 2. Случайные процессы с дискретными состояниями. СТОХАСТИЧЕСКИЕ ПОСЛЕДОВАТЕЛЬНОСТИ или СЛУЧАЙНЫЕ ЦЕПИ Случайный процесс Z(t) называется случайным процессом с дискретным временем, если переходы из состояния в состояние возможны только в строго определенные заранее фиксированные моменты времени, которые можно пронумеровать: структура системы 24 такова, что ее состояния могут изменяться только в заранее определенные моменты времени для описания процесса достаточно знать состояние системы в отдельные моменты времени 24

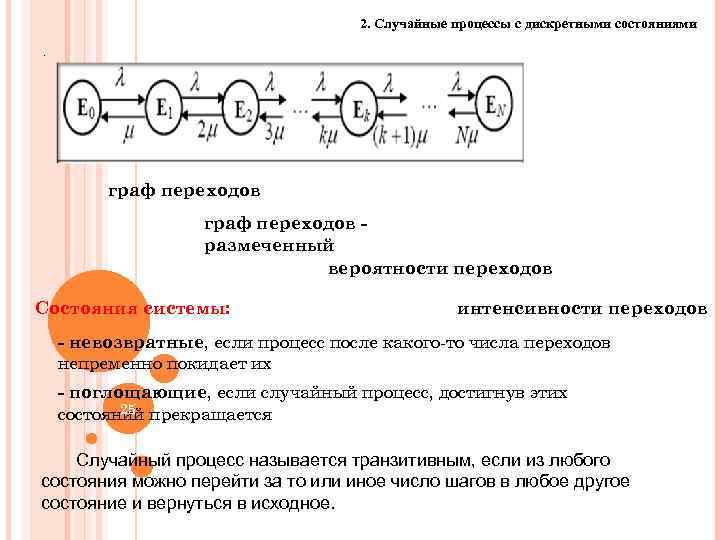2. Случайные процессы с дискретными состояниями. граф переходов размеченный вероятности переходов Состояния системы: интенсивности 2. Случайные процессы с дискретными состояниями. граф переходов размеченный вероятности переходов Состояния системы: интенсивности переходов - невозвратные, если процесс после какого-то числа переходов непременно покидает их - поглощающие, если случайный процесс, достигнув этих 25 состояний прекращается Случайный процесс называется транзитивным, если из любого состояния можно перейти за то или иное число шагов в любое другое состояние и вернуться в исходное. 25

3. Понятие марковского случайного процесса. Параметры и характеристики марковского случайного процесса. Случайный процесс называется 3. Понятие марковского случайного процесса. Параметры и характеристики марковского случайного процесса. Случайный процесс называется марковским, если вероятность любого состояния в будущем зависит только от его состояния в настоящем и не зависит от того, когда и каким образом процесс оказался в этом состоянии 1. Параметры марковского случайного процесса перечень состояний, в которых может находиться случайный процесс; матрица переходов, описывающая переходы случайного процесса между состояниями в виде: матрицы вероятностей переходов Q для процессов с дискретным временем; матрицы интенсивностей переходов G для процессов с непрерывным временем начальные вероятности 26 Цепь Маркова однородная, если неоднородная, если вероятности переходов являются функциями tk , то 26 не зависят от момента есть времени

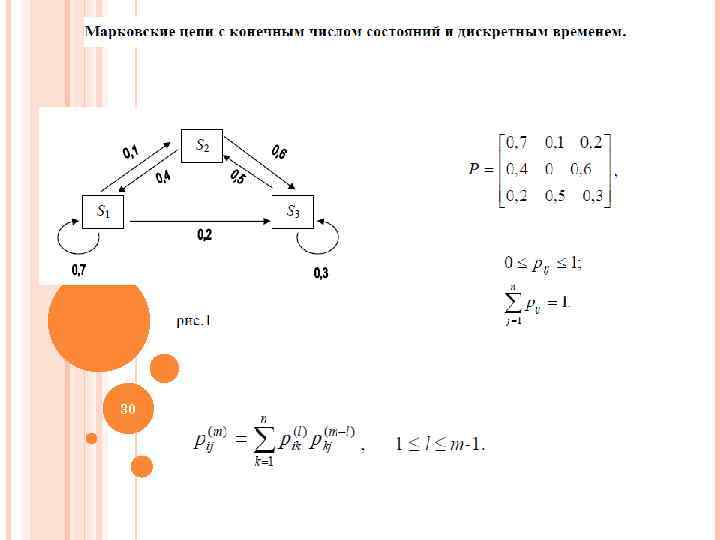
3. Понятие марковского случайного процесса. Параметры и характеристики марковского случайного процесса. МАТРИЦА ВЕРОЯТНОСТЕЙ ПЕРЕХОДОВ 3. Понятие марковского случайного процесса. Параметры и характеристики марковского случайного процесса. МАТРИЦА ВЕРОЯТНОСТЕЙ ПЕРЕХОДОВ стохастическая НАЧАЛЬНЫЕ ВЕРОЯТНОСТИ 27 стационарные характеристики (вероятности) моделируемой системы в установившемся режиме не зависят от начальных вероятностей и, следовательно, могут быть не заданы 27

3. Понятие марковского случайного процесса. Параметры и характеристики марковского случайного процесса. 2. Характеристики марковского 3. Понятие марковского случайного процесса. Параметры и характеристики марковского случайного процесса. 2. Характеристики марковского случайного процесса Нормировочное условие: Вектор с числом координат, равным числу возможных состояний системы 28 Стохастический вектор – вектор состояний 28

4. Эргодическое свойство случайных процессов Если по истечении достаточно большого промежутка времени вероятности состояний 4. Эргодическое свойство случайных процессов Если по истечении достаточно большого промежутка времени вероятности состояний стремятся к предельным значениям не зависящим от начальных вероятностей и от текущего момента времени t , то говорят, что случайный процесс обладает эргодическим свойством. установившийся или стационарный режим 29 неустановившийся режим 29

30 30 30 30

31 31 31 31

Пример. Рассмотрим систему, которая состоит из двух устройств У 1 и У 2, каждое Пример. Рассмотрим систему, которая состоит из двух устройств У 1 и У 2, каждое из которых может находиться в одном из двух состояний: 0 – выключено и 1 – включено. В определённые моменты времени устройства могут включаться или выключаться. Выделим возможные состояния системы: Пусть заданы вероятности переходов в виде матрицы 32 Определим вероятности нахождения системы в том или ином состоянии на различные моменты времени. 32

На момент времени 33 Матрица вероятностей переходов рассматриваемой системы –неразложимая и непериодическая, следовательно, случайный На момент времени 33 Матрица вероятностей переходов рассматриваемой системы –неразложимая и непериодическая, следовательно, случайный процесс обладает эргодическим свойством 33

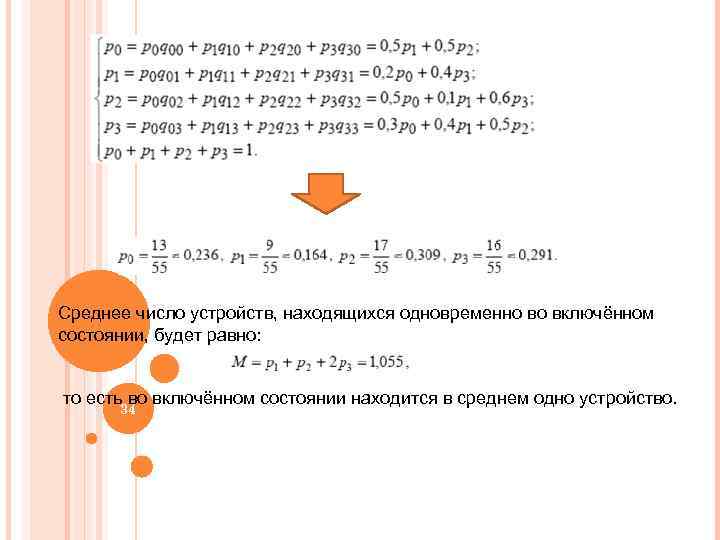Среднее число устройств, находящихся одновременно во включённом состоянии, будет равно: то есть во включённом Среднее число устройств, находящихся одновременно во включённом состоянии, будет равно: то есть во включённом состоянии находится в среднем одно устройство. 34 34

35 35 35 35

36 36 36 36

«Марковские процессы с конечным числом состояний и непрерывным временем» 37 «Марковские процессы с конечным числом состояний и непрерывным временем» 37

Дата рождения: 2 (14) июня 1856 Место рождения: Рязань, Российская империя Дата смерти: 20 Дата рождения: 2 (14) июня 1856 Место рождения: Рязань, Российская империя Дата смерти: 20 июля 1922 (66 лет) Место смерти: Петроград, РСФСР Страна: Российская империя РСФСР Научная сфера: математика Научный руководитель: П. Л. Чебышев Известные ученики: А. С. Безикович, Н. М. Гюнтер, В. Ф. Каган, Я. Д. Тамаркин, Я. В. Успенский, Г. Ф. Вороной Марков Андрей Андреевич С 13 декабря 1886 года — адъюнкт Физико-математического отделения (чистая математика), с 3 марта 1890 года — экстраординарный академик, а 38 с 2 марта 1896 года — ординарный академик Императорской Санкт. Петербургской академии наук. С 1880 года — приват-доцент, с 1886 года — профессор физико-математического факультета Санкт-Петербургского университета. С 1898 года - действительный статский советник.

1. Основные понятия марковских процессов с конечным числом состояний и непрерывным временем Если система 1. Основные понятия марковских процессов с конечным числом состояний и непрерывным временем Если система S может переходить в другое состояние случайным образом в произвольный момент времени, то говорят о случайном процессе с непрерывным временем. В отсутствии последействия такой процесс называется непрерывной марковской цепью. 39 39

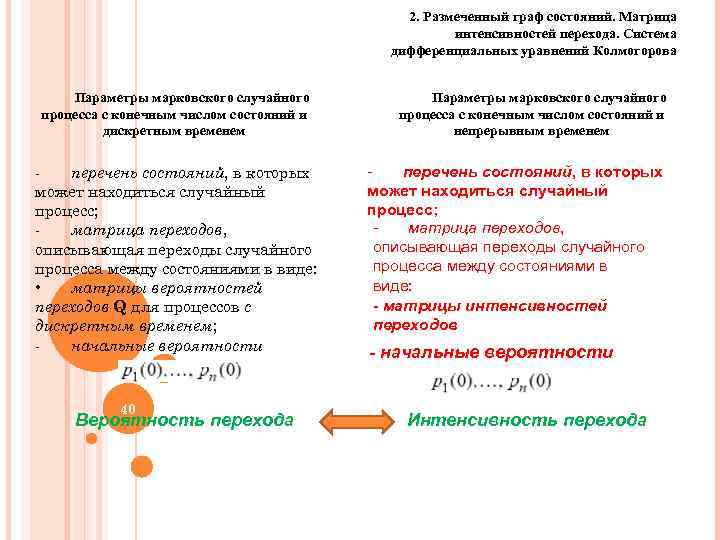2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Параметры марковского случайного 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Параметры марковского случайного процесса с конечным числом состояний и дискретным временем перечень состояний, в которых может находиться случайный процесс; матрица переходов, описывающая переходы случайного процесса между состояниями в виде: • матрицы вероятностей переходов Q для процессов с дискретным временем; начальные вероятности 40 Вероятность перехода Параметры марковского случайного процесса с конечным числом состояний и непрерывным временем перечень состояний, в которых может находиться случайный процесс; матрица переходов, описывающая переходы случайного процесса между состояниями в виде: - матрицы интенсивностей переходов - начальные вероятности Интенсивность перехода 40

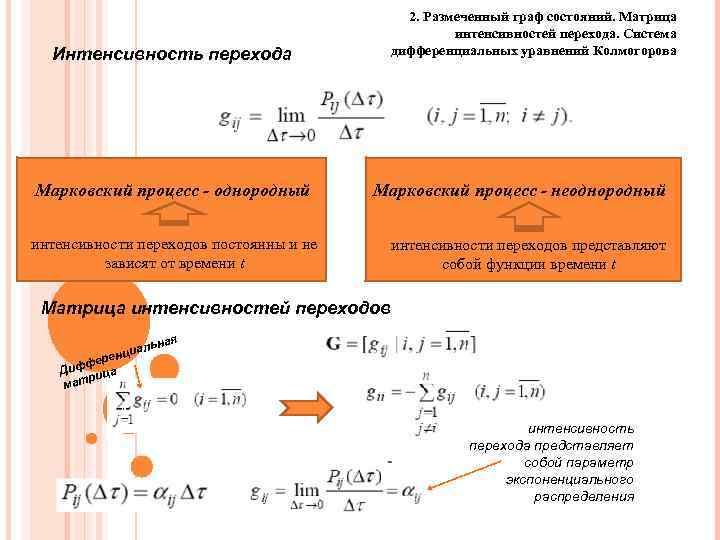2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Интенсивность перехода Марковский 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Интенсивность перехода Марковский процесс - однородный Марковский процесс - неоднородный интенсивности переходов постоянны и не зависят от времени t интенсивности переходов представляют собой функции времени t Матрица интенсивностей переходов ная иаль ренц фе Диф ица р мат 41 интенсивность перехода представляет собой параметр экспоненциального распределения 41

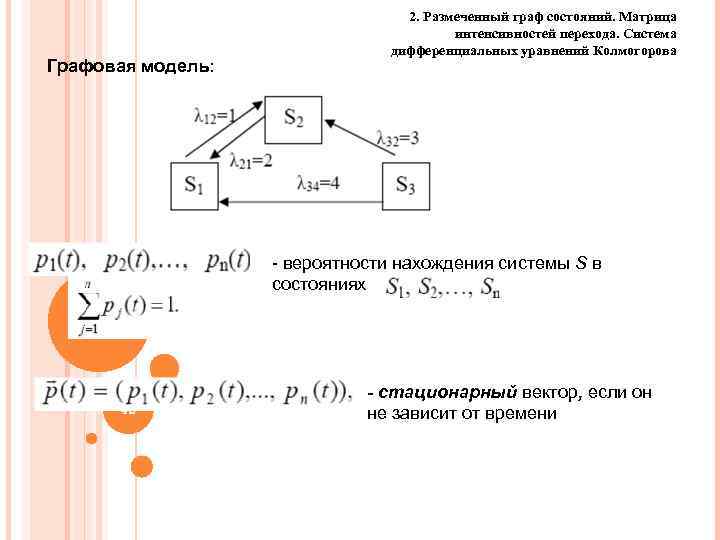Графовая модель: 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова - Графовая модель: 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова - вероятности нахождения системы S в состояниях 42 - стационарный вектор, если он не зависит от времени 42

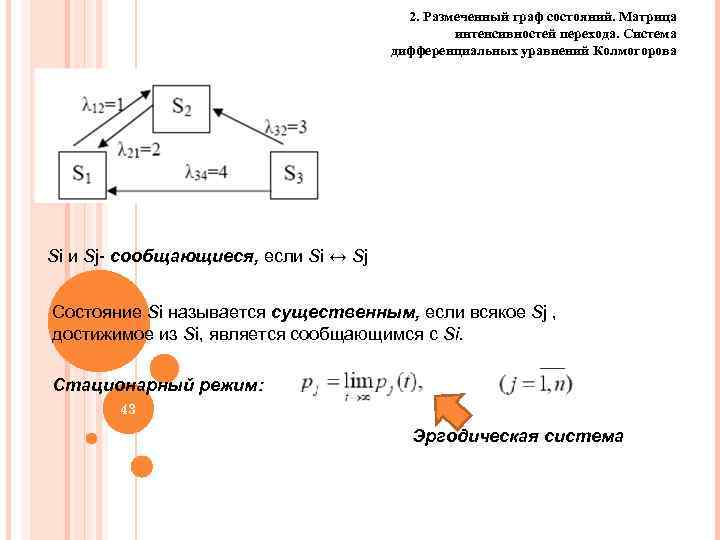2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Si и Sj- 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Si и Sj- сообщающиеся, если Si ↔ Sj Состояние Si называется существенным, если всякое Sj , достижимое из Si, является сообщающимся с Si. Стационарный режим: 43 Эргодическая система 43

2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Пример. Записать уравнения 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Пример. Записать уравнения Колмогорова. Найти финальные вероятности для состояний системы. Общее правило составления уравнений Колмогорова: В левой части каждого из них стоит производная вероятности какого-то (j-го) состояния. В правой части - сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния. 44 44

2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Ответ: вектор состояния 2. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова Ответ: вектор состояния системы в стационарном режиме равен 45 45

«Марковские процессы с конечным числом состояний и непрерывным временем» 46 «Марковские процессы с конечным числом состояний и непрерывным временем» 46

ü Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф ü Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф состояний. ü Условия существования стационарного режима. ü Нахождение предельного распределения вероятностей в случае конечного числа состояний. 47 47

1. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф 1. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф состояний. Биологическая задача об изменении численности популяции и распространении эпидемий Рассмотрим развитие некоторой популяции, особи которой могут рождаться и умирать. Пусть при наличии i особей в популяции -рождение новых особей происходит с интенсивностью i -с интенсивностью i особи умирают. Пусть в любой момент времени может происходить рождение или гибель только одной особи, и интервалы времени между двумя моментами рождения и гибели распределены по экспоненциальному закону с параметрами i и i соответственно. Тогда процесс "гибели и размножения" может быть представлен марковским случайным процессом с непрерывным временем, в 48 котором состояние Еi соответствует наличию i особей в популяции (i=0, 1, …) причем число состояний может быть конечным или бесконечным. 48 нахождение приблизительного количества … в отдельно взятой популяции.

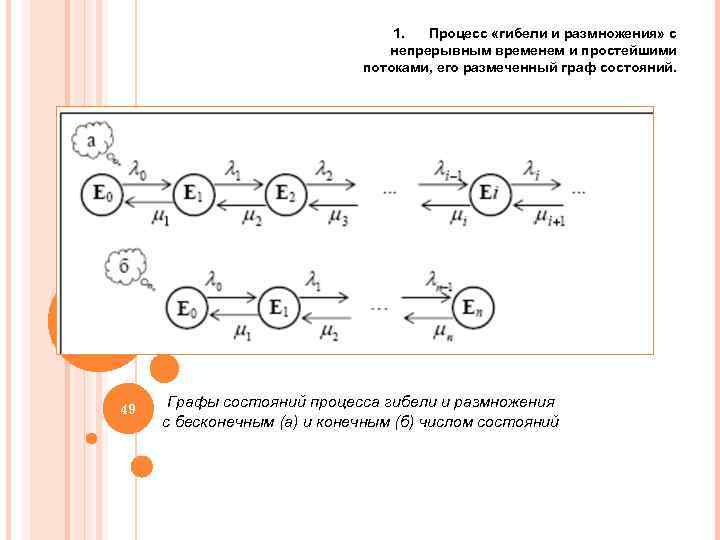1. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф 1. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф состояний. 49 Графы состояний процесса гибели и размножения с бесконечным (а) и конечным (б) числом состояний 49

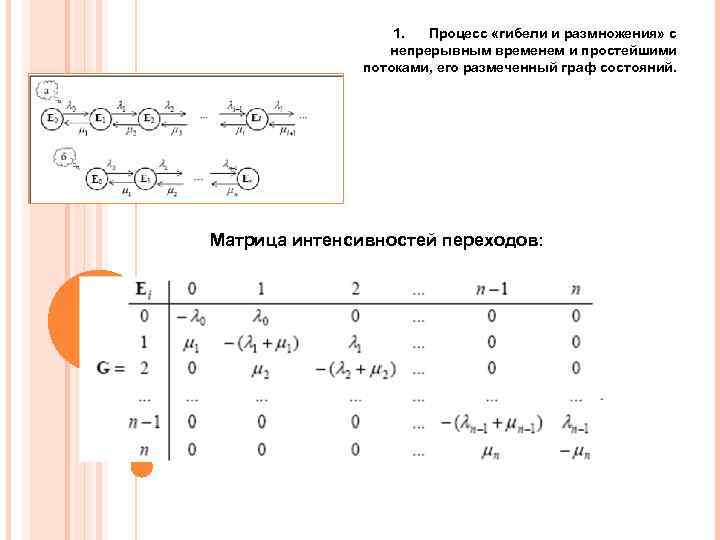1. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф 1. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, его размеченный граф состояний. Матрица интенсивностей переходов: 50 50

Правила составления уравнений для стационарных вероятностей состояний марковского процесса с непрерывным временем Правило 1 Правила составления уравнений для стационарных вероятностей состояний марковского процесса с непрерывным временем Правило 1 (по графу переходов). В левой части каждого уравнения записывается вероятность рассматриваемого состояния, умноженная на сумму интенсивностей переходов из данного состояния во все другие состояния. Правая часть уравнения представляет собой сумму членов, число которых равно числу входящих в данное состояние дуг, и каждый такой член представляет собой произведение интенсивности перехода, соответствующей данной дуге, на вероятность состояния, из которого исходит эта дуга 51 51

Правила составления уравнений для стационарных вероятностей состояний марковского процесса с непрерывным временем Правило 2 Правила составления уравнений для стационарных вероятностей состояний марковского процесса с непрерывным временем Правило 2 (по матрице интенсивностей переходов). Для каждого столбца матрицы интенсивностей переходов составляется соответствующее уравнение как сумма произведений интенсивностей переходов на стационарную вероятность состояния с номером соответствующей строки, приравненная нулю. 52 52

Правила составления уравнений для стационарных вероятностей состояний марковского процесса с непрерывным временем 53 - Правила составления уравнений для стационарных вероятностей состояний марковского процесса с непрерывным временем 53 - стационарные вероятности состояний марковского процесса. - среднее число особей в популяции как математическое ожидание случайной величин 53

Процесс чистого размножения - процесс, у которого интенсивности всех потоков гибели равны нулю. Процесс Процесс чистого размножения - процесс, у которого интенсивности всех потоков гибели равны нулю. Процесс чистой «гибели» - процесс, у которого равны нулю интенсивности всех потоков размножения. Предельные (финальные) вероятности состояний для простейшего эргодического процесса гибели и размножения, находящегося в стационарном режиме: 54 54

55 «Параметры и характеристика систем и сетей массового обслуживания» 55 «Параметры и характеристика систем и сетей массового обслуживания»

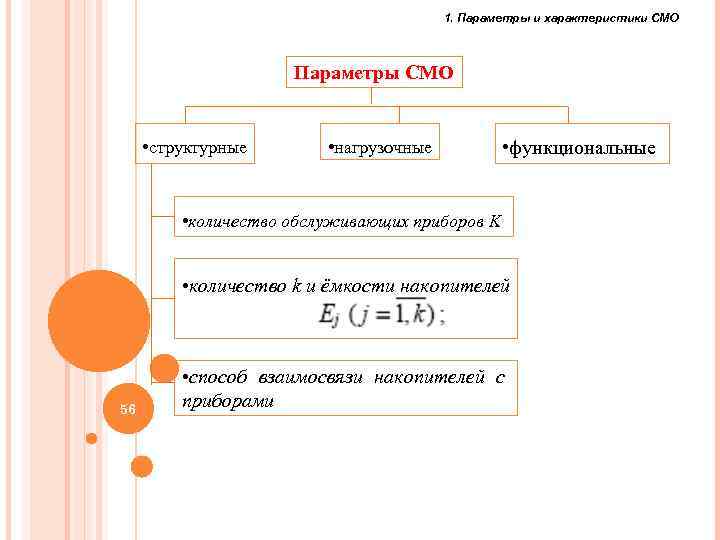1. Параметры и характеристики СМО Параметры СМО • структурные • нагрузочные • функциональные • 1. Параметры и характеристики СМО Параметры СМО • структурные • нагрузочные • функциональные • количество обслуживающих приборов K • количество k и ёмкости накопителей 56 • способ взаимосвязи накопителей с приборами

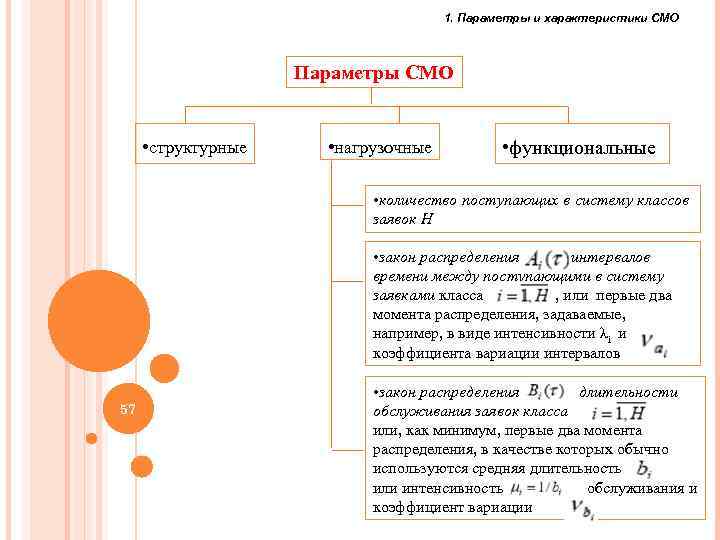1. Параметры и характеристики СМО Параметры СМО • структурные • нагрузочные • функциональные • 1. Параметры и характеристики СМО Параметры СМО • структурные • нагрузочные • функциональные • количество поступающих в систему классов заявок H • закон распределения интервалов времени между поступающими в систему заявками класса , или первые два момента распределения, задаваемые, например, в виде интенсивности λi и коэффициента вариации интервалов 57 • закон распределения длительности обслуживания заявок класса или, как минимум, первые два момента распределения, в качестве которых обычно используются средняя длительность или интенсивность обслуживания и коэффициент вариации

1. Параметры и характеристики СМО Параметры СМО • структурные • нагрузочные • функциональные задаются 1. Параметры и характеристики СМО Параметры СМО • структурные • нагрузочные • функциональные задаются в виде конкретных стратегий управления потоками заявок в СМО, определяющих правило занесения заявок разных классов в накопители ограниченной ёмкости (дисциплина буферизации) и правило выбора их из очереди на обслуживание (дисциплина обслуживания) 58

1. Параметры и характеристики СМО Характеристики СМО с однородным потоком заявок • нагрузка системы: 1. Параметры и характеристики СМО Характеристики СМО с однородным потоком заявок • нагрузка системы: • коэффициент загрузки или просто загрузка системы • коэффициент простоя системы: • вероятность потери заявок: . • 59 вероятность обслуживания заявки 59

1. Параметры и характеристики СМО Характеристики СМО с однородным потоком заявок • производительность системы 1. Параметры и характеристики СМО Характеристики СМО с однородным потоком заявок • производительность системы (интенсивность потока обслуженных заявок, выходящих из системы) • интенсивность потока потерянных (не обслуженных) заявок из-за ограниченной ёмкости накопителя: • среднее время ожидания заявок в очереди: w • среднее время пребывания заявок в системе • средняя длина очереди заявок: • среднее число заявок в системе (в очереди и на обслуживании 60 в приборе): Интегральная оценка - нагрузка Расчет загрузки системы через нагрузку: 60

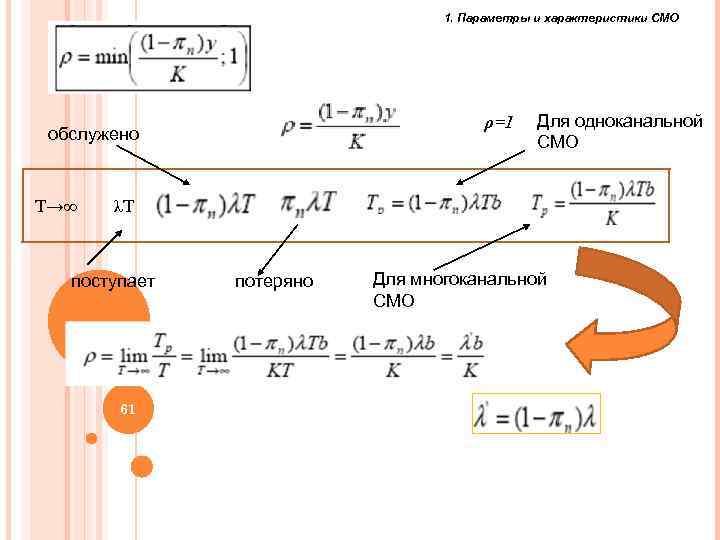1. Параметры и характеристики СМО ρ=1 обслужено T→∞ Для одноканальной СМО λT поступает потеряно 1. Параметры и характеристики СМО ρ=1 обслужено T→∞ Для одноканальной СМО λT поступает потеряно Для многоканальной СМО 61 61

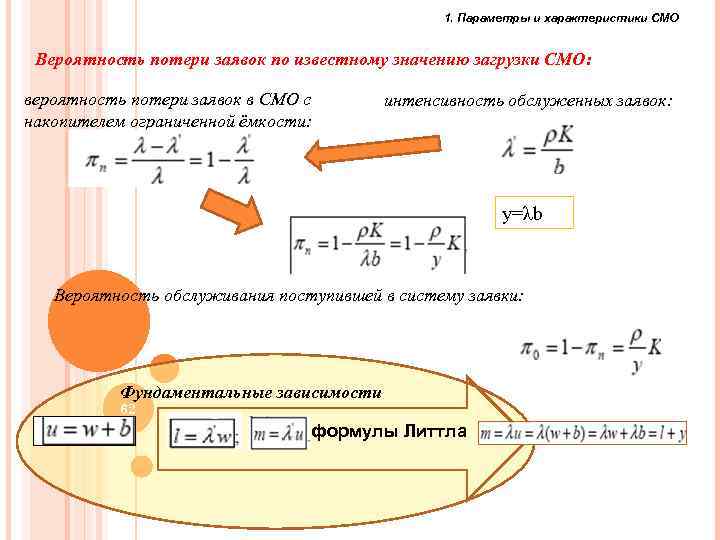1. Параметры и характеристики СМО Вероятность потери заявок по известному значению загрузки СМО: вероятность 1. Параметры и характеристики СМО Вероятность потери заявок по известному значению загрузки СМО: вероятность потери заявок в СМО с накопителем ограниченной ёмкости: интенсивность обслуженных заявок: y=λb Вероятность обслуживания поступившей в систему заявки: Фундаментальные зависимости 62 формулы Литтла 62

1. Параметры и характеристики СМО нагрузка y=λb характеризует среднее число заявок, находящихся на 1. Параметры и характеристики СМО нагрузка y=λb характеризует среднее число заявок, находящихся на обслуживании. отсутствия перегрузок в одноканальной СМО загрузка совпадает с нагрузкой: 63 загрузку одноканальной СМО можно трактовать как среднее число заявок, находящихся на обслуживании в приборе 63

1. Параметры и характеристики СМО Характеристики СМО с неоднородным потоком заявок, в которую поступают 1. Параметры и характеристики СМО Характеристики СМО с неоднородным потоком заявок, в которую поступают H классов заявок с интенсивностями и средними длительностями обслуживания • характеристики по каждому классу (потоку) заявок; • характеристики объединённого (суммарного) потока заявок Характеристики по каждому классу заявок • нагрузка, создаваемая заявками класса • вероятность потери заявок: • вероятность обслуживания заявки: • интенсивность потока обслуженных заявок (производительность по i-му классу заявок): • интенсивность потока потерянных заявок: • загрузка системы, создаваемая заявками класса i: 64 • время ожидания заявок в очереди: wi • время пребывания заявок в системе: • длина очереди заявок: • число заявок в системе (в очереди и на обслуживании): 64

1. Параметры и характеристики СМО Характеристики объединённого (суммарного) потока заявок • суммарная интенсивность поступления 1. Параметры и характеристики СМО Характеристики объединённого (суммарного) потока заявок • суммарная интенсивность поступления заявок в систему (интенсивность суммарного потока): • суммарная нагрузка Y и суммарная загрузка R системы: • коэффициент простоя системы: • среднее время ожидания W и среднее время пребывания U заявок объединённого потока в системе: • суммарная длина очереди и суммарное число заявок в системе: 65 Фундаментальные соотношения 65

Параметры Се. МО 2. Параметры и характеристики Се. МО Описание линейных разомкнутых и замкнутых Параметры Се. МО 2. Параметры и характеристики Се. МО Описание линейных разомкнутых и замкнутых однородных экспоненциальных Се. МО: • число узлов в сети: n; • число обслуживающих приборов в узлах сети: K 1, . . . , Kn ; • матрица вероятностей передач: • интенсивность λ 0 источника заявок, поступающих в разомкнутую Се. МО (РСе. МО), или число заявок M, циркулирующих в замкнутой Се. МО (ЗСе. МО); • средние длительности обслуживания заявок в узлах сети: Характеристики Се. МО • узловые, описывающие эффективность функционирования отдельных узлов 66 Се. МО; • сетевые, описывающие функционирование Се. МО в целом. 66

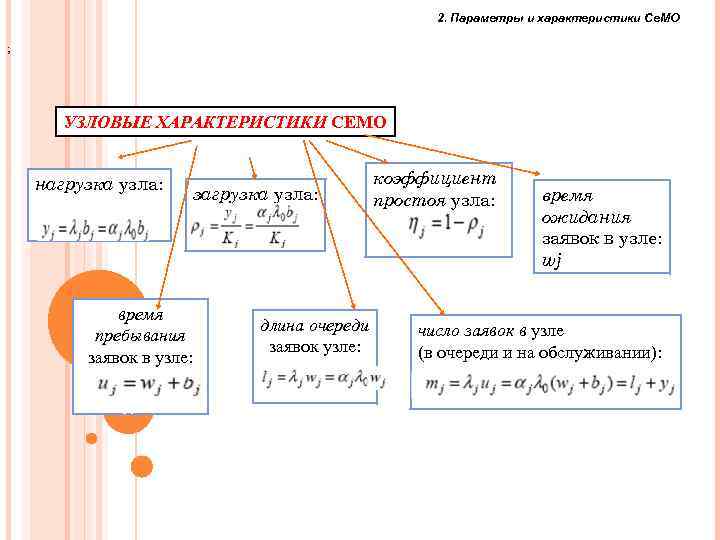2. Параметры и характеристики Се. МО ; УЗЛОВЫЕ ХАРАКТЕРИСТИКИ СЕМО нагрузка узла: загрузка узла: 2. Параметры и характеристики Се. МО ; УЗЛОВЫЕ ХАРАКТЕРИСТИКИ СЕМО нагрузка узла: загрузка узла: время пребывания заявок в узле: длина очереди заявок узле: коэффициент простоя узла: время ожидания заявок в узле: wj число заявок в узле (в очереди и на обслуживании): 67 67

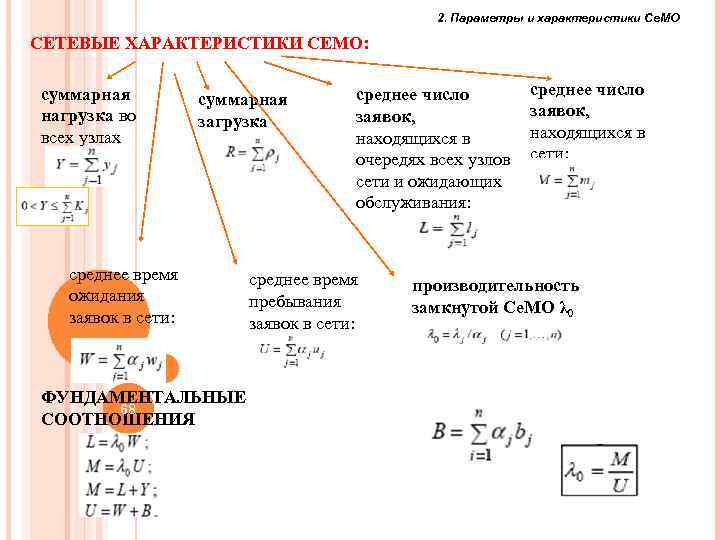2. Параметры и характеристики Се. МО СЕТЕВЫЕ ХАРАКТЕРИСТИКИ СЕМО: суммарная нагрузка во всех узлах 2. Параметры и характеристики Се. МО СЕТЕВЫЕ ХАРАКТЕРИСТИКИ СЕМО: суммарная нагрузка во всех узлах суммарная загрузка среднее время ожидания заявок в сети: среднее число заявок, находящихся в очередях всех узлов сети и ожидающих обслуживания: среднее время пребывания заявок в сети: среднее число заявок, находящихся в сети: производительность замкнутой Се. МО λ 0 ФУНДАМЕНТАЛЬНЫЕ 68 СООТНОШЕНИЯ 68

69 «Методы исследования СМО с простейшими потоками событий. СМО без потерь» 69 «Методы исследования СМО с простейшими потоками событий. СМО без потерь»

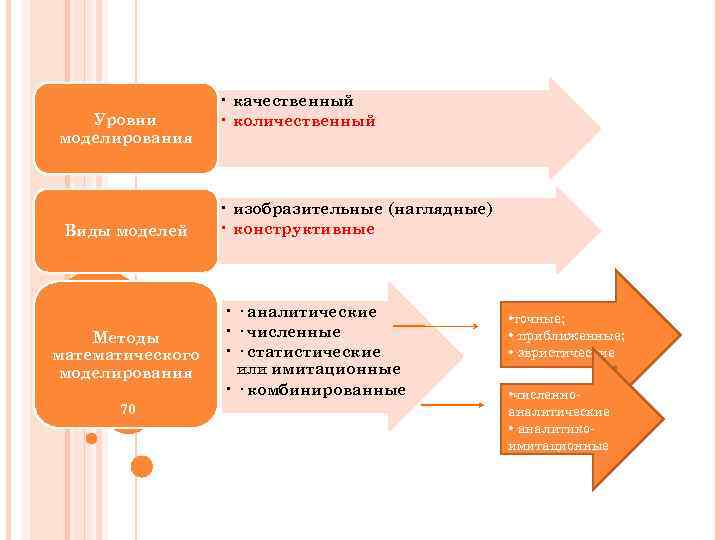Уровни моделирования Виды моделей Методы математического моделирования 70 • качественный • количественный • изобразительные Уровни моделирования Виды моделей Методы математического моделирования 70 • качественный • количественный • изобразительные (наглядные) • конструктивные • · аналитические • · численные • · статистические или имитационные • · комбинированные • точные; • ·приближенные; • ·эвристические • численноаналитические • ·аналитикоимитационные 70

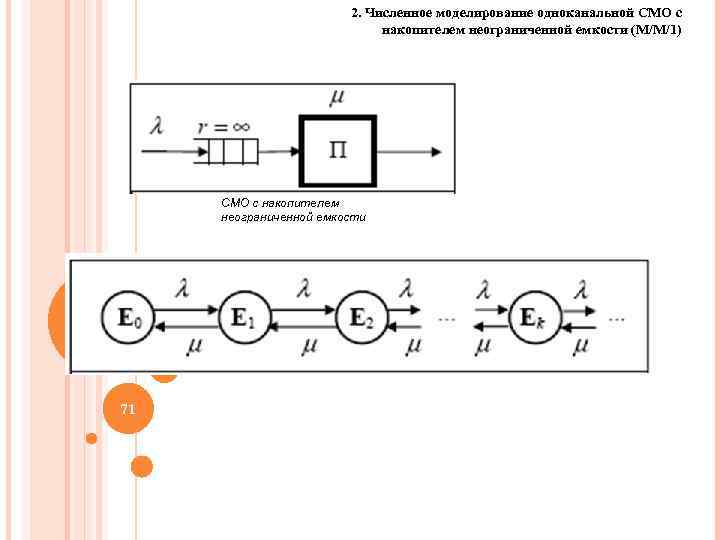2. Численное моделирование одноканальной СМО с накопителем неограниченной емкости (M/M/1) СМО с накопителем неограниченной 2. Численное моделирование одноканальной СМО с накопителем неограниченной емкости (M/M/1) СМО с накопителем неограниченной емкости 71 71

В. Кодирование состояний марковского процесса. E 0 : k = 0 – в системе В. Кодирование состояний марковского процесса. E 0 : k = 0 – в системе нет ни одной заявки; E 1: k = 1 – в системе находится 1 заявка (на обслуживании в приборе); E 2: k = 2 – в системе находятся 2 заявки (одна – на обслуживании в приборе и вторая ожидает в накопителе); … Ek: k – в системе находятся k заявок (одна – на обслуживании в приборе и (k-1) – в накопителе). Д. Система уравнений. 72 72

Е. Расчет характеристик СМО. 1) нагрузка y= / = b; 2) загрузка =1 -p Е. Расчет характеристик СМО. 1) нагрузка y= / = b; 2) загрузка =1 -p 0= b и совпадает с нагрузкой; 3) коэффициент простоя системы η=p 0=1 - 4) среднее число заявок в очереди 5) среднее число заявок в системе 6) вероятность потери заявок =0; 7) производительность системы при отсутствии потерь совпадает с интенсивностью поступления заявок в систему: ’=0 8) интенсивность потерянных заявок : ’’=0 9) среднее время ожидания заявок 73 10) среднее время пребывания заявок u=w+b или 73

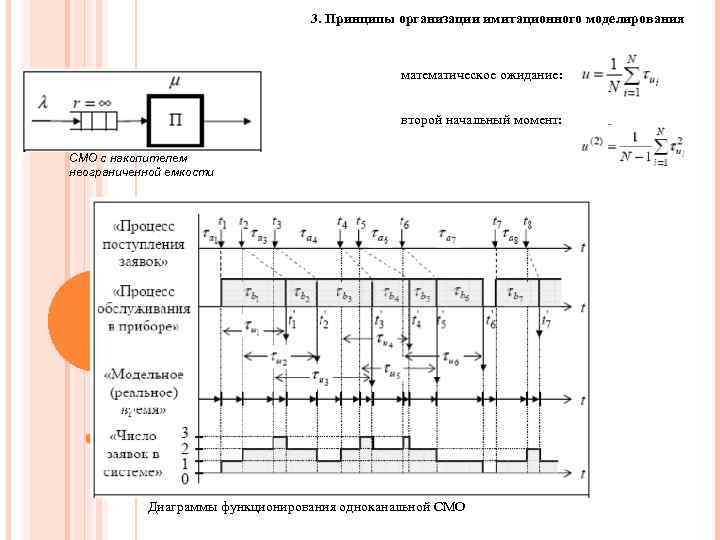3. Принципы организации имитационного моделирования математическое ожидание: второй начальный момент: СМО с накопителем неограниченной 3. Принципы организации имитационного моделирования математическое ожидание: второй начальный момент: СМО с накопителем неограниченной емкости 74 74 Диаграммы функционирования одноканальной СМО

Процедуры имитационного моделирования: 1) выработка (генерирование) случайных величин: • равномерно распределенных; • с заданным Процедуры имитационного моделирования: 1) выработка (генерирование) случайных величин: • равномерно распределенных; • с заданным законом распределения; 2) формирование потоков заявок и имитация обслуживания; 3) организация очередей заявок; 4) организация службы времени; 5) сбор и статистическая обработка результатов моделирования. Методы формирования равномерно распределённых случайных величин в интервале (0; 1): • метод квадратов; • метод произведений; 75 • мультипликативный конгруэнтный метод; • методы, представляющие модификации перечисленных методов. 75

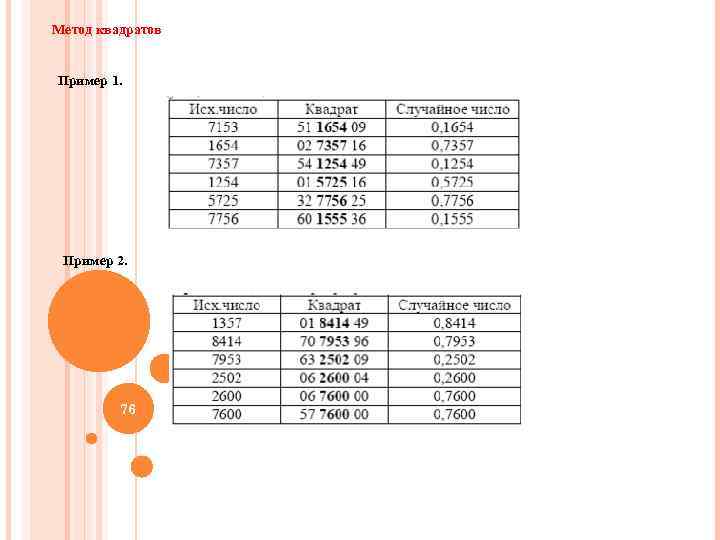Метод квадратов Пример 1. Пример 2. 76 76 Метод квадратов Пример 1. Пример 2. 76 76

Метод произведений Пример 3. Ядро = 5167; множитель = 3729 Конгруэнтные методы 2568 и Метод произведений Пример 3. Ядро = 5167; множитель = 3729 Конгруэнтные методы 2568 и 148 (по модулю 10), 1746 и 511 (по модулю 5), 6493 и 2221 ( по модулю 2) Пример 4. 77 77

Проверка генераторов равномерно распределенных псевдослучайных чисел · на периодичность; · на случайность; · на Проверка генераторов равномерно распределенных псевдослучайных чисел · на периодичность; · на случайность; · на равномерность. определение длины периода тесты проверки: · частот; · пар; · комбинаций; · серий; · корреляции. тест проверки частот 78 78

«НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Q-СХЕМЫ)» 79 «НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Q-СХЕМЫ)» 79

1. Одноканальная СМО без накопителя (M/M/1/0) 2. Многоканальная СМО без накопителя (M/M/N/0) 3. Одноканальная 1. Одноканальная СМО без накопителя (M/M/1/0) 2. Многоканальная СМО без накопителя (M/M/N/0) 3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1) 80

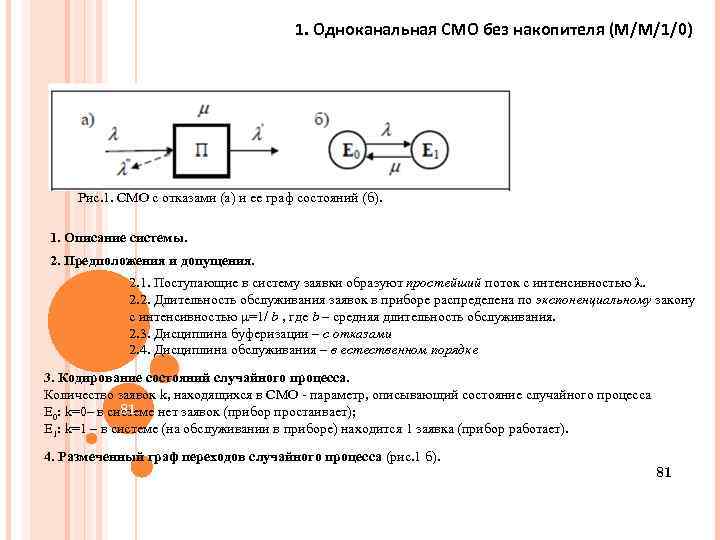1. Одноканальная СМО без накопителя (M/M/1/0) Рис. 1. СМО с отказами (а) и ее 1. Одноканальная СМО без накопителя (M/M/1/0) Рис. 1. СМО с отказами (а) и ее граф состояний (б). 1. Описание системы. 2. Предположения и допущения. 2. 1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ. 2. 2. Длительность обслуживания заявок в приборе распределена по экспоненциальному закону с интенсивностью =1/ b , где b – средняя длительность обслуживания. 2. 3. Дисциплина буферизации – с отказами 2. 4. Дисциплина обслуживания – в естественном порядке 3. Кодирование состояний случайного процесса. Количество заявок k, находящихся в СМО - параметр, описывающий состояние случайного процесса 81 E 0: k=0– в системе нет заявок (прибор простаивает); E 1: k=1 – в системе (на обслуживании в приборе) находится 1 заявка (прибор работает). 4. Размеченный граф переходов случайного процесса (рис. 1 б). 81

1. Одноканальная СМО без накопителя (M/M/1/0) 5. Диаграммы функционирования системы. 'Рис. 2. Диаграммы процессов 1. Одноканальная СМО без накопителя (M/M/1/0) 5. Диаграммы функционирования системы. 'Рис. 2. Диаграммы процессов в СМО с отказами а) поступления в СМО заявок, интервалы между которыми в случае простейшего потока распределены по экспоненциальному закону; б) перехода из состояния Е 0 в состояние Е 1 и обратно, в которых может находиться система; в) выхода из системы обслуженных заявок в моменты времени г) выхода из системы необслуженных заявок, получивших отказ из-за занятости прибора в моменты времени ' 82 д) формирования интервалов времени между соседними переходами случайного процесса. 82

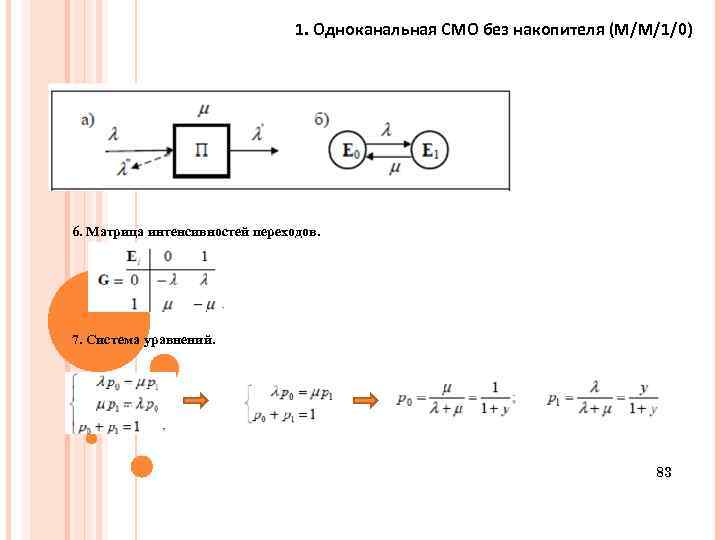1. Одноканальная СМО без накопителя (M/M/1/0) 6. Матрица интенсивностей переходов. 7. Система уравнений. 83 1. Одноканальная СМО без накопителя (M/M/1/0) 6. Матрица интенсивностей переходов. 7. Система уравнений. 83 83

, 1. Одноканальная СМО без накопителя (M/M/1/0) ; 8. Расчет характеристик СМО. 1) , 1. Одноканальная СМО без накопителя (M/M/1/0) ; 8. Расчет характеристик СМО. 1) нагрузка: y=λ/ =λb 2) загрузка определяется как вероятность работы прибора: ρ=p 1 и не совпадает с нагрузкой 3) коэффициент простоя системы 4) среднее число заявок в системе: m=p 1=ρ 5) вероятность потери заявок в результате отказа в обслуживании из-за занятости прибора 6) производительность системы: 7) интенсивность потока не обслуженных заявок, то есть получивших отказ: 8) среднее время пребывания заявок в системе: 9. Анализ свойств системы. 84 84

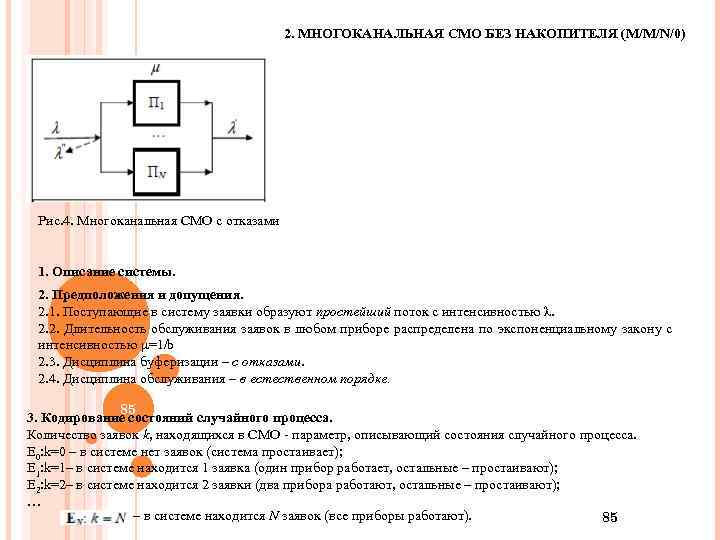2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0) Рис. 4. Многоканальная СМО с отказами 1. Описание 2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0) Рис. 4. Многоканальная СМО с отказами 1. Описание системы. 2. Предположения и допущения. 2. 1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ. 2. 2. Длительность обслуживания заявок в любом приборе распределена по экспоненциальному закону с интенсивностью =1/b 2. 3. Дисциплина буферизации – с отказами. 2. 4. Дисциплина обслуживания – в естественном порядке. 85 3. Кодирование состояний случайного процесса. Количество заявок k, находящихся в СМО - параметр, описывающий состояния случайного процесса. E 0: k=0 – в системе нет заявок (система простаивает); E 1: k=1– в системе находится 1 заявка (один прибор работает, остальные – простаивают); E 2: k=2– в системе находится 2 заявки (два прибора работают, остальные – простаивают); … – в системе находится N заявок (все приборы работают). 85

2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0) 4. Размеченный граф переходов случайного процесса 5. Матрица 2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0) 4. Размеченный граф переходов случайного процесса 5. Матрица интенсивностей переходов. 6. Система уравнений. 86 86

2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0) , 7. Расчет характеристик СМО. 1) нагрузка: y=λ/ 2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0) , 7. Расчет характеристик СМО. 1) нагрузка: y=λ/ =λb (по определению); 2) загрузка 3) коэффициент простоя системы: 4) среднее число заявок в системе 5) среднее число простаивающих приборов: 6) вероятность отказа в обслуживании 87 7) производительность системы 8) интенсивность потока не обслуженных заявок 9) среднее время пребывания заявок в системе 8. Анализ свойств системы. 87

3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 1. Описание системы. 2. Предположения и 3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 1. Описание системы. 2. Предположения и допущения. 2. 1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ. 2. 2. Длительность обслуживания заявок в приборе распределена по экспоненциальному закону с интенсивностью =1/b. 2. 3. Дисциплина буферизации – с потерями 2. 4. Дисциплина обслуживания –по правилу FIFO. 3. Кодирование состояний марковского процесса. Количество заявок k, находящихся в СМО (в приборе и в накопителе) - параметр, описывающий состояние марковского процесса. E 0: k=0 – в системе нет ни одной заявки; E 1: k=1 – в системе находится 1 заявка на обслуживании в приборе; 88 E 2: k=2 – в системе находятся 2 заявки: одна – на обслуживании в приборе и вторая ожидает в накопителе; … Er+1: k=r+1 – в системе находятся ( r +1) заявок: одна – на обслуживании в приборе и r – в накопителе. 88

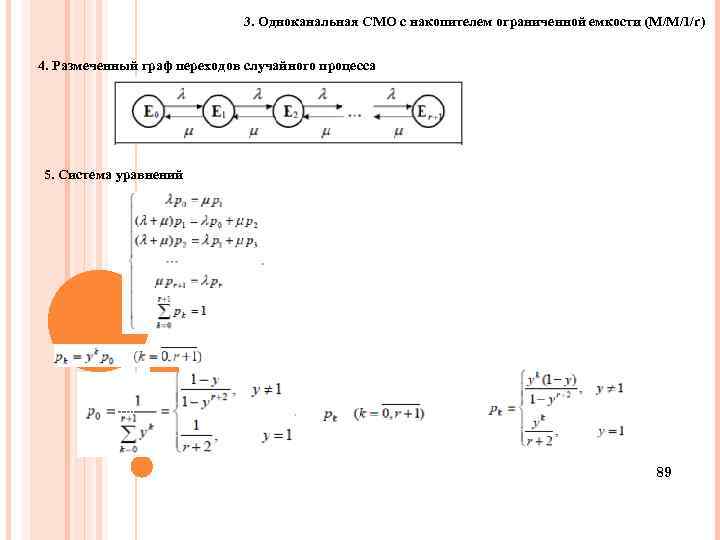3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 4. Размеченный граф переходов случайного процесса 3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 4. Размеченный граф переходов случайного процесса 5. Система уравнений 89 89

3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 5. Расчет характеристик СМО. . 1) 3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r) 5. Расчет характеристик СМО. . 1) нагрузка y=λ/ =λb; 2) загрузка 3) коэффициент простоя системы 4) среднее число заявок в очереди 5) среднее число заявок в системе 6) вероятность потери заявок 7) производительность системы (интенсивность потока обслуженных заявок) 8) интенсивность потока потерянных заявок 9) среднее время ожидания заявок 10) среднее время пребывания заявок 90 90

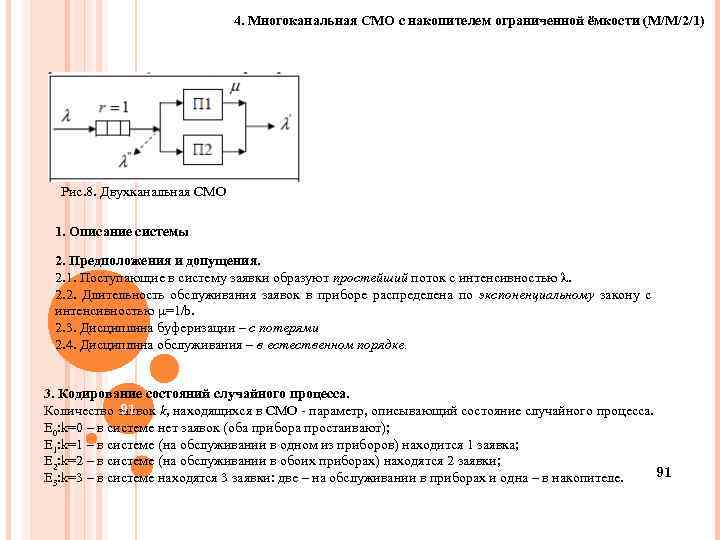4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1) Рис. 8. Двухканальная СМО 1. Описание 4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1) Рис. 8. Двухканальная СМО 1. Описание системы 2. Предположения и допущения. 2. 1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ. 2. 2. Длительность обслуживания заявок в приборе распределена по экспоненциальному закону с интенсивностью =1/b. 2. 3. Дисциплина буферизации – с потерями 2. 4. Дисциплина обслуживания – в естественном порядке. 3. Кодирование состояний случайного процесса. 91 Количество заявок k, находящихся в СМО - параметр, описывающий состояние случайного процесса. E 0: k=0 – в системе нет заявок (оба прибора простаивают); E 1: k=1 – в системе (на обслуживании в одном из приборов) находится 1 заявка; E 2: k=2 – в системе (на обслуживании в обоих приборах) находятся 2 заявки; 91 E 3: k=3 – в системе находятся 3 заявки: две – на обслуживании в приборах и одна – в накопителе.

4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1). 4. Размеченный граф переходов случайного процесса 4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1). 4. Размеченный граф переходов случайного процесса 5. Расчет характеристик СМО. 1) нагрузка: y=λ/ =λ/b 2) загрузка: 3) среднее число работающих приборов: 4) коэффициент простоя системы: 5) среднее число заявок в очереди: 6) среднее число заявок в системе: 7) вероятность потери заявок: 8) производительность системы (интенсивность потока обслуженных заявок): 92 9) интенсивность потока потерянных заявок: 10) среднее время ожидания заявок: 11) среднее время пребывания заявок: 92