Методы исследования и моделирования экономики Фаддеенков А В

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Простая линейная модель международной торговли Страна 3 Страна 2 Страна 1 Страна n 1

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Денежные и материальные потоки в модели международной торговли доход Страна j Другие страны 2

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Матрица обмена – Доля дохода страны j, которая тратится на торговлю со страной i. (1) ОПРЕДЕЛЕНИЕ Матрица A, состоящая из элементов , удовлетворяющих условиям (1) называется матрицей обмена. 3

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент – Вектор доходов, получаемых странами 1, 2, … , n от торговли между собой. ЗАДАЧА: Дана матрица обмена A. Существует ли полуположительный вектор y, удовлетворяющий условию (2) ? (2) 4

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ОПРЕДЕЛЕНИЕ Вектор y, удовлетворяющий условию (2) называется равновесным вектором. ТЕОРЕМА 1 (теорема существования) Если A – матрица обмена, то полуположительный вектор y, удовлетворяющий условию (2) существует всегда. 5

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ? (3) (2) Когда это уравнение не имеет решения? Из линейной алгебры известно, что уравнение (3) не имеет решения только в том случае, если существует такой вектор x, для которого выполняется неравенство: (4) Поскольку A – матрица обмена, то верно равенство: (5) , где 6

Методы исследования и моделирования экономики Обозначим Фаддеенков А. В. к. т. н. , доцент и пусть Если умножить (5) на и вычесть полученное равенство из (4), то мы придем к соотношению: вектор Для самого первого элемента: Но это НЕВОЗМОЖНО, т. к. 7

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Независимые подмножества стран 8

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ОПРЕДЕЛЕНИЕ Говорят, что страны образуют независимое подмножество S, если в матрице обмена 9

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ОПРЕДЕЛЕНИЕ Матрица обмена называется неприводимой, если в ней не существует отличных от N непустых независимых подмножеств Из неприводимости следует, что все страны торгуют между собой, хотя, может быть, и «косвенно» . импорт товаров 10

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент УПРАЖНЕНИЕ Доказать, что матрица обмена A неприводима в том и только в том случае, если для любых двух индексов Существует последовательность такая, что Доказать самостоятельно 11

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ТЕОРЕМА 2 Если матрица обмена A неприводима, то соответствующий ей равновесный вектор y оказывается положительным и единственным с точностью до сомножителя. Сначала покажем, что вектор y положителен. Допустим обратное. 12

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент S – независимое подмножество; но A – неприводимая и, следовательно, S совпадает с N. Теперь покажем, что вектор y единственный. Пусть существует другой равновесный вектор Если положить Но вектор то не является положительным, т. к. то есть 13

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ОПРЕДЕЛЕНИЕ Независимое подмножество, содержащееся в другом независимом подмножестве называется собственным. ОПРЕДЕЛЕНИЕ Независимое подмножество называется неприводимым, если в нем не содержится другого независимого подмножества. 14

Методы исследования и моделирования экономики ЛЕММА 1 Если S и T – независимые подмножества, то их пересечение и их объединение также будут независимыми подмножествами. Фаддеенков А. В. к. т. н. , доцент – независимые Пусть Если при таких i и j , или то мы все доказали! – независимое 15

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Вторая часть леммы доказывается аналогично (сделать самостоятельно). УПРАЖНЕНИЕ Различные неприводимые подмножества N не пересекаются, т. е. Если S и T – неприводимые и то Доказать самостоятельно 16

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент – неприводимые подмножества – оставшиеся страны 17

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Неприводимая матрица определим 18

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент – равновесный вектор для всей модели тоже равновесный вектор для всей модели Всякий ли равновесный вектор можно представить в таком виде? ? 19

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ТЕОРЕМА 3 Пусть A – матрица обмена с неприводимыми подмножествами , – равновесный вектор. Тогда где , – равновесный вектор, соответствующий множеству. Доказывать не будем. 20

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Следствие из ТЕОРЕМЫ 3 Если некоторая i-ая страна не принадлежит никакому независимому подмножеству, то для всех решений уравнения Ay= y будет выполняться условие: РЕЗЮМЕ 21

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент – заданные начальные доходы – доходы после одного тура обмена – доходы после двух туров обмена – доходы после k туров обмена Существует ли предел, и если да, то как он зависит от начального распределения доходов? ? 22

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Будем говорить, что последовательность векторов сходится к вектору если последовательности чисел сходятся к ОПРЕДЕЛЕНИЕ Матрица обмена A называется устойчивой, если существует такой неотрицательный вектор , что для любого , удовлетворяющего условию последовательность сходится к . 23

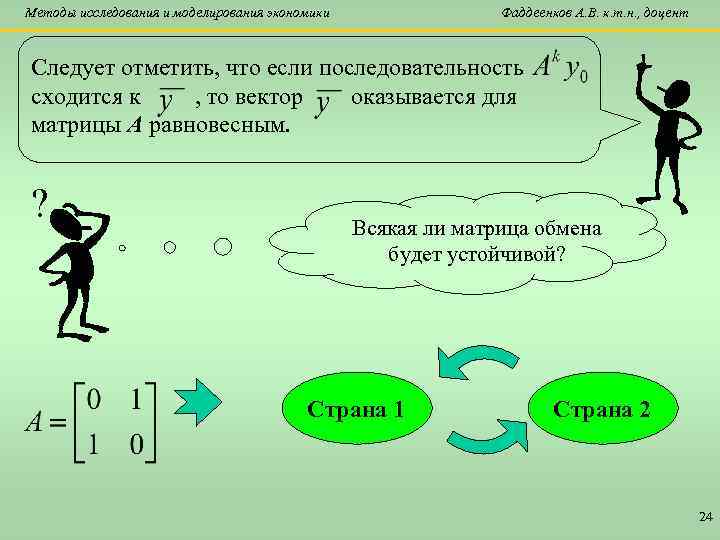Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Следует отметить, что если последовательность сходится к , то вектор оказывается для матрицы A равновесным. ? Всякая ли матрица обмена будет устойчивой? Страна 1 Страна 2 24

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ОПРЕДЕЛЕНИЕ Матрица обмена A называется периодической, если можно так разбить множество всех стран на подмножества что ОПРЕДЕЛЕНИЕ Число m в этом случае называется периодом матрицы A. 25

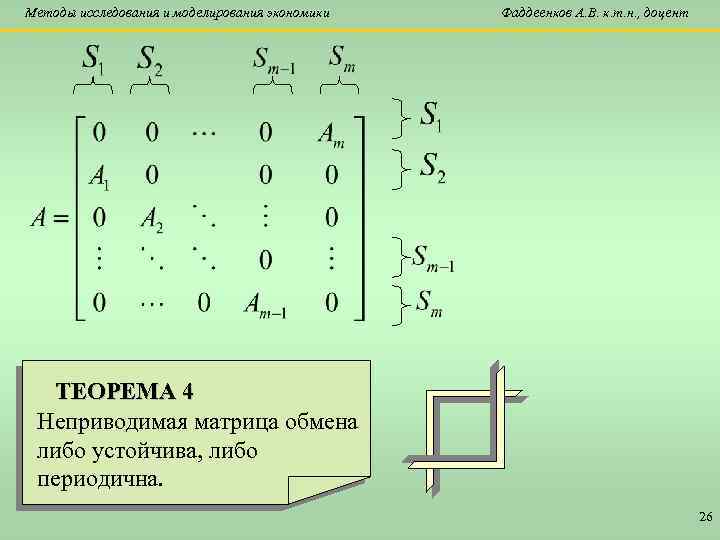Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент ТЕОРЕМА 4 Неприводимая матрица обмена либо устойчива, либо периодична. 26

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент – не принадлежат ни одному неприводимому подмножеству Неприводимые подмножества A= 0 D 27

Методы исследования и моделирования экономики Фаддеенков А. В. к. т. н. , доцент Количество денег, получаемое i-й страной от стран, не входящих ни в одно неприводимое подмножество, за бесконечное число туров обмена: 28