Методика статистической обработки результатов • На

Методика статистической обработки результатов

• На каждом измеряемом объекте проводят не меньше 25 измерений одного параметра. • Количество измерений обозначается латинской буквой n. • Каждое значение называется вариантой и обозначается латинской буквой xi.

1. Получив ряд цифр, необходимо найти среднюю величину (сложить значение вариант и разделить на их количество):

2. Каждое конкретное значение варианты отличается от на какую-то величину в сторону + или -. Поэтому очень важным значением является среднее квадратическое отклонение. Обозначается латинской буквой сигма (σ) и определяется:

3. σ – это показатель варьирования, его легче оценить, рассчитав коэффициент вариации Сv: Если Сv больше 10% – варьирование малое, если 10 -30% – варьирование среднее, если больше 30% – варьирование сильное. При сильном варьировании надо увеличить количество измерений и вновь пересчитать.

4. Определение каждой среднеарифметической происходит с какой-либо ошибкой – m , которая определяется:

После этого средняя величина записывается как: Средняя величина даже с учетом ошибки не всегда достоверна. Если превышает свою ошибку в 3 раза, то она достоверна. Если она не достоверна, то надо увеличить количество измерений.

5. Средняя ошибка m – показатель точности, но выраженный в единицах измерения (м, см, мм и т. п. ). Если ее выразить в процентах от средней величины, то получим показатель точности (р), а именно: Чем меньше этот показатель, тем с большей точностью определена средняя арифметическая.

6. Если один и тот же показатель зависим от разных условий, то чтобы узнать степень влияния этих условий, находят различие между средними величинами этого показателя – достоверность различий (t – критерий Стьюдента). Если t больше 3, различие достоверно, t меньше 3 – различие недостоверно.

7. Для выявления связи между показателями определяется коэффициент корреляции (r). Коэффициент корреляции — это мера взаимосвязи измеренных явлений. Методами корреляционного анализа решаются следующие задачи: 1) Взаимосвязь. Есть ли взаимосвязь между параметрами? 2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым. 3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.

Коэффициент корреляции (обозначается «r» ) рассчитывается по специальной формуле и изменяется от -1 до +1. Показатели, близкие к +1, говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной. Показатели, близкие к -1, свидетельствуют об обратной связи, т. е. При увеличении значений одной переменной, значения другой уменьшаются.

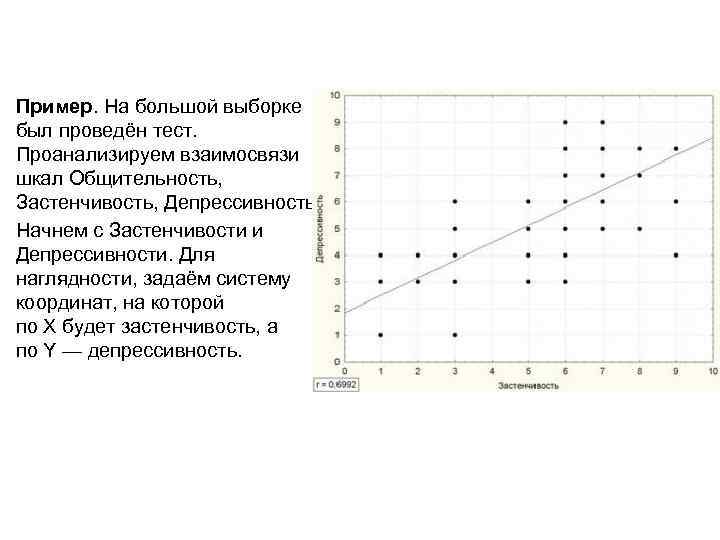
Пример. На большой выборке был проведён тест. Проанализируем взаимосвязи шкал Общительность, Застенчивость, Депрессивность. Начнем с Застенчивости и Депрессивности. Для наглядности, задаём систему координат, на которой по X будет застенчивость, а по Y — депрессивность.

Таким образом, каждый человек из выборки исследования может быть изображен точкой на этой системе координат. В результате расчетов, коэффициент корреляции между ними r=0, 6992. Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны.

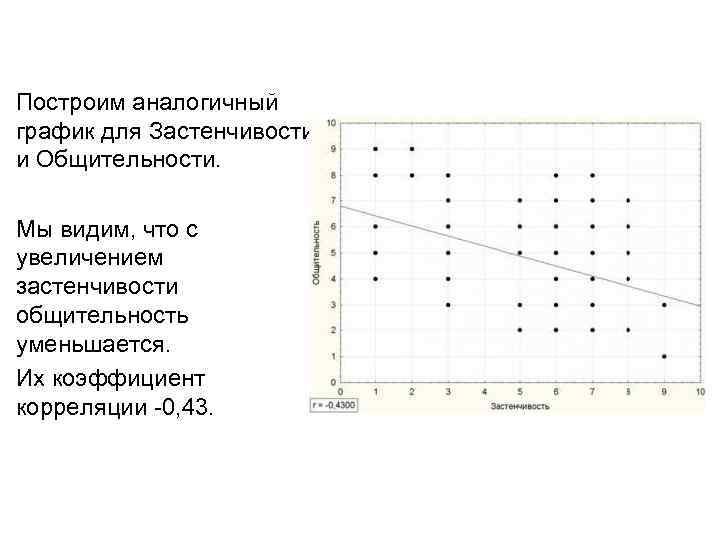
Построим аналогичный график для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0, 43.

Таким образом, коэффициент корреляции от 0 до 1, говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 – обратнопропорциональной (чем больше… тем меньше…) Если бы точки были расположены хаотично, коэффициент корреляции приближался бы к 0. Коэффициент корреляции отражает степень приближенности точек на графике к прямой.

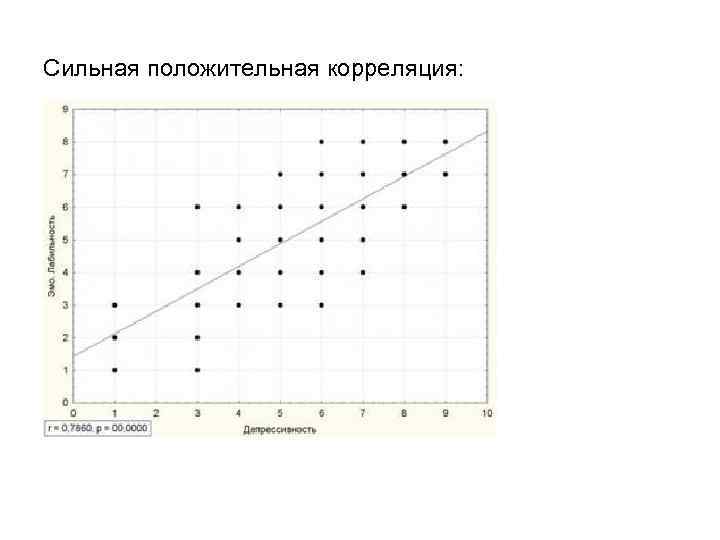
Сильная положительная корреляция:

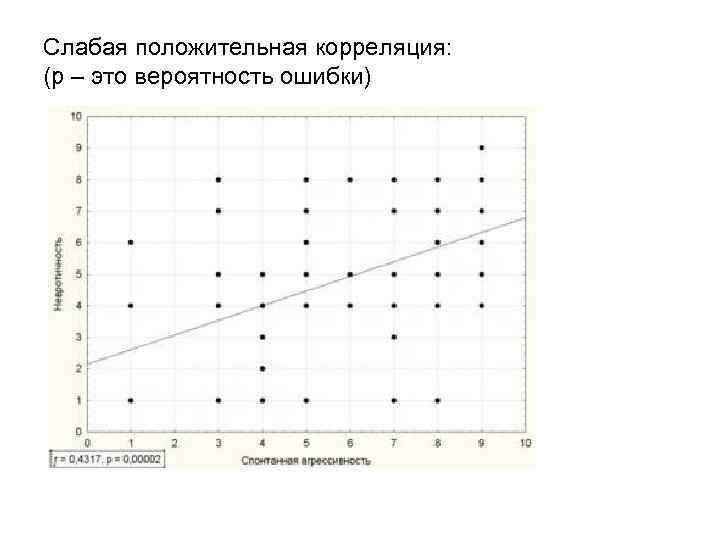
Слабая положительная корреляция: (p – это вероятность ошибки)

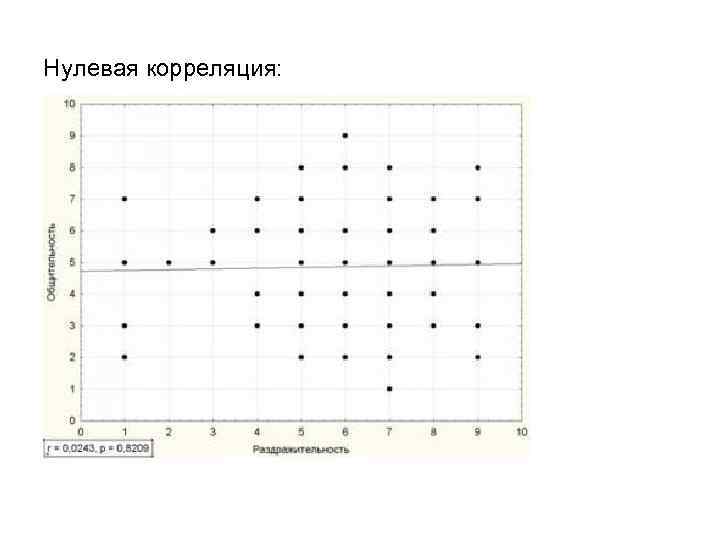
Нулевая корреляция:

Виды взаимосвязи • Прямая положительная и отрицательная взаимосвязь. Два явления непосредственно совпадают, поэтому взаимосвязаны. Интеллект и успеваемость в школе, общительность и застенчивость — яркие примеры прямой взаимосвязи. • Косвенная взаимосвязь. Два явления сильно коррелируют с третьим, поэтому между собой так же имеют корреляцию. К примеру, стиль общения ребенка взаимосвязан со стилем воспитания в семье за счет третьей переменной — установок личности. Очевидно, что воспитание в семье формирует установки ребенка, в свою очередь установки влияют на поведение. • Нулевая корреляция. Предполагает отсутствие закономерной взаимосвязи между переменными. • Случайная взаимосвязь. Корреляция может быть случайной! Очень многие процессы происходят одновременно и совпадают. Здесь уместно сказать, что если много-много коррелировать — что-нибудь обязательно скоррелируется.