Методика преподавания математики в коррекционной школе Задачи

Методика преподавания математики в коррекционной школе

Задачи обучения • Коррекционно-образовательная • Коррекционно-развивающая • Коррекционно-воспитательная

Особенности усвоения математических знаний • • • Мышление Речь Восприятие Память Моторика Внимание

Специфические нарушения счетных операций • Дискалькулия • Акалькулия

Структура математического материала • Арифметика • нумерация • арифметические действия • решение задач • величины • Геометрия

Содержание математического материала 1. 2. 3. 4. 5. 6. 1 -10 – 1 класс 1 -100 (до 20) - 2 класс, до 100 – 3 - 4 класс 1 – 1000 – 5 класс 1 – 10 000 - 6 класс 1 – 100 000 – 7 класс 1 – 1000 – 8 - 9 класс

Методы обучения математике перцептивные • словесные • наглядные • практические логические • индуктивный • дедуктивный гностические • репродуктивный • поисковый • исследовательский

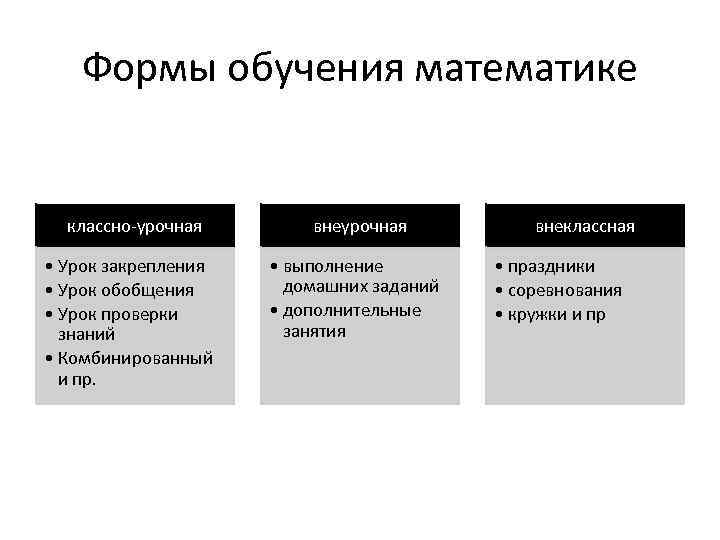Формы обучения математике классно-урочная • Урок закрепления • Урок обобщения • Урок проверки знаний • Комбинированный и пр. внеурочная • выполнение домашних заданий • дополнительные занятия внеклассная • праздники • соревнования • кружки и пр

Структура комбинированного урока 1. 2. 3. 4. Организация учащихся на урок. Проверка домашнего задания Устный счет Актуализация опорных знаний для подведения к восприятию нового материала 5. Сообщение темы, целей урока. Сообщение нового материала учителем, восприятие и первичное осознание его уч-ся 6. Первичное закрепление новых знаний и включение их в систему имеющихся у уч-ся знаний. 7. Практическая работа учащихся под руководством учителя и в самостоятельной деятельности 8. Повторение, обобщение и систематизация имеющихся знаний. 9. Объяснение домашнего задания 10. Подведение итогов.

Задачи пропедевтического периода • Выявление уровня подготовленности к обучению математики • Подготовка учащихся к обучению математики

Содержание пропедевтического периода • • Формирование понятия о величине Формирование понятия о количестве Формирование пространственных понятий Понимание предлогов Формирование временных понятий Развитие графических навыков Формирование сенсорных эталонов

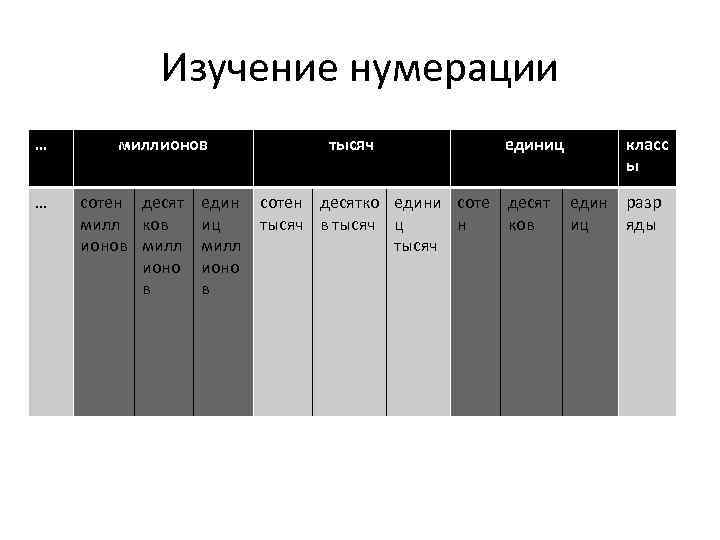Изучение нумерации … миллионов … сотен десят един милл ков иц ионов милл ионо в в тысяч единиц сотен десятко едини соте десят тысяч в тысяч ц н ков тысяч класс ы един разр иц яды

Программные требования по изучению нумерации • Владение прямым и обратным счетом • Нахождение недостающего числа в числовом ряду • Сравнение чисел • Округление чисел • Уметь разбирать число по разрядам • Уметь составлять число из разрядов • Уметь представлять число в виде суммы разрядных слагаемых

Последовательность изучения нумерации в пределах 20 1. Прибавление одного предмета к известному множеству 2. Знакомство с новым множеством и числом, обозначающим это множество 3. Знакомство с цифрой (записью числа) 4. Отработка прямого и обратного счета

Последовательность изучения нумерации в пределах 100 1. Изучение последовательности круглых десятков 2. Изучение нумерации внутри каждого десятка 3. Получение и запись любого двузначного числа 4. Отработка всех случаев перехода через десяток

Последовательность изучения нумерации многозначных чисел 1. Получение круглых чисел 2. Получение и анализ полных чисел 3. Получение и анализ неполных чисел 4. Счет разрядными единицами и равными числовыми группами 5. Отработка случаев перехода через разряд

Программные требования по изучению арифметических действий • Владение отвлеченными счетными операциями • Владение 4 арифметическими действиями в пределах 1 миллиона (действия 1 и 2 ступени) • Владение устными и письменными вычислениями • Знать компоненты действий • Знать простейшие математические законы

Последовательность изучения счетных операций в пределах 10 1. а+1 2. а-1 3. а+2 4. а-2 4. Состав числа

Изучение состава числа 1. Деление множества на 2 подмножества 2. Запись пар чисел 3. Заучивание пар чисел 4. Составление примеров на сложение, вычитание, примеров с неизвестным

Последовательность изучения счетных операций в пределах 20 1. а+1 2. а-1 3. а+2 4. а-2 5. Решение примеров, основанных на знании разрядного состава 6. Сложение единиц двузначного числа с единицами 7. Вычитание единиц из единиц двузначного числа 8. Решение примеров, в ответе которых получается новый десяток или раздробляется десяток 9. Сложение и вычитание чисел с переходом через разряд

Последовательность изучения сложения в пределах 100 с переходом через разряд круглых десятков (50+40) круглых десятков с единицами (50+4) круглых десятков с полным двузначным числом (50+ 24) полного двузначного числа с единицами (54+3) полного двузначного числа с полным двузначным числом (54+23) полного двузначного числа с единицами так, чтобы в ответе получился новый десяток (54+6) • полного двузначного числа с полным двузначным числом так, чтобы в ответе получился новый десяток (54+36) • полного двузначного числа с единицами с переходом через разряд (54+7) • полного двузначного числа с полным двузначным числом с переходом через разряд (54+37) • • •

Последовательность изучения вычитания в пределах 100 с переходом через разряд 70 -40 2. 78 -8, 78 -70 3. 78 -4 4. 78 -34 5. 70 -3 6. 70 -23 7. 73 -5 8. 73 -25 1.

Письменного сложение и вычитание 1. 248+314 2. 154+567 3. 575+328 1. 376 -183 2. 434 -165 3. 306 -168

Табличное умножение и деление • • 2+2=4 2 х2=4 2+2+2=6 2 х3=6 2+2+2+2=8 2 х4=8 …………… 4: 2=2 6: 2=3 8: 2=4 ………

Внетабличное умножение на однозначное число 1. 28 х3 2. 69 х4 3. 263 х2 4. 275 х2

Внетабличное деление на однозначное число 1. 373: 3 2. 531: 3 3. 153: 3 4. 318: 3

Алгоритм письменного деления 1. Определить неполное делимое 2. Определить количество знаков в частном 3. Разделить первое неполное делимое, умножить, получить остаток 4. Проверить остаток, он должен быть меньше делителя 5. Перенести только одну следующую цифру

Действия с величинами Без преобразования • • • 3 м 80 см + 12 см 3 м 80 см – 24 см 2 кг 150 г х 3 20 р 45 к : 5 6 ч 28 мин +25 мин С преобразованием • • • 3 м 80 см +20 см 3 м 20 см – 24 см 2 кг 150 г х 8 2 р 45 к : 5 6 ч 28 мин +46 мин

Классификация задач по форме • • Приведенная Неприведенная Прямая Обратная С лишними числовыми данными С недостающими числовыми данными Некорректно сформулированная В стихотворной форме

Классификация простых задач по содержанию • Раскрывающие конкретный смысл арифметических действий • Раскрывающие различные отношения между числами • Раскрывающие связи между компонентами и результатами арифметических действий • Раскрывающие понятия о величинах • Геометрического содержания

Этапы решения задач 1. Восприятие и анализ содержания 2. Составление плана решения 3. Выполнение плана решения 4. Формирование ответа 5. Проверка решения

Программные требования по изучению геометрического материала • Иметь геометрические представления (прямая, луч, угол, плоские, объемные фигуры) • Знать их основные свойства • Уметь вычислять периметр, площадь, объем • Владеть навыками измерения и черчения