МЕТОДИКА ПОДГОТОВКИ К РЕШЕНИЮ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ С НЕОДНОЗНАЧНОСТЬЮ

МЕТОДИКА ПОДГОТОВКИ К РЕШЕНИЮ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ С НЕОДНОЗНАЧНОСТЬЮ В УСЛОВИИ (многовариантные задачи, типовые задания С 4)

Тренировочный вариант 15 7. Точка В – середина отрезка АС, причем AC = 6. Проведены три окружности радиуса 5 с центрами А, В и С. Найдите радиус четвертой окружности, касающейся всех трех данных.

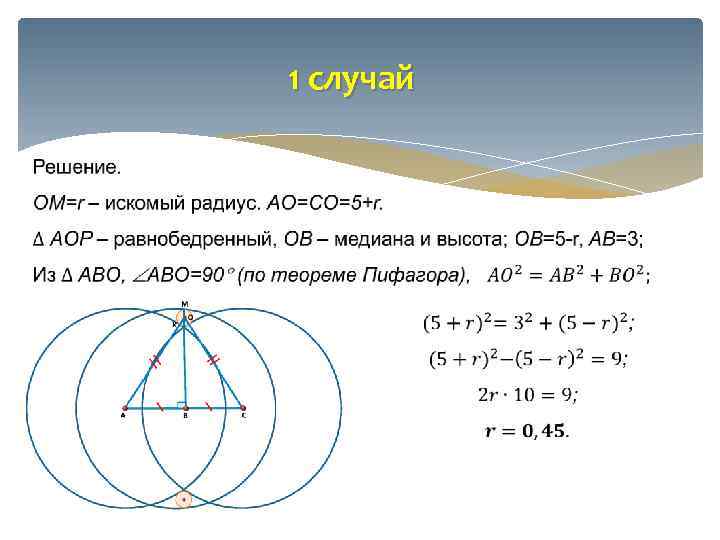1 случай

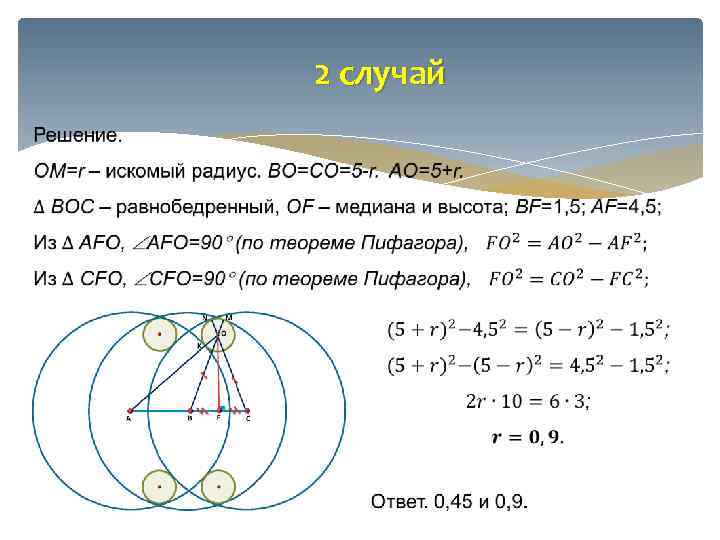2 случай

Тренировочный вариант 16 8. В окружности проведены хорды KL, MN, PS. Хорды KL, PS пересекаются в точке С, хорды KL, MN пересекаются в точке А, хорды MN и PS пересекаются в точке В, причем AL = CK , AM= BN , BS = 5 , BC = 4. Найдите радиус окружности, если величина угла ВАС равна 45 градусов.

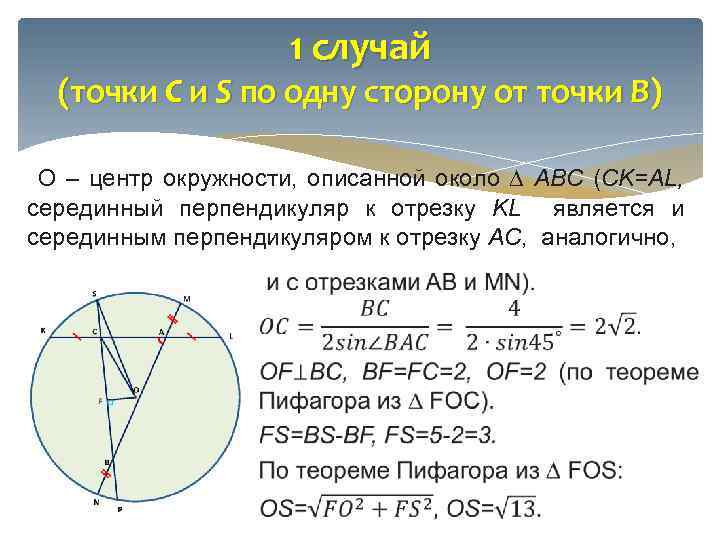1 случай (точки C и S по одну сторону от точки B) О – центр окружности, описанной около ∆ АВС (CK=AL, серединный перпендикуляр к отрезку KL является и серединным перпендикуляром к отрезку AC, аналогично,

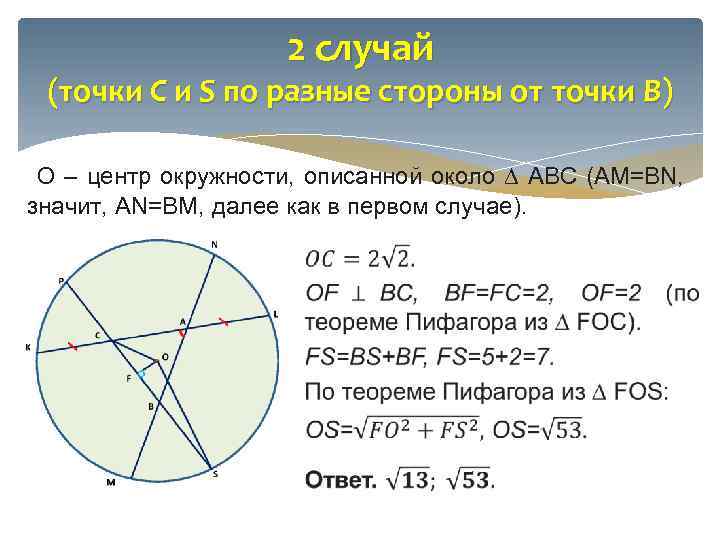2 случай (точки C и S по разные стороны от точки B) О – центр окружности, описанной около ∆ АВС (AM=BN, значит, AN=BM, далее как в первом случае).

Тренировочный вариант 17

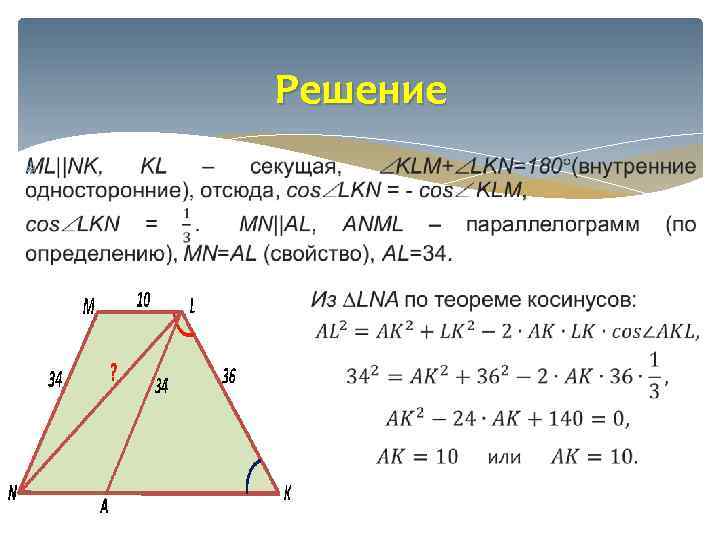Решение

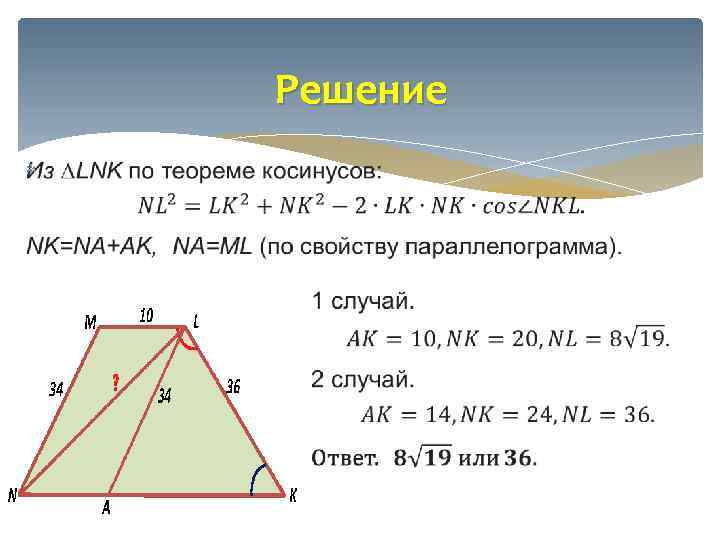Решение

Пробник 12

1 случай (угол B – острый)

2 случай (угол B – тупой)

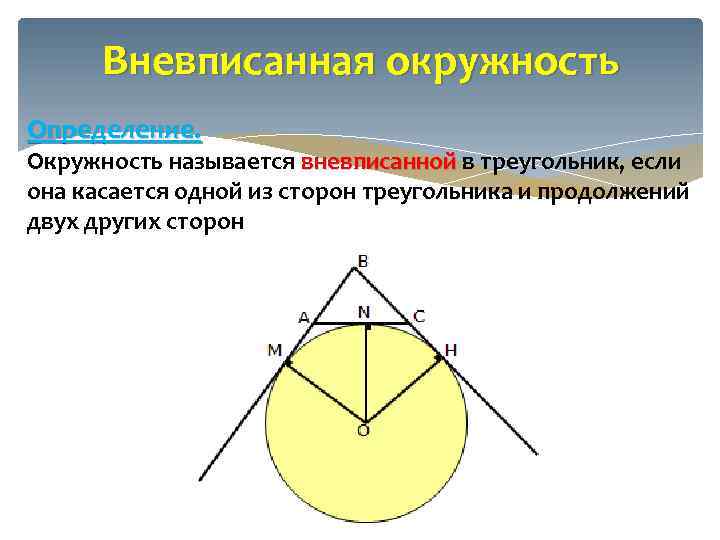Вневписанная окружность Определение. Окружность называется вневписанной в треугольник, если она касается одной из сторон треугольника и продолжений двух других сторон

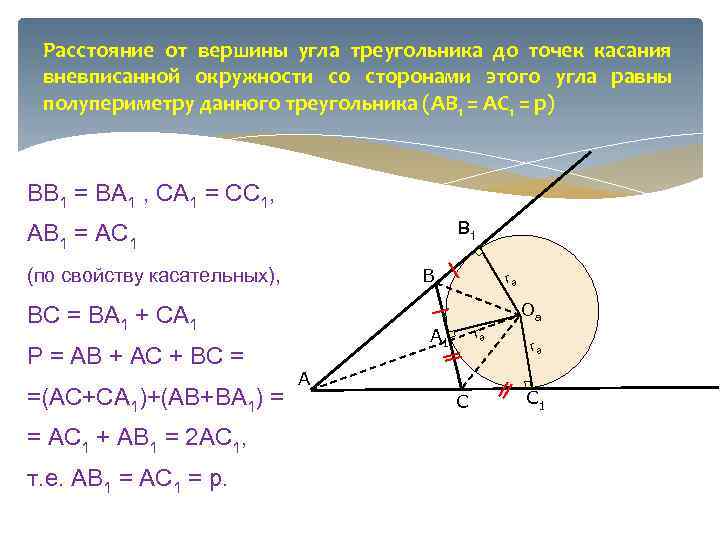Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника (АВ 1 = АС 1 = p) ВВ 1 = ВА 1 , СА 1 = СС 1, В 1 АВ 1 = АС 1 (по свойству касательных), В BC = ВА 1 + СА 1 P = AB + AC + BC = =(AC+СА 1)+(AB+ВА 1) = = AC 1 + AB 1 = 2 AC 1, т. е. АВ 1 = АС 1 = p. ra Оа А 1 ra А С ra С 1

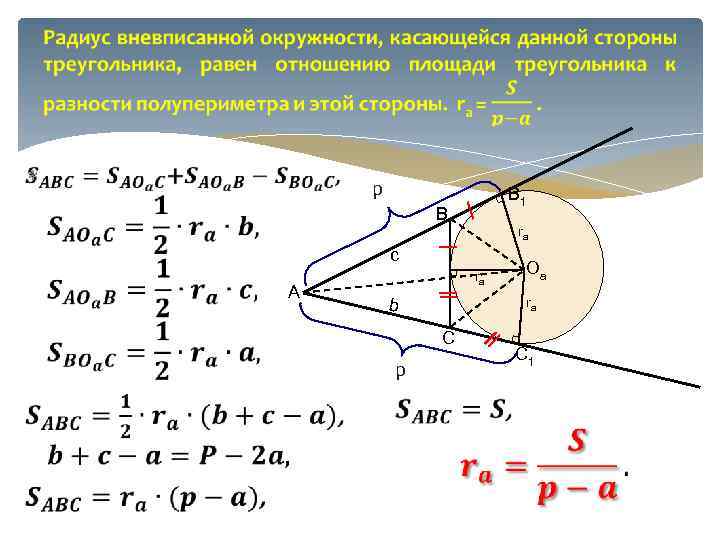p В 1 В ra c А ra b ra С p Оа С 1

Пробник 11 11. Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон. Радиусы вневписанных окружностей прямоугольного треугольника равны 5 и 20. Найдите площадь треугольника.

Три способа решения задачи 11

1 способ МЕТОД ПОДОБИЙ

1 случай (касание катетов)

2 случай (касание катета и гипотенузы)

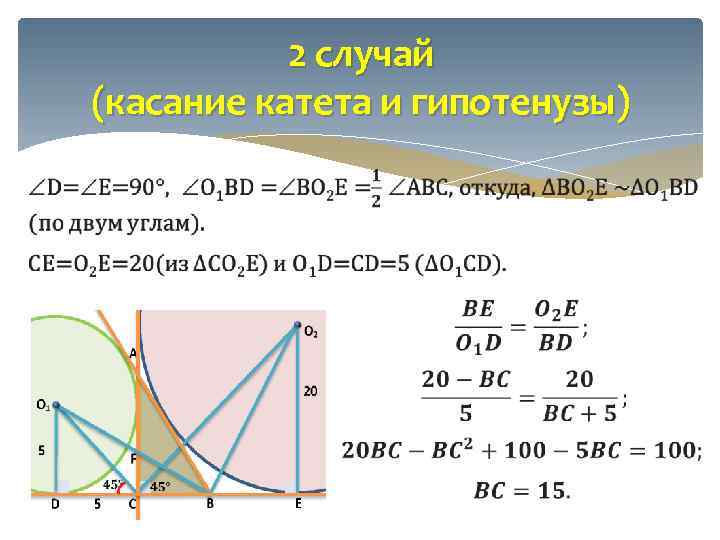2 случай (касание катета и гипотенузы) K= M=90 , O 1 AM = O 2 AK (вертикальные, точки O 1, А и O 2 лежат на одной прямой), откуда, ∆АO 2 K ~∆AO 1 M (по двум углам). CK=CE=20(свойство касательных) и O 1 M=CM=5 (∆O 1 CM).

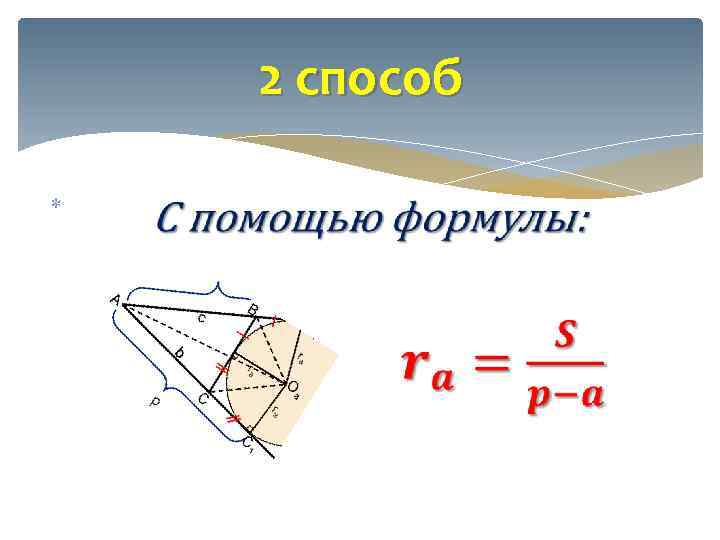2 способ

1 случай (касание катетов)

2 случай (касание катета и гипотенузы)

Тренировочный 18 12. Две окружности касаются внешним образом. Прямая касается первой окружности в точке M и пересекает вторую окружность в точках A и B. Найдите радиус первой окружности, если известно, что AB = 12, MB = 6, а радиус второй окружности равен 10.

Тренировочный 19 13. Диагонали АС и BD трапеции ABCD пересекаются в точке Е. Найдите площадь трапеции, если площадь треугольника AED равна 9, а точка Е делит одну из диагоналей в отношении 1: 3.

Интернет - ресурсы webmath. exponenta. ru/mege/Index. html alexlarin. net www. egetrener. ru reshuege. ru live. mephist. ru/show/mathege-solutions/C 4 mathege. ru – Открытый банк задач bankege. ru