Методика изучения устных вычислительных приемов сложения и вычитания

Методика изучения устных вычислительных приемов сложения и вычитания

В методике различают устные и письменные приемы вычисления. К устным относят все приемы в пределах 100, а также сводящиеся к ним приемы за пределами 100.

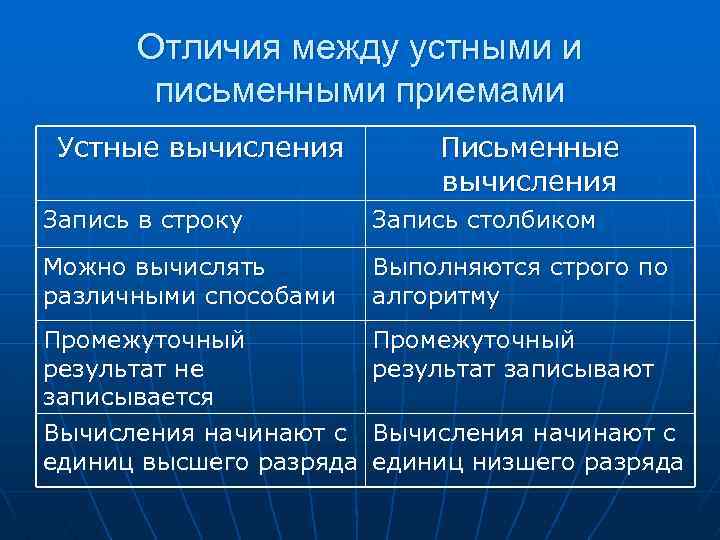Отличия между устными и письменными приемами Устные вычисления Письменные вычисления Запись в строку Запись столбиком Можно вычислять различными способами Выполняются строго по алгоритму Промежуточный результат не записывается Вычисления начинают с единиц высшего разряда Промежуточный результат записывают Вычисления начинают с единиц низшего разряда

Методические особенности формирования умений устных вычислений n n Последовательность рассмотрения вычислительных приемов определяется целями обучения и логикой построения курса. Основным способом введения вычислительного приема является показ образца действия, который в некоторых случаях разъясняется на предметном уровне, а затем закрепляется при выполнении упражнений

n Изучение каждого свойства (или правила) строится примерно по одному плану: сначала, используя наглядные пособия, надо раскрыть суть самого свойства, затем научить детей применять его при выполнении тренировочных упражнений, и затем, научить, пользуясь знанием свойства, находить рациональные приемы вычислений

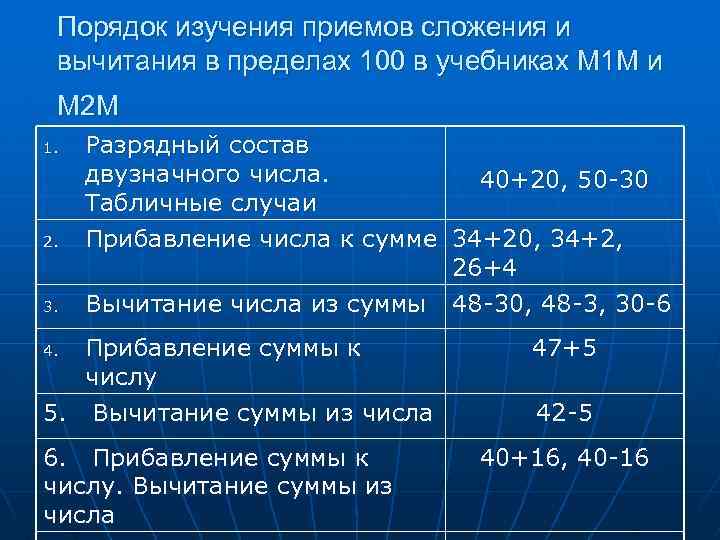Порядок изучения приемов сложения и вычитания в пределах 100 в учебниках М 1 М и М 2 М 1. 2. 3. Разрядный состав двузначного числа. 40+20, 50 -30 Табличные случаи Прибавление числа к сумме 34+20, 34+2, 26+4 Вычитание числа из суммы 48 -30, 48 -3, 30 -6 Прибавление суммы к числу 5. Вычитание суммы из числа 4. 6. Прибавление суммы к числу. Вычитание суммы из числа 47+5 42 -5 40+16, 40 -16

Для овладения вычислительными приемами учащиеся должны знать: n нумерацию чисел (разрядный состав числа) n таблицу сложения и вычитания в пределах 10 n свойства действий сложения и вычитания: ü переместительное свойство сложения; ü прибавление и вычитание числа из суммы; ü прибавление и вычитание суммы из числа. Навыки устных вычислений формируются в процессе выполнения разнообразных упражнений. Рассмотрим их основные виды.

1. Нахождение значений математических выражений Основное назначение таких упражнений – выработать твердые вычислительные навыки. Эти упражнения имеют много вариантов. n числовые выражения и выражения с переменной n выражения предлагаются в разной словесной форме: 100 -9 n выражения могут включать одно или несколько действий, скобки; иметь разную словесную формулировку 90 -42: 3

выражения могут быть заданы в разной области чисел: с однозначными числами (7 -4), с двузначными (72 -48), с трехзначными (720 -480), с величинами (2 м-15 см). Как правило приемы устных вычислений должны сводиться к действиям над числами в пределах 100. Например: 7200 -4800 (72 сот. -48 сот. ) n выражения можно задать в форме примера, таблицы, занимательных фигур. n

2. Сравнение математических выражений Главная роль таких упражненийспособствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах и неравенствах. n сравнить выражения: 6+4 и 4+6, 20+7 и 20+5,

Выбор знака отношения может быть выполнен либо на основе нахождения значений данных выражений, либо на основе применения знаний: переместительного свойства сложения (6+4=4+6); изменения результата действия в зависимости от изменения одного из компонентов (20+7>20+5). n закончить запись: 48+(2+10)=(48+…)+… n сравнение выражений с переменной: а-17 и а-12.

3. Решение уравнений Назначение таких упражнений-выработать умение решать уравнения, усвоить связи между компонентами и результатами действий, способствовать выработке вычислительных навыков. Уравнения можно предлагать в разных формах: n решите уравнение 24 -х=3; n из какого числа надо вычесть 18, чтобы получить 40? n найдите неизвестное число: 73 -х=73 -18; n я задумала число, прибавила к нему 8 и получила 83. Какое число я задумала?

4. Решение задач Для устной работы предлагаются и простые, и составные задачи. Эти упражнения включаются с целью выработки умений решать задачи, они помогают усвоению теоретических знаний и развитию вычислительных навыков. Чтобы навыки устных вычислений постоянно совершенствовались, необходимо установить правильное соотношение устных и письменных приемов: вычислять письменно только тогда, когда устно вычислить трудно.

Задания для устного счета предлагаются детям так, чтобы они воспринимали их либо зрительно, либо на слух, либо и зрительно, и на слух. Игры для устного счета: «Молчанка» , «Круговые примеры» , «Лабиринт» , «Магический квадрат» … Математические диктанты. Проверка проводится или на уроке, выявляются ошибки, или после урока, тогда работа каждого ученика оценивается.