Методическая разработка Поляковой Е. А. МОУ «Гимназия № 22 г. Белгорода»
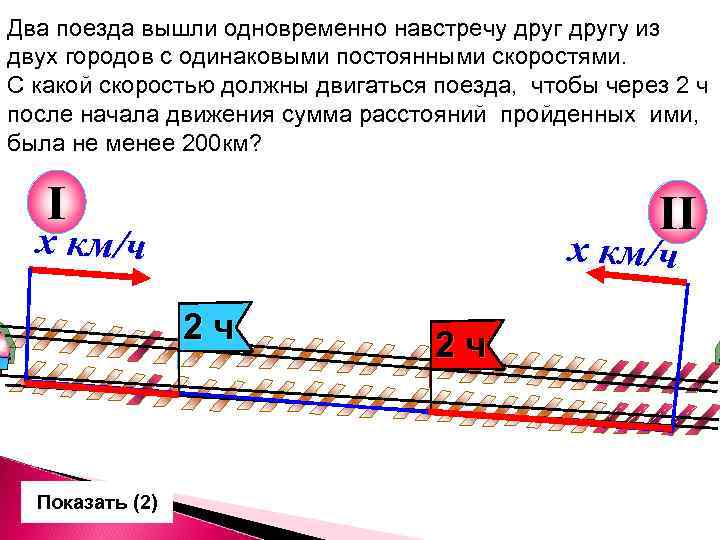
Два поезда вышли одновременно навстречу другу из двух городов с одинаковыми постоянными скоростями. С какой скоростью должны двигаться поезда, чтобы через 2 ч после начала движения сумма расстояний пройденных ими, была не менее 200 км? I II х км/ч 2 ч Показать (2) 2 ч
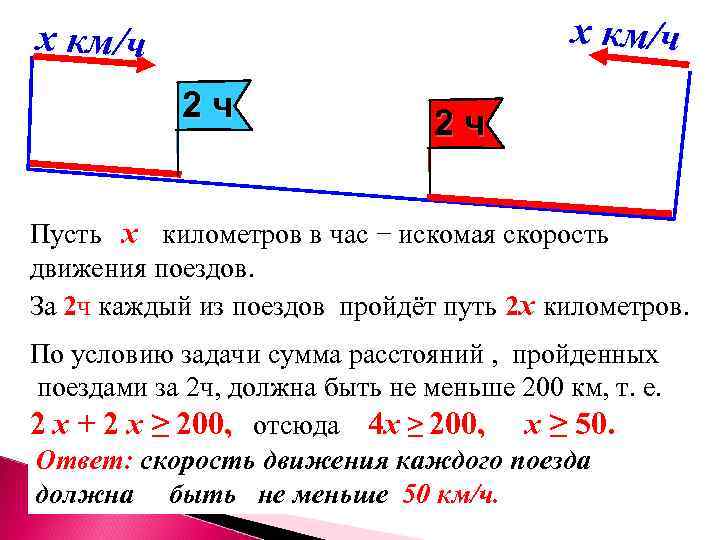
х км/ч 2 ч 2 ч Пусть х километров в час − искомая скорость движения поездов. За 2 ч каждый из поездов пройдёт путь 2 х километров. По условию задачи сумма расстояний , пройденных поездами за 2 ч, должна быть не меньше 200 км, т. е. 2 х + 2 х ≥ 200, отсюда 4 х ≥ 200, х ≥ 50. Ответ: скорость движения каждого поезда должна быть не меньше 50 км/ч.
В неравенстве 4 х ≥ 200 буквой х обозначено неизвестное число. Это пример неравенства первой степени с одним неизвестным. Неравенствами первой степени с одним неизвестным называются неравенства вида: kх > b, kx < b, kх ≥ b, kx ≤ b, где k и b − заданные числа, х − неизвестное. Другое название - линейное неравенство
Многие неравенства сводятся к линейным, например: Неизвестное число в неравенстве может быть обозначено любой буквой, например, в неравенствах
Неизвестное число в неравенстве может быть обозначено любой буквой, например, в неравенствах неизвестные обозначены соответственно буквами y, t, a. Выражения, стоящие слева и справа от знака неравенства, называют соответственно левой и правой частями неравенства. Каждое слагаемое левой и правой частей неравенства называют членом неравенства.
Назовите левую часть неравенства Назовите правую часть неравенства
Если в неравенство подставить а = 10, а = 4, то получатся верные числовые неравенства : 2∙ (5 − 2 ∙ 10) < 3 ∙ 10 + 2 ∙ (5 − 3 ∙ 10); 2∙ (5 − 2 ∙ 4) < 3 ∙ 4 + 2 ∙ (5 − 3 ∙ 4). Каждое из чисел 10, 4 называют неравенства решением
Решением неравенства с одним неизвестным называется такое значение переменной, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство − это значит, найти все его решения или установить, что их нет. Из чисел 7; 5; 2; 1, 5; 0; − 2 выбрать те, которые являются решениями неравенства : 1) 2 х − 3 ≥ 1; 2) 4 ─ х < 3; 3) 4 (х− 1) < − 2; 4) 2 (1 − х ) ≥ − 1;
Блиц-опрос 1) ─ 5 х < 0, 2) 4 х > 0, Решить неравенство : ______________ 3) ─ 0, 5 х ² ─ 1 < 0, 4) ( х ─ 3 ) ² < 0, ____________________________ 5) ( х + 2 ) ² > 0, ______________________
При решении неравенств используются следующие свойства: Свойство 1. Любой член неравенства можно перенести из одной части неравенства в другую, изменив знак этого члена на противоположный; при этом знак неравенства (знак сравнения) не меняется. Свойство 2. Обе части неравенства можно умножить или разделить на одно и то же, не равное нулю число; если это число положительно, то знак сравнения не меняется, а если это число отрицательно, то знак сравнения меняется на противоположный.
Скачать презентацию Методическая разработка Поляковой Е А МОУ Гимназия
Неравенства с одним неизвестным.ppt