МЕТОДИ СОРТУВАННЯ Лекція з курсу Структури даних Час

МЕТОДИ СОРТУВАННЯ Лекція з курсу «Структури даних» Час – 2 год

План • Сортування вибором • Сортування вставкою та сортування злиттям. • Сортування обміном і шейкерне сортування. • Сортування Шелла • Швидке сортування (сортування Хоара) • Турнірне сортування • Пірамідальне сортування

Упорядкування елементів множини в зростаючому або спадному порядку називається сортуванням. З упорядкованими елементами простіше працювати, ніж з довільно розташованими: легше знайти необхідні елементи, виключити, вставити нові. Сортування застосовується при організації наборів даних на зовнішніх носіях, при створенні бібліотек, каталогів, баз даних і т. д.

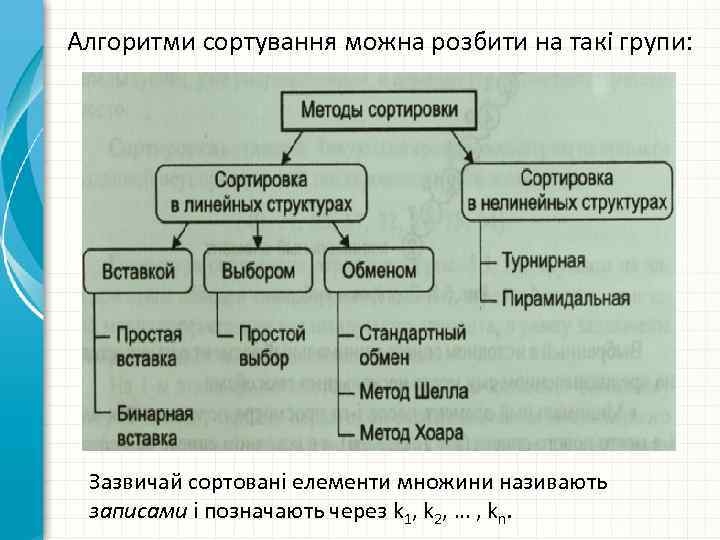Алгоритми сортування можна розбити на такі групи: Зазвичай сортовані елементи множини називають записами і позначають через k 1, k 2, … , kn.

Сортування вибором

Сортування вибором полягає в тому, що спочатку в невпорядкованому списку вибирається і відокремлюється від інших найменший елемент. Після цього вихідний список виявляється зміненим. Змінений список приймається за вихідний і процес продовжується до тих пір, поки всі елементи не будуть вибрані. Очевидно, що вибрані елементи утворюють упорядкований список.

Наприклад, потрібно знайти мінімальний елемент списку {5, 11, 6, 4, 9, 2, 15, 7}. Процес вибору зображений на рис. 2, де в кожному рядку виписані порівнювані пари. Можливі елементи з меншою вагою обведені гуртком. Нескладно побачити, що кількість порівнянь відповідає на малюнку числу рядків, а число переміщень - кількості змін обраного елемента.

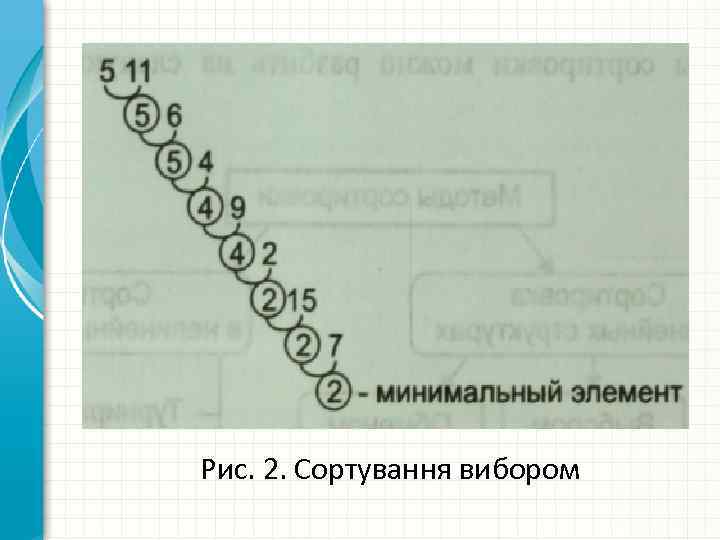Рис. 2. Сортування вибором

Обраний у вихідному списку мінімальний елемент розміщується на призначеному йому місці декількома способами. • Мінімальний елемент після i-го перегляду переміщається на і-е місце нового списку (і = 1, 2, . . . , n), а у вихідному списку на місце обраного елемента записується якесь дуже велике число, що перевершує за величиною будь елемент списку. • Мінімальний елемент записується на і-е місце вихідного списку (і = 1, 2, . . . , n), а елемент з i-го місця-на місце обраного. При цьому очевидно, що вже впорядковані елементи виключаються з подальшої сортування, тому довжина списку , який бере участь в кожному наступному перегляді буде на один елемент менше попереднього. • Обраний мінімальний елемент, як і в попередньому випадку, переміщається на i-е місце заданого списку, а щоб це i-е місце звільнилося для запису чергового мінімального елемента, ліву від обраного елемента частину списку переміщається вправо на одну позицію так, щоб заповнилося місце , займане до цього вибраним елементом.

Сортування вставкою та сортування злиттям

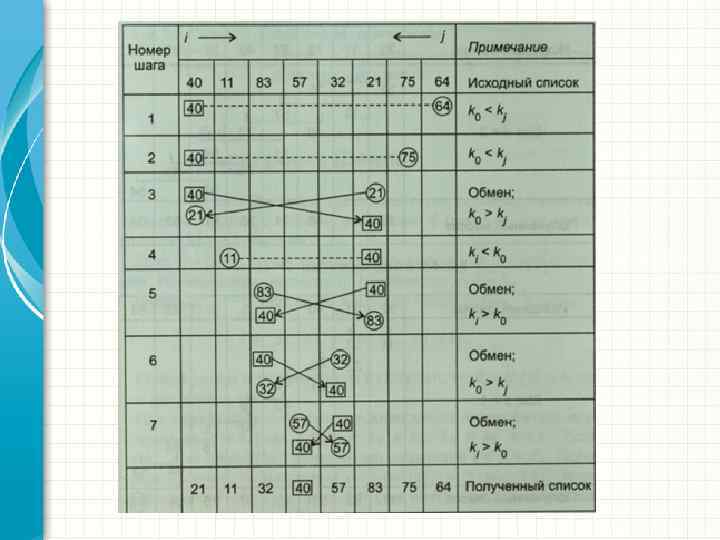
У цьому методі з невпорядкованої послідовності елементів вибирається по черзі кожен елемент, порівнюється з попереднім, вже впорядкованим, і поміщається на відповідне місце. Сортування вставкою. Таке сортування розглянемо на прикладі заданої невпорядкованою послідовності елементів: {40, 11, 83, 57, 32, 21, 75, 64}. Процедура сортування відображена на рис. 3, де колом на кожному етапі обведений аналізований елемент, стрілкою зверху зазначено місце переміщення аналізованого елемента, в рамку укладені впорядковані частини послідовності.

На 1 -му етапі порівнюються два початкових елемента. Оскільки другий елемент менше першого, він переміщається на місце першого елемента, який зсувається вправо на одну позицію. Інша частина послідовності залишається без зміни. На 2 -му етапі з невпорядкованою послідовності вибирається елемент і порівнюється з двома впорядкованими раніше елементами. Так як він більше попередніх, то залишається на місці. Потім аналізуються четвертий, п'ятий і наступні елементи до тих пір, поки весь список не буде впорядкованим, що має місце на останньому 7 -му етапі.

Рис. 3. Сортування вставкою

. Сортування злиттям. Різновидом сортування вставкою є метод фон Неймана, або сортування злиттям. Ідея методу полягає в наступному: спочатку аналізуються перші елементи обох впорядкованих масивів. Менший елемент переписується в новий масив. Той елемент, що залишився послідовно порівнюється з елементами з іншого масиву. У новий масив після кожного порівняння потрапляє менший елемент. Процес триває до вичерпання елементів одного з масивів. Потім залишок іншого масиву дописується в новий масив. Отриманий новий масив впорядкований таким же чином, як вихідні.

Нехай є два відсортованих в порядку зростання масиви p[1], p[2], …, p[n] і q[1], q[2], …, q[n] та є пустий масив r[1], r[2], . . . , r[2 n], який ми хочемо заповнити значеннями масивів p та q в порядку зростання. Для злиття виконуються наступні дії: порівнюються p[1] та q[1] і менше із значень записується в r[1]. Припустимо, що це значення р[1]. Тоді р[2] порівнюється з q[1] і менше із значень заноситься в r[2]. Припустимо, що це значення q[1]. Тоді на наступному кроці порівнюються значення р [2] та q [2] і т. д. , поки ми не досягнемо закінчення одного з масивів. Тоді залишок іншого масиву просто дописується в «хвіст» масиву r.

.

Сортування обміном і шейкерне сортування

Сортування обміном ( «бульбашкою). Це метод, в якому елементи списку послідовно порівнюються між собою і міняються місцями в тому випадку, якщо попередній елемент більше наступного. Потрібно, наприклад, провести сортування списку методом стандартного обміну, або методом «бульбашки» : {40, 11, 83, 57, 32, 21, 75, 64}. Позначимо квадратними дужками із стрілками обмінювані елементи, а без стрілок – порівнювані елементи. Перший етап сортування зображений на рис. 5, а другий етап - на рис. 6.

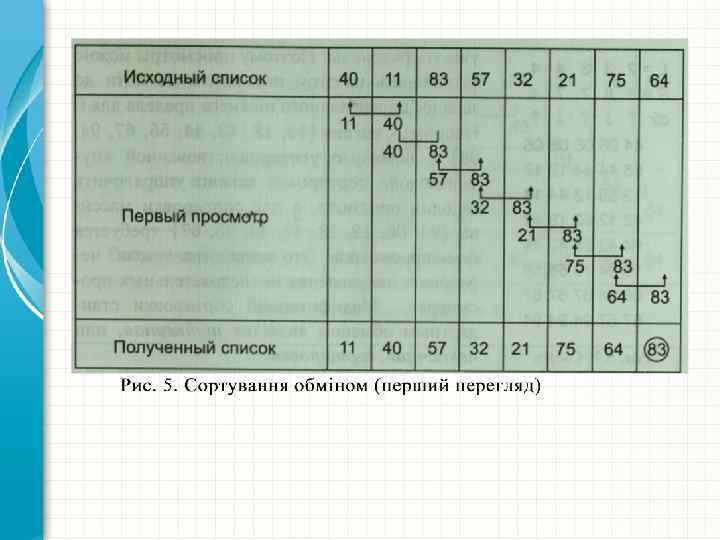
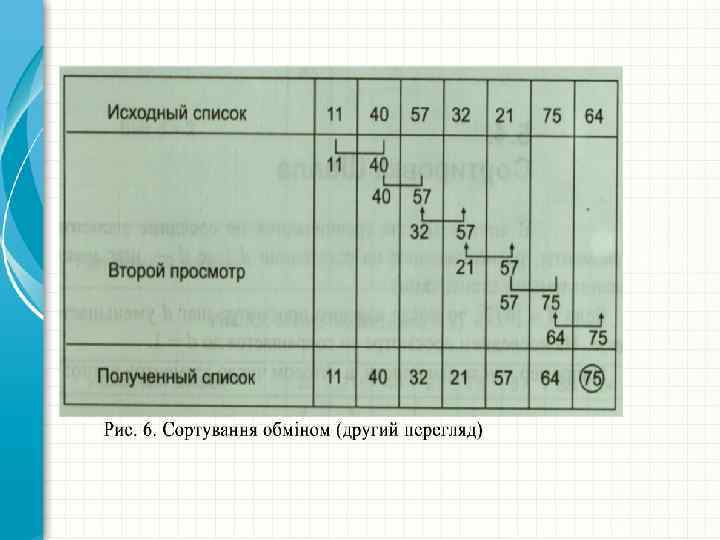
Нескладно побачити, що після кожного перегляду списку всі елементи, починаючи з останнього, займають свої остаточні позиції, тому їх не слід перевіряти при наступних переглядах. Кожен наступний перегляд виключає чергову позицію зі знайденим максимальним елементом, тим самим скорочуючи список. Після першого перегляду в останній позиції опинився найбільший елемент, рівний 83 (виключаємо його з подальшого розгляду). Другий перегляд виявляє максимальний елемент, рівний 75 і т. д.

Процес сортування продовжується до тих пір, поки не будуть сформовані всі елементи кінцевого списку або не виконається умова Айверсона. Умова Айверсона: якщо в ході сортування при порівнянні елементів не було зроблено жодної перестановки, то множина вважається впорядкованою (умова Айверсона виконується тільки при кроці (d = 1)

Шейкерне сортування. Очевидний прийом поліпшення алгоритму стандартного обміну - запам'ятовувати, були чи не були перестановки в процесі деякого проходу. Якщо в останньому проході перестановок не було, то алгоритм можна закінчувати. Це поліпшення, однак, можна знову ж таки поліпшити, якщо запам'ятовувати не тільки сам факт, що обмін мав місце, але і положення (індекс) останнього обміну. Ясно, що всі пари сусідніх елементів вище цього індексу k вже впорядковані. Тому перегляди можна закінчувати на цьому індексі, а не йти до заздалегідь визначеної нижньої межі для i.

Наприклад, масив {12, 18, 42, 44, 55, 67, 94, 06} за допомогою вдосконаленого «бульбашкового» сортування можна впорядкувати за один перегляд, а для сортування масиву {94, 06, 12, 18, 42, 44, 55, 67} потрібно сім переглядів. Це наводить на думку: чергувати напрямок послідовних переглядів. Модифікацією сортування стандартним обміном є шейкерне, або човникове, сортування. На рис. 7 наведено схему шейкерного сортування.

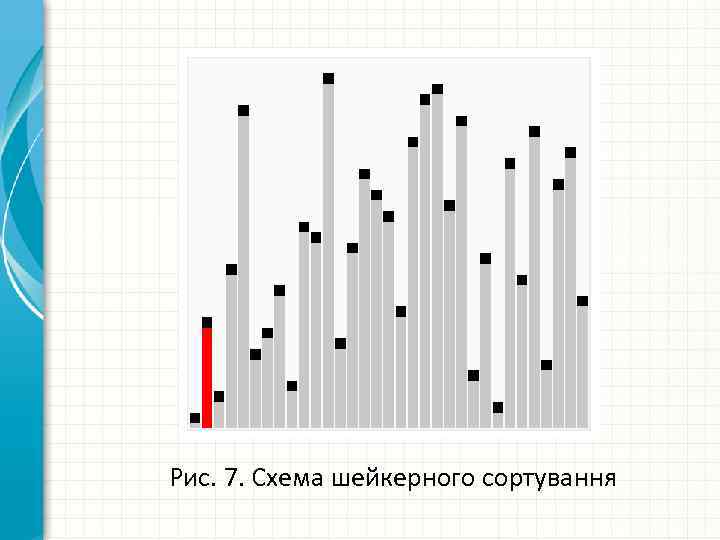Рис. 7. Схема шейкерного сортування

Сортування Шелла

У методі Шелла порівнюються не сусідні елементи, а елементи, розташовані на відстані d (де d - крок між порівнюваними елементами). Якщо d=[n/2], то після кожного перегляду крок d зменшується вдвічі. На останньому перегляді він скорочується до d=1.

Рис. 8. Метод Шелла (d=4)

Рис. 9. Метод Шелла (d=2)

Рис. 10. Метод Шелла (d=1)

Швидке сортування (сортування Хоара)

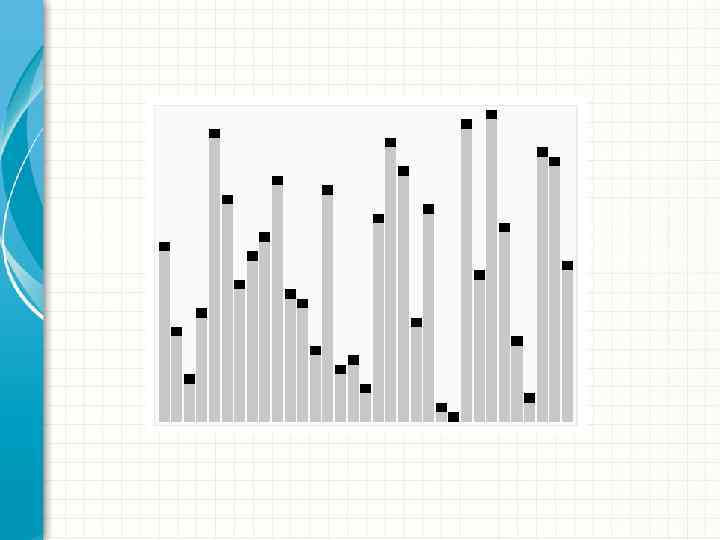
У методі швидкого сортування фіксується який-небудь ключ (базовий), щодо якого всі елементи з більшою вагою переміщуються праворуч, а з меншою - ліворуч. При цьому весь список елементів ділиться щодо базового ключа на дві частини. Для кожної частини процес повторюється. Пояснимо метод на прикладі. На рис. 11 представлені етапи швидкого сортування Хоара. У першому рядку вказана вихідна послідовність.

На відміну від попередніх розглянутих сортувань вже на першому етапі мають місце два факти: поперше, базовий ключ k 0=40 зайняв своє постійне місце у сортованій послідовності, по-друге, всі елементи ліворуч від k 0 будуть менші нього, а праворуч - більші за нього. Таким чином, після закінчення першого етапу маємо: Вказана процедура сортування знову застосовується незалежно до лівої і правої частин.

Турнірне сортування

Елементи вихідної множини представляються листками дерева. Їх попарне порівняння дозволяє визначити мінімальний (максимальний) елемент. Метод турнірного сортування заснований на повторюваних пошуках найменшого ключа серед n елементів, серед решти n-1 елементів і т. д. Наприклад, зробивши n/2 порівнянь, можна визначити в кожній парі ключів найменший. За допомогою n/4 порівнянь - найменший з пари вже обраних найменших і т. д.

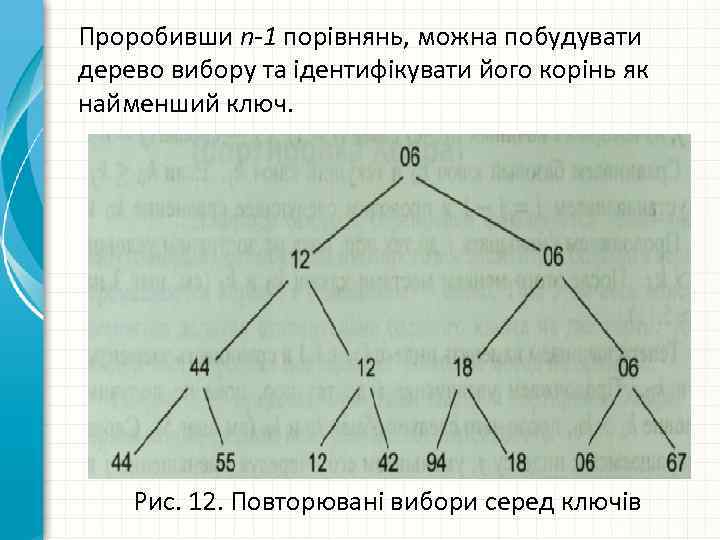Проробивши n-1 порівнянь, можна побудувати дерево вибору та ідентифікувати його корінь як найменший ключ. Рис. 12. Повторювані вибори серед ключів

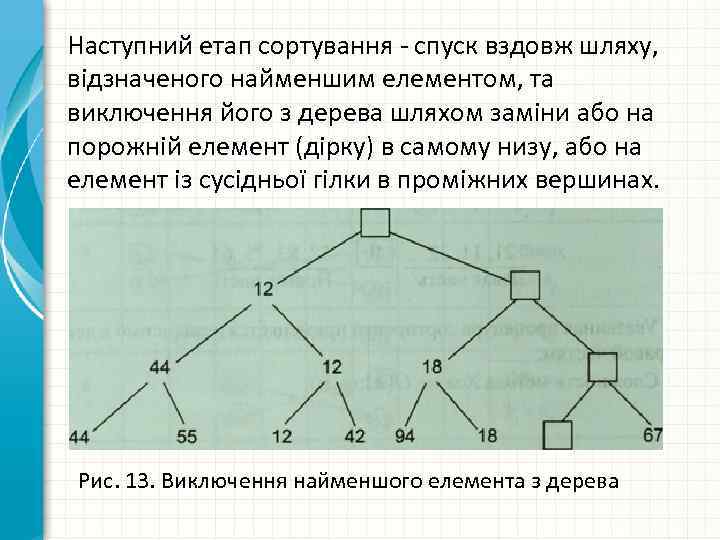Наступний етап сортування - спуск вздовж шляху, відзначеного найменшим елементом, та виключення його з дерева шляхом заміни або на порожній елемент (дірку) в самому низу, або на елемент із сусідньої гілки в проміжних вершинах. Рис. 13. Виключення найменшого елемента з дерева

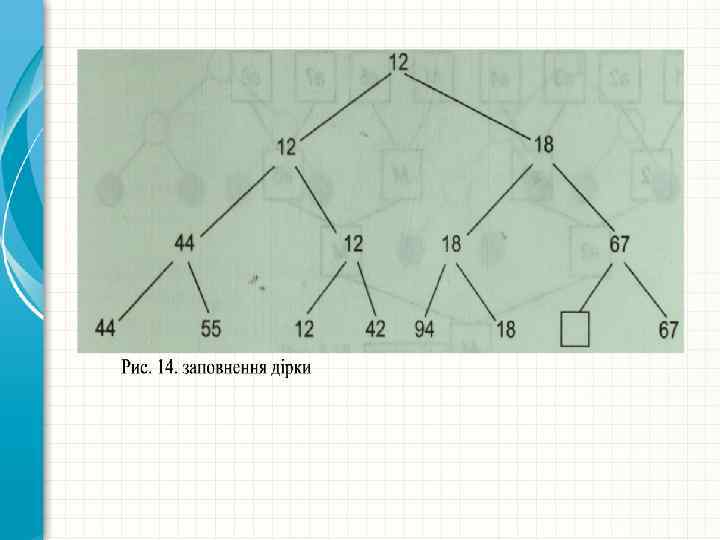
Елемент, що пересунувся в корінь дерева, знову буде найменшим (тепер уже другим) ключем (рис. 14), і його можна виключити. Після n таких кроків дерево стане порожнім (тобто в ньому залишаться одні дірки), і процес сортування закінчується. Свою назву турнірне сортування отримало тому, що воно використовується при проведенні змагань, турнірів та олімпіад.

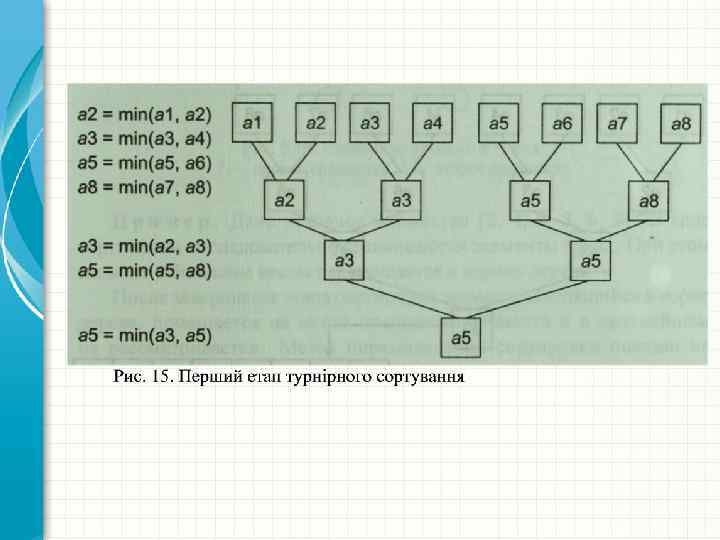
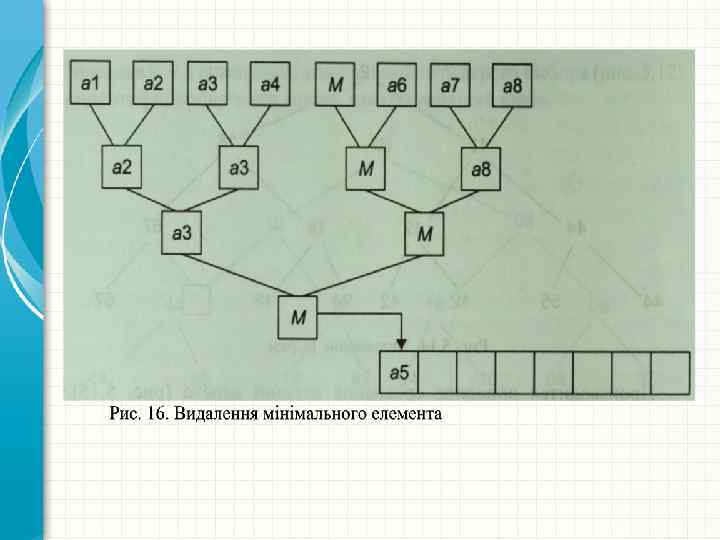
Приклад 1. Дана вихідна множина {а 1, а 2, а. З, а 4, а 5, а 6, а 7, а 8}. Виконати турнірне сортування Проводиться попарне порівняння вершин дерева (рис. 15). Знайдений мінімальний елемент замінюється спеціальним символом М і поміщається в результуючу множину (рис. 16).

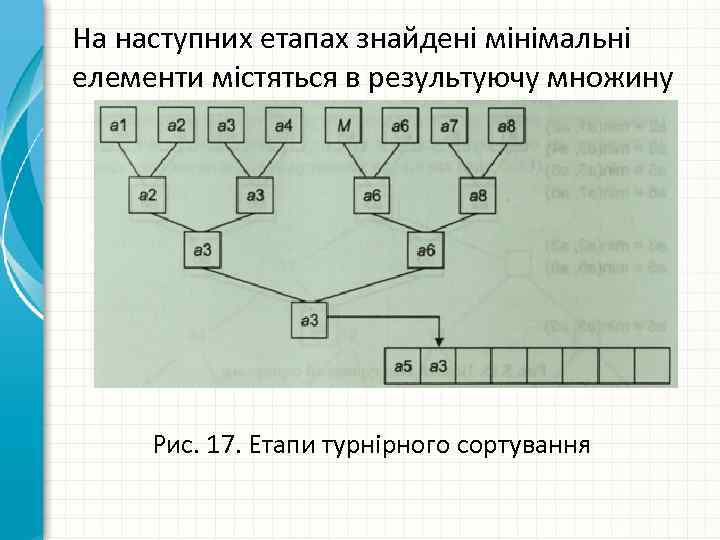На наступних етапах знайдені мінімальні елементи містяться в результуючу множину Рис. 17. Етапи турнірного сортування

Пірамідальне сортування

Даний тип сортування полягає в побудові пірамідального дерева, а саме бінарного дерева, що має три властивості: • у вершині кожної тріади розташовується елемент з більшою вагою; • листя бінарного дерева розташовуються або на одному рівні, або на двох сусідніх (рис. 18); • листя нижнього рівня розташовуються лівіше листя більш високого рівня.

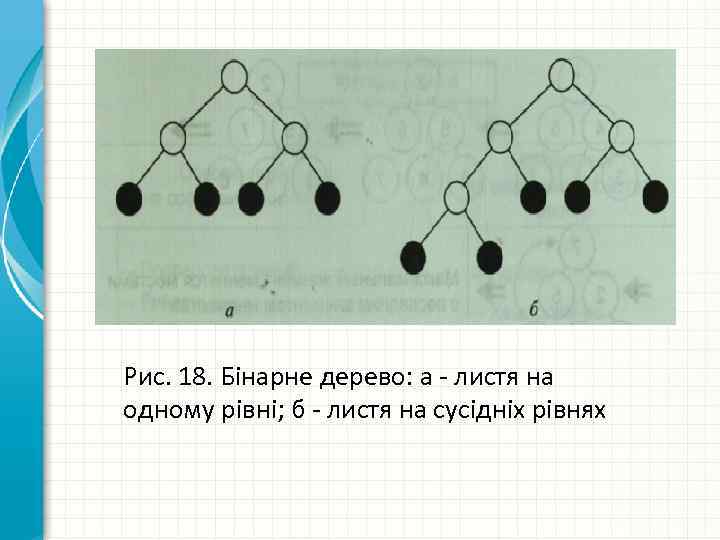Рис. 18. Бінарне дерево: а - листя на одному рівні; б - листя на сусідніх рівнях

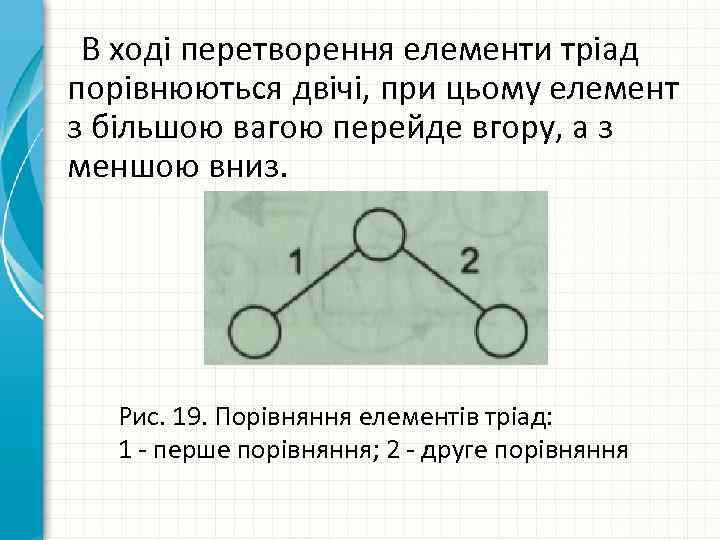В ході перетворення елементи тріад порівнюються двічі, при цьому елемент з більшою вагою перейде вгору, а з меншою вниз. Рис. 19. Порівняння елементів тріад: 1 - перше порівняння; 2 - друге порівняння

• Приклад. Дано вихідну множину {2, 4, 6, 3, 5, 7}. В ході сортування послідовно порівнюються елементи тріад. При цьому елемент з більшою вагою переміщається в корінь дерева. • Після завершення етапу сортування елемент, що знаходиться в корені дерева, поміщається на місце останнього елемента і надалі не розглядається. Метод пірамідального сортування зображений на рис. 20.

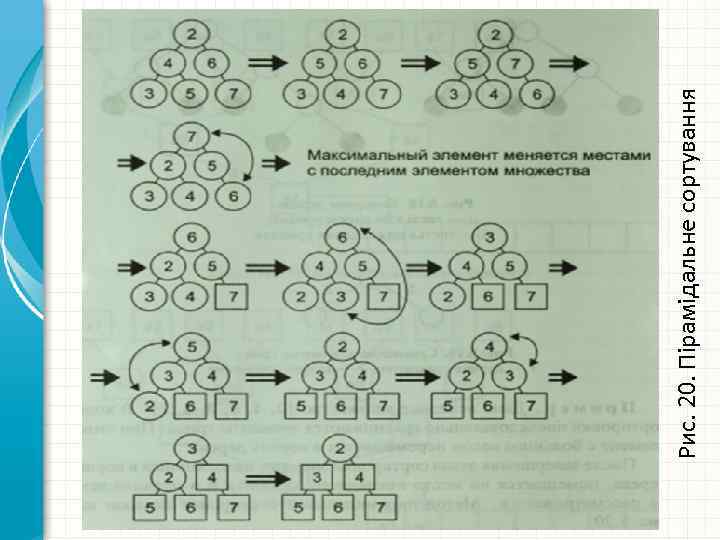Рис. 20. Пірамідальне сортування

Анімаційне порівняння алгоритмів сортування можна переглянути: http: //www. sorting-algorithms. com/

ПИТАННЯ?

ДЯКУЮ ЗА УВАГУ!!!