Metodi Quantitativi per Economia Finanza e Management Lezione

Metodi Quantitativi per Economia, Finanza e Management Lezione n° 8 L’utilizzo dell’analisi fattoriale nella costruzione di un modello di regressione lineare multipla

Analisi fattoriale Quante componenti considerare? 1. metodo degli autovalori >1 2. 3. rapporto tra numero di componenti e variabili (circa 1/3) percentuale di varianza spiegata (almeno 60%) 4. lo SCREE PLOT (plot di autovalore vs il numero di fattori) Se il plot mostra un “gomito” è plausibile ipotizzare l’esistenza di una struttura latente, se la forma è quasi rettilinea significa che i fattori sono solo una trasformazione delle variabili manifeste. I fattori rilevanti sono quelli al di sopra del gomito (a discrezione anche quello in corrispondenza del gomito). Se non ci sono fattori predominanti il criterio è inadatto.

Analisi fattoriale Quante componenti considerare? 5. Comunalità: - confronto tra le comunatità di più soluzioni - la quota di varianza spiegata di ciascuna variabile dalla soluzione scelta deve essere soddisfacente

Analisi fattoriale Come interpretarle? 1. rotazione delle componenti La rotazione ortogonale nello spazio dei fattori non influenza la validità del modello: sfruttiamo questa caratteristica per ottenere dei fattori più facilmente interpretabili. – – – 2. The Varimax method of rotation, suggested by Kaiser, has the purpose of minimizing the number of variables with high saturations (correlations) for each factor The Quartimax method attempts to minimize the number of factors tightly correlated to each variable The Equimax method is a cross between the Varimax and the Quartimax correlazioni tra componenti principali e variabili originarie

Esempi di Analisi Fattoriale di vecchi lavori di gruppo

Esempio Importanza dell’Informazione e modalità di acquisizione Obiettivo della ricerca è comprendere quali siano i principali mezzi informativi, il relativo indice di gradimento e quali siano gli argomenti di maggior interesse. Analisi fattoriale: Le variabili considerate sono i 14 parametri che influenzano la scelta del canale e quelli che influenzano la scelta relativa al tipo di fonte

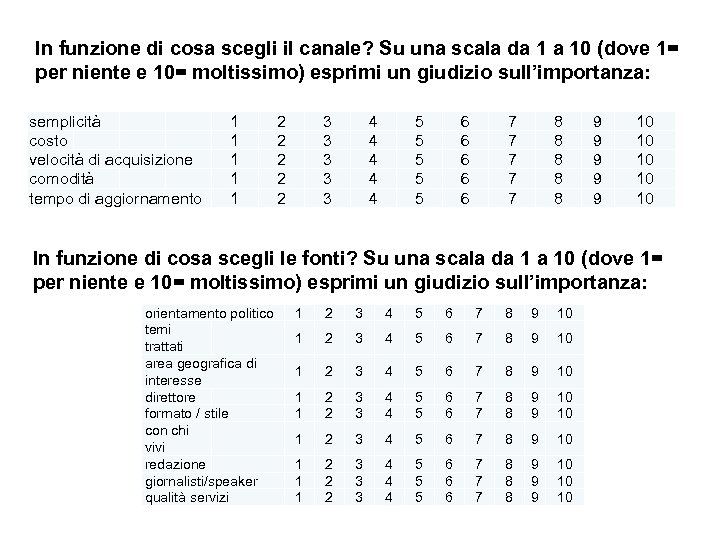In funzione di cosa scegli il canale? Su una scala da 1 a 10 (dove 1= per niente e 10= moltissimo) esprimi un giudizio sull’importanza: semplicità costo velocità di acquisizione comodità tempo di aggiornamento 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 10 10 10 In funzione di cosa scegli le fonti? Su una scala da 1 a 10 (dove 1= per niente e 10= moltissimo) esprimi un giudizio sull’importanza: orientamento politico temi trattati area geografica di interesse direttore formato / stile con chi vivi redazione giornalisti/speaker qualità servizi 1 2 3 4 5 6 7 8 9 10 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 1 2 3 4 5 6 7 8 9 10 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 10 10 10

Esempio Importanza dell’Informazione e modalità di acquisizione Le variabili considerate sono i parametri che influenzano la scelta del canale e quelli che influenzano la scelta relativa al tipo di fonte

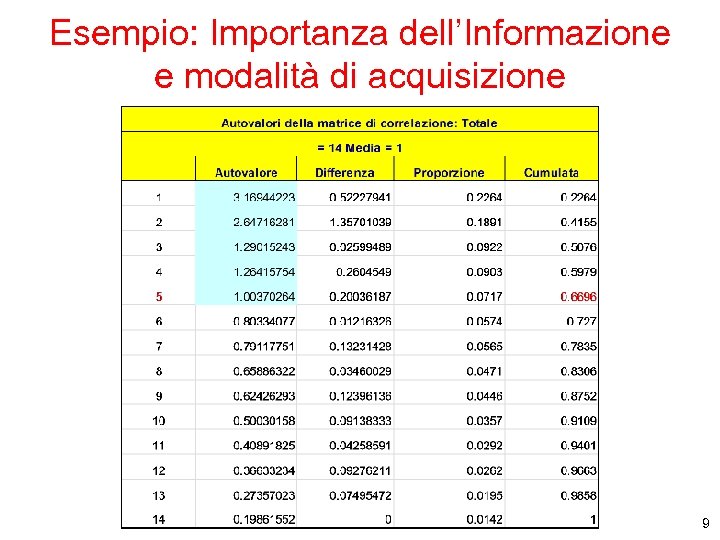Esempio: Importanza dell’Informazione e modalità di acquisizione 9

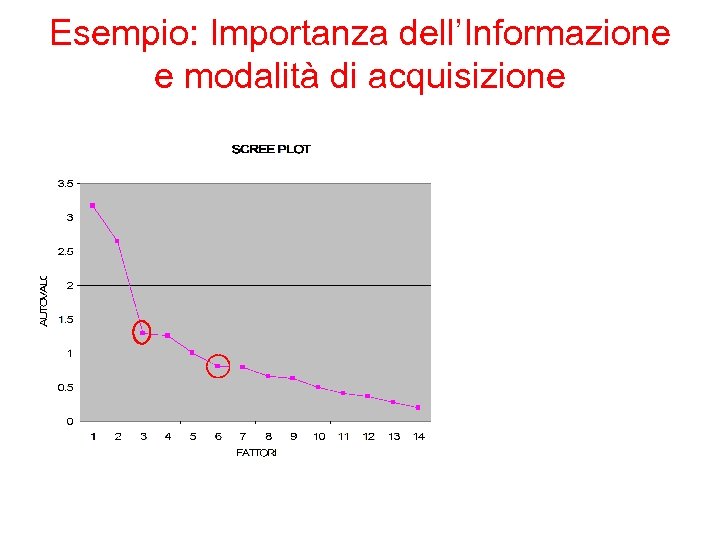Esempio: Importanza dell’Informazione e modalità di acquisizione

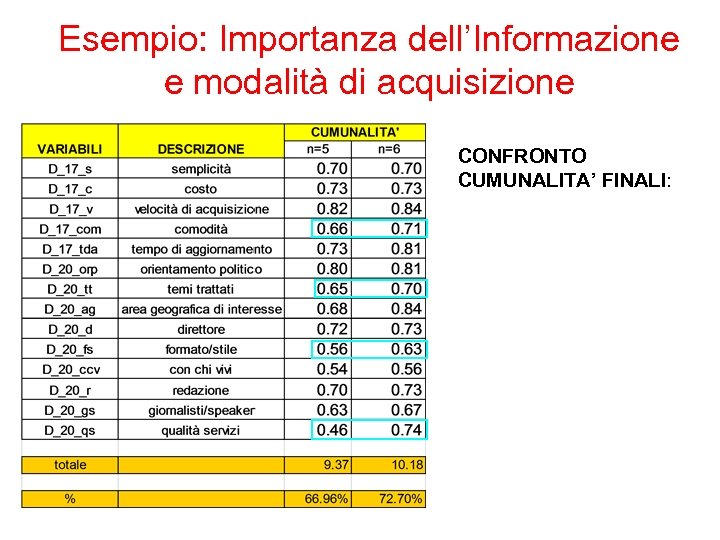Esempio: Importanza dell’Informazione e modalità di acquisizione CONFRONTO CUMUNALITA’ FINALI:

Esempio: Importanza dell’Informazione e modalità di acquisizione Schema fattoriale Factor 1 Factor 2 Factor 3 Factor 4 Factor 5 D_17_s semplicità 0. 56626 . . . 0. 46051 D_17_c costo 0. 35685 . 0. 65469 . 0. 3875 D_17_v velocità 0. 75292 . . D_17_com comodità 0. 68764 -0. 36206 . . . D_17_tda tempo di aggiornamento 0. 5326 -0. 43612 . . -0. 38524 D_20_orp orientamento politico . 0. 54298 . 0. 53024 . 0. 41299 . . 0. 53419 . D_20_tt temi trattati D_20_ag area geografica di interesse . . -0. 5248 . 0. 38026 D_20_d direttore . 0. 74874 . . . D_20_fs formato/stile 0. 38261 . . -0. 43544 . D_20_ccv con chi vivi . 0. 50515 . . . D_20_r redazione . 0. 72899 . . . D_20_gs giornalisti/speaker 0. 58604 0. 49902 . . . D_20_qs qualità servizi 0. 63683 . . I valori minori di 0. 35 non sono stampati. Lo schema fattoriale a 5 fattori, così come si presenta, è di difficile interpretazione; per questo risulta opportuno ruotare i fattori attraverso un apposito metodo (VARIMAX).

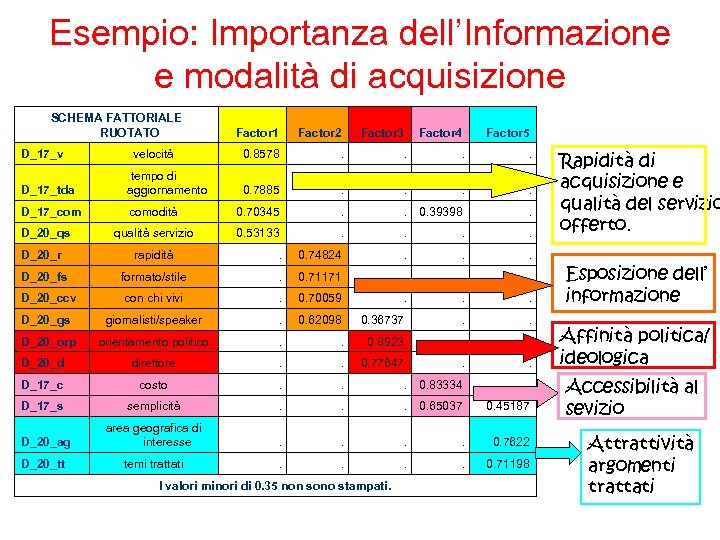Esempio: Importanza dell’Informazione e modalità di acquisizione SCHEMA FATTORIALE RUOTATO D_17_v velocità Factor 1 Factor 2 Factor 3 Factor 4 Factor 5 0. 8578 . . 0. 7885 . . D_17_tda tempo di aggiornamento D_17_com comodità 0. 70345 . . 0. 39398 . qualità servizio 0. 53133 . . D_20_qs D_20_r rapidità . 0. 74824 . . . D_20_fs formato/stile . 0. 71171 . . . D_20_ccv con chi vivi . 0. 70059 . . . D_20_gs giornalisti/speaker . 0. 62098 0. 36737 . . D_20_orp orientamento politico . . 0. 8923 . . D_20_d direttore . . 0. 77647 . . D_17_c costo . . . 0. 83334 . D_17_s semplicità . . . 0. 65037 0. 45187 D_20_ag area geografica di interesse . . 0. 7622 D_20_tt temi trattati . . 0. 71198 I valori minori di 0. 35 non sono stampati. Rapidità di acquisizione e qualità del servizio offerto. Esposizione dell’ informazione Affinità politica/ ideologica Accessibilità al sevizio Attrattività argomenti trattati

Coffee Consumption in Italy

Factor Analysis We ran a Factor Analysis on two numerical questions from the survey that we felt might have correlated variables: Q 15 (“What are you general coffee preferences? ”) and Q 16 (“If you drink your coffee outside (in a bar/coffee place) which are the main factors that, in general, influence your decision on where you drink your coffee? ”). • We used the Principal Components Method that was supposed to solve the multicollinearity problem among our variables and provide us with summarized number of variables/factors which are not correlated (standardized by definition, with mean 0, standard deviation 1) to better explain and understand the specific situation of coffee consumption. • This represents a preliminary phase for cluster analysis and regression analysis.

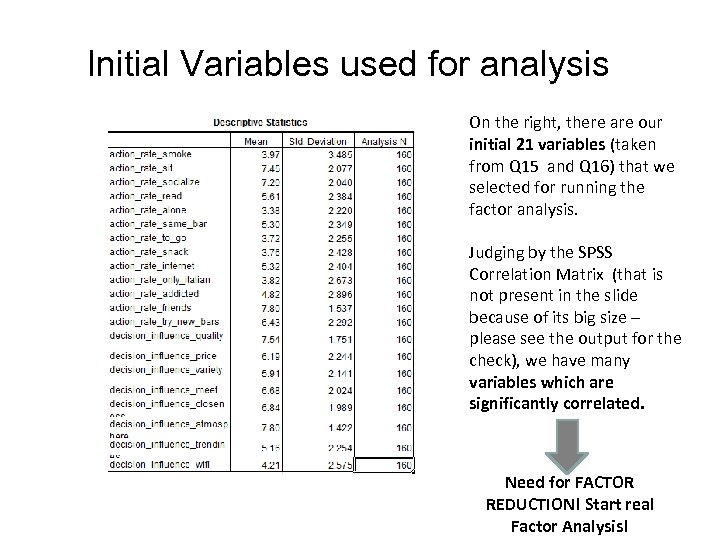Initial Variables used for analysis On the right, there are our initial 21 variables (taken from Q 15 and Q 16) that we selected for running the factor analysis. Judging by the SPSS Correlation Matrix (that is not present in the slide because of its big size – please see the output for the check), we have many variables which are significantly correlated. Need for FACTOR REDUCTION! Start real Factor Analysis!

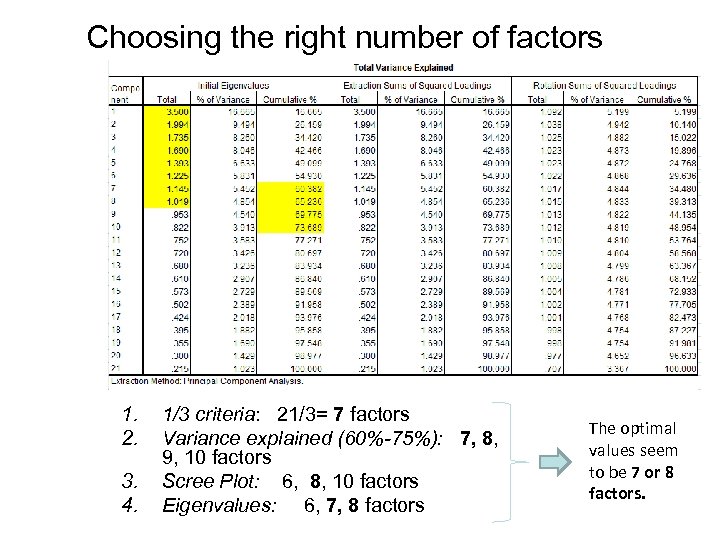Choosing the right number of factors 1. 2. 3. 4. 1/3 criteria: 21/3= 7 factors Variance explained (60%-75%): 7, 8, 9, 10 factors Scree Plot: 6, 8, 10 factors Eigenvalues: 6, 7, 8 factors The optimal values seem to be 7 or 8 factors.

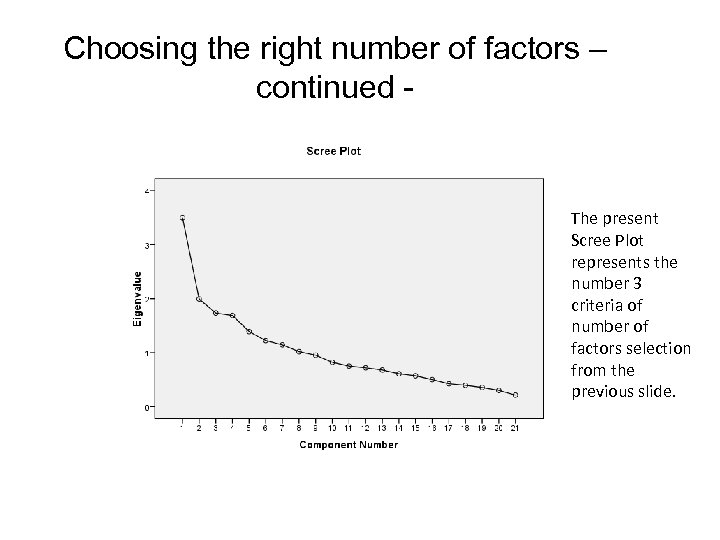Choosing the right number of factors – continued - The present Scree Plot represents the number 3 criteria of number of factors selection from the previous slide.

Factor Analysis with 8 Factors After analyzing the Communalities table, we identified one variable that is not properly explained by our 8 selected factors (0. 387 is not satisfying)! This variable is Price which we consider an important variable in our analysis! Decreasing the number of factors to 7, will not improve the explanatory power of the variables for the price! We decided to exclude the Price variable from this factor analysis and consider it as a separate factor (given its very high importance from our qualitative point view) in the future analysis: cluster & regression analysis.

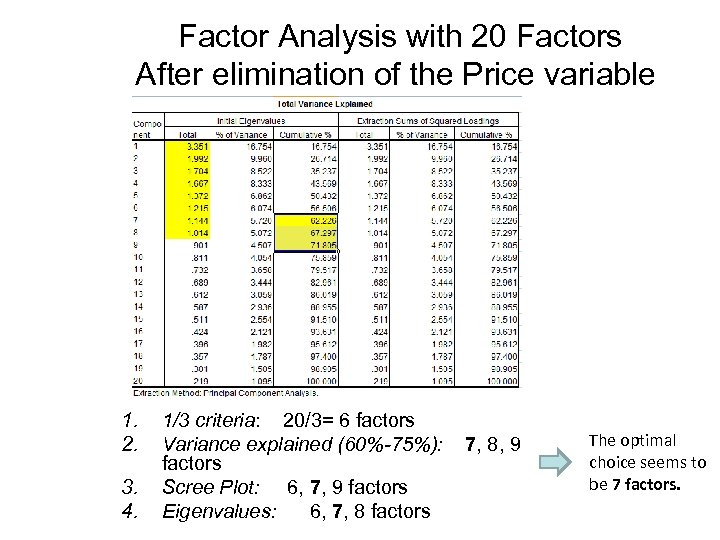Factor Analysis with 20 Factors After elimination of the Price variable 1. 2. 3. 4. 1/3 criteria: 20/3= 6 factors Variance explained (60%-75%): factors Scree Plot: 6, 7, 9 factors Eigenvalues: 6, 7, 8 factors 7, 8, 9 The optimal choice seems to be 7 factors.

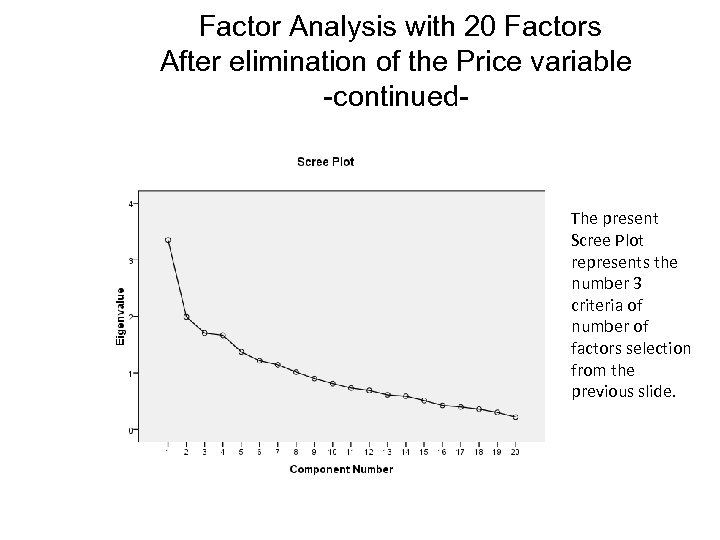Factor Analysis with 20 Factors After elimination of the Price variable -continued- The present Scree Plot represents the number 3 criteria of number of factors selection from the previous slide.

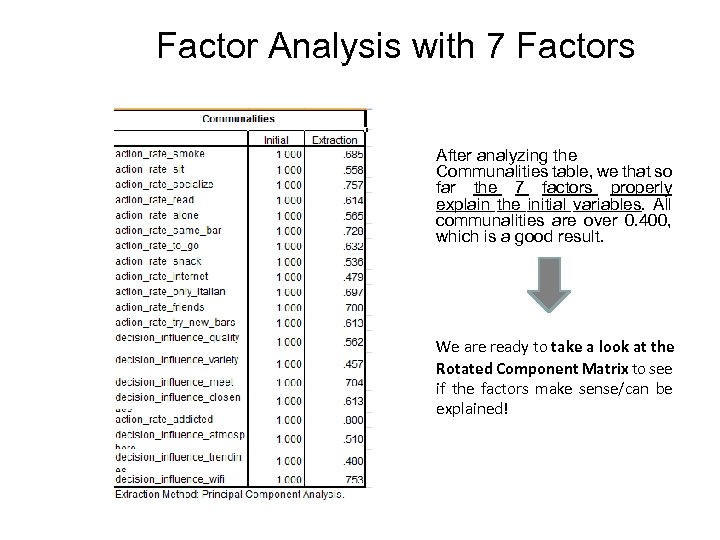Factor Analysis with 7 Factors After analyzing the Communalities table, we that so far the 7 factors properly explain the initial variables. All communalities are over 0. 400, which is a good result. We are ready to take a look at the Rotated Component Matrix to see if the factors make sense/can be explained!

Factors - explained • • • 1. 2. 3. 4. 5. 6. 7. The method used for rotation was Varimax. After closely analyzing the Rotated Component Matrix, we tried to give meaning to our 7 factors. The names of the respective factors are the following: Socialization factor Internet/ Trendiness factor Close meeting place factor Intellectual/ nonsmoking factor Familiarity factor Variety/To Go factor Traditionality & Addiction factor

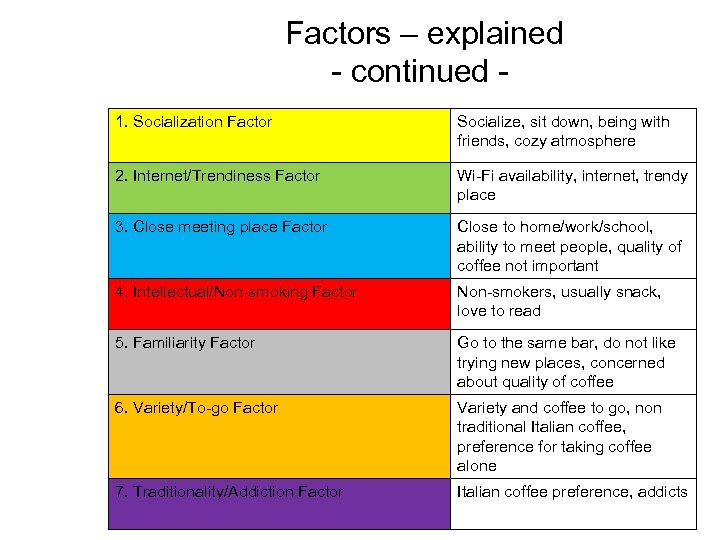Factors – explained - continued 1. Socialization Factor Socialize, sit down, being with friends, cozy atmosphere 2. Internet/Trendiness Factor Wi-Fi availability, internet, trendy place 3. Close meeting place Factor Close to home/work/school, ability to meet people, quality of coffee not important 4. Intellectual/Non-smoking Factor Non-smokers, usually snack, love to read 5. Familiarity Factor Go to the same bar, do not like trying new places, concerned about quality of coffee 6. Variety/To-go Factor Variety and coffee to go, non traditional Italian coffee, preference for taking coffee alone 7. Traditionality/Addiction Factor Italian coffee preference, addicts

The consumption of Digital Music and its impact on the Music Industry

Factor Analysis § We have taken into consideration questions n° 4, 9, 10 and therefore we have 24 variables §We asked interviewees to give a score from 1 to 9 (1: “I don’t like it” 9: “I love it”) or to use percentages Quest. n. 4: score Quest. n. 9: score Quest. n. 10: % 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Home Car Outside in general Office/University Shops Restaurants Bars/discoteque Record player Cassette player CD player Digital player Car stereo House stereo Radio Mobile phone USE record player USE cassette player USE CD Player USE digital player USE car stereo USE house stereo USE radio USE PC USE mobile phone

Factor Analysis First hypothesis: Number of factors: 9 Extraction: Principal Component Analysis Max number of interaction: 25 Rotation : Varimax

Factor Analysis Ratio between component number ADEQUATE and variable number For a set of 17 variables, the ideal number of components is 4 -5. In this case for a set of 24 variables, we have considered 9 components % global explained variance OK About 68% - the optimal range is 60% - 70% Communalities ADEQUATE The values vary among 0, 456 and 0, 917 We found a problem looking at the rotated component matrix: CORRELATION AMONG COMPONENTS AND ORIGINAL VARIABLES NON OPTIMAL problematic 9 th component

Factor Analysis Number of factors: 8 Second hypothesis: Extraction: Principal Component Analysis Max number of interaction: 25 Rotation : Varimax

Factor Analysis Ratio between component number ADEQUATE and variable number For a set of 17 variables, the ideal number of components is 4 -5. In this case for a set of 24 variables, we have considered 8 components % global explained variance OK About 63% - the optimal range is 60% - 70% Communalities ACCEPTABLE The values vary among 0, 431 and 0, 870

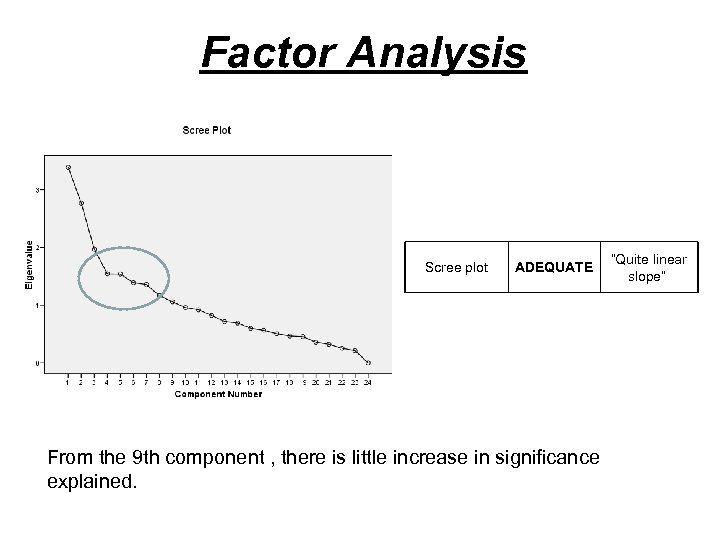Factor Analysis Scree plot ADEQUATE From the 9 th component , there is little increase in significance explained. “Quite linear slope”

Factor Analysis Interpretation 1. Problems with the 9 th component it’s over. 2. We choosed Varimax option to minimize the number of variables that have elevated saturations for each factor WE CHOOSE THE SECOND HYPOTHESIS

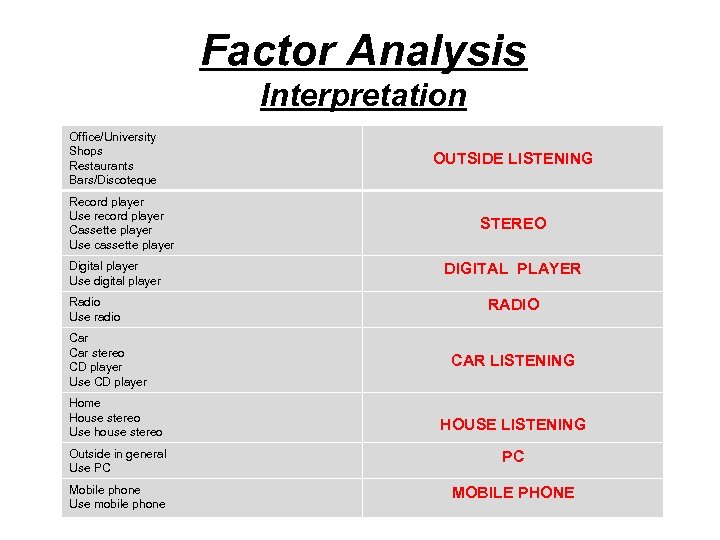Factor Analysis Interpretation Office/University Shops Restaurants Bars/Discoteque Record player Use record player Cassette player Use cassette player Digital player Use digital player Radio Use radio Car stereo CD player Use CD player Home House stereo Use house stereo OUTSIDE LISTENING STEREO DIGITAL PLAYER RADIO CAR LISTENING HOUSE LISTENING Outside in general Use PC PC Mobile phone Use mobile phone MOBILE PHONE