МЕТОД ЗОЛОТОГО СЕЧЕНИЯ(modern).ppt
- Количество слайдов: 16
 МЕТОД ЗОЛОТОГО СЕЧЕНИЯ При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f(x) (или измерений – при проведении эксперимента). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения.
МЕТОД ЗОЛОТОГО СЕЧЕНИЯ При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f(x) (или измерений – при проведении эксперимента). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения.
![Метод золотого сечения состоит в построении последовательности отрезков [a 0, b 0], [a 1, Метод золотого сечения состоит в построении последовательности отрезков [a 0, b 0], [a 1,](https://present5.com/presentation/5942711_1746608/image-2.jpg) Метод золотого сечения состоит в построении последовательности отрезков [a 0, b 0], [a 1, b 1], . . . , стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление значения функции f(x) проводится лишь один раз. Эта точка, называемая золотым сечением, выбирается специальным образом.
Метод золотого сечения состоит в построении последовательности отрезков [a 0, b 0], [a 1, b 1], . . . , стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление значения функции f(x) проводится лишь один раз. Эта точка, называемая золотым сечением, выбирается специальным образом.
![На первом шаге процесса оптимизации внутри отрезка [a 0, b 0] выбираем две внутренние На первом шаге процесса оптимизации внутри отрезка [a 0, b 0] выбираем две внутренние](https://present5.com/presentation/5942711_1746608/image-3.jpg) На первом шаге процесса оптимизации внутри отрезка [a 0, b 0] выбираем две внутренние точки x 1 и x 2 и вычисляем значения целевой функции f(x 1) и f(x 2). Поскольку в данном случае f(x 1)< f(x 2), очевидно что минимум расположен на одном из прилегающих к x 1 отрезков [a 0, x 1] или [x 1, x 2]. Поэтому отрезок [x 2, b 0] можно отбросить, сузив тем самым первоначальный интервал неопределенности. f(x 2) f(x 1) a 0 x 1 x 2 b 0
На первом шаге процесса оптимизации внутри отрезка [a 0, b 0] выбираем две внутренние точки x 1 и x 2 и вычисляем значения целевой функции f(x 1) и f(x 2). Поскольку в данном случае f(x 1)< f(x 2), очевидно что минимум расположен на одном из прилегающих к x 1 отрезков [a 0, x 1] или [x 1, x 2]. Поэтому отрезок [x 2, b 0] можно отбросить, сузив тем самым первоначальный интервал неопределенности. f(x 2) f(x 1) a 0 x 1 x 2 b 0
![Второй шаг проводим на отрезке [a 1, b 1], где a 1=a 0, b Второй шаг проводим на отрезке [a 1, b 1], где a 1=a 0, b](https://present5.com/presentation/5942711_1746608/image-4.jpg) Второй шаг проводим на отрезке [a 1, b 1], где a 1=a 0, b 1= x 2. Нужно снова выбрать две внутренние точки, но одна из них (x 1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку x 3 , вычислить значение f(x 3) и провести сравнение. Поскольку здесь f(x 3)>f(x 1), ясно, что минимум находится на отрезке [x 3, b 1]. Обозначим этот отрезок [a 2, b 2], снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [an, bn] не станет меньше заданной Е. f(x 3) a 1 = a 0 f(x 1) b 1=x 2
Второй шаг проводим на отрезке [a 1, b 1], где a 1=a 0, b 1= x 2. Нужно снова выбрать две внутренние точки, но одна из них (x 1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку x 3 , вычислить значение f(x 3) и провести сравнение. Поскольку здесь f(x 3)>f(x 1), ясно, что минимум находится на отрезке [x 3, b 1]. Обозначим этот отрезок [a 2, b 2], снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [an, bn] не станет меньше заданной Е. f(x 3) a 1 = a 0 f(x 1) b 1=x 2
![Рассмотрим способ размещения внутренних точек на каждом отрезке [ak, bk]. Пусть длина интервала неопределенности Рассмотрим способ размещения внутренних точек на каждом отрезке [ak, bk]. Пусть длина интервала неопределенности](https://present5.com/presentation/5942711_1746608/image-5.jpg) Рассмотрим способ размещения внутренних точек на каждом отрезке [ak, bk]. Пусть длина интервала неопределенности равна L, а точка деления делит его на части L 1, L 2: L 1 > L 2, L= L 1 + L 2. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка: L 1 /L= L 2/ L 1
Рассмотрим способ размещения внутренних точек на каждом отрезке [ak, bk]. Пусть длина интервала неопределенности равна L, а точка деления делит его на части L 1, L 2: L 1 > L 2, L= L 1 + L 2. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка: L 1 /L= L 2/ L 1
 Из этого соотношения можно найти точку деления, определив отношение L 2/L 1. Преобразуем равенство и найдем значение L 2/L 1 : L 1²=L 2*L, L 1²=L 2*(L 1+L 2), L 2²+L 1*L 2 -L 1²=0, (L 2/L 1)²+L 2/L 1 -1=0, L 2/L 1 =(-1+√ 5)/2 и L 2/L 1 =(-1 -√ 5)/2, Поскольку нас интересует только положительное решение, то L 2/L 1 = L 1/L=(-1+√ 5)/2≈0. 618 L 1≈0. 618 L, L 2≈0. 382 L
Из этого соотношения можно найти точку деления, определив отношение L 2/L 1. Преобразуем равенство и найдем значение L 2/L 1 : L 1²=L 2*L, L 1²=L 2*(L 1+L 2), L 2²+L 1*L 2 -L 1²=0, (L 2/L 1)²+L 2/L 1 -1=0, L 2/L 1 =(-1+√ 5)/2 и L 2/L 1 =(-1 -√ 5)/2, Поскольку нас интересует только положительное решение, то L 2/L 1 = L 1/L=(-1+√ 5)/2≈0. 618 L 1≈0. 618 L, L 2≈0. 382 L
 Поскольку заранее неизвестно, в какой последовательности (L 1 и L 2 или L 2 и L 1) делить интервал неопределенности, то рассматривают внутренние точки, соответствующие двум этим способам деления. На рисунке точки деления x 1 и x 2 выбираются с учетом полученных значений для частей отрезка. В данном случае имеем x 1 -a 0=b 0 -x 2= 0. 382 d 0, b 0 -x 1=x 2 -a 0=0. 618 d 0, d 0=b 0 -a 0. a 0 x 1 x 2 b 0
Поскольку заранее неизвестно, в какой последовательности (L 1 и L 2 или L 2 и L 1) делить интервал неопределенности, то рассматривают внутренние точки, соответствующие двум этим способам деления. На рисунке точки деления x 1 и x 2 выбираются с учетом полученных значений для частей отрезка. В данном случае имеем x 1 -a 0=b 0 -x 2= 0. 382 d 0, b 0 -x 1=x 2 -a 0=0. 618 d 0, d 0=b 0 -a 0. a 0 x 1 x 2 b 0
![После первого шага оптимизации получается новый интервал неопределенности – отрезок [a 1, b 1] После первого шага оптимизации получается новый интервал неопределенности – отрезок [a 1, b 1]](https://present5.com/presentation/5942711_1746608/image-8.jpg) После первого шага оптимизации получается новый интервал неопределенности – отрезок [a 1, b 1] a 1=a 0 x 3 x 1 b 1 = x 2 Можно показать, что точка x 1 делит этот отрезок в требуемом отношении, при этом b 1 -x 1=0. 382 d 1, d 1=b 1 -a 1 Проведем преобразования: b 1 -x 1=x 2 -x 1 +d 0 -d 0=x 2 -x 1+ b 0 -a 0 - b 0 +a 0=(b 0 -a 0)-(x 1 a 0)-(b 0 -x 2)=d 0 -0. 382 d 0=0. 236 d 0, d 1=x 2 -a 0=0. 618 d 0, b 1 -x 1=0. 236(d 1/0. 618)=0. 382 d 1
После первого шага оптимизации получается новый интервал неопределенности – отрезок [a 1, b 1] a 1=a 0 x 3 x 1 b 1 = x 2 Можно показать, что точка x 1 делит этот отрезок в требуемом отношении, при этом b 1 -x 1=0. 382 d 1, d 1=b 1 -a 1 Проведем преобразования: b 1 -x 1=x 2 -x 1 +d 0 -d 0=x 2 -x 1+ b 0 -a 0 - b 0 +a 0=(b 0 -a 0)-(x 1 a 0)-(b 0 -x 2)=d 0 -0. 382 d 0=0. 236 d 0, d 1=x 2 -a 0=0. 618 d 0, b 1 -x 1=0. 236(d 1/0. 618)=0. 382 d 1
 Вторая точка деления x 3 выбирается на таком же расстоянии от левой границы отрезка, т. е. x 3 -a 1=0. 382 d 1 И снова интервал неопределенности уменьшается до размера d 2=b 2 -a 2=b 1 -x 3=0. 618 d 1=(0. 618)²d 0 Используя полученные соотношения, можно записать координаты точек деления y и z отрезка [ak, bk] на (k+1)-м шаге оптимизации (y
Вторая точка деления x 3 выбирается на таком же расстоянии от левой границы отрезка, т. е. x 3 -a 1=0. 382 d 1 И снова интервал неопределенности уменьшается до размера d 2=b 2 -a 2=b 1 -x 3=0. 618 d 1=(0. 618)²d 0 Используя полученные соотношения, можно записать координаты точек деления y и z отрезка [ak, bk] на (k+1)-м шаге оптимизации (y
 Процесс оптимизации заканчивается при выполнении условия dk
Процесс оптимизации заканчивается при выполнении условия dk
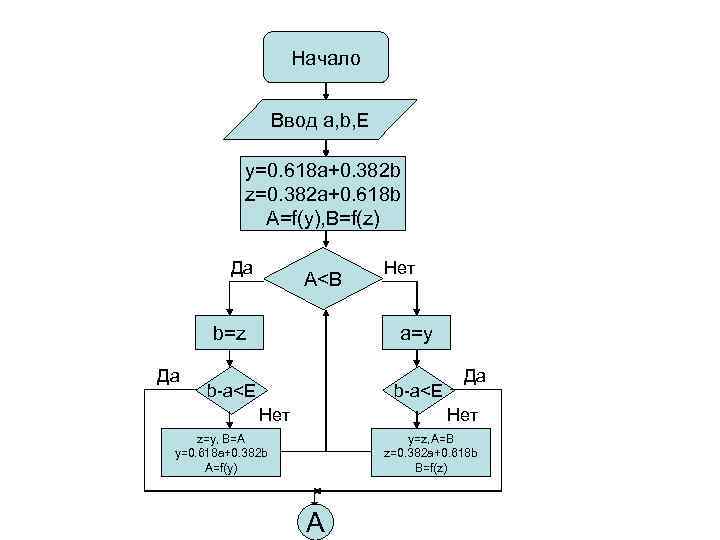 Начало Ввод a, b, E y=0. 618 a+0. 382 b z=0. 382 a+0. 618 b A=f(y), B=f(z) Да A
Начало Ввод a, b, E y=0. 618 a+0. 382 b z=0. 382 a+0. 618 b A=f(y), B=f(z) Да A
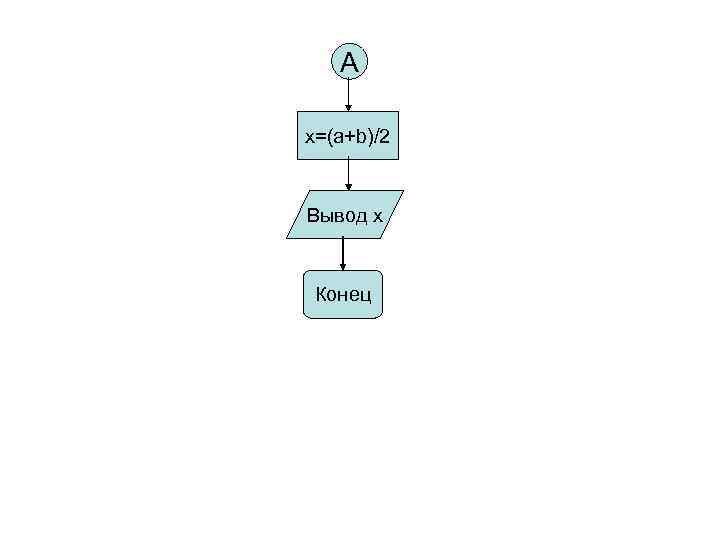 A x=(a+b)/2 Вывод x Конец
A x=(a+b)/2 Вывод x Конец
 Пример Для оценки сопротивления дороги движению автомобиля при скорости V км/ч можно использовать эмпирическую формулу f(V)=242/3*V+1/30*V². Определить скорость, при которой сопротивление будет минимальным. Решение Это задача одномерной оптимизации. Здесь сопротивление f(V)- целевая функция, а V-проектный параметр. Данную задачу легко решить путем нахождения минимума с помощью производной, поскольку данная функция дифференцируемая. f′(V)=2/3+2*V/30=0 V=10 км/ч
Пример Для оценки сопротивления дороги движению автомобиля при скорости V км/ч можно использовать эмпирическую формулу f(V)=242/3*V+1/30*V². Определить скорость, при которой сопротивление будет минимальным. Решение Это задача одномерной оптимизации. Здесь сопротивление f(V)- целевая функция, а V-проектный параметр. Данную задачу легко решить путем нахождения минимума с помощью производной, поскольку данная функция дифференцируемая. f′(V)=2/3+2*V/30=0 V=10 км/ч
 А теперь решим задачу методом золотого сечения. Пусть границы интервала равны: a=5, b=20. Расчеты проводятся в соответствии с блок-схемой с погрешностью E=1 км/ч. Результаты решения приведены в виде таблицы.
А теперь решим задачу методом золотого сечения. Пусть границы интервала равны: a=5, b=20. Расчеты проводятся в соответствии с блок-схемой с погрешностью E=1 км/ч. Результаты решения приведены в виде таблицы.
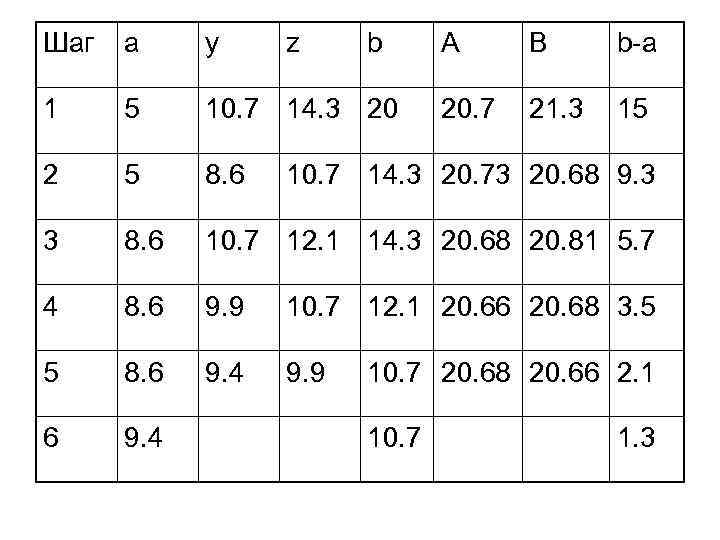 Шаг a y z b A B b-a 1 5 10. 7 14. 3 20 20. 7 21. 3 15 2 5 8. 6 3 8. 6 10. 7 12. 1 14. 3 20. 68 20. 81 5. 7 4 8. 6 9. 9 10. 7 12. 1 20. 66 20. 68 3. 5 5 8. 6 9. 4 9. 9 6 9. 4 10. 7 14. 3 20. 73 20. 68 9. 3 10. 7 20. 68 20. 66 2. 1 10. 7 1. 3
Шаг a y z b A B b-a 1 5 10. 7 14. 3 20 20. 7 21. 3 15 2 5 8. 6 3 8. 6 10. 7 12. 1 14. 3 20. 68 20. 81 5. 7 4 8. 6 9. 9 10. 7 12. 1 20. 66 20. 68 3. 5 5 8. 6 9. 4 9. 9 6 9. 4 10. 7 14. 3 20. 73 20. 68 9. 3 10. 7 20. 68 20. 66 2. 1 10. 7 1. 3
 Решение для первого этапа: y=0. 618*5+0. 382*20≈10. 7 z=0. 382*5+0. 618*20≈14. 3 A=24 -2/3*10. 7+1/30*10. 7²≈20. 7 B=24 -2/3*14. 3+1/30*14. 3²≈21. 3 A
Решение для первого этапа: y=0. 618*5+0. 382*20≈10. 7 z=0. 382*5+0. 618*20≈14. 3 A=24 -2/3*10. 7+1/30*10. 7²≈20. 7 B=24 -2/3*14. 3+1/30*14. 3²≈21. 3 A


